Producto cruzado

Operación matemática sobre vectores en el espacio 3D.

El producto cruzado con respecto a un sistema de coordenadas diestro

En matemáticas , el producto vectorial o producto vectorial (ocasionalmente producto de área dirigido , para enfatizar su significado geométrico) es una operación binaria sobre dos vectores en un espacio vectorial euclidiano orientado tridimensional (nombrado aquí ), y se denota con el símbolo . Dados dos vectores linealmente independientes a y b , el producto cruz, a × b (léase "a cruz b"), es un vector que es perpendicular a a y b , ^[1] y, por tanto, normal al plano que los contiene. Tiene muchas aplicaciones en matemáticas, física , ingeniería y programación informática . No debe confundirse con el producto escalar (producto de proyección). ${\displaystyle E}$ ${\displaystyle \times }$

La magnitud del producto vectorial es igual al área de un paralelogramo con los vectores de los lados; en particular, la magnitud del producto de dos vectores perpendiculares es el producto de sus longitudes. Las unidades del producto cruzado son el producto de las unidades de cada vector. Si dos vectores son paralelos o antiparalelos (es decir, son linealmente dependientes), o si cualquiera de ellos tiene longitud cero, entonces su producto cruzado es cero. ^[2]

El producto cruzado es anticonmutativo (es decir, a × b = − b × a ) y es distributivo sobre la suma, es decir, a × ( b + c ) = a × b + a × c . ^[1] El espacio junto con el producto vectorial es un álgebra sobre los números reales , que no es conmutativo ni asociativo , pero es un álgebra de Lie en el que el producto vectorial es el corchete de Lie . ${\displaystyle E}$

Al igual que el producto escalar, depende de la métrica del espacio euclidiano , pero a diferencia del producto escalar, también depende de la elección de la orientación (o " lateralidad ") del espacio (es por eso que se necesita un espacio orientado). El vector resultante es invariante de la rotación de la base. Debido a la dependencia de la lateralidad , se dice que el producto cruzado es un pseudovector .

En relación con el producto vectorial, el producto exterior de los vectores se puede utilizar en dimensiones arbitrarias (con un resultado bivectorial o de 2 formas ) y es independiente de la orientación del espacio.

El producto se puede generalizar de varias maneras, utilizando la orientación y la estructura métrica, al igual que para el producto cruz tridimensional tradicional, se puede, en n dimensiones, tomar el producto de n − 1 vectores para producir un vector perpendicular a todos ellos. . Pero si el producto se limita a productos binarios no triviales con resultados vectoriales, existe sólo en tres y siete dimensiones. ^{[3] Sin embargo,} el producto cruzado en siete dimensiones tiene propiedades indeseables (por ejemplo, no satisface la identidad de Jacobi ), por lo que no se utiliza en física matemática para representar cantidades como el espacio-tiempo multidimensional . ^[4] (Ver § Generalizaciones a continuación para otras dimensiones).

Definición

Encontrar la dirección del producto vectorial mediante la regla de la mano derecha

El producto cruzado de dos vectores a y b se define sólo en el espacio tridimensional y se denota por a × b . En física y matemáticas aplicadas , la notación de cuña a ∧ b se usa a menudo (junto con el nombre producto vectorial ), ^{[5] [6] [7]} aunque en matemáticas puras dicha notación generalmente se reserva solo para el producto exterior, un abstracción del producto vectorial en n dimensiones.

El producto vectorial a × b se define como un vector c que es perpendicular (ortogonal) tanto a a como a b , con una dirección dada por la regla de la mano derecha ^[1] y una magnitud igual al área del paralelogramo que forman los vectores. durar. ^[2]

El producto cruzado está definido por la fórmula ^{[8] [9]}

${\displaystyle \mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\,\mathbf {n} ,}$

dónde

θ es el ángulo entre a y b en el plano que los contiene (por lo tanto, está entre 0° y 180°),

‖ a ‖ y ‖ b ‖ son las magnitudes de los vectores a y b ,

n es un vector unitario perpendicular al plano que contiene a y b , con dirección tal que el conjunto ordenado ( a , b , n ) está orientado positivamente .

Si los vectores a y b son paralelos (es decir, el ángulo θ entre ellos es 0° o 180°), según la fórmula anterior, el producto cruzado de ayb es el vector cero 0 .

Dirección

El producto vectorial a × b (vertical, en morado) cambia a medida que cambia el ángulo entre los vectores a (azul) y b (rojo). El producto vectorial es siempre ortogonal a ambos vectores y tiene magnitud cero cuando los vectores son paralelos y magnitud máxima ‖ a ‖‖ b ‖ cuando son ortogonales.

La dirección del vector n depende de la orientación elegida del espacio. Convencionalmente, viene dada por la regla de la mano derecha, donde simplemente se apunta el dedo índice de la mano derecha en la dirección de a y el dedo medio en la dirección de b . Entonces, el vector n sale del pulgar (vea la imagen adyacente). Usar esta regla implica que el producto cruz es anticonmutativo ; es decir, b × a = −( a × b ) . Al apuntar primero con el dedo índice hacia b y luego con el dedo medio hacia a , el pulgar se verá forzado en la dirección opuesta, invirtiendo el signo del vector producto.

Como el operador del producto cruzado depende de la orientación del espacio, en general el producto cruzado de dos vectores no es un vector "verdadero", sino un pseudovector . Consulte § Manualidad para obtener más detalles.

Nombres y origen

Según la regla de Sarrus , el determinante de una matriz de 3×3 implica multiplicaciones entre elementos de la matriz identificados por diagonales cruzadas

En 1842, William Rowan Hamilton describió por primera vez el álgebra de cuaterniones y el producto de Hamilton no conmutativo. En particular, cuando se realiza el producto de Hamilton de dos vectores (es decir, cuaterniones puros con parte escalar cero), se obtiene un cuaternión con una parte escalar y una parte vectorial. La parte escalar y vectorial de este producto de Hamilton corresponde al negativo del producto escalar y al producto vectorial de los dos vectores.

En 1881, Josiah Willard Gibbs , ^[10] e independientemente Oliver Heaviside , introdujeron la notación tanto para el producto escalar como para el producto cruz utilizando un punto ( a ⋅ b ) y una "×" ( a × b ), respectivamente, para denotar a ellos. ^[11]

En 1877, para enfatizar el hecho de que el resultado de un producto escalar es un escalar mientras que el resultado de un producto vectorial es un vector , William Kingdon Clifford acuñó los nombres alternativos de producto escalar y producto vectorial para las dos operaciones. ^[11] Estos nombres alternativos todavía se utilizan ampliamente en la literatura.

Tanto la notación cruzada ( a × b ) como el nombre producto cruzado posiblemente se inspiraron en el hecho de que cada componente escalar de a × b se calcula multiplicando componentes no correspondientes de a y b . Por el contrario, un producto escalar a ⋅ b implica multiplicaciones entre los componentes correspondientes de a y b . Como se explica a continuación, el producto cruzado se puede expresar en forma de determinante de una matriz especial de 3 × 3 . Según la regla de Sarrus , se trata de multiplicaciones entre elementos de la matriz identificados por diagonales cruzadas.

Informática

Notación de coordenadas

Vectores de base estándar ( i , j , k , también denotados e ₁ , e ₂ , e ₃ ) y componentes vectoriales de a ( a _x , a _y , a _z , también denotados a ₁ , a ₂ , a ₃ )

Si ( i , j , k ) es una base ortonormal orientada positivamente, los vectores de base satisfacen las siguientes igualdades ^[1]

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {blue}{i}} &\times \mathbf {\color {red}{j}} &&=\mathbf {\color {green}{k}} \\\mathbf {\color {red}{j}} &\times \mathbf {\color {green}{k}} &&=\mathbf {\color {blue}{i}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {blue}{i}} &&=\mathbf {\color {red}{j}} \end{alignedat}}}$

lo que implica, por la anticonmutatividad del producto cruz, que

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}}$

La anticonmutatividad del producto cruz (y la obvia falta de independencia lineal) también implica que

${\displaystyle \mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} =\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} =\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} =\mathbf {0} }$(el vector cero ).

Estas igualdades, junto con la distributividad y la linealidad del producto cruzado (aunque ninguna de ellas se deduce fácilmente de la definición dada anteriormente), son suficientes para determinar el producto cruzado de dos vectores cualesquiera a y b . Cada vector se puede definir como la suma de tres componentes ortogonales paralelos a los vectores de base estándar:

${\displaystyle {\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {\color {blue}{i}} &&+a_{2}\mathbf {\color {red}{j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}}$

Su producto cruzado a × b se puede expandir usando distributividad:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {\color {blue}{i}} +a_{2}\mathbf {\color {red}{j}} +a_{3}\mathbf {\color {green}{k}} )\times (b_{1}\mathbf {\color {blue}{i}} +b_{2}\mathbf {\color {red}{j}} +b_{3}\mathbf {\color {green}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\\&a_{2}b_{1}(\mathbf {\color {red}{j}} \times \mathbf {\color {blue}{i}} )+a_{2}b_{2}(\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} )+a_{2}b_{3}(\mathbf {\color {red}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i}} )+a_{3}b_{2}(\mathbf {\color {green}{k}} \times \mathbf {\color {red}{j}} )+a_{3}b_{3}(\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} )\\\end{aligned}}}$

Esto puede interpretarse como la descomposición de a × b en la suma de nueve productos cruzados más simples que involucran vectores alineados con i , j o ​​k . Cada uno de estos nueve productos cruzados opera sobre dos vectores que son fáciles de manejar ya que son paralelos u ortogonales entre sí. De esta descomposición, utilizando las igualdades antes mencionadas y recogiendo términos similares, obtenemos:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&\quad \ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {\color {green}{k}} -a_{1}b_{3}\mathbf {\color {red}{j}} \\&-a_{2}b_{1}\mathbf {\color {green}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {blue}{i}} \\&+a_{3}b_{1}\mathbf {\color {red}{j}} \ -a_{3}b_{2}\mathbf {\color {blue}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {\color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {green}{k}} \\\end{aligned}}}$

lo que significa que los tres componentes escalares del vector resultante s = s ₁ i + s ₂ j + s ₃ k = a × b son

${\displaystyle {\begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}}$

Usando vectores de columna , podemos representar el mismo resultado de la siguiente manera:

${\displaystyle {\begin{bmatrix}s_{1}\\s_{2}\\s_{3}\end{bmatrix}}={\begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{bmatrix}}}$

Notación matricial

Uso de la regla de Sarrus para encontrar el producto cruzado de a y b

El producto cruzado también se puede expresar como el determinante formal : ^{[nota 1] [1]}

${\displaystyle \mathbf {a\times b} ={\begin{bmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}}$

Este determinante se puede calcular utilizando la regla de Sarrus o la expansión de cofactores . Usando la regla de Sarrus, se expande a

${\displaystyle {\begin{aligned}\mathbf {a\times b} &=(a_{2}b_{3}\mathbf {i} +a_{3}b_{1}\mathbf {j} +a_{1}b_{2}\mathbf {k} )-(a_{3}b_{2}\mathbf {i} +a_{1}b_{3}\mathbf {j} +a_{2}b_{1}\mathbf {k} )\\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} .\end{aligned}}}$

En su lugar , utilizando la expansión de cofactores a lo largo de la primera fila, se expande a ^[12]

${\displaystyle {\begin{aligned}\mathbf {a\times b} &={\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}}\mathbf {k} \\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} -(a_{1}b_{3}-a_{3}b_{1})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} ,\end{aligned}}}$

lo que da directamente los componentes del vector resultante.

Usando tensores Levi-Civita

• En cualquier base, el producto cruzado viene dado por la fórmula tensorial donde es el tensor covariante de Levi-Civita (notamos la posición de los índices). Esto corresponde a la fórmula intrínseca dada aquí. ${\displaystyle a\times b}$ ${\displaystyle E_{ijk}a^{i}b^{j}}$ ${\displaystyle E_{ijk}}$
• En una base ortonormal que tiene la misma orientación que el espacio , viene dada por la fórmula pseudotensorial donde está el símbolo de Levi-Civita (que es un pseudotensor). Ésa es la fórmula utilizada en la física cotidiana, pero sólo funciona para esta elección especial de base. ${\displaystyle a\times b}$ ${\displaystyle \varepsilon _{ijk}a^{i}b^{j}}$ ${\displaystyle \varepsilon _{ijk}}$
• En cualquier base ortonormal, viene dada por la fórmula pseudotensorial donde indica si la base tiene la misma orientación que el espacio o no. ${\displaystyle a\times b}$ ${\displaystyle (-1)^{B}\varepsilon _{ijk}a^{i}b^{j}}$ ${\displaystyle (-1)^{B}=\pm 1}$

Esta última fórmula evita tener que cambiar la orientación del espacio cuando invertimos una base ortonormal.

Propiedades

Significado geométrico

Figura 1. El área de un paralelogramo como magnitud de un producto vectorial

Figura 2. Tres vectores que definen un paralelepípedo

La magnitud del producto vectorial se puede interpretar como el área positiva del paralelogramo que tiene a y b como lados (ver Figura 1): ^[1]

$${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|.}$$

De hecho, también se puede calcular el volumen V de un paralelepípedo que tiene a , b y c como aristas utilizando una combinación de un producto cruz y un producto escalar, llamado triple producto escalar (ver Figura 2):

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}$

Dado que el resultado del triple producto escalar puede ser negativo, el volumen del paralelepípedo viene dado por su valor absoluto:

${\displaystyle V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|.}$

Debido a que la magnitud del producto cruz pasa por el seno del ángulo entre sus argumentos, el producto cruz puede considerarse como una medida de perpendicularidad de la misma manera que el producto escalar es una medida de paralelismo . Dados dos vectores unitarios , su producto vectorial tiene una magnitud de 1 si los dos son perpendiculares y una magnitud de cero si los dos son paralelos. El producto escalar de dos vectores unitarios se comporta de manera opuesta: es cero cuando los vectores unitarios son perpendiculares y 1 si los vectores unitarios son paralelos.

Los vectores unitarios permiten dos identidades convenientes: el producto escalar de dos vectores unitarios produce el coseno (que puede ser positivo o negativo) del ángulo entre los dos vectores unitarios. La magnitud del producto cruzado de los dos vectores unitarios produce el seno (que siempre será positivo).

Propiedades algebraicas

Multiplicación escalar de productos cruzados . Izquierda: Descomposición de b en componentes paralelas y perpendiculares a a . Derecha: Escalado de los componentes perpendiculares mediante un número real positivo r (si es negativo, b y el producto vectorial se invierten).

Distributividad cruzada de productos sobre suma de vectores. Izquierda: Los vectores b y c se resuelven en componentes paralelas y perpendiculares a a . Derecha: Las componentes paralelas desaparecen en el producto vectorial, sólo quedan las componentes perpendiculares que se muestran en el plano perpendicular a a . ^[13]

Los dos productos cruzados triples no equivalentes de tres vectores a , b , c . En cada caso, dos vectores definen un plano, el otro está fuera del plano y se puede dividir en componentes paralelos y perpendiculares al producto cruzado de los vectores que definen el plano. Estos componentes se pueden encontrar mediante proyección y rechazo de vectores . El producto triple está en el plano y gira como se muestra.

Si el producto cruzado de dos vectores es el vector cero (es decir, a × b = 0 ), entonces una o ambas entradas son el vector cero ( a = 0 o b = 0 ) o son paralelas o antiparalelo ( a ∥ b ) de modo que el seno del ángulo entre ellos sea cero ( θ = 0° o θ = 180° y sen  θ = 0 ).

El autoproducto cruzado de un vector es el vector cero:

${\displaystyle \mathbf {a} \times \mathbf {a} =\mathbf {0} .}$

El producto cruzado es anticonmutativo ,

${\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} ),}$

distributivo sobre la suma,

${\displaystyle \mathbf {a} \times (\mathbf {b} +\mathbf {c} )=(\mathbf {a} \times \mathbf {b} )+(\mathbf {a} \times \mathbf {c} ),}$

y compatible con la multiplicación escalar de modo que

${\displaystyle (r\,\mathbf {a} )\times \mathbf {b} =\mathbf {a} \times (r\,\mathbf {b} )=r\,(\mathbf {a} \times \mathbf {b} ).}$

No es asociativo , pero satisface la identidad de Jacobi :

${\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} .}$

La distributividad, la linealidad y la identidad de Jacobi muestran que el espacio vectorial R ³ junto con la suma de vectores y el producto vectorial forma un álgebra de Lie , el álgebra de Lie del grupo ortogonal real en 3 dimensiones, SO(3) . El producto cruzado no obedece a la ley de cancelación ; es decir, a × b = a × c con a ≠ 0 no implica b = c , sino sólo eso:

${\displaystyle {\begin{aligned}\mathbf {0} &=(\mathbf {a} \times \mathbf {b} )-(\mathbf {a} \times \mathbf {c} )\\&=\mathbf {a} \times (\mathbf {b} -\mathbf {c} ).\\\end{aligned}}}$

Este puede ser el caso donde b y c se cancelan, pero además donde a y b − c son paralelos; es decir, están relacionados por un factor de escala t , lo que lleva a:

${\displaystyle \mathbf {c} =\mathbf {b} +t\,\mathbf {a} ,}$

para algún escalar t .

Si, además de a × b = a × c y a ≠ 0 como arriba, se da el caso de que a ⋅ b = a ⋅ c entonces

${\displaystyle {\begin{aligned}\mathbf {a} \times (\mathbf {b} -\mathbf {c} )&=\mathbf {0} \\\mathbf {a} \cdot (\mathbf {b} -\mathbf {c} )&=0,\end{aligned}}}$

Como b − c no puede ser simultáneamente paralelo (para que el producto cruz sea 0 ) y perpendicular (para que el producto escalar sea 0) a a , debe darse el caso de que b y c se cancelen: b = c .

Según la definición geométrica, el producto vectorial es invariante bajo rotaciones adecuadas alrededor del eje definido por a × b . En fórmulas:

${\displaystyle (R\mathbf {a} )\times (R\mathbf {b} )=R(\mathbf {a} \times \mathbf {b} )}$, donde es una matriz de rotación con . ${\displaystyle R}$ ${\displaystyle \det(R)=1}$

De manera más general, el producto cruzado obedece a la siguiente identidad bajo transformaciones matriciales :

${\displaystyle (M\mathbf {a} )\times (M\mathbf {b} )=(\det M)\left(M^{-1}\right)^{\mathrm {T} }(\mathbf {a} \times \mathbf {b} )=\operatorname {cof} M(\mathbf {a} \times \mathbf {b} )}$

donde es una matriz de 3 por 3 y es la transpuesta de la inversa y es la matriz cofactor. Se puede ver fácilmente cómo esta fórmula se reduce a la anterior si es una matriz de rotación. Si se aplica una matriz simétrica de 3 por 3 a un producto cruzado genérico , se cumple la siguiente relación: ${\displaystyle M}$ ${\displaystyle \left(M^{-1}\right)^{\mathrm {T} }}$ ${\displaystyle \operatorname {cof} }$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \mathbf {a} \times \mathbf {b} }$

${\displaystyle M(\mathbf {a} \times \mathbf {b} )=\operatorname {Tr} (M)(\mathbf {a} \times \mathbf {b} )-\mathbf {a} \times M\mathbf {b} +\mathbf {b} \times M\mathbf {a} }$

El producto cruzado de dos vectores se encuentra en el espacio nulo de la matriz de 2 × 3 con los vectores como filas:

${\displaystyle \mathbf {a} \times \mathbf {b} \in NS\left({\begin{bmatrix}\mathbf {a} \\\mathbf {b} \end{bmatrix}}\right).}$

Para la suma de dos productos cruzados, se cumple la siguiente identidad:

${\displaystyle \mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} .}$

Diferenciación

La regla del producto del cálculo diferencial se aplica a cualquier operación bilineal y, por tanto, también al producto cruz:

${\displaystyle {\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}},}$

donde a y b son vectores que dependen de la variable real t .

Triple expansión del producto

El producto cruzado se utiliza en ambas formas del producto triple. El triple producto escalar de tres vectores se define como

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ),}$

Es el volumen con signo del paralelepípedo con aristas a , byc y , como tal, los vectores se pueden usar en cualquier orden que sea una permutación uniforme del orden anterior. Por lo tanto son iguales:

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ),}$

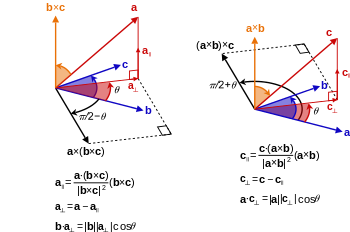
El triple producto vectorial es el producto vectorial de un vector con el resultado de otro producto vectorial, y se relaciona con el producto escalar mediante la siguiente fórmula

${\displaystyle {\begin{aligned}\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )\\(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-\mathbf {a} (\mathbf {b} \cdot \mathbf {c} )\end{aligned}}}$

El mnemónico "BAC menos CAB" se utiliza para recordar el orden de los vectores en el miembro de la derecha. Esta fórmula se utiliza en física para simplificar los cálculos vectoriales. Un caso especial, relacionado con gradientes y útil en cálculo vectorial , es

${\displaystyle {\begin{aligned}\nabla \times (\nabla \times \mathbf {f} )&=\nabla (\nabla \cdot \mathbf {f} )-(\nabla \cdot \nabla )\mathbf {f} \\&=\nabla (\nabla \cdot \mathbf {f} )-\nabla ^{2}\mathbf {f} ,\\\end{aligned}}}$

donde ∇ ² es el operador vectorial laplaciano .

Otras identidades relacionan el producto cruzado con el triple producto escalar:

${\displaystyle {\begin{aligned}(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )&=(\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ))\mathbf {a} \\(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )&=\mathbf {b} ^{\mathrm {T} }\left(\left(\mathbf {c} ^{\mathrm {T} }\mathbf {a} \right)I-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\&=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )\end{aligned}}}$

donde I es la matriz identidad.

Formulación alternativa

El producto cruzado y el producto escalar están relacionados por:

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

El lado derecho es el determinante de Gram de a y b , el cuadrado del área del paralelogramo definido por los vectores. Esta condición determina la magnitud del producto cruzado. Es decir, dado que el producto escalar se define, en términos del ángulo θ entre los dos vectores, como:

${\displaystyle \mathbf {a\cdot b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,}$

La relación dada anteriormente se puede reescribir de la siguiente manera:

${\displaystyle \left\|\mathbf {a\times b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}\left(1-\cos ^{2}\theta \right).}$

Invocando la identidad trigonométrica pitagórica se obtiene:

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|,}$

que es la magnitud del producto cruzado expresado en términos de θ , igual al área del paralelogramo definido por a y b (ver definición arriba).

La combinación de este requisito y la propiedad de que el producto cruz sea ortogonal a sus constituyentes a y b proporciona una definición alternativa del producto cruz. ^[14]

Producto cruzado inverso

Para el producto cruzado a × b = c , hay varios vectores b que dan el mismo valor de c . Como resultado, no es posible reordenar esta ecuación para obtener una solución única para b en términos de a y c . Sin embargo, es posible encontrar una familia de soluciones para b , que son

${\displaystyle \mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+t\mathbf {a} ,}$

donde t es una constante arbitraria.

Esto se puede derivar usando la expansión del triple producto:

${\displaystyle \mathbf {c} \times \mathbf {a} =(\mathbf {a} \times \mathbf {b} )\times \mathbf {a} =\left\|\mathbf {a} \right\|^{2}\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {a} }$

Reorganizar para resolver b para dar

${\displaystyle \mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|^{2}}}\mathbf {a} }$

El coeficiente del último término se puede simplificar a solo la constante arbitraria t para obtener el resultado que se muestra arriba.

La identidad de Lagrange

La relación

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|^{2}\equiv \det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{bmatrix}}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}}$

se puede comparar con otra relación que involucra el lado derecho, a saber, la identidad de Lagrange expresada como ^[15]

${\displaystyle \sum _{1\leq i<j\leq n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a\cdot b} )^{2},}$

donde a y b pueden ser vectores n -dimensionales. Esto también muestra que la forma de volumen de Riemann para superficies es exactamente el elemento de superficie del cálculo vectorial. En el caso donde n = 3 , la combinación de estas dos ecuaciones da como resultado la expresión de la magnitud del producto cruzado en términos de sus componentes: ^[16]

${\displaystyle {\begin{aligned}\|\mathbf {a} \times \mathbf {b} \|^{2}&\equiv \sum _{1\leq i<j\leq 3}(a_{i}b_{j}-a_{j}b_{i})^{2}\\&\equiv (a_{1}b_{2}-b_{1}a_{2})^{2}+(a_{2}b_{3}-a_{3}b_{2})^{2}+(a_{3}b_{1}-a_{1}b_{3})^{2}.\end{aligned}}}$

El mismo resultado se encuentra directamente usando los componentes del producto cruzado encontrado en

${\displaystyle \mathbf {a} \times \mathbf {b} \equiv \det {\begin{bmatrix}{\hat {\mathbf {i} }}&{\hat {\mathbf {j} }}&{\hat {\mathbf {k} }}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}.}$

En R ³ , la ecuación de Lagrange es un caso especial de multiplicatividad | VW | = | v || w | de la norma en el álgebra de cuaterniones .

Es un caso especial de otra fórmula, también llamada a veces identidad de Lagrange, que es el caso tridimensional de la identidad Binet-Cauchy : ^{[17] [18]}

${\displaystyle (\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )\equiv (\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} ).}$

Si a = c y b = d , esto se simplifica a la fórmula anterior.

Generadores infinitesimales de rotaciones.

El producto cruz describe convenientemente los generadores infinitesimales de rotaciones en R ³ . Específicamente, si n es un vector unitario en R ³ y R ( φ ,  n ) denota una rotación alrededor del eje que pasa por el origen especificado por n , con un ángulo φ (medido en radianes, en sentido antihorario visto desde la punta de n ), entonces

${\displaystyle \left.{d \over d\phi }\right|_{\phi =0}R(\phi ,{\boldsymbol {n}}){\boldsymbol {x}}={\boldsymbol {n}}\times {\boldsymbol {x}}}$

para cada vector x en R ³ . Por tanto, el producto cruz con n describe el generador infinitesimal de las rotaciones alrededor de n . Estos generadores infinitesimales forman el álgebra de Lie so (3) del grupo de rotación SO(3) , y obtenemos el resultado de que el álgebra de Lie R ³ con producto cruzado es isomorfo al álgebra de Lie so (3).

Formas alternativas de calcular

Conversión a multiplicación de matrices

El producto vectorial vectorial también se puede expresar como el producto de una matriz simétrica sesgada y un vector: ^[17]

$${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} &={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf {b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_{3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}},\end{aligned}}}$$

^Tde transposicióna_×

$${\displaystyle [\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.}$$

Las columnas [ a ] _×,i de la matriz simétrica sesgada para un vector a también se pueden obtener calculando el producto cruzado con vectores unitarios . Eso es,

$${\displaystyle [\mathbf {a} ]_{\times ,i}=\mathbf {a} \times \mathbf {{\hat {e}}_{i}} ,\;i\in \{1,2,3\}}$$

$${\displaystyle [\mathbf {a} ]_{\times }=\sum _{i=1}^{3}\left(\mathbf {a} \times \mathbf {{\hat {e}}_{i}} \right)\otimes \mathbf {{\hat {e}}_{i}} ,}$$

del producto externo ? ${\displaystyle \otimes }$

Además, si a se expresa como un producto cruzado:

$${\displaystyle \mathbf {a} =\mathbf {c} \times \mathbf {d} }$$

$${\displaystyle [\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }.}$$

Prueba por sustitución

La evaluación del producto cruzado da

$${\displaystyle \mathbf {a} =\mathbf {c} \times \mathbf {d} ={\begin{pmatrix}c_{2}d_{3}-c_{3}d_{2}\\c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}\end{pmatrix}}}$$

Por lo tanto, el lado izquierdo es igual

$${\displaystyle [\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}$$

Ahora, para el lado derecho,

$${\displaystyle \mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{1}d_{2}&c_{1}d_{3}\\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\\c_{3}d_{1}&c_{3}d_{2}&c_{3}d_{3}\end{bmatrix}}}$$

Y su transposición es

$${\displaystyle \mathbf {d} \mathbf {c} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{2}d_{1}&c_{3}d_{1}\\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\\c_{1}d_{3}&c_{2}d_{3}&c_{3}d_{3}\end{bmatrix}}}$$

La evaluación del lado derecho da

$${\displaystyle \mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}$$

La comparación muestra que el lado izquierdo es igual al lado derecho.

Este resultado se puede generalizar a dimensiones superiores utilizando álgebra geométrica . En particular, en cualquier dimensión, los bivectores se pueden identificar con matrices simétricas sesgadas, por lo que el producto entre una matriz simétrica sesgada y un vector es equivalente a la parte de grado 1 del producto de un bivector y un vector. ^[19] En tres dimensiones, los bivectores son duales con respecto a los vectores, por lo que el producto es equivalente al producto cruzado, con el bivector en lugar de su vector dual. En dimensiones superiores aún se puede calcular el producto, pero los bivectores tienen más grados de libertad y no son equivalentes a los vectores. ^[19]

También suele ser mucho más fácil trabajar con esta notación, por ejemplo, en geometría epipolar .

De las propiedades generales del producto cruz se sigue inmediatamente que

$${\displaystyle [\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0} }$$

$${\displaystyle \mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0} }$$

a_​​×

$${\displaystyle \mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.}$$

La expansión del triple producto mencionada anteriormente (regla bac-cab) se puede demostrar fácilmente utilizando esta notación.

Como se mencionó anteriormente, el álgebra de Lie R ³ con producto cruzado es isomorfo al álgebra de Lie so(3) , cuyos elementos pueden identificarse con las matrices simétricas sesgadas de 3×3. El mapa a → [ a ] _​​× proporciona un isomorfismo entre R ³ y so(3) . Según este mapa, el producto cruzado de 3 vectores corresponde al conmutador de matrices simétricas sesgadas de 3x3.

Notación de índice para tensores

El producto cruzado también se puede definir en términos del tensor de Levi-Civita E _ijk y un producto escalar η ^mi , que son útiles para convertir notación vectorial para aplicaciones de tensor:

${\displaystyle \mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\eta ^{mi}E_{ijk}a^{j}b^{k}}$

donde los índices corresponden a componentes vectoriales. Esta caracterización del producto vectorial a menudo se expresa de manera más compacta utilizando la convención de suma de Einstein como ${\displaystyle i,j,k}$

${\displaystyle \mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\eta ^{mi}E_{ijk}a^{j}b^{k}}$

en el que los índices repetidos se suman entre los valores 1 a 3.

En una base ortonormal orientada positivamente η ^mi = δ ^mi (el delta de Kronecker ) y (el símbolo de Levi-Civita ). En ese caso, esta representación es otra forma de representación simétrica sesgada del producto vectorial: ${\displaystyle E_{ijk}=\varepsilon _{ijk}}$

${\displaystyle [\varepsilon _{ijk}a^{j}]=[\mathbf {a} ]_{\times }.}$

En mecánica clásica : representar el producto vectorial mediante el símbolo de Levi-Civita puede hacer que las simetrías mecánicas sean obvias cuando los sistemas físicos son isotrópicos . (Un ejemplo: considere una partícula en un potencial de la Ley de Hooke en tres espacios, libre para oscilar en tres dimensiones; ninguna de estas dimensiones es "especial" en ningún sentido, por lo que las simetrías residen en el momento angular representado por el producto cruzado, que quedan claros en la declaración de Levi-Civita antes mencionada). ^{[ cita necesaria ]}

Mnemotécnico

Mnemónico para calcular un producto cruzado en forma vectorial

La palabra "xyzzy" se puede utilizar para recordar la definición del producto cruzado.

Si

${\displaystyle \mathbf {a} =\mathbf {b} \times \mathbf {c} }$

dónde:

${\displaystyle \mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}},\ \mathbf {b} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}},\ \mathbf {c} ={\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}}$

entonces:

${\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}}$

${\displaystyle a_{y}=b_{z}c_{x}-b_{x}c_{z}}$

${\displaystyle a_{z}=b_{x}c_{y}-b_{y}c_{x}.}$

La segunda y tercera ecuaciones se pueden obtener a partir de la primera simplemente rotando verticalmente los subíndices, x → y → z → x . El problema, por supuesto, es cómo recordar la primera ecuación, y hay dos opciones disponibles para este propósito: recordar las dos diagonales relevantes del esquema de Sarrus (las que contienen i ), o recordar la secuencia xyzzy.

Dado que la primera diagonal en el esquema de Sarrus es solo la diagonal principal de la matriz de 3 × 3 antes mencionada, las primeras tres letras de la palabra xyzzy se pueden recordar muy fácilmente.

visualización cruzada

De manera similar al dispositivo mnemotécnico anterior, se puede visualizar una "cruz" o X entre los dos vectores de la ecuación. Esto puede resultar útil para recordar la fórmula correcta de productos cruzados.

Si

${\displaystyle \mathbf {a} =\mathbf {b} \times \mathbf {c} }$

entonces:

${\displaystyle \mathbf {a} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}.}$

Si queremos obtener la fórmula para, simplemente eliminamos y de la fórmula y eliminamos los dos componentes siguientes: ${\displaystyle a_{x}}$ ${\displaystyle b_{x}}$ ${\displaystyle c_{x}}$

${\displaystyle a_{x}={\begin{bmatrix}b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{y}\\c_{z}\end{bmatrix}}.}$

Al hacer esto para los dos elementos siguientes, se debe "envolver" la matriz de modo que después del componente z venga el componente x. Para mayor claridad, al realizar esta operación para , los siguientes dos componentes deben ser z y x (en ese orden). Mientras que para los dos siguientes componentes se deben tomar como x e y. ${\displaystyle a_{y}}$ ${\displaystyle a_{y}}$ ${\displaystyle a_{z}}$

${\displaystyle a_{y}={\begin{bmatrix}b_{z}\\b_{x}\end{bmatrix}}\times {\begin{bmatrix}c_{z}\\c_{x}\end{bmatrix}},\ a_{z}={\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\end{bmatrix}}}$

Entonces , si visualizamos el operador de cruz apuntando desde un elemento de la izquierda a un elemento de la derecha, podemos tomar el primer elemento de la izquierda y simplemente multiplicarlo por el elemento al que apunta la cruz en la matriz de la derecha. . Luego restamos el siguiente elemento hacia abajo a la izquierda, multiplicado por el elemento al que apunta la cruz aquí también. Esto da como resultado nuestra fórmula: ${\displaystyle a_{x}}$ ${\displaystyle a_{x}}$

${\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}.}$

Podemos hacer esto de la misma manera para y para construir sus fórmulas asociadas. ${\displaystyle a_{y}}$ ${\displaystyle a_{z}}$

Aplicaciones

El producto cruzado tiene aplicaciones en diversos contextos. Por ejemplo, se utiliza en geometría computacional, física e ingeniería. A continuación se incluye una lista no exhaustiva de ejemplos.

Geometría Computacional

El producto vectorial aparece en el cálculo de la distancia de dos líneas oblicuas (líneas que no están en el mismo plano) entre sí en un espacio tridimensional.

El producto cruzado se puede utilizar para calcular la normal de un triángulo o polígono, una operación que se realiza con frecuencia en gráficos por computadora . Por ejemplo, la curvatura de un polígono (en sentido horario o antihorario) alrededor de un punto dentro del polígono se puede calcular triangulando el polígono (como los radios de una rueda) y sumando los ángulos (entre los radios) usando el producto vectorial para realizar un seguimiento de los signo de cada ángulo.

En geometría computacional del plano , el producto cruz se utiliza para determinar el signo del ángulo agudo definido por tres puntos y . Corresponde a la dirección (hacia arriba o hacia abajo) del producto cruzado de los dos vectores coplanares definidos por los dos pares de puntos y . El signo del ángulo agudo es el signo de la expresión. ${\displaystyle p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})}$ ${\displaystyle p_{3}=(x_{3},y_{3})}$ ${\displaystyle (p_{1},p_{2})}$ ${\displaystyle (p_{1},p_{3})}$

${\displaystyle P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),}$

que es la longitud con signo del producto cruzado de los dos vectores.

En el sistema de coordenadas "diestros", si el resultado es 0, los puntos son colineales ; si es positivo, los tres puntos constituyen un ángulo de rotación positivo alrededor de a , en caso contrario, un ángulo negativo. Desde otro punto de vista, el signo de indica si se encuentra a la izquierda o a la derecha de la línea. ${\displaystyle p_{1}}$ ${\displaystyle p_{2}}$ ${\displaystyle p_{3}}$ ${\displaystyle P}$ ${\displaystyle p_{3}}$ ${\displaystyle p_{1},p_{2}.}$

El producto vectorial se utiliza para calcular el volumen de un poliedro como un tetraedro o un paralelepípedo .

Momento angular y par

El momento angular L de una partícula con respecto a un origen dado se define como:

${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} ,}$

donde r es el vector de posición de la partícula con respecto al origen, p es el momento lineal de la partícula.

De la misma manera, el momento M de una fuerza F _B aplicada en el punto B alrededor del punto A viene dado por:

${\displaystyle \mathbf {M} _{\mathrm {A} }=\mathbf {r} _{\mathrm {AB} }\times \mathbf {F} _{\mathrm {B} }\,}$

En mecánica el momento de una fuerza también se llama torque y se escribe como ${\displaystyle \mathbf {\tau } }$

Dado que la posición r , el momento lineal p y la fuerza F son todos vectores verdaderos , tanto el momento angular L como el momento de una fuerza M son pseudovectores o vectores axiales .

Cuerpo rígido

El producto cruz aparece frecuentemente en la descripción de movimientos rígidos. Dos puntos P y Q de un cuerpo rígido se pueden relacionar mediante:

${\displaystyle \mathbf {v} _{P}-\mathbf {v} _{Q}={\boldsymbol {\omega }}\times \left(\mathbf {r} _{P}-\mathbf {r} _{Q}\right)\,}$

donde es la posición del punto, es su velocidad y es la velocidad angular del cuerpo . ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle {\boldsymbol {\omega }}}$

Dado que la posición y la velocidad son vectores verdaderos , la velocidad angular es un pseudovector o vector axial . ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle {\boldsymbol {\omega }}}$

fuerza de lorentz

El producto cruz se utiliza para describir la fuerza de Lorentz experimentada por una carga eléctrica en movimiento q _e :

${\displaystyle \mathbf {F} =q_{e}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$

Dado que la velocidad v , la fuerza F y el campo eléctrico E son todos vectores verdaderos , el campo magnético B es un pseudovector .

Otro

En cálculo vectorial , el producto cruzado se utiliza para definir la fórmula para el operador vectorial curl .

El truco de reescribir un producto cruzado en términos de una multiplicación de matrices aparece frecuentemente en geometría epipolar y de múltiples vistas, en particular cuando se derivan restricciones coincidentes.

Como producto externo

El producto cruzado en relación con el producto exterior. En rojo están el vector unitario ortogonal y el bivector unitario "paralelo".

El producto cruzado se puede definir en términos del producto exterior. Se puede generalizar a un producto externo en otras dimensiones que no sean tres. ^[20] Esta generalización permite una interpretación geométrica natural del producto vectorial. En álgebra exterior, el producto exterior de dos vectores es un bivector. Un bivector es un elemento plano orientado, de la misma manera que un vector es un elemento lineal orientado. Dados dos vectores a y b , se puede ver el bivector a ∧ b como el paralelogramo orientado abarcado por a y b . Luego, el producto vectorial se obtiene tomando la estrella de Hodge del bivector a ∧ b , asignando 2 vectores a vectores:

${\displaystyle a\times b=\star (a\wedge b).}$

Esto puede considerarse como el elemento multidimensional orientado "perpendicular" al bivector. En un espacio d- dimensional, la estrella de Hodge toma un k -vector a un ( d – k ) -vector; por tanto, sólo en d = 3 dimensiones el resultado es un elemento de dimensión uno (3–2 = 1), es decir, un vector. Por ejemplo, en d = 4 dimensiones, el producto cruzado de dos vectores tiene dimensión 4–2 = 2, lo que da un bivector. Por tanto, sólo en tres dimensiones el producto vectorial define una estructura algebraica para multiplicar vectores.

lateralidad

Consistencia

Cuando las leyes físicas se escriben como ecuaciones, es posible realizar una elección arbitraria del sistema de coordenadas, incluida la lateralidad. Se debe tener cuidado de no escribir nunca una ecuación en la que los dos lados no se comporten de la misma manera en todas las transformaciones que deban considerarse. Por ejemplo, si un lado de la ecuación es producto cruzado de dos vectores polares , hay que tener en cuenta que el resultado es un vector axial . Por lo tanto, por coherencia, el otro lado también debe ser un vector axial. ^{[ cita necesaria ]} De manera más general, el resultado de un producto cruzado puede ser un vector polar o un vector axial, dependiendo del tipo de sus operandos (vectores polares o vectores axiales). Es decir, los vectores polares y los vectores axiales están interrelacionados de las siguientes maneras bajo la aplicación del producto vectorial:

• vector polar × vector polar = vector axial
• vector axial × vector axial = vector axial
• vector polar × vector axial = vector polar
• vector axial × vector polar = vector polar

o simbólicamente

• polar × polar = axial
• axial × axial = axial
• polar × axial = polar
• axial × polar = polar

Debido a que el producto vectorial también puede ser un vector polar, es posible que no cambie de dirección con una transformación de imagen especular. Esto sucede, según las relaciones anteriores, si uno de los operandos es un vector polar y el otro es un vector axial (por ejemplo, el producto cruzado de dos vectores polares). Por ejemplo, un producto triple vectorial que involucra tres vectores polares es un vector polar.

Es posible un enfoque sin uso de las manos utilizando álgebra exterior.

La paradoja de la base ortonormal.

Sea ( i , j , k ) una base ortonormal. Los vectores i , j y k no dependen de la orientación del espacio. Incluso pueden definirse en ausencia de orientación alguna. Por tanto, no pueden ser vectores axiales. Pero si i y j son vectores polares, entonces k es un vector axial para i × j = k o j × i = k . Esto es una paradoja.

"Axial" y "polar" son calificadores físicos de vectores físicos ; es decir, vectores que representan cantidades físicas como la velocidad o el campo magnético. Los vectores i , j y k son vectores matemáticos, ni axiales ni polares. En matemáticas, el producto cruzado de dos vectores es un vector. No hay contradicción.

Generalizaciones

Hay varias formas de generalizar el producto cruzado a dimensiones superiores.

álgebra de mentiras

El producto cruz puede verse como uno de los productos de Lie más simples y, por lo tanto, se generaliza mediante álgebras de Lie , que se axiomatizan como productos binarios que satisfacen los axiomas de multilinealidad, simetría sesgada y la identidad de Jacobi. Existen muchas álgebras de Lie y su estudio es un campo importante de las matemáticas, llamado teoría de Lie .

Por ejemplo, el álgebra de Heisenberg da otra estructura de álgebra de Lie sobre la base del producto: ${\displaystyle \mathbf {R} ^{3}.}$ ${\displaystyle \{x,y,z\},}$ ${\displaystyle [x,y]=z,[x,z]=[y,z]=0.}$

Cuaterniones

El producto cruzado también se puede describir en términos de cuaterniones . En general, si un vector [ a ₁ , a ₂ , a ₃ ] se representa como el cuaternión a ₁ i + a ₂ j + a ₃ k , el producto cruzado de dos vectores se puede obtener tomando su producto como cuaterniones y eliminando la parte real del resultado. La parte real será el negativo del producto escalar de los dos vectores.

Octoniones

Se puede obtener un producto vectorial para vectores de 7 dimensiones de la misma manera usando octoniones en lugar de cuaterniones. La no existencia de productos cruzados no triviales con valores vectoriales de dos vectores en otras dimensiones está relacionada con el resultado del teorema de Hurwitz de que las únicas álgebras de división normadas son las que tienen dimensiones 1, 2, 4 y 8.

Producto exterior

En dimensión general, no existe un análogo directo del producto cruzado binario que produzca específicamente un vector. Sin embargo, existe el producto exterior, que tiene propiedades similares, excepto que el producto exterior de dos vectores ahora es un vector 2 en lugar de un vector ordinario. Como se mencionó anteriormente, el producto vectorial se puede interpretar como el producto exterior en tres dimensiones utilizando el operador estrella de Hodge para asignar 2 vectores a vectores. El dual de Hodge del producto exterior produce un ( n − 2 ) -vector, que es una generalización natural del producto vectorial en cualquier número de dimensiones.

El producto exterior y el producto escalar se pueden combinar (mediante suma) para formar el producto geométrico en álgebra geométrica.

Producto externo

Como se mencionó anteriormente, el producto cruz se puede interpretar en tres dimensiones como el dual de Hodge del producto exterior. En cualquier n dimensiones finitas, el dual de Hodge del producto exterior de n − 1 vectores es un vector. Entonces, en lugar de una operación binaria, en dimensiones finitas arbitrarias, el producto cruz se generaliza como el dual de Hodge del producto exterior de algunos n − 1 vectores dados. Esta generalización se llama producto externo . ^[21]

Producto conmutador

Interpretar el espacio vectorial tridimensional del álgebra como la subálgebra de 2 vectores (no el de 1 vector) del álgebra geométrica tridimensional, donde , y , el producto cruzado corresponde exactamente al producto del conmutador en álgebra geométrica y ambos Utiliza el mismo símbolo . El producto del conmutador se define para 2 vectores y en álgebra geométrica como: ${\displaystyle \mathbf {i} =\mathbf {e_{2}} \mathbf {e_{3}} }$ ${\displaystyle \mathbf {j} =\mathbf {e_{1}} \mathbf {e_{3}} }$ ${\displaystyle \mathbf {k} =\mathbf {e_{1}} \mathbf {e_{2}} }$ ${\displaystyle \times }$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A\times B={\tfrac {1}{2}}(AB-BA),}$

¿ Dónde está el producto geométrico? ^[22] ${\displaystyle AB}$

El producto del conmutador podría generalizarse a multivectores arbitrarios en tres dimensiones, lo que da como resultado un multivector que consta únicamente de elementos de grados 1 (1-vectores/vectores verdaderos) y 2 (2-vectores/pseudovectores). Mientras que el producto del conmutador de dos vectores 1 es de hecho el mismo que el producto exterior y produce un vector 2, el conmutador de un vector 1 y un vector 2 produce un vector verdadero, correspondiente a las contracciones izquierda y derecha en álgebra geométrica. El producto del conmutador de dos 2 vectores no tiene un producto equivalente correspondiente, por lo que el producto del conmutador se define en primer lugar para 2 vectores. Además, el producto triple del conmutador de tres 2 vectores es el mismo que el producto triple del vector de los mismos tres pseudovectores en álgebra vectorial. Sin embargo, el producto triple del conmutador de tres vectores 1 en álgebra geométrica es, en cambio, el negativo del producto triple vectorial de los mismos tres vectores verdaderos en álgebra vectorial.

Las generalizaciones a dimensiones superiores las proporciona el mismo producto conmutador de 2 vectores en álgebras geométricas de dimensiones superiores, pero los 2 vectores ya no son pseudovectores. Así como el producto conmutador/producto cruzado de 2 vectores en tres dimensiones corresponde al álgebra de Lie más simple, las subálgebras de 2 vectores del álgebra geométrica de dimensiones superiores equipadas con el producto conmutador también corresponden a las álgebras de Lie. ^[23] También como en tres dimensiones, el producto del conmutador podría generalizarse aún más a multivectores arbitrarios.

Álgebra multilineal

En el contexto del álgebra multilineal , el producto vectorial puede verse como el tensor (1,2) (un tensor mixto , específicamente un mapa bilineal ) obtenido de la forma de volumen tridimensional , ^{[nota 2]} a (0,3 )-tensor, elevando un índice .

En detalle, la forma de volumen tridimensional define un producto tomando el determinante de la matriz dada por estos 3 vectores. Por dualidad , esto es equivalente a una función (fijar dos entradas cualesquiera da una función evaluando la tercera entrada) y en presencia de un producto interno (como el producto escalar; más generalmente, una forma bilineal no degenerada), tenemos un isomorfismo y, por lo tanto, esto produce un mapa que es el producto cruzado: un tensor (0,3) (3 entradas vectoriales, salida escalar) se ha transformado en un tensor (1,2) (2 entradas vectoriales, 1 salida vectorial) "levantando un índice". ${\displaystyle V\times V\times V\to \mathbf {R} ,}$ ${\displaystyle V\times V\to V^{*},}$ ${\displaystyle V\to \mathbf {R} }$ ${\displaystyle V\to V^{*},}$ ${\displaystyle V\times V\to V,}$

Traduciendo el álgebra anterior a geometría, la función "volumen del paralelepípedo definido por " (donde los dos primeros vectores son fijos y el último es una entrada), que define una función , se puede representar únicamente como el producto escalar con un vector: este vector es el producto cruzado. Desde esta perspectiva, el producto cruzado está definido por el triple producto escalar , ${\displaystyle (a,b,-)}$ ${\displaystyle V\to \mathbf {R} }$ ${\displaystyle a\times b.}$ ${\displaystyle \mathrm {Vol} (a,b,c)=(a\times b)\cdot c.}$

De la misma manera, en dimensiones superiores se pueden definir productos cruzados generalizados elevando índices de la forma de volumen n -dimensional, que es un tensor. Las generalizaciones más directas del producto cruzado son definir: ${\displaystyle (0,n)}$

• un -tensor, que toma como vectores de entrada y da como salida 1 vector, un producto con valor vectorial -ario, o ${\displaystyle (1,n-1)}$ ${\displaystyle n-1}$ ${\displaystyle (n-1)}$
• un -tensor, que toma como entrada 2 vectores y da como salida un tensor sesgado-simétrico de rango n - 2 - un producto binario con rango n - 2 valores de tensor. También se pueden definir -tensores para otros k . ${\displaystyle (n-2,2)}$ ${\displaystyle (k,n-k)}$

Todos estos productos son multilineales y asimétricos, y pueden definirse en términos del determinante y la paridad .

El producto ario se puede describir de la siguiente manera: los vectores dados definen su producto cruzado generalizado como: ${\displaystyle (n-1)}$ ${\displaystyle n-1}$ ${\displaystyle v_{1},\dots ,v_{n-1}}$ ${\displaystyle \mathbf {R} ^{n},}$ ${\displaystyle v_{n}=v_{1}\times \cdots \times v_{n-1}}$

• perpendicular al hiperplano definido por el ${\displaystyle v_{i},}$
• magnitud es el volumen del paralelotopo definido por el cual se puede calcular como el determinante de Gram del ${\displaystyle v_{i},}$ ${\displaystyle v_{i},}$
• orientado de modo que esté orientado positivamente. ${\displaystyle v_{1},\dots ,v_{n}}$

Este es el único producto alterno multilineal que se evalúa como , etc. para permutaciones cíclicas de índices. ${\displaystyle e_{1}\times \cdots \times e_{n-1}=e_{n}}$ ${\displaystyle e_{2}\times \cdots \times e_{n}=e_{1},}$

En coordenadas, se puede dar una fórmula para este análogo ario del producto vectorial en R ⁿ mediante: ${\displaystyle (n-1)}$

${\displaystyle \bigwedge _{i=0}^{n-1}\mathbf {v} _{i}={\begin{vmatrix}v_{1}{}^{1}&\cdots &v_{1}{}^{n}\\\vdots &\ddots &\vdots \\v_{n-1}{}^{1}&\cdots &v_{n-1}{}^{n}\\\mathbf {e} _{1}&\cdots &\mathbf {e} _{n}\end{vmatrix}}.}$

Esta fórmula es idéntica en estructura a la fórmula determinante para el producto cruzado normal en R ³ excepto que la fila de vectores base es la última fila del determinante en lugar de la primera. La razón de esto es asegurar que los vectores ordenados ( v ₁ , ..., v _{n −1} , Λ^{norte –1}
_{yo = 0}vi ₎ tienen una orientación positiva con respecto a ( e ₁ , ..., e _n ). Si n es impar, esta modificación deja el valor sin cambios, por lo que esta convención concuerda con la definición normal del producto binario. Sin embargo, en el caso de que n sea par, se debe mantener la distinción. Esta forma -aria disfruta de muchas de las mismas propiedades que el producto vectorial vectorial: es alternante y lineal en sus argumentos, es perpendicular a cada argumento y su magnitud da el hipervolumen de la región delimitada por los argumentos. Y al igual que el producto vectorial vectorial, se puede definir de forma independiente de las coordenadas como el dual de Hodge del producto de cuña de los argumentos. Además, el producto satisface la identidad de Filippov, ${\displaystyle (n-1)}$ ${\displaystyle [v_{1},\ldots ,v_{n}]:=\bigwedge _{i=0}^{n}v_{i}}$

${\displaystyle [[x_{1},\ldots ,x_{n}],y_{2},\ldots ,y_{n}]]=\sum _{i=1}^{n}[x_{1},\ldots ,x_{i-1},[x_{i},y_{2},\ldots ,y_{n}],x_{i+1},\ldots ,x_{n}],}$

y así dota a R ⁿ⁺¹ de una estructura de álgebra de n-Lie (ver Proposición 1 de ^[24] ).

Historia

En 1773, Joseph-Louis Lagrange utilizó la forma componente de los productos punto y cruz para estudiar el tetraedro en tres dimensiones. ^{[25] [nota 3]}

En 1843, William Rowan Hamilton introdujo el producto cuaternión , y con él los términos vector y escalar . Dados dos cuaterniones [0, u ] y [0, v ] , donde u y v son vectores en R ³ , su producto de cuaternión se puede resumir como [− u ⋅ v , u × v ] . James Clerk Maxwell utilizó las herramientas de los cuaterniones de Hamilton para desarrollar sus famosas ecuaciones de electromagnetismo , y por esta y otras razones los cuaterniones durante un tiempo fueron una parte esencial de la educación física.

En 1844, Hermann Grassmann publicó un álgebra geométrica no ligada a la dimensión dos o tres. Grassmann desarrolló varios productos, incluido un producto cruzado representado entonces por [uv] . ^[26] ( Ver también: álgebra exterior . )

En 1853, Augustin-Louis Cauchy , contemporáneo de Grassmann, publicó un artículo sobre claves algebraicas que se utilizaban para resolver ecuaciones y tenían las mismas propiedades de multiplicación que el producto cruz. ^{[27] [28]}

En 1878, William Kingdon Clifford publicó Elements of Dynamic , en el que se atestigua el término producto vectorial . En el libro, se define que este producto de dos vectores tiene magnitud igual al área del paralelogramo del que son dos lados y dirección perpendicular a su plano. ^[29] ( Ver también: Álgebra de Clifford . )

En apuntes de conferencias de 1881, Gibbs representó el producto cruzado por y lo llamó producto sesgado . ^{[30] [31]} En 1901, el alumno de Gibb, Edwin Bidwell Wilson, editó y amplió estas notas de clase en el libro de texto Análisis vectorial . Wilson mantuvo el término producto sesgado , pero observó que los términos alternativos producto cruzado ^{[nota 4]} y producto vectorial eran más frecuentes. ^[32] ${\displaystyle u\times v}$

En 1908, Cesare Burali-Forti y Roberto Marcolongo introdujeron la notación de producto vectorial u ∧ v . ^[26] Esto se usa en Francia y otras áreas hasta el día de hoy, ya que el símbolo ya se usa para denotar la multiplicación y el producto cartesiano . ${\displaystyle \times }$

Ver también

• Producto cartesiano : producto de dos conjuntos.
• Álgebra geométrica: sistemas giratorios
• Productos cruzados múltiples : productos que involucran más de tres vectores
• Multiplicación de vectores
• Producto cuádruple
• × (el símbolo)

Notas

1. Aquí, "formal" significa que esta notación tiene la forma de un determinante, pero no se adhiere estrictamente a la definición; es un mnemónico utilizado para recordar la expansión del producto cruzado.
2. Por forma de volumen se entiende una función que toma n vectores y da un escalar, el volumen del paralelotopo definido por los vectores: esta es una forma sesgada-simétrica multilineal n -aria. En presencia de una base, como esta viene dada por el determinante, pero en un espacio vectorial abstracto, esta es una estructura agregada. En términos de estructuras G , una forma de volumen es una estructura. ${\displaystyle V\times \cdots \times V\to \mathbf {R} .}$ ${\displaystyle \mathbf {R} ^{n},}$ ${\displaystyle SL}$
3. En notación moderna, Lagrange define , y . Por tanto, lo moderno corresponde a las tres variables en la notación de Lagrange. ${\displaystyle \mathbf {\xi } =\mathbf {y} \times \mathbf {z} }$ ${\displaystyle {\boldsymbol {\eta }}=\mathbf {z} \times \mathbf {x} }$ ${\displaystyle {\boldsymbol {\zeta }}=\mathbf {x} \times {\boldsymbol {y}}}$ ${\displaystyle \mathbf {x} }$ ${\displaystyle (x,x',x'')}$
4. ya que A × B se lee como " A cruz B "

Referencias

1. Weisstein, Eric W. "Producto cruzado". Wolfram MathWorld . Consultado el 6 de septiembre de 2020 .
2. "Producto cruzado". www.mathsisfun.com . Consultado el 6 de septiembre de 2020 .
3. Massey, William S. (diciembre de 1983). "Productos cruzados de vectores en espacios euclidianos de dimensiones superiores" (PDF) . El Mensual Matemático Estadounidense . 90 (10): 697–701. doi :10.2307/2323537. JSTOR  2323537. S2CID  43318100. Archivado desde el original (PDF) el 26 de febrero de 2021. Si se requieren sólo tres propiedades básicas del producto vectorial... resulta que un producto vectorial de vectores existe sólo en el espacio euclidiano de 3 y 7 dimensiones.
4. Arfken, George B. Métodos matemáticos para físicos (4ª ed.). Elsevier.
5. Jeffreys, H.; Jeffreys, BS (1999). Métodos de física matemática . Prensa de la Universidad de Cambridge. OCLC  41158050.
6. Acheson, DJ (1990). Dinámica de fluidos elemental . Prensa de la Universidad de Oxford. ISBN 0198596790.
7. Howison, Sam (2005). Matemáticas Prácticas Aplicadas . Prensa de la Universidad de Cambridge. ISBN 0521842743.
8. Wilson 1901, pag. 60–61.
9. Dennis G. Zill; Michael R. Cullen (2006). "Definición 7.4: Producto cruzado de dos vectores". Matemáticas de ingeniería avanzada (3ª ed.). Aprendizaje de Jones y Bartlett. pag. 324.ISBN​ 0-7637-4591-X.
10. Edwin Bidwell Wilson (1913). "Capítulo II. Productos directos y sesgados de vectores". Análisis vectorial . Fundado en las conferencias de J. William Gibbs. New Haven: Prensa de la Universidad de Yale.El producto escalar se denomina "producto directo" y el producto cruzado se denomina "producto sesgado".
11. Una historia del análisis vectorial por Michael J. Crowe, Math. Universidad de California Davis.
12. Dennis G. Zill; Michael R. Cullen (2006). "Ecuación 7: a × b como suma de determinantes".trabajo citado. Aprendizaje de Jones y Bartlett. pag. 321.ISBN​ 0-7637-4591-X.
13. Señor Spiegel; S. Lipschutz; D. Spellman (2009). Análisis vectorial . Los esquemas de Schaum. McGraw-Hill. pag. 29.ISBN​ 978-0-07-161545-7.
14. WS Massey (diciembre de 1983). "Productos cruzados de vectores en espacios euclidianos de dimensiones superiores". El Mensual Matemático Estadounidense . El American Mathematical Monthly, vol. 90, núm. 10. 90 (10): 697–701. doi :10.2307/2323537. JSTOR  2323537.
15. Vladimir A. Boichenko; Gennadiĭ Alekseevich Leonov; Volker Reitmann (2005). Teoría de dimensiones para ecuaciones diferenciales ordinarias. Vieweg+Teubner Verlag. pag. 26.ISBN​ 3-519-00437-2.
16. Pertti Lounesto (2001). Álgebras y espinores de Clifford (2ª ed.). Prensa de la Universidad de Cambridge. pag. 94.ISBN​ 0-521-00551-5.
17. Shuangzhe Liu; Gõtz Trenkler (2008). "Hadamard, Khatri-Rao, Kronecker y otros productos matriciales". Int J Ciencias de la Información y Sistemas . Instituto de informática y educación científica. 4 (1): 160-177.
18. por Eric W. Weisstein (2003). "Identidad Binet-Cauchy". Enciclopedia concisa de matemáticas CRC (2ª ed.). Prensa CRC. pag. 228.ISBN​ 1-58488-347-2.
19. Lounesto, Pertti (2001). Álgebras de Clifford y espinores . Cambridge: Prensa de la Universidad de Cambridge. págs.193 . ISBN 978-0-521-00551-7.
20. Greub, W. (1978). Álgebra multilineal .
21. Hogben, L , ed. (2007). Manual de álgebra lineal .^{[ página necesaria ]}
22. Arturo, John W. (2011). Comprensión del álgebra geométrica para la teoría electromagnética. Prensa IEEE . pag. 49.ISBN​ 978-0470941638.
23. Doran, Chris; Lasenby, Anthony (2003). Álgebra geométrica para físicos. Prensa de la Universidad de Cambridge . págs. 401–408. ISBN 978-0521715959.
24. Filippov, VT (1985). "Álgebras de n-Lie". Sibirsk. Estera. Z h . 26 (6): 879–891. doi :10.1007/BF00969110. S2CID  125051596.
25. Lagrange, Joseph-Louis (1773). "Soluciones analíticas de quelques problèmes sur les pirámides triangulares". Obras. vol. 3. pág. 661.
26. Cajori (1929), pág. 134.
27. Crowe (1994), pág. 83.
28. Cauchy, Augustin-Louis (1900). Obras . vol. 12. pág. dieciséis.
29. William Kingdon Clifford (1878) Elementos de dinámica, parte I, página 95, Londres: MacMillan & Co
30. Gibbs, Josías Willard (1884). Elementos de análisis vectorial: dispuestos para el uso de estudiantes de física. New Haven: Impreso por Tuttle, Morehouse & Taylor.
31. Crowe (1994), pág. 154.
32. Wilson (1901), pág. 61.

Bibliografía

• Cajori, Florián (1929). Una historia de las notaciones matemáticas Volumen II. Publicaciones de corte abierta . pag. 134.ISBN​ 978-0-486-67766-8.
• Crowe, Michael J. (1994). Una historia del análisis vectorial . Dover. ISBN 0-486-67910-1.
• EA Milne (1948) Mecánica vectorial , Capítulo 2: Producto vectorial, págs. 11 a 31, Londres: Methuen Publishing .
• Wilson, Edwin Bidwell (1901). Análisis vectorial: un libro de texto para uso de estudiantes de matemáticas y física, basado en las conferencias de J. Willard Gibbs. Prensa de la Universidad de Yale .
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (en italiano). Bolonia: Zanichelli editore.

enlaces externos

• "Producto cruzado", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Una rápida derivación geométrica e interpretación de productos cruzados.
• Un tutorial interactivo creado en la Universidad de Syracuse – (requiere java )
• W. Kahan (2007). Productos cruzados y rotaciones en el espacio euclidiano 2 y 3. Universidad de California, Berkeley (PDF).
• El producto vectorial, Mathcentre (Reino Unido), 2009