Cuaternio

Extensión no conmutativa de los números complejos.

Gráfico de Cayley Q8 que muestra los seis ciclos de multiplicación por i , j y k . (Si la imagen se abre en Wikimedia Commons haciendo clic dos veces en ella, los ciclos se pueden resaltar al pasar el cursor sobre ellos o hacer clic sobre ellos).

En matemáticas , el sistema numérico de cuaterniones extiende los números complejos . Los cuaterniones fueron descritos por primera vez por el matemático irlandés William Rowan Hamilton en 1843 ^{[1] [2]} y aplicados a la mecánica en el espacio tridimensional . El álgebra de cuaterniones a menudo se denota por H (por Hamilton ), o en negrita por. Aunque la multiplicación de cuaterniones no es conmutativa , da una definición del cociente de dos vectores en un espacio tridimensional. ^{[3] [4]} Los cuaterniones generalmente se representan en la forma ${\displaystyle \mathbb {H} .}$

$${\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} ,}$$

donde los coeficientes a , b , c , d son números reales , y 1, i , j , k son los vectores base o elementos base . ^[5]

Los cuaterniones se utilizan en matemáticas puras , pero también tienen usos prácticos en matemáticas aplicadas , particularmente para cálculos que involucran rotaciones tridimensionales , como en gráficos por computadora tridimensionales , visión por computadora , imágenes por resonancia magnética ^[6] y análisis de texturas cristalográficas . ^[7] Se pueden utilizar junto con otros métodos de rotación, como los ángulos de Euler y las matrices de rotación , o como alternativa a ellos, según la aplicación.

En términos modernos, los cuaterniones forman un álgebra de división normada asociativa de cuatro dimensiones sobre los números reales y, por lo tanto, un anillo, también un anillo de división y un dominio . Es un caso especial de álgebra de Clifford , clasificada como Fue la primera álgebra de división no conmutativa descubierta. ${\displaystyle \operatorname {Cl} _{0,2}(\mathbb {R} )\cong \operatorname {Cl} _{3,0}^{+}(\mathbb {R} ).}$

Según el teorema de Frobenius , el álgebra es uno de los dos únicos anillos de división de dimensión finita que contienen un subanillo propio isomorfo a los números reales; el otro son los números complejos. Estos anillos también son álgebras euclidianas de Hurwitz , de las cuales los cuaterniones son el álgebra asociativa más grande (y por tanto el anillo más grande). Extendiendo aún más los cuaterniones se obtienen los octoniones no asociativos , que es el último álgebra de división normada de los números reales. La siguiente extensión da los sedeniones , que tienen divisores cero y por lo tanto no pueden ser un álgebra de división normada. ^[8] ${\displaystyle \mathbb {H} }$

Los cuaterniones unitarios dan una estructura de grupo en las 3 esferas S ³ isomorfa a los grupos Spin(3) y SU(2) , es decir, el grupo de cobertura universal de SO(3) . Los vectores de base positivos y negativos forman el grupo de cuaterniones de ocho elementos .

Representación gráfica de productos de unidades de cuaterniones como rotaciones de 90° en los planos del espacio de 4 dimensiones abarcado por dos de {1, i , j , k }. Se puede considerar que el factor izquierdo gira con el factor derecho para llegar al producto. Visualmente i  ⋅  j = − ( j  ⋅  i ) .

• En azul :
  • 1  ⋅ i = i    (1/ i plano)
  • yo  ⋅ j = k    ( i / k plano)
• En rojo :
  • 1  ⋅ j = j    (1/ j plano)
  • j  ⋅ i = − k    ( j / k plano)

Historia

Placa del cuaternión en el puente Brougham (Broom) , Dublín , que dice:

     Aquí, mientras pasaba
el 16 de octubre de 1843,
Sir William Rowan Hamilton,
en un destello de genio, descubrió
la fórmula fundamental para
la multiplicación de cuaterniones
     i ² = j ² = k ² = i  j  k = −1
y la cortó en una piedra de este puente

Los cuaterniones fueron introducidos por Hamilton en 1843. ^[9] Los precursores importantes de este trabajo incluyeron la identidad de los cuatro cuadrados de Euler (1748) y la parametrización de las rotaciones generales mediante cuatro parámetros de Olinde Rodrigues (1840), pero ninguno de estos escritores trató los cuatro parámetros. rotaciones como álgebra. ^{[10] [11]} Carl Friedrich Gauss también había descubierto los cuaterniones en 1819, pero este trabajo no se publicó hasta 1900. ^{[12] [13]}

Hamilton sabía que los números complejos podían interpretarse como puntos en un plano y estaba buscando una manera de hacer lo mismo con puntos en el espacio tridimensional . Los puntos en el espacio se pueden representar por sus coordenadas, que son ternas de números, y desde hacía muchos años sabía sumar y restar ternas de números. Sin embargo, durante mucho tiempo estuvo estancado en el problema de la multiplicación y la división. No sabía cómo calcular el cociente de las coordenadas de dos puntos en el espacio. De hecho, Ferdinand Georg Frobenius demostró más tarde en 1877 que para que un álgebra de división de números reales sea de dimensión finita y asociativa, no puede ser tridimensional, y sólo existen tres álgebras de división de este tipo: (números complejos) y (cuaterniones ). ) que tienen dimensiones 1, 2 y 4 respectivamente. ${\displaystyle \mathbb {R,C} }$ ${\displaystyle \mathbb {H} }$

El gran avance en materia de cuaterniones se produjo finalmente el lunes 16 de octubre de 1843 en Dublín , cuando Hamilton se dirigía a la Real Academia Irlandesa para presidir una reunión del consejo. Mientras caminaba por el camino de sirga del Canal Real con su esposa, los conceptos detrás de los cuaterniones iban tomando forma en su mente. Cuando se le ocurrió la respuesta, Hamilton no pudo resistir la tentación de esculpir la fórmula de los cuaterniones.

$${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1}$$

en la piedra del puente Brougham mientras se detenía en él. Aunque la talla se ha desvanecido desde 1989, ha habido una peregrinación anual llamada Hamilton Walk para científicos y matemáticos que caminan desde el Observatorio Dunsink hasta el puente del Canal Real en recuerdo del descubrimiento de Hamilton.

Al día siguiente, Hamilton escribió una carta a su amigo y colega matemático, John T. Graves , describiendo la línea de pensamiento que condujo a su descubrimiento. Esta carta se publicó más tarde en una carta dirigida a la Revista Filosófica y al Journal of Science de Londres, Edimburgo y Dublín ; ^[14] Hamilton afirma:

Y aquí se me ocurrió la idea de que debemos admitir, en algún sentido, una cuarta dimensión del espacio para calcular con ternas... Un circuito eléctrico pareció cerrarse y una chispa surgió. ^[14]

Hamilton llamó cuaternión a un cuádruple con estas reglas de multiplicación , y dedicó la mayor parte del resto de su vida a estudiarlas y enseñarlas. El tratamiento de Hamilton es más geométrico que el enfoque moderno, que enfatiza las propiedades algebraicas de los cuaterniones . Fundó una escuela de "cuaternionistas" y trató de popularizar los cuaterniones en varios libros. El último y más largo de sus libros, Elements of Quaternions , ^[15] tenía 800 páginas; fue editado por su hijo y publicado poco después de su muerte.

Tras la muerte de Hamilton, el físico matemático escocés Peter Tait se convirtió en el principal exponente de los cuaterniones. En ese momento, los cuaterniones eran un tema de examen obligatorio en Dublín. Los temas de física y geometría que ahora se describirían utilizando vectores, como la cinemática en el espacio y las ecuaciones de Maxwell , se describieron enteramente en términos de cuaterniones. Incluso existía una asociación de investigación profesional, la Quaternion Society , dedicada al estudio de los cuaterniones y otros sistemas numéricos hipercomplejos .

Desde mediados de la década de 1880, los cuaterniones comenzaron a ser desplazados por el análisis vectorial , que había sido desarrollado por Josiah Willard Gibbs , Oliver Heaviside y Hermann von Helmholtz . El análisis vectorial describió los mismos fenómenos que los cuaterniones, por lo que tomó prestadas algunas ideas y terminología de la literatura sobre cuaterniones. Sin embargo, el análisis vectorial era conceptualmente más simple y notacionalmente más limpio y, finalmente, los cuaterniones quedaron relegados a un papel menor en matemáticas y física . Un efecto secundario de esta transición es que la obra de Hamilton resulta difícil de comprender para muchos lectores modernos. Las definiciones originales de Hamilton son desconocidas y su estilo de escritura era prolijo y difícil de seguir.

Sin embargo, los cuaterniones han resurgido desde finales del siglo XX, principalmente debido a su utilidad para describir rotaciones espaciales . Las representaciones de rotaciones por cuaterniones son más compactas y más rápidas de calcular que las representaciones por matrices . Además, a diferencia de los ángulos de Euler, no son susceptibles al " bloqueo del cardán ". Por esta razón, los cuaterniones se utilizan en gráficos por computadora , ^{[16] [17]} visión por computadora , robótica , ^[18] muestreo de imágenes de resonancia magnética nuclear , ^[6] teoría de control , procesamiento de señales , control de actitud , física , bioinformática , dinámica molecular , simulaciones por computadora y mecánica orbital . Por ejemplo, es común que los sistemas de control de actitud de las naves espaciales estén comandados en términos de cuaterniones. Los cuaterniones han recibido otro impulso de la teoría de números debido a sus relaciones con las formas cuadráticas . ^[19]

Cuaterniones en física

El descubrimiento de 1924 de que en mecánica cuántica el espín de un electrón y otras partículas de materia (conocidas como espinores ) puede describirse utilizando cuaterniones (en forma de las famosas matrices de espín de Pauli) impulsó su interés; Los cuaterniones ayudaron a comprender cómo se pueden distinguir las rotaciones de los electrones de 360° de las de 720° (el " truco de las placas "). ^{[20] [21]} A partir de 2018 ^[update], su uso no ha superado a los grupos de rotación . ^[a]

Definición

Un cuaternión es una expresión de la forma

$${\displaystyle a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} \ ,}$$

donde a , b , c , d son números reales, e i , j , k son símbolos que pueden interpretarse como vectores unitarios que apuntan a lo largo de los tres ejes espaciales. En la práctica, si uno de a , b , c , d es 0, se omite el término correspondiente; si a , b , c , d son todos cero, el cuaternión es el cuaternión cero , denotado 0; si uno de b , c , d es igual a 1, el término correspondiente se escribe simplemente i , j o ​​k .

Hamilton describe un cuaternión como si consta de una parte escalar y una parte vectorial. El cuaternión se llama parte vectorial (a veces parte imaginaria ) de q , y a es la parte escalar (a veces parte real ) de q . Un cuaternión que es igual a su parte real (es decir, su parte vectorial es cero) se llama cuaternión escalar o real , y se identifica con el número real correspondiente. Es decir, los números reales están incrustados en los cuaterniones. (Más propiamente, el campo de los números reales es isomorfo a un subconjunto de los cuaterniones. El campo de los números complejos también es isomorfo a tres subconjuntos de cuaterniones). ^[22] Un cuaternión que es igual a su parte vectorial se llama cuaternión vectorial . ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ ${\displaystyle b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$

El conjunto de cuaterniones es un espacio vectorial de 4 dimensiones sobre los números reales, teniendo como base la suma de componentes ${\displaystyle \left\{1,\mathbf {i} ,\mathbf {j} ,\mathbf {k} \right\}}$

$${\displaystyle {\begin{aligned}&(a_{1}+b_{1}\,\mathbf {i} +c_{1}\,\mathbf {j} +d_{1}\,\mathbf {k} )+(a_{2}+b_{2}\,\mathbf {i} +c_{2}\,\mathbf {j} +d_{2}\,\mathbf {k} )\\[3mu]&\qquad =(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathbf {i} +(c_{1}+c_{2})\,\mathbf {j} +(d_{1}+d_{2})\,\mathbf {k} ,\end{aligned}}}$$

y la multiplicación escalar por componentes

$${\displaystyle \lambda (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )=\lambda a+(\lambda b)\,\mathbf {i} +(\lambda c)\,\mathbf {j} +(\lambda d)\,\mathbf {k} .}$$

Una estructura de grupo multiplicativo, llamada producto de Hamilton , denotada por yuxtaposición, se puede definir sobre los cuaterniones de la siguiente manera:

• El cuaternión real 1 es el elemento identidad .
• Los cuaterniones reales conmutan con todos los demás cuaterniones, es decir aq = qa para cada cuaternión q y cada cuaternión real a . En terminología algebraica, esto quiere decir que el campo de los cuaterniones reales es el centro de este álgebra de cuaterniones.
• El producto se da primero para los elementos básicos (ver la siguiente subsección) y luego se extiende a todos los cuaterniones utilizando la propiedad distributiva y la propiedad central de los cuaterniones reales. El producto de Hamilton no es conmutativo , sino asociativo , por lo que los cuaterniones forman un álgebra asociativa sobre los números reales.
• Además, todo cuaternión distinto de cero tiene un inverso con respecto al producto de Hamilton:
  $${\displaystyle (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )^{-1}={\frac {1}{a^{2}+b^{2}+c^{2}+d^{2}}}\,(a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} ).}$$

Así, los cuaterniones forman un álgebra de división.

Multiplicación de elementos básicos.

La multiplicación con 1 de los elementos base i , j y k se define por el hecho de que 1 es una identidad multiplicativa , es decir,

$${\displaystyle \mathbf {i} \,1=1\,\mathbf {i} =\mathbf {i} ,\qquad \mathbf {j} \,1=1\,\mathbf {j} =\mathbf {j} ,\qquad \mathbf {k} \,1=1\,\mathbf {k} =\mathbf {k} \,.}$$

Los productos de otros elementos básicos son

$${\displaystyle {\begin{aligned}\mathbf {i} ^{2}&=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1,\\[5mu]\mathbf {i\,j} &=-\mathbf {j\,i} =\mathbf {k} ,\qquad \mathbf {j\,k} =-\mathbf {k\,j} =\mathbf {i} ,\qquad \mathbf {k\,i} =-\mathbf {i\,k} =\mathbf {j} .\end{aligned}}}$$

Combinando estas reglas,

$${\displaystyle {\begin{aligned}\mathbf {i\,j\,k} &=-1.\end{aligned}}}$$

Centro

El centro de un anillo no conmutativo es el subanillo de elementos c tal que cx = xc para cada x . El centro del álgebra de cuaterniones es el subcampo de los cuaterniones reales. De hecho, forma parte de la definición que los cuaterniones reales pertenecen al centro. Por el contrario, si q = a + b i + c j + d k pertenece al centro, entonces

$${\displaystyle 0=\mathbf {i} \,q-q\,\mathbf {i} =2c\,\mathbf {ij} +2d\,\mathbf {ik} =2c\,\mathbf {k} -2d\,\mathbf {j} \,,}$$

y c = d = 0 . Un cálculo similar con j en lugar de i muestra que también se tiene b = 0 . Por tanto q = a es un cuaternión real .

Los cuaterniones forman un álgebra de división. Esto significa que la no conmutatividad de la multiplicación es la única propiedad que diferencia a los cuaterniones de un campo. Esta no conmutatividad tiene algunas consecuencias inesperadas, entre ellas que una ecuación polinómica sobre los cuaterniones puede tener más soluciones distintas que el grado del polinomio. Por ejemplo, la ecuación z ² + 1 = 0 , tiene infinitas soluciones de cuaterniones, que son los cuaterniones z = b i + c j + d k tales que b ² + c ² + d ² = 1 . Así, estas "raíces de –1" forman una esfera unitaria en el espacio tridimensional de los cuaterniones vectoriales.

producto hamilton

Para dos elementos a ₁ + b ₁ i + c ₁ j + d ₁ k y a ₂ + b ₂ i + c ₂ j + d ₂ k , su producto, llamado producto de Hamilton ( a ₁ + b ₁ i + c ₁ j + d ₁ k ) ( a ₂ + b ₂ i + c ₂ j + d ₂ k ), está determinada por los productos de los elementos base y la ley distributiva . La ley distributiva permite expandir el producto para que sea una suma de productos de elementos básicos. Esto da la siguiente expresión:

$${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&+a_{1}b_{2}\mathbf {i} &&+a_{1}c_{2}\mathbf {j} &&+a_{1}d_{2}\mathbf {k} \\{}+{}&b_{1}a_{2}\mathbf {i} &&+b_{1}b_{2}\mathbf {i} ^{2}&&+b_{1}c_{2}\mathbf {ij} &&+b_{1}d_{2}\mathbf {ik} \\{}+{}&c_{1}a_{2}\mathbf {j} &&+c_{1}b_{2}\mathbf {ji} &&+c_{1}c_{2}\mathbf {j} ^{2}&&+c_{1}d_{2}\mathbf {jk} \\{}+{}&d_{1}a_{2}\mathbf {k} &&+d_{1}b_{2}\mathbf {ki} &&+d_{1}c_{2}\mathbf {kj} &&+d_{1}d_{2}\mathbf {k} ^{2}\end{alignedat}}}$$

Ahora los elementos base se pueden multiplicar usando las reglas dadas anteriormente para obtener: ^[9]

$${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&-b_{1}b_{2}&&-c_{1}c_{2}&&-d_{1}d_{2}\\{}+{}(&a_{1}b_{2}&&+b_{1}a_{2}&&+c_{1}d_{2}&&-d_{1}c_{2})\mathbf {i} \\{}+{}(&a_{1}c_{2}&&-b_{1}d_{2}&&+c_{1}a_{2}&&+d_{1}b_{2})\mathbf {j} \\{}+{}(&a_{1}d_{2}&&+b_{1}c_{2}&&-c_{1}b_{2}&&+d_{1}a_{2})\mathbf {k} \end{alignedat}}}$$

El producto de dos cuaterniones de rotación ^[23] será equivalente a la rotación a ₂ + b ₂ i + c ₂ j + d ₂ k seguida de la rotación a ₁ + b ₁ i + c ₁ j + d ₁ k .

Partes escalares y vectoriales

Un cuaternión de la forma a + 0 i + 0 j + 0 k , donde a es un número real, se llama escalar , y un cuaternión de la forma 0 + b i + c j + d k , donde b , c y d son números reales, y al menos uno de b , c o d es distinto de cero, se llama cuaternión vectorial . Si a + b i + c j + d k es cualquier cuaternión, entonces a se llama su parte escalar y b i + c j + d k se llama su parte vectorial . Aunque cada cuaternión puede verse como un vector en un espacio vectorial de cuatro dimensiones, es común referirse a la parte del vector como vectores en un espacio tridimensional. Con esta convención, un vector es lo mismo que un elemento del espacio vectorial ^[b] ${\displaystyle \mathbb {R} ^{3}.}$

Hamilton también llamó cuaterniones vectoriales cuaterniones derechos ^{[25] [26]} y a los números reales (considerados como cuaterniones con parte vectorial cero) cuaterniones escalares .

Si un cuaternión se divide en una parte escalar y una parte vectorial, es decir,

$${\displaystyle \mathbf {q} =(r,\ {\vec {v}}),~~\mathbf {q} \in \mathbb {H} ,~~r\in \mathbb {R} ,~~{\vec {v}}\in \mathbb {R} ^{3},}$$

entonces las fórmulas para la suma, la multiplicación y el inverso multiplicativo son

$${\displaystyle {\begin{aligned}(r_{1},\ {\vec {v}}_{1})+(r_{2},\ {\vec {v}}_{2})&=(r_{1}+r_{2},\ {\vec {v}}_{1}+{\vec {v}}_{2})\,,\\[5mu](r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})&=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2})\,,\\[5mu](r,{\vec {v}})^{-1}&=\left({\frac {r}{r^{2}+{\vec {v}}\cdot {\vec {v}}}},{\frac {-{\vec {v}}}{r^{2}+{\vec {v}}\cdot {\vec {v}}}}\right)\,,\end{aligned}}}$$

donde " " y " " denotan respectivamente el producto escalar y el producto vectorial . ${\displaystyle \cdot }$ ${\displaystyle \times }$

Conjugación, norma y recíproco.

La conjugación de cuaterniones es análoga a la conjugación de números complejos y a la transposición (también conocida como inversión) de elementos de las álgebras de Clifford. Para definirlo, sea un cuaternión. El conjugado de q es el cuaternión . Se denota por q ^∗ , q ^t , o q . ^[9] La conjugación es una involución , lo que significa que es su propia inversa , por lo que conjugar un elemento dos veces devuelve el elemento original. El conjugado de un producto de dos cuaterniones es el producto de los conjugados en orden inverso . Es decir, si p y q son cuaterniones, entonces ( pq ) ^∗ = q ^∗ p ^∗ , no p ^∗ q ^∗ . ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ ${\displaystyle q^{*}=a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} }$ ${\displaystyle {\tilde {q}}}$

La conjugación de un cuaternión, en marcado contraste con la configuración compleja, se puede expresar mediante la multiplicación y suma de cuaterniones:

$${\displaystyle q^{*}=-{\frac {1}{2}}(q+\,\mathbf {i} \,q\,\mathbf {i} +\,\mathbf {j} \,q\,\mathbf {j} +\,\mathbf {k} \,q\,\mathbf {k} ).}$$

La conjugación se puede utilizar para extraer las partes escalar y vectorial de un cuaternión. La parte escalar de p es1/2( p + p ^∗ ) , y la parte vectorial de p es1/2( pags - pags ^∗ ) .

La raíz cuadrada del producto de un cuaternión con su conjugado se llama norma y se denota ‖ q ‖ (Hamilton llamó a esta cantidad tensor de q , pero esto entra en conflicto con el significado moderno de " tensor "). En fórmulas, esto se expresa de la siguiente manera:

$${\displaystyle \lVert q\rVert ={\sqrt {\,qq^{*}~}}={\sqrt {\,q^{*}q~}}={\sqrt {\,a^{2}+b^{2}+c^{2}+d^{2}~}}}$$

Este es siempre un número real no negativo y es igual a la norma euclidiana considerada como espacio vectorial . Multiplicar un cuaternión por un número real aumenta su norma por el valor absoluto del número. Es decir, si α es real, entonces ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{4}}$

$${\displaystyle \lVert \alpha q\rVert =\left|\alpha \right|\,\lVert q\rVert ~.}$$

Este es un caso especial del hecho de que la norma es multiplicativa , lo que significa que

$${\displaystyle \lVert pq\rVert =\lVert p\rVert \,\lVert q\rVert }$$

para dos cuaterniones cualesquiera p y q . La multiplicatividad es una consecuencia de la fórmula del conjugado de un producto. Alternativamente se sigue de la identidad

$${\displaystyle \det {\begin{pmatrix}a+ib&id+c\\id-c&a-ib\end{pmatrix}}=a^{2}+b^{2}+c^{2}+d^{2},}$$

(donde i denota la unidad imaginaria habitual ) y, por tanto, de la propiedad multiplicativa de los determinantes de matrices cuadradas.

Esta norma permite definir la distancia d ( p , q ) entre p y q como norma de su diferencia:

$${\displaystyle d(p,q)=\lVert p-q\rVert ~.}$$

Esto forma un espacio métrico . La suma y la multiplicación son continuas con respecto a la topología métrica asociada . Esto se deduce exactamente con la misma demostración que para los números reales del hecho de que es un álgebra normada. ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {H} }$

unidad cuaternión

Un cuaternión unitario es un cuaternión de norma uno. Dividir un cuaternión q distinto de cero por su norma produce un cuaternión unitario U q llamado versor de q :

$${\displaystyle \mathbf {U} q={\frac {q}{\lVert q\rVert }}.}$$

Cada cuaternión distinto de cero tiene una descomposición polar única , mientras que el cuaternión cero puede formarse a partir de cualquier cuaternión unitario. ${\displaystyle q=\lVert q\rVert \cdot \mathbf {U} q}$

El uso de la conjugación y la norma permite definir el recíproco de un cuaternión distinto de cero. El producto de un cuaternión con su recíproco debe ser igual a 1, y las consideraciones anteriores implican que el producto de y es 1 (para cualquier orden de multiplicación). Entonces el recíproco de q se define como ${\displaystyle q}$ ${\displaystyle q^{*}/\left\Vert q\right\|^{2}}$

$${\displaystyle q^{-1}={\frac {q^{*}}{\lVert q\rVert ^{2}}}.}$$

Dado que la multiplicación no es conmutativa, las cantidades cocientes p q ⁻¹ o q ⁻¹ p   son diferentes (excepto si p y q son múltiplos escalares entre sí o si uno es un escalar): la notaciónpag/qes ambiguo y no debe usarse.

Propiedades algebraicas

Gráfico de Cayley de la pregunta ₈ . Las flechas rojas representan la multiplicación a la derecha por i y las flechas verdes representan la multiplicación a la derecha por j .

El conjunto de todos los cuaterniones es un espacio vectorial sobre los números reales con dimensión  4. ^[c] La multiplicación de cuaterniones es asociativa y se distribuye sobre la suma de vectores, pero con la excepción del subconjunto escalar, no es conmutativa. Por lo tanto, los cuaterniones son un álgebra asociativa no conmutativa sobre los números reales. Aunque contiene copias de los números complejos, no es un álgebra asociativa sobre números complejos. ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$

Como es posible dividir cuaterniones, forman un álgebra de división. Esta es una estructura similar a un campo excepto por la no conmutatividad de la multiplicación. Las álgebras de división asociativa de dimensión finita sobre números reales son muy raras. El teorema de Frobenius establece que hay exactamente tres: , y . La norma convierte los cuaterniones en un álgebra normada , y las álgebras de división normada sobre números reales también son muy raras: el teorema de Hurwitz dice que sólo hay cuatro: , , y (los octoniones). Los cuaterniones son también un ejemplo de álgebra de composición y de álgebra unital de Banach . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {O} }$

Gráfico tridimensional de Q ₈ . Las flechas roja, verde y azul representan la multiplicación por i , j y k , respectivamente. Para mayor claridad, se omite la multiplicación por números negativos.

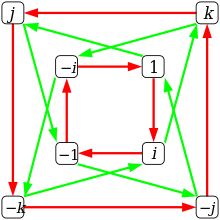
Debido a que el producto de dos vectores de base cualesquiera es más o menos otro vector de base, el conjunto {±1, ± i , ± j , ± k } forma un grupo bajo multiplicación. Este grupo no abeliano se llama grupo cuaternión y se denota Q ₈ . ^[27] El anillo del grupo real de Q ₈ es un anillo que también es un espacio vectorial de ocho dimensiones. Tiene un vector base para cada elemento de Los cuaterniones son isomorfos al anillo cociente de por el ideal generado por los elementos 1 + (−1) , i + (− i ) , j + (− j ) y k + (− k ) . Aquí el primer término en cada una de las diferencias es uno de los elementos básicos 1, i , j y k , y el segundo término es uno de los elementos básicos −1, − i , − j y − k , no los inversos aditivos. de 1, i , j y k . ${\displaystyle \mathbb {R} [\mathrm {Q} _{8}]}$ ${\displaystyle \mathbb {R} .}$ ${\displaystyle \mathrm {Q} _{8}.}$ ${\displaystyle \mathbb {R} [\mathrm {Q} _{8}]}$

Cuaterniones y geometría tridimensional.

La parte vectorial de un cuaternión se puede interpretar como un vector de coordenadas, por lo tanto, las operaciones algebraicas de los cuaterniones reflejan la geometría de Operaciones como el vector punto y los productos cruzados se pueden definir en términos de cuaterniones, y esto hace posible aplicar técnicas de cuaterniones dondequiera que surjan vectores espaciales. Una aplicación útil de los cuaterniones ha sido la de interpolar las orientaciones de fotogramas clave en gráficos por ordenador. ^[dieciséis] ${\displaystyle \mathbb {R} ^{3};}$ ${\displaystyle \mathbb {R} ^{3}.}$

Durante el resto de esta sección, i , j y k denotarán los tres vectores base imaginarios ^[28] de y una base para Reemplazar i por − i , j por − j y k por − k envía un vector a su inverso aditivo , por lo que el inverso aditivo de un vector es el mismo que su conjugado como cuaternión. Por esta razón, a la conjugación a veces se le llama inversa espacial . ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{3}.}$

Para dos cuaterniones vectoriales p = b ₁ i + c ₁ j + d ₁ k y q = b ₂ i + c ₂ j + d ₂ k su producto escalar , por analogía con los vectores en es ${\displaystyle \mathbb {R} ^{3},}$

$${\displaystyle p\cdot q=b_{1}b_{2}+c_{1}c_{2}+d_{1}d_{2}~.}$$

También se puede expresar sin componentes como

$${\displaystyle p\cdot q=\textstyle {\frac {1}{2}}(p^{*}q+q^{*}p)=\textstyle {\frac {1}{2}}(pq^{*}+qp^{*}).}$$

Esto es igual a las partes escalares de los productos pq ^∗ , qp ^∗ , p ^∗ q y q ^∗ p . Tenga en cuenta que sus partes vectoriales son diferentes.

El producto cruzado de p y q con respecto a la orientación determinada por la base ordenada i , j y k es

$${\displaystyle p\times q=(c_{1}d_{2}-d_{1}c_{2})\mathbf {i} +(d_{1}b_{2}-b_{1}d_{2})\mathbf {j} +(b_{1}c_{2}-c_{1}b_{2})\mathbf {k} \,.}$$

(Recuerde que la orientación es necesaria para determinar el signo). Esto es igual a la parte vectorial del producto pq (como cuaterniones), así como a la parte vectorial de − q ^∗ p ^∗ . También tiene la fórmula

$${\displaystyle p\times q=\textstyle {\tfrac {1}{2}}(pq-qp).}$$

Para el conmutador , [ p , q ] = pq − qp , de dos cuaterniones vectoriales se obtiene

$${\displaystyle [p,q]=2p\times q.}$$

En general, sean p y q cuaterniones y escriba

$${\displaystyle {\begin{aligned}p&=p_{\text{s}}+p_{\text{v}},\\[5mu]q&=q_{\text{s}}+q_{\text{v}},\end{aligned}}}$$

donde p _s y q _s son las partes escalares, y p _v y q _v son las partes vectoriales de p y q . Entonces tenemos la fórmula

$${\displaystyle pq=(pq)_{\text{s}}+(pq)_{\text{v}}=(p_{\text{s}}q_{\text{s}}-p_{\text{v}}\cdot q_{\text{v}})+(p_{\text{s}}q_{\text{v}}+q_{\text{s}}p_{\text{v}}+p_{\text{v}}\times q_{\text{v}}).}$$

Esto muestra que la no conmutatividad de la multiplicación de cuaterniones proviene de la multiplicación de cuaterniones vectoriales. También muestra que dos cuaterniones conmutan si y sólo si sus partes vectoriales son colineales. Hamilton ^[29] demostró que este producto calcula el tercer vértice de un triángulo esférico a partir de dos vértices dados y sus longitudes de arco asociadas, que también es un álgebra de puntos en geometría elíptica .

Los cuaterniones unitarios se pueden identificar con rotaciones y Hamilton los llamó versores . ^[29] Consulte también Cuaterniones y rotación espacial para obtener más información sobre el modelado de rotaciones tridimensionales utilizando cuaterniones. ${\displaystyle \mathbb {R} ^{3}}$

Véase Hanson (2005) ^[30] para la visualización de cuaterniones.

Representaciones matriciales

Así como los números complejos se pueden representar como matrices , también se pueden representar los cuaterniones. Hay al menos dos formas de representar cuaterniones como matrices de tal manera que la suma y multiplicación de cuaterniones correspondan a la suma y multiplicación de matrices . Una es utilizar matrices complejas de 2 × 2 y la otra es utilizar matrices reales de 4 × 4. En cada caso, la representación dada pertenece a una familia de representaciones linealmente relacionadas. En la terminología del álgebra abstracta , estos son homomorfismos inyectivos desde los anillos de la matriz M(2, C ) y M(4, R ) , respectivamente. ${\displaystyle \mathbb {H} }$

El cuaternión a + b i + c j + d k se puede representar usando una matriz compleja de 2 × 2 como

${\displaystyle \left[{\begin{array}{rr}a+bi&c+di\\-c+di&a-bi\end{array}}\right].}$

Esta representación tiene las siguientes propiedades:

• Restringir dos cualesquiera de b , cyd a cero produce una representación de números complejos. Por ejemplo, establecer c = d = 0 produce una representación matricial compleja diagonal de números complejos, y establecer b = d = 0 produce una representación matricial real.
• La norma de un cuaternión (la raíz cuadrada del producto con su conjugado, como ocurre con los números complejos) es la raíz cuadrada del determinante de la matriz correspondiente. ^[31]
• El conjugado de un cuaternión corresponde a la transpuesta conjugada de la matriz.
• Por restricción, esta representación produce un isomorfismo entre el subgrupo de cuaterniones unitarios y su imagen SU(2) . Topológicamente, los cuaterniones unitarios son de 3 esferas, por lo que el espacio subyacente de SU(2) también es de 3 esferas. El grupo SU(2) es importante para describir el espín en mecánica cuántica; ver matrices de Pauli .
• Existe una fuerte relación entre las unidades de cuaterniones y las matrices de Pauli. Obtenga las ocho matrices unitarias de cuaterniones tomando a , b , c y d , establezca tres de ellas en cero y la cuarta en 1 o −1. Multiplicar dos matrices de Pauli cualesquiera siempre produce una matriz unitaria de cuaternión, todas excepto −1. Se obtiene −1 vía i ² = j ² = k ² = ijk = −1 ; por ejemplo, la última igualdad es
  $${\displaystyle ijk=\sigma _{1}\sigma _{2}\sigma _{3}\sigma _{1}\sigma _{2}\sigma _{3}=-1.}$$

Usando matrices reales de 4 × 4, ese mismo cuaternión se puede escribir como

$${\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{array}}\right].\end{aligned}}}$$

Sin embargo, la representación de cuaterniones en M(4, R ) no es única. Por ejemplo, el mismo cuaternión también se puede representar como

$${\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&d&-b&-c\\-d&a&c&-b\\b&-c&a&-d\\c&b&d&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right].\end{aligned}}}$$

Existen 48 representaciones matriciales distintas de esta forma en las que una de las matrices representa la parte escalar y las otras tres son todas asimétricas. Más precisamente, hay 48 conjuntos de cuádruples de matrices con estas restricciones de simetría, de modo que una función que envía 1, i , j y k a las matrices del cuádruple es un homomorfismo, es decir, envía sumas y productos de cuaterniones a sumas. y productos de matrices. ^[32] En esta representación, el conjugado de un cuaternión corresponde a la transpuesta de la matriz. La cuarta potencia de la norma de un cuaternión es el determinante de la matriz correspondiente. Al igual que con la representación compleja de 2 × 2 anterior, los números complejos se pueden producir nuevamente restringiendo los coeficientes adecuadamente; por ejemplo, como matrices diagonales de bloques con dos bloques de 2 × 2 estableciendo c = d = 0 .

Cada representación matricial de cuaterniones de 4 × 4 corresponde a una tabla de multiplicar de cuaterniones unitarios. Por ejemplo, la última representación matricial dada arriba corresponde a la tabla de multiplicar.

que es isomorfo - a través de - a ${\displaystyle \{a\mapsto 1,b\mapsto i,c\mapsto j,d\mapsto k\}}$

Al restringir cualquier tabla de multiplicar para que tenga la identidad en la primera fila y columna y que los signos de los encabezados de las filas sean opuestos a los de los encabezados de las columnas, entonces hay 3 opciones posibles para la segunda columna (ignorando el signo), 2 posibles opciones para la tercera columna (signo de ignorar) y 1 opción posible para la cuarta columna (signo de ignorar); eso hace 6 posibilidades. Luego, se puede elegir que la segunda columna sea positiva o negativa, la tercera columna se puede elegir para que sea positiva o negativa y la cuarta columna se puede elegir para que sea positiva o negativa, lo que da 8 posibilidades para el signo. Multiplicar las posibilidades para las posiciones de las letras y sus signos produce 48. Luego, reemplazando 1 con a , i con b , j con c y k con d y eliminando los encabezados de filas y columnas se obtiene una representación matricial de a + b i + c. j + re k .

Teorema de los cuatro cuadrados de Lagrange

Los cuaterniones también se utilizan en una de las pruebas del teorema de los cuatro cuadrados de Lagrange en teoría de números , que establece que todo número entero no negativo es la suma de cuatro cuadrados enteros. Además de ser un teorema elegante por derecho propio, el teorema de los cuatro cuadrados de Lagrange tiene aplicaciones útiles en áreas de las matemáticas fuera de la teoría de números, como la teoría del diseño combinatorio . La prueba basada en cuaterniones utiliza cuaterniones de Hurwitz , un subanillo del anillo de todos los cuaterniones para el que existe un análogo del algoritmo euclidiano .

Cuaterniones como pares de números complejos

Los cuaterniones se pueden representar como pares de números complejos. Desde esta perspectiva, los cuaterniones son el resultado de aplicar la construcción de Cayley-Dickson a los números complejos. Ésta es una generalización de la construcción de los números complejos como pares de números reales.

Sea un espacio vectorial bidimensional sobre números complejos. Elija una base que consta de dos elementos 1 y j . Un vector en se puede escribir en términos de los elementos base 1 y j como ${\displaystyle \mathbb {C} ^{2}}$ ${\displaystyle \mathbb {C} ^{2}}$

$${\displaystyle (a+bi)1+(c+di)\mathbf {j} \,.}$$

Si definimos j ² = −1 y i j = − j i , entonces podemos multiplicar dos vectores usando la ley distributiva. Usar k como notación abreviada para el producto i j conduce a las mismas reglas de multiplicación que los cuaterniones habituales. Por lo tanto, el vector de números complejos anterior corresponde al cuaternión a + bi + c j + d k . Si escribimos los elementos de pares ordenados y cuaterniones como cuádruples, entonces la correspondencia es ${\displaystyle \mathbb {C} ^{2}}$

$${\displaystyle (a+bi,\ c+di)\leftrightarrow (a,b,c,d).}$$

Raíces cuadradas

Raíces cuadradas de −1

En los números complejos, hay exactamente dos números, i y −i , que dan −1 cuando se elevan al cuadrado. Hay infinitas raíces cuadradas de menos uno: la solución del cuaternión para la raíz cuadrada de −1 es la esfera unitaria en Para ver esto, sea q = a + b i + c j + d k un cuaternión, y supongamos que su cuadrado es −1. En términos de a , b , c y d , esto significa ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{3}.}$

$${\displaystyle {\begin{aligned}a^{2}-b^{2}-c^{2}-d^{2}&=-1,{\vphantom {x^{|}}}\\[3mu]2ab&=0,\\[3mu]2ac&=0,\\[3mu]2ad&=0.\end{aligned}}}$$

Para satisfacer las últimas tres ecuaciones, a = 0 o b , c y d son todos 0. Esto último es imposible porque a es un número real y la primera ecuación implicaría que a ² = −1 . Por lo tanto, a = 0 y b ² + c ² + d ² = 1 . En otras palabras: un cuaternión se eleva a −1 si y solo si es un cuaternión vectorial con norma 1. Por definición, el conjunto de todos esos vectores forma la esfera unitaria.

Sólo los cuaterniones reales negativos tienen infinitas raíces cuadradas. Todos los demás tienen sólo dos (o uno en el caso de 0). ^{[ cita necesaria ] [d]}

Como unión de planos complejos.

Cada par antípoda de raíces cuadradas de −1 crea una copia distinta de los números complejos dentro de los cuaterniones. Si q ² = −1 , entonces la copia es la imagen de la función

$${\displaystyle a+bi\mapsto a+bq\,.}$$

Se trata de un homomorfismo de anillo inyectivo desde hasta que define un isomorfismo de campo desde hasta su imagen . Las imágenes de las incrustaciones correspondientes a q y − q son idénticas. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} ,}$ ${\displaystyle \mathbb {C} }$

Cada cuaternión no real genera una subálgebra de los cuaterniones que es isomorfa y, por tanto, es un subespacio plano de escritura q como la suma de su parte escalar y su parte vectorial: ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} \colon }$

$${\displaystyle q=q_{s}+{\vec {q}}_{v}.}$$

Descomponga aún más la parte del vector como el producto de su norma y su versor :

$${\displaystyle q=q_{s}+\lVert {\vec {q}}_{v}\rVert \cdot \mathbf {U} {\vec {q}}_{v}=q_{s}+\|{\vec {q}}_{v}\|\,{\frac {{\vec {q}}_{v}}{\|{\vec {q}}_{v}\|}}.}$$

(Esto no es lo mismo que .) El versor de la parte vectorial de q , , es un versor derecho con –1 como cuadrado. Una verificación sencilla muestra que ${\displaystyle q_{s}+\lVert q\rVert \cdot \mathbf {U} q}$ ${\displaystyle \mathbf {U} {\vec {q}}_{v}}$

$${\displaystyle a+bi\mapsto a+b\mathbf {U} {\vec {q}}_{v}}$$

homomorfismoálgebras normadasq ${\displaystyle \mathbb {C} }$ ${\displaystyle q_{s}+\lVert {\vec {q}}_{v}\rVert i}$

Como es la unión de las imágenes de todos estos homomorfismos, se pueden ver los cuaterniones como un lápiz de planos que se cruzan en la recta real . Cada uno de estos planos complejos contiene exactamente un par de puntos antípodas de la esfera de raíces cuadradas de menos uno. ${\displaystyle \mathbb {H} }$

Subanillos conmutativos

La relación de los cuaterniones entre sí dentro de los subplanos complejos de también se puede identificar y expresar en términos de subanillos conmutativos . Específicamente, dado que dos cuaterniones p y q conmutan (es decir, pq = qp ) solo si se encuentran en el mismo subplano complejo de , el perfil de como unión de planos complejos surge cuando se busca encontrar todos los subanillos conmutativos del anillo del cuaternión . ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$

Raíces cuadradas de cuaterniones arbitrarios.

Cualquier cuaternión (representado aquí en representación escalar-vectorial) tiene al menos una raíz cuadrada que resuelve la ecuación . Al observar las partes escalar y vectorial de esta ecuación por separado se obtienen dos ecuaciones, que cuando se resuelven dan las soluciones ${\displaystyle \mathbf {q} =(r,\,{\vec {v}})}$ ${\displaystyle {\sqrt {\mathbf {q} }}=(x,\,{\vec {y}})}$ ${\displaystyle {\sqrt {\mathbf {q} }}^{2}=(x,\,{\vec {y}})^{2}=\mathbf {q} }$

$${\displaystyle {\sqrt {\mathbf {q} }}={\sqrt {(r,\,{\vec {v}}\,)}}=\pm \left({\sqrt {\frac {\|\mathbf {q} \|+r}{2}}},\ {\frac {\vec {v}}{\|{\vec {v}}\|}}{\sqrt {\frac {\|\mathbf {q} \|-r}{2}}}\right),}$$

donde es la norma de y es la norma de . Para cualquier cuaternión escalar , esta ecuación proporciona las raíces cuadradas correctas si se interpreta como un vector unitario arbitrario. ${\textstyle \|{\vec {v}}\|={\sqrt {{\vec {v}}\cdot {\vec {v}}}}={\sqrt {-{\vec {v}}^{2}}}}$ ${\displaystyle {\vec {v}}}$ ${\textstyle \|\mathbf {q} \|={\sqrt {\mathbf {q} ^{*}\mathbf {q} }}=r^{2}+\|{\vec {v}}\|^{2}}$ ${\displaystyle \mathbf {q} }$ ${\displaystyle \mathbf {q} }$ ${\textstyle {\frac {\vec {v}}{\|{\vec {v}}\|}}}$

Por lo tanto, los cuaterniones no escalares, distintos de cero, o cuaterniones escalares positivos, tienen exactamente dos raíces, mientras que 0 tiene exactamente una raíz (0), y los cuaterniones escalares negativos tienen infinitas raíces, que son los cuaterniones vectoriales ubicados en , es decir, donde la parte escalar es cero y la parte vectorial está ubicada en la 2 esferas con radio . ${\displaystyle \{0\}\times S^{2}({\sqrt {-r}})}$ ${\displaystyle {\sqrt {-r}}}$

Funciones de una variable cuaternión

Los conjuntos de Julia y Mandelbrot se pueden extender a los Cuaterniones, pero deben usar secciones transversales para representarse visualmente en 3 dimensiones. Este conjunto de Julia tiene una sección transversal en el plano xy .

Al igual que las funciones de una variable compleja , las funciones de una variable cuaternión sugieren modelos físicos útiles. Por ejemplo, los campos eléctricos y magnéticos originales descritos por Maxwell eran funciones de una variable cuaternión. Ejemplos de otras funciones incluyen la extensión del conjunto de Mandelbrot y los conjuntos de Julia en un espacio de 4 dimensiones. ^[36]

Funciones exponenciales, logaritmicas y de potencia.

Dado un cuaternión,

$${\displaystyle q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+\mathbf {v} ,}$$

el exponencial se calcula como ^[37]

$${\displaystyle \exp(q)=\sum _{n=0}^{\infty }{\frac {q^{n}}{n!}}=e^{a}\left(\cos \|\mathbf {v} \|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\sin \|\mathbf {v} \|\right),}$$

y el logaritmo es ^[37]

$${\displaystyle \ln(q)=\ln \|q\|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\arccos {\frac {a}{\|q\|}}.}$$

De ello se deduce que la descomposición polar de un cuaternión puede escribirse

$${\displaystyle q=\|q\|e^{{\hat {n}}\varphi }=\|q\|\left(\cos(\varphi )+{\hat {n}}\sin(\varphi )\right),}$$

donde el ángulo ^[e] ${\displaystyle \varphi }$

$${\displaystyle a=\|q\|\cos(\varphi )}$$

y el vector unitario está definido por: ${\displaystyle {\hat {n}}}$

$${\displaystyle \mathbf {v} ={\hat {n}}\|\mathbf {v} \|={\hat {n}}\|q\|\sin(\varphi )\,.}$$

Cualquier cuaternión unitario puede expresarse en forma polar como:

$${\displaystyle q=\exp {({\hat {n}}\varphi )}.}$$

La potencia de un cuaternión elevado a un exponente arbitrario (real) x viene dada por:

$${\displaystyle q^{x}=\|q\|^{x}e^{{\hat {n}}x\varphi }=\|q\|^{x}\left(\cos(x\varphi )+{\hat {n}}\,\sin(x\varphi )\right)~.}$$

Norma geodésica

La distancia geodésica d _g ( p , q ) entre los cuaterniones unitarios p y q se define como: ^[39]

$${\displaystyle d_{\text{g}}(p,q)=\lVert \ln(p^{-1}q)\rVert .}$$

y equivale al valor absoluto de la mitad del ángulo subtendido por p y q a lo largo de un gran arco de la esfera S ³ . Este ángulo también se puede calcular a partir del producto escalar del cuaternión sin el logaritmo como:

$${\displaystyle \arccos(2(p\cdot q)^{2}-1).}$$

Grupos de rotación tridimensionales y cuatridimensionales.

La palabra " conjugación ", además del significado dado anteriormente, también puede significar tomar un elemento a a r a r ⁻¹ donde r es algún cuaternión distinto de cero. Todos los elementos que son conjugados a un elemento dado (en este sentido de la palabra conjugado) tienen la misma parte real y la misma norma de la parte vectorial. (Así, el conjugado en el otro sentido es uno de los conjugados en este sentido.) ^[40]

Así, el grupo multiplicativo de cuaterniones distintos de cero actúa por conjugación sobre la copia de cuaterniones formados por parte real igual a cero. La conjugación de un cuaternión unitario (un cuaternión de valor absoluto 1) con parte real cos( φ ) es una rotación de un ángulo 2 φ , siendo el eje de rotación la dirección de la parte vectorial. Las ventajas de los cuaterniones son: ^[41] ${\displaystyle \mathbb {R} ^{3}}$

• Evitar el bloqueo del cardán , un problema con sistemas como los ángulos de Euler.
• Más rápido y compacto que las matrices.
• Representación no singular (en comparación con los ángulos de Euler, por ejemplo).
• Los pares de cuaterniones unitarios representan una rotación en el espacio 4D (ver Rotaciones en el espacio euclidiano de 4 dimensiones: Álgebra de rotaciones 4D ).

El conjunto de todos los cuaterniones unitarios ( versores ) forma una S ³ de 3 esferas y un grupo (un grupo de Lie ) bajo la multiplicación, cubriendo doblemente el grupo de matrices ortogonales reales de 3 × 3  del determinante  1, ya que dos cuaterniones unitarios corresponden a cada rotación bajo la correspondencia anterior. Ver truco del plato . ${\displaystyle {\text{SO}}(3,\mathbb {R} )}$

La imagen de un subgrupo de versores es un grupo de puntos y, a la inversa, la preimagen de un grupo de puntos es un subgrupo de versores. La preimagen de un grupo de puntos finitos recibe el mismo nombre, con el prefijo binario . Por ejemplo, la preimagen del grupo icosaédrico es el grupo icosaédrico binario .

El grupo de versores es isomorfo a SU(2) , el grupo de matrices unitarias complejas 2×2 del determinante 1.

Sea A el conjunto de cuaterniones de la forma a + b i + c j + d k donde a , b, cyd son todos números enteros o todos semienteros . El conjunto A es un anillo (de hecho, un dominio ) y una red y se llama anillo de cuaterniones de Hurwitz. Hay 24 cuaterniones unitarios en este anillo, y son los vértices de una celda regular de 24 con el símbolo de Schläfli {3,4,3}. Corresponden a la doble cubierta del grupo de simetría rotacional del tetraedro regular . De manera similar, los vértices de una celda regular de 600 con símbolo de Schläfli {3,3,5 } pueden tomarse como la unidad icosianos , correspondientes a la doble cobertura del grupo de simetría rotacional del icosaedro regular . La doble cubierta del grupo de simetría rotacional del octaedro regular corresponde a los cuaterniones que representan los vértices del diesfenoidal de 288 celdas . ^[42]

Álgebras de cuaterniones

Los cuaterniones se pueden generalizar en otras álgebras llamadas álgebras de cuaterniones . Considere F como cualquier campo con características diferentes de 2, y a y b como elementos de F ; se puede definir un álgebra asociativa unitaria de cuatro dimensiones sobre F con base 1, i , j e ij , donde i ² = a , j ² = by ij = − ji ( entonces (ij) ² = − ab ) .

Las álgebras de cuaterniones son isomorfas al álgebra de matrices de 2 × 2 sobre F o forman álgebras de división sobre F , dependiendo de la elección de a y b .

Cuaterniones como parte par de Cl 3,0 (R)

La utilidad de los cuaterniones para cálculos geométricos se puede generalizar a otras dimensiones identificando los cuaterniones como la parte par del álgebra de Clifford. Esta es un álgebra multivectorial asociativa construida a partir de elementos básicos fundamentales σ 1 , σ 2 , σ 3 usando las reglas del producto. ${\displaystyle \operatorname {Cl} _{3,0}^{+}(\mathbb {R} )}$ ${\displaystyle \operatorname {Cl} _{3,0}(\mathbb {R} ).}$

$${\displaystyle \sigma _{1}^{2}=\sigma _{2}^{2}=\sigma _{3}^{2}=1,}$$

$${\displaystyle \sigma _{i}\sigma _{j}=-\sigma _{j}\sigma _{i}\qquad (j\neq i).}$$

Si se toman estos elementos básicos fundamentales para representar vectores en el espacio 3D, entonces resulta que la reflexión de un vector r en un plano perpendicular a un vector unitario w se puede escribir:

$${\displaystyle r^{\prime }=-w\,r\,w.}$$

Dos reflexiones hacen una rotación de un ángulo dos veces el ángulo entre los dos planos de reflexión, por lo que

$${\displaystyle r^{\prime \prime }=\sigma _{2}\sigma _{1}\,r\,\sigma _{1}\sigma _{2}}$$

corresponde a una rotación de 180° en el plano que contiene σ ₁ y σ ₂ . Esto es muy similar a la fórmula del cuaternión correspondiente,

$${\displaystyle r^{\prime \prime }=-\mathbf {k} \,r\,\mathbf {k} .}$$

De hecho, las dos estructuras y son isomorfas . Una identificación natural es ${\displaystyle \operatorname {Cl} _{3,0}^{+}(\mathbb {R} )}$ ${\displaystyle \mathbb {H} }$

$${\displaystyle 1\mapsto 1\,,\quad \mathbf {i} \mapsto \sigma _{2}\sigma _{3}\,,\quad \mathbf {j} \mapsto \sigma _{3}\sigma _{1}\,,\quad \mathbf {k} \mapsto \sigma _{1}\sigma _{2}\,,}$$

y es sencillo confirmar que esto preserva las relaciones de Hamilton.

$${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1~.}$$

En esta imagen, los llamados "cuaterniones vectoriales" (es decir, cuaterniones imaginarios puros) no corresponden a vectores sino a bivectores : cantidades con magnitud y orientaciones asociadas con  planos 2D particulares en lugar de  direcciones 1D . La relación con los números complejos también se vuelve más clara: en 2D, con dos direcciones vectoriales σ ₁ y σ ₂ , solo hay un elemento base bivectorial σ ₁ σ ₂ , por lo que solo uno imaginario. Pero en 3D, con tres direcciones vectoriales, hay tres elementos base bivectoriales σ ₂ σ ₃ , σ ₃ σ ₁ , σ ₁ σ ₂ , entonces tres imaginarios.

Este razonamiento se extiende más allá. En el álgebra de Clifford existen seis elementos básicos bivectoriales, ya que con cuatro direcciones vectoriales básicas diferentes se pueden definir seis pares diferentes y, por tanto, seis planos diferentes linealmente independientes. Las rotaciones en dichos espacios utilizando estas generalizaciones de cuaterniones, llamadas rotores , pueden ser muy útiles para aplicaciones que involucran coordenadas homogéneas . Pero sólo en 3D el número de bivectores base es igual al número de vectores base, y cada bivector puede identificarse como un pseudovector . ${\displaystyle \operatorname {Cl} _{4,0}(\mathbb {R} ),}$

Hay varias ventajas al colocar cuaterniones en este entorno más amplio: ^[43]

• Los rotores son una parte natural del álgebra geométrica y se entienden fácilmente como la codificación de una doble reflexión.
• En álgebra geométrica, un rotor y los objetos sobre los que actúa viven en el mismo espacio. Esto elimina la necesidad de cambiar representaciones y codificar nuevas estructuras y métodos de datos, lo que tradicionalmente se requiere cuando se aumenta el álgebra lineal con cuaterniones.
• Los rotores son universalmente aplicables a cualquier elemento del álgebra, no sólo a vectores y otros cuaterniones, sino también a líneas, planos, círculos, esferas, rayos, etc.
• En el modelo conforme de geometría euclidiana, los rotores permiten la codificación de rotación, traslación y escala en un solo elemento del álgebra, actuando universalmente sobre cualquier elemento. En particular, esto significa que los rotores pueden representar rotaciones alrededor de un eje arbitrario, mientras que los cuaterniones están limitados a un eje que pasa por el origen.
• Las transformaciones codificadas por rotor hacen que la interpolación sea particularmente sencilla.
• Los rotores se trasladan naturalmente a espacios pseudoeuclidianos , por ejemplo, el espacio de Minkowski de la relatividad especial . En tales espacios, los rotores se pueden utilizar para representar eficientemente los impulsos de Lorentz y para interpretar fórmulas que involucran las matrices gamma .

Para obtener más detalles sobre los usos geométricos de las álgebras de Clifford, consulte Álgebra geométrica .

grupo brauer

Los cuaterniones son "esencialmente" la única (no trivial) álgebra simple central (CSA) sobre los números reales, en el sentido de que cada CSA sobre los números reales es equivalente de Brauer a los números reales o a los cuaterniones. Explícitamente, el grupo de Brauer de los números reales consta de dos clases, representadas por los números reales y los cuaterniones, donde el grupo de Brauer es el conjunto de todos los CSA, hasta la relación de equivalencia de que un CSA sea un anillo matricial sobre otro. Según el teorema de Artin-Wedderburn (específicamente, la parte de Wedderburn), los CSA son todos álgebras matriciales sobre un álgebra de división y, por lo tanto, los cuaterniones son el único álgebra de división no trivial sobre los números reales.

Los CSA (anillos de dimensión finita sobre un campo, que son álgebras simples (no tienen ideales bilaterales no triviales, al igual que los campos) cuyo centro es exactamente el campo) son un análogo no conmutativo de los campos de extensión y son más restrictivos que los generales. extensiones de anillo. El hecho de que los cuaterniones sean el único CSA no trivial sobre los números reales (hasta la equivalencia) puede compararse con el hecho de que los números complejos son la única extensión de campo finito no trivial de los números reales.

Cotizaciones

Lo considero una falta de elegancia o una imperfección en los cuaterniones, o más bien en el estado en que se ha desplegado hasta ahora, siempre que se hace o parece necesario recurrir a x, y, z, etc.

—  William Rowan Hamilton (hacia 1848) ^[44]

Se dice que el tiempo tiene una sola dimensión y el espacio tiene tres dimensiones. ... El cuaternión matemático participa de ambos elementos; en lenguaje técnico se puede decir que es "tiempo más espacio", o "espacio más tiempo": y en este sentido tiene, o al menos implica una referencia a, cuatro dimensiones. ... Y cómo el Uno del Tiempo, del Espacio los Tres, Podrían estar ceñidos en la Cadena de Símbolos .

—  William Rowan Hamilton (hacia 1853) ^[45]

Los cuaterniones vinieron de Hamilton después de haber realizado su realmente buen trabajo; y, aunque maravillosamente ingeniosos, han sido un verdadero mal para quienes los han tocado de alguna manera, incluido el secretario Maxwell .

—  W. Thompson, Lord Kelvin (1892) ^[46]

De hecho, hubo un tiempo en el que, aunque reconocía la idoneidad del análisis vectorial en la teoría electromagnética (y en la física matemática en general), pensé que era más difícil de entender y aplicar que el análisis cartesiano. Pero eso fue antes de que me hubiera desprendido del viejo hombre del mar cuaterniónico que se sujetaba a mis hombros mientras leía el único tratado accesible sobre el tema: los Cuaterniones del profesor Tait. Pero más tarde me di cuenta de que, en lo que respecta al análisis vectorial que necesitaba, el cuaternión no sólo no era necesario, sino que era un mal positivo de magnitud nada despreciable; y que al evitarlo, el establecimiento del análisis vectorial se hizo bastante simple y su funcionamiento también se simplificó, y que podría armonizarse convenientemente con el trabajo cartesiano ordinario. No hay ni el fantasma de un cuaternión en ninguno de mis artículos (excepto en uno, para un propósito especial). El análisis vectorial que utilizo puede describirse como una abreviatura conveniente y sistemática del análisis cartesiano; o bien, como Cuaterniones sin los cuaterniones, ... Creo que una colegiala estadounidense definió "Cuaternión" como "una antigua ceremonia religiosa". Sin embargo, esto fue un completo error. Los antiguos, a diferencia del profesor Tait, no lo sabían ni adoraban a los Cuaterniones.

—Oliver  Heaviside (1893) ^[47]

Ni las matrices ni los cuaterniones ni los vectores ordinarios fueron desterrados de estos diez capítulos [adicionales]. Porque, a pesar del poder indiscutible del cálculo tensorial moderno, esos lenguajes matemáticos más antiguos continúan, en mi opinión, ofreciendo ventajas notorias en el restringido campo de la relatividad especial. Además, tanto en la ciencia como en la vida cotidiana, el dominio de más de un idioma también es valioso, ya que amplía nuestras opiniones, conduce a la crítica y protege contra la hipóstasis [fundamento débil] del asunto expresado. mediante palabras o símbolos matemáticos.

—  Ludwik Silberstein (1924) ^[48]

... los cuaterniones parecen exudar un aire de decadencia del siglo XIX, como una especie bastante fracasada en la lucha por la vida de las ideas matemáticas. Es cierto que los matemáticos todavía guardan un lugar cálido en sus corazones por las notables propiedades algebraicas de los cuaterniones pero, desgraciadamente, tal entusiasmo significa poco para el científico físico más testarudo.

—  Simon L. Altmann (1986) ^[49]

Ver también

• Conversión entre cuaterniones y ángulos de Euler  – Estrategia matemática
• Cuaternión dual  : álgebra octodimensional sobre números reales
• Número dual complejo  : álgebra tetradimensional sobre números realesPages displaying short descriptions of redirect targets
• Álgebra exterior  - Álgebra de un espacio vectorial
• Orden de los cuaterniones de Hurwitz  - Concepto en matemáticas
• Cuaternión hiperbólico  : mutación de cuaterniones donde los vectores unitarios cuadran a +1
• Esfera Lénárt  : esfera transparente de borrado en seco utilizada para enseñar geometría esférica
• Matrices de Pauli  : matrices importantes en la mecánica cuántica y el estudio del espín
• Colector cuaterniónico  – Concepto en geometría
• Matriz cuaterniónica  – Concepto en álgebra lineal
• Politopo cuaterniónico  – Concepto en geometría
• Espacio proyectivo cuaterniónico  – Concepto en matemáticas
• Rotaciones en el espacio euclidiano de 4 dimensiones  : grupo ortogonal especial
• Slerp  : interpolación lineal esférica en gráficos por computadora
• Cuaternión dividido  : álgebra asociativa de cuatro dimensiones sobre los reales
• Tesseract  : análogo cuatridimensional del cubo

Notas

1. Joachim Lambek escribió una visión más personal de los cuaterniones en 1995. Escribió en su ensayo Si Hamilton hubiera prevalecido: cuaterniones en física : "Mi propio interés como estudiante de posgrado surgió del inspirador libro de Silberstein". Concluyó afirmando: "Creo firmemente que los cuaterniones pueden proporcionar un atajo para los matemáticos puros que deseen familiarizarse con ciertos aspectos de la física teórica". Lambek, J. (1995). "Si Hamilton hubiera prevalecido: Cuaterniones en física". Matemáticas. Inteligencia . vol. 17, núm. 4. págs. 7-15. doi :10.1007/BF03024783.
2. Es importante señalar que la parte vectorial de un cuaternión es, en verdad, un vector "axial" o " pseudovector ", no un vector ordinario o "polar", como lo demostró formalmente Altmann (1986). ^[24] Un vector polar se puede representar en los cálculos (por ejemplo, para la rotación por una "transformación de similitud" de un cuaternión) por un cuaternión imaginario puro, sin pérdida de información, pero los dos no deben confundirse. El eje de un cuaternión de rotación "binario" (180°) corresponde en tal caso a la dirección del vector polar representado.
3. En comparación, los números reales tienen dimensión 1, los números complejos tienen dimensión 2 y los octoniones tienen dimensión 8. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {O} }$
4. ^[33] dio la identificación de las raíces cuadradas de menos uno en , pero se omitió con frecuencia en otros textos. Hacia 1971 la esfera fue incluida por Sam Perlis en su exposición de tres páginas incluida en Historical Topics in Algebra publicado por el Consejo Nacional de Profesores de Matemáticas . ^[34] Más recientemente, la esfera de raíces cuadradas de menos uno se describe en el libro Clifford Algebras and the Classical Groups (Cambridge, 1995) de Ian R. Porteous en la proposición 8.13. ^[35] ${\displaystyle \mathbb {H} }$
5. Los libros sobre matemáticas aplicadas, como Corke (2017) ^[38], a menudo usan notación diferente con φ  :=1/2θ — es decir, otra variable θ = 2 φ .

Referencias

1. "Sobre Cuaterniones; o sobre un nuevo sistema de imaginarios en álgebra". Carta a John T. Graves . 17 de octubre de 1843.
2. Rozenfelʹd, Boris Abramovich (1988). La historia de la geometría no euclidiana: Evolución del concepto de espacio geométrico. Saltador. pag. 385.ISBN _ 9780387964584.
3. Hamilton. Hodges y Smith. 1853. pág. 60. líneas de cociente de cuaterniones espacio-tiempo tridimensional
4. Hardy 1881. Ginn, Heath y compañía. 1881. pág. 32.ISBN _ 9781429701860.
5. Curtis, Morton L. (1984), Matrix Groups (2ª ed.), Nueva York: Springer-Verlag , p. 10, ISBN 978-0-387-96074-6
6. Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Esquemas de muestreo orientacional basados ​​en politopos de cuatro dimensiones". Simetría . 2 (3): 1423-1449. Código Bib : 2010 Símm....2.1423M. doi : 10.3390/sym2031423 .
7. Kunze, Karsten; Schaeben, Helmut (noviembre de 2004). "La distribución de Bingham de cuaterniones y su transformación esférica de radón en el análisis de textura". Geología Matemática . 36 (8): 917–943. doi :10.1023/B:MATG.0000048799.56445.59. S2CID  55009081.
8. Smith, Frank (Tony). "¿Por qué no sedenión?" . Consultado el 8 de junio de 2018 .
9. Véase Hazewinkel, Gubareni y Kirichenko 2004, p. 12
10. Conway y Smith 2003, pág. 9
11. Bradley, Robert E.; Sandifer, Charles Edward (2007). Leonhard Euler: vida, obra y legado. Elsevier. pag. 193.ISBN _ 978-0-444-52728-8.Mencionan la afirmación de Wilhelm Blaschke en 1959 de que "los cuaterniones fueron identificados por primera vez por L. Euler en una carta a Goldbach escrita el 4 de mayo de 1748", y comentan que "no tiene ningún sentido decir que Euler "identificó" los cuaterniones en esta carta... esta afirmación es absurda."
12. Pujol, J., "Hamilton, Rodrigues, Gauss, cuaterniones y rotaciones: una reevaluación histórica" ​​Comunicaciones en análisis matemático (2012), 13 (2), 1-14
13. Gauss, CF (1900). "Mutationen des Raumes [Transformaciones del espacio] (c. 1819)". En Martín Brendel (ed.). Carl Friedrich Gauss Werke [ Las obras de Carl Friedrich Gauss ]. vol. 8. artículo editado por el Prof. Stäckel de Kiel, Alemania. Göttingen, DE: Königlichen Gesellschaft der Wissenschaften [Real Sociedad de Ciencias]. págs. 357–361.
14. Hamilton, WR (1844). "Carta". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . vol. xxv. págs. 489–495.
15. Hamilton, señor WR (1866). Hamilton, NOSOTROS (ed.). Elementos de cuaterniones. Londres: Longmans, Green, & Co.
16. Shoemake, Ken (1985). "Animación de rotación con curvas de cuaterniones" (PDF) . Gráficos de computadora . 19 (3): 245–254. doi :10.1145/325165.325242.Presentado en SIGGRAPH '85.
17. Tomb Raider (1996) se cita a menudo como el primer juego de computadora del mercado masivo que utilizó cuaterniones para lograr rotaciones tridimensionales suaves. Véase, por ejemplo, Nick Bobick (julio de 1998). "Rotar objetos utilizando cuaterniones". Desarrollador de juegos .
18. McCarthy, JM (1990). Introducción a la cinemática teórica. Prensa del MIT. ISBN 978-0-262-13252-7.
19. Hurwitz, A. (1919), Vorlesungen über die Zahlentheorie der Quaternionen , Berlín: J. Springer, JFM  47.0106.01, sobre los cuaterniones de Hurwitz
20. Huerta, John (27 de septiembre de 2010). "Presentación de los cuaterniones" (PDF) . Archivado (PDF) desde el original el 21 de octubre de 2014 . Consultado el 8 de junio de 2018 .
21. Wood, Charlie (6 de septiembre de 2018). "Los números extraños que dieron origen al álgebra moderna". Blog de abstracciones . Revista Quanta.
22. Evas (1976, pág. 391)
23. "Matemáticas: transformaciones mediante cuaterniones". Espacio Euclidiano . Una rotación de q1 seguida de una rotación de q2 equivale a una sola rotación de q2 q1 . Note la inversión de orden, es decir, colocamos la primera rotación en el lado derecho de la multiplicación.
24. Altmann, SL Rotaciones, cuaterniones y grupos dobles . Cap. 12.
25. Hamilton, señor William Rowan (1866). "Artículo 285". Elementos de cuaterniones. Longmans, Green y compañía. pag. 310.
26. Resistente (1881). "Elementos de Cuaterniones". Ciencia . biblioteca.cornell.edu. 2 (75): 65. doi :10.1126/science.os-2.75.564. PMID  17819877.
27. "grupo cuaternión". Wolframalpha.com .
28. Gibbs, J. Willard; Wilson, Edwin Bidwell (1901). Análisis vectorial. Prensa de la Universidad de Yale. pag. 428. diádico tensor derecho
29. Hamilton, WR (1844–1850). "Sobre cuaterniones o un nuevo sistema de imaginarios en álgebra". Colección David R. Wilkins. Revista Filosófica . Trinity College de Dublín .
30. "Visualización de cuaterniones". Morgan-Kaufmann/Elsevier. 2005.
31. "[sin título citado; evaluación determinante]". Wolframalpha.com .
32. Hermano lejano, Richard William; Groß, Jürgen; Troschke, Sven-Oliver (2003). "Representación matricial de cuaterniones". Álgebra lineal y sus aplicaciones . 362 : 251–255. doi : 10.1016/s0024-3795(02)00535-9 .
33. Hamilton, WR (1899). Elementos de Cuaterniones (2ª ed.). Prensa de la Universidad de Cambridge. pag. 244.ISBN _ 1-108-00171-8.
34. Perlis, Sam (1971). "Cápsula 77: Cuaterniones". Temas históricos en álgebra . Temas Históricos para el Aula de Matemáticas. vol. 31. Reston, VA: Consejo Nacional de Profesores de Matemáticas . pag. 39.ISBN _ 9780873530583. OCLC  195566.
35. Porteous, Ian R. (1995). "Capítulo 8: Cuaterniones". Álgebras de Clifford y los grupos clásicos (PDF) . Estudios de Cambridge en Matemáticas Avanzadas. vol. 50. Cambridge: Prensa de la Universidad de Cambridge . pag. 60. doi :10.1017/CBO9780511470912.009. ISBN 9780521551779. SEÑOR  1369094. OCLC  32348823.
36. "[sin título citado]" (PDF) . bridgesmathart.org . archivo . Consultado el 19 de agosto de 2018 .
37. Särkkä, Simo (28 de junio de 2007). "Notas sobre cuaterniones" (PDF) . Lce.hut.fi. _ Archivado desde el original (PDF) el 5 de julio de 2017.
38. Corke, Peter (2017). Robótica, Visión y Control: Algoritmos fundamentales en MATLAB . Saltador . ISBN 978-3-319-54413-7.
39. Parque, FC; Ravani, Bahram (1997). "Interpolación invariante suave de rotaciones". Transacciones ACM sobre gráficos . 16 (3): 277–295. doi : 10.1145/256157.256160 . S2CID  6192031.
40. Hanson, Jason (2011). "Rotaciones en tres, cuatro y cinco dimensiones". arXiv : 1103.5263 [matemáticas.MG].
41. Günaşti, Gökmen (2016). Álgebra de cuaterniones, sus aplicaciones en rotaciones y más allá de los cuaterniones (BS). Universidad Linneo.
42. "Grupos de puntos tridimensionales". www.classe.cornell.edu . Consultado el 9 de diciembre de 2022 .
43. "Cuaterniones y álgebra geométrica". geometrialgebra.net . Consultado el 12 de septiembre de 2008 .Véanse también: Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007). Álgebra geométrica para informática. Morgan Kaufman . ISBN 978-0-12-369465-2.
44. Hamilton, William Rowan (1853). Conferencias sobre cuaterniones. Dublín: Hodges y Smith. pag. 522.
45. Graves, RP Vida de Sir William Rowan Hamilton. Dublín Hodges, Figgis. págs. 635–636.
46. Thompson, Silvanus Phillips (1910). La vida de William Thomson (Vol. 2). Londres, Macmillan. pag. 1138.
47. Heaviside, Oliver (1893). Teoría electromagnética. vol. I. Londres, Reino Unido: The Electrician Printing and Publishing Company. págs. 134-135.
48. Ludwik Silberstein (1924). Prefacio a la segunda edición de La Teoría de la Relatividad
49. Altmann, Simon L. (1986). Rotaciones, cuaterniones y grupos dobles . Prensa de Clarendon. ISBN 0-19-855372-2. LCCN  85013615.

Otras lecturas

Libros y publicaciones

• Hamilton, William Rowan (1844). "Sobre los cuaterniones, o sobre un nuevo sistema de imaginarios en álgebra". Revista Filosófica . 25 (3): 489–495. doi :10.1080/14786444408645047.
• Hamilton, William Rowan (1853), " Conferencias sobre cuaterniones ". Real Academia Irlandesa.
• Hamilton (1866) Elementos de Quaternions University of Dublin Press. Editado por William Edwin Hamilton, hijo del autor fallecido.
• Hamilton (1899) Elementos de Quaternions volumen I, (1901) volumen II. Editado por Charles Jasper Joly ; publicado por Longmans, Green & Co.
• Tait, Peter Guthrie (1873), " Un tratado elemental sobre cuaterniones ". 2ª ed., Cambridge, [inglés]: The University Press.
• Maxwell, James Clerk (1873), " Tratado sobre electricidad y magnetismo ". Prensa de Clarendon, Oxford.
• Tait, Peter Guthrie (1886), " "Copia archivada". Archivado desde el original el 8 de agosto de 2014. Consultado el 26 de junio de 2005 .{{cite web}}: CS1 maint: archived copy as title (link) CS1 maint: unfit URL (link)". MA Sec. RSE Encyclopædia Britannica , novena edición, 1886, vol. XX, págs. 160-164. ( archivo PostScript comprimido )
• Joly, Charles Jasper (1905). Un manual de cuaterniones . Macmillan. LCCN  05036137.
• Macfarlane, Alejandro (1906). Análisis de vectores y cuaterniones (4ª ed.). Wiley. LCCN  16000048.
• Chisholm, Hugh , ed. (1911). "Álgebra"  . Encyclopædia Britannica (11ª ed.). Prensa de la Universidad de Cambridge.( Ver sección sobre cuaterniones ) .
• Finkelstein, David; Jauch, Josef M.; Schiminovich, Samuel; Speiser, David (1962). "Fundamentos de la mecánica cuántica de cuaterniones". J. Matemáticas. Física . 3 (2): 207–220. Código bibliográfico : 1962JMP......3..207F. doi :10.1063/1.1703794. S2CID  121453456.
• Du Val, Patricio (1964). Homografías, cuaterniones y rotaciones . Monografías matemáticas de Oxford. Prensa de Clarendon. LCCN  64056979.
• Michael J. Crowe (1967), Una historia del análisis vectorial : la evolución de la idea de un sistema vectorial , University of Notre Dame Press. Examina los sistemas de vectores mayores y menores del siglo XIX (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside).
• Altmann, Simon L. (1989). "Hamilton, Rodrigues y el escándalo del Cuaternión". Revista Matemáticas . 62 (5): 291–308. doi :10.1080/0025570X.1989.11977459.
• Pujol, José (2014). "Sobre los primeros trabajos casi olvidados de Hamilton sobre la relación entre rotaciones y cuaterniones y sobre la composición de rotaciones". El Mensual Matemático Estadounidense . 121 (6): 515–522. doi : 10.4169/amer.math.monthly.121.06.515. S2CID  1543951.
• Adler, Stephen L. (1995). Mecánica cuántica cuaterniónica y campos cuánticos . Serie internacional de monografías sobre física. vol. 88. Prensa de la Universidad de Oxford. ISBN 0-19-506643-X. LCCN  94006306.
• Ward, JP (1997). Cuaterniones y números de Cayley: álgebra y aplicaciones . Académico Kluwer. ISBN 0-7923-4513-4.
• Kantor, Illinois; Solodnikov, AS (1989). Números hipercomplejos, una introducción elemental a las álgebras . Springer-Verlag. ISBN 0-387-96980-2.
• Gürlebeck, Klaus; Sprössig, Wolfgang (1997). Cálculo cuaterniónico y Clifford para físicos e ingenieros . Métodos matemáticos en la práctica. vol. 1. Wiley. ISBN 0-471-96200-7. LCCN  98169958.
• Kuipers, Jack (2002). Cuaterniones y secuencias de rotación: introducción con aplicaciones a órbitas, aeroespacial y realidad virtual . Prensa de la Universidad de Princeton . ISBN 0-691-10298-8.
• Conway, John Horton ; Smith, Derek A. (2003). Sobre cuaterniones y octoniones: su geometría, aritmética y simetría . AK Peters. ISBN 1-56881-134-9.(revisar).
• Jack, PM (2003). "El espacio físico como estructura de cuaternión, I: ecuaciones de Maxwell. Una breve nota". arXiv : math-ph/0307038 .
• Krávchenko, Vladislav (2003). Análisis cuaterniónico aplicado . Editorial Heldermann. ISBN 3-88538-228-8.
• Hazewinkel, Michiel ; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004). Álgebras, anillos y módulos. vol. 1. Saltador. ISBN 1-4020-2690-0.
• Hanson, Andrew J. (2006). Visualizando cuaterniones. Elsevier. ISBN 0-12-088400-3.
• Binz, Ernst; Vainas, Sonja (2008). "1. El campo sesgado de los cuaterniones". Geometría de los grupos de Heisenberg . Sociedad Matemática Estadounidense . ISBN 978-0-8218-4495-3.
• Doran, Chris JL ; Lasenby, Anthony N. (2003). Álgebra geométrica para físicos . Prensa de la Universidad de Cambridge. ISBN 978-0-521-48022-2.
• Vince, John A. (2008). Álgebra geométrica para gráficos por computadora . Saltador. ISBN 978-1-84628-996-5.
• Para moléculas que pueden considerarse cuerpos rígidos clásicos, la simulación por computadora de dinámica molecular emplea cuaterniones. Fueron introducidos por primera vez con este propósito por Evans, DJ (1977). "Sobre la representación del espacio de orientación". Mol. Física . 34 (2): 317–325. Código bibliográfico : 1977MolPh..34..317E. doi :10.1080/00268977700101751.
• Zhang, Fuzhen (1997). "Cuaterniones y matrices de cuaterniones". Álgebra lineal y sus aplicaciones . 251 : 21–57. doi : 10.1016/0024-3795(95)00543-9 .
• Ron Goldman (2010). Repensar los cuaterniones: teoría y computación . Morgan y Claypool. ISBN 978-1-60845-420-4.
• Eves, Howard (1976), Introducción a la historia de las matemáticas (4ª ed.), Nueva York: Holt, Rinehart y Winston , ISBN 0-03-089539-1
• Voight, John (2021). Álgebras de cuaterniones . Textos de Posgrado en Matemáticas. vol. 288. Saltador. doi : 10.1007/978-3-030-56694-4 . ISBN 978-3-030-57467-3.

Enlaces y monografías

• "Avisos de cuaterniones".Avisos y materiales relacionados con las presentaciones de la conferencia Quaternion.
• "Cuaternión", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• "Preguntas frecuentes". Matriz y Cuaternión . 1.21.
• Más dulce, Doug. "Hacer física con cuaterniones".
• Cuaterniones para mecánica y gráficos por computadora (Gernot Hoffman)
• Gsponer, André; Hurni, Jean-Pierre (2002). "La herencia física de Sir WR Hamilton". arXiv : math-ph/0201058 .
• Wilkins, DR "La investigación de Hamilton sobre los cuaterniones".
• Grossman, David J. "Cuaternión Julia Fractales".Fractales de Julia del cuaternión con trazado de rayos modelo 3d
• "Matemáticas y conversiones de cuaterniones".Gran página que explica matemáticas básicas con enlaces a fórmulas sencillas de conversión de rotación.
• Mathews, John H. "Bibliografía de cuaterniones". Archivado desde el original el 2 de septiembre de 2006.
• "Poderes del cuaternión". GameDev.net.
• Hanson, Andrés. "Visualización de la página de inicio de Quaternions". Archivado desde el original el 5 de noviembre de 2006.
• Karney, Charles FF (enero de 2007). "Cuaterniones en modelado molecular". J. Mol. Grafico. Modificación . 25 (5): 595–604. arXiv : física/0506177 . doi :10.1016/j.jmgm.2006.04.002. PMID  16777449. S2CID  6690718.
• Mebius, Johan E. (2005). "Una prueba basada en matrices del teorema de representación de cuaterniones para rotaciones de cuatro dimensiones". arXiv : matemáticas/0501249 .
• Mebius, Johan E. (2007). "Derivación de la fórmula de Euler-Rodrigues para rotaciones tridimensionales a partir de la fórmula general para rotaciones cuatridimensionales". arXiv : matemáticas/0701759 .
• "Paseo de Hamilton". Departamento de Matemáticas, NUI Maynooth .
• "Usando cuaterniones para representar la rotación". OpenGL:Tutoriales . Archivado desde el original el 15 de diciembre de 2007.
• David Erickson, Investigación y Desarrollo de Defensa de Canadá (DRDC), Derivación completa de la matriz de rotación a partir de la representación de cuaterniones unitarios en el artículo DRDC TR 2005-228.
• Martínez, Alberto. "Matemáticas negativas, cómo se pueden doblar positivamente las reglas matemáticas". Departamento de Historia, Universidad de Texas. Archivado desde el original el 24 de septiembre de 2011.
• Stahlke, D. "Cuaterniones en mecánica clásica" (PDF) .
• Morier-Genoud, Sophie; Ovsienko, Valentín (2008). "Bueno, papá, ¿puedes multiplicar trillizos?". arXiv : 0810.5562 [matemáticas.AC].describe cómo los cuaterniones se pueden convertir en un álgebra conmutativa sesgada graduada por Z /2 × Z /2 × Z /2 .
• Joyce, Helen (noviembre de 2004). "Cuaterniones curiosos". presentado por John Báez .
• Ibáñez, Luis. «Tutorial sobre Cuaterniones. Parte I» (PDF) . Archivado desde el original (PDF) el 4 de febrero de 2012 . Consultado el 5 de diciembre de 2011 .Parte II (PDF; usando la terminología de Hamilton, que difiere del uso moderno)
• Ghiloni, R.; Moretti, V.; Perotti, A. (2013). "Cálculo funcional de corte continuo en espacios cuaterniónicos de Hilbert". Rev. Matemáticas. Física . 25 (4): 1350006–126. arXiv : 1207.0666 . Código Bib : 2013RvMaP..2550006G. doi :10.1142/S0129055X13500062. S2CID  119651315.
  Ghiloni, R.; Moretti, V.; Perotti, A. (2017). "Representaciones espectrales de operadores normales mediante medidas valoradas de proyección cuaterniónica entrelazadas". Rev. Matemáticas. Física . 29 : 1750034. arXiv : 1602.02661 . doi :10.1142/S0129055X17500349. S2CID  124709652.dos artículos expositivos sobre cálculo funcional continuo y teoría espectral en espacios cuanterniónicos de Hilbert útiles en mecánica cuántica cuaterniónica rigurosa.
• Quaternions la aplicación de Android muestra el cuaternión correspondiente a la orientación del dispositivo.
• Artículo sobre rotación de objetos usando cuaterniones que habla sobre el uso de cuaterniones para la rotación en videojuegos/gráficos por computadora.

enlaces externos

• Medios relacionados con los cuaterniones en Wikimedia Commons
• Paulson, Lawrence C. Quaternions (Desarrollo de pruebas formales en Isabelle/HOL, Archivo de pruebas formales)
• Cuaterniones – Visualización