En gráficos por computadora , slerp es la abreviatura de interpolación lineal esférica , introducida por Ken Shoemake [1] en el contexto de la interpolación de cuaterniones con el propósito de animar la rotación 3D . Se refiere al movimiento a velocidad constante a lo largo de un arco de círculo máximo de radio unitario , dados los extremos y un parámetro de interpolación entre 0 y 1.
Slerp tiene una fórmula geométrica independiente de los cuaterniones e independiente de la dimensión del espacio en el que está incrustado el arco. Esta fórmula, una suma ponderada simétrica atribuida a Glenn Davis, se basa en el hecho de que cualquier punto de la curva debe ser una combinación lineal de los extremos. Sean p 0 y p 1 los puntos primero y último del arco, y sea t el parámetro, 0 ≤ t ≤ 1 . Calcule Ω como el ángulo subtendido por el arco, de modo que cos Ω = p 0 ⋅ p 1 , el producto escalar n -dimensional de los vectores unitarios desde el origen hasta los extremos. La fórmula geométrica es entonces
La simetría radica en el hecho de que slerp( p 0 , p 1 ; t ) = slerp( p 1 , p 0 ; 1 − t ) . En el límite cuando Ω → 0 , esta fórmula se reduce a la fórmula simétrica correspondiente para la interpolación lineal ,
Una trayectoria slerp es, de hecho, el equivalente geométrico esférico de una trayectoria a lo largo de un segmento de línea en el plano; un círculo máximo es una geodésica esférica .
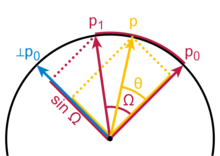
Más familiar que la fórmula general de slerp es el caso en el que los vectores finales son perpendiculares, en cuyo caso la fórmula es p 0 cos θ + p 1 sen θ . Si θ = t π /2 , y aplicamos la identidad trigonométrica cos θ = sen( π /2 − θ ) , obtenemos la fórmula de slerp. El factor de 1/sen Ω en la fórmula general es una normalización, ya que un vector p 1 en un ángulo de Ω con respecto a p 0 se proyecta sobre la perpendicular ⊥ p 0 con una longitud de solo sen Ω .
Algunos casos especiales de slerp admiten un cálculo más eficiente. Cuando se debe dibujar un arco circular en una imagen rasterizada, el método preferido es alguna variación del algoritmo del círculo de Bresenham . La evaluación en los valores de parámetros especiales 0 y 1 da como resultado, de manera trivial, p 0 y p 1 , respectivamente; y la bisección, la evaluación en 1/2 , se simplifica a ( p 0 + p 1 )/2 , normalizado. Otro caso especial, común en animación, es la evaluación con extremos fijos y pasos paramétricos iguales. Si p k −1 y p k son dos valores consecutivos, y si c es el doble de su producto escalar (constante para todos los pasos), entonces el siguiente valor, p k +1 , es la reflexión p k +1 = cp k − p k −1 .
Cuando se aplica slerp a los cuaterniones unitarios , la ruta del cuaternión se asigna a una ruta a través de rotaciones 3D de una manera estándar . El efecto es una rotación con velocidad angular uniforme alrededor de un eje de rotación fijo . Cuando el punto final inicial es el cuaternión identidad, slerp da un segmento de un subgrupo de un parámetro tanto del grupo de Lie de rotaciones 3D, SO(3) , como de su grupo de cobertura universal de cuaterniones unitarios, S 3 . Slerp da una ruta más recta y más corta entre sus puntos finales del cuaternión, y se asigna a una rotación a través de un ángulo de 2Ω. Sin embargo, debido a que la cobertura es doble ( q y − q se asignan a la misma rotación), la ruta de rotación puede girar en el "camino corto" (menos de 180°) o en el "camino largo" (más de 180°). Los caminos largos se pueden evitar negando un extremo si el producto escalar, cos Ω , es negativo, garantizando así que −90° ≤ Ω ≤ 90° .
Slerp también tiene expresiones en términos del álgebra de cuaterniones, todas usando exponenciación . Las potencias reales de un cuaternión se definen en términos de la función exponencial del cuaternión , escrita como e q y dada por la serie de potencias igualmente familiar del cálculo, el análisis complejo y el álgebra matricial:
Escribiendo un cuaternión unitario q en forma versor , cos Ω + v sen Ω , con v un 3-vector unitario, y notando que el cuadrado del cuaternión v 2 es igual a −1 (lo que implica una versión cuaternial de la fórmula de Euler ), tenemos e v Ω = q , y q t = cos t Ω + v sen t Ω . La identificación de interés es q = q 1 q 0 −1 , de modo que la parte real de q es cos Ω , lo mismo que el producto escalar geométrico usado anteriormente. Aquí hay cuatro expresiones de cuaternión equivalentes para slerp.
La derivada de slerp( q 0 , q 1 ; t ) con respecto a t , suponiendo que los extremos son fijos, es log( q 1 q 0 −1 ) multiplicado por el valor de la función, donde el logaritmo natural del cuaternión en este caso da como resultado la mitad del vector de velocidad angular 3D . El vector tangente inicial se transporta en paralelo a cada tangente a lo largo de la curva; por lo tanto, la curva es, de hecho, una geodésica.
En el espacio tangente de cualquier punto de una curva de Slerp de cuaternión, la inversa de la función exponencial transforma la curva en un segmento de línea. Las curvas de Slerp que no pasan por un punto no se transforman en líneas en el espacio tangente de ese punto.
Los slerps de cuaternión se utilizan comúnmente para construir curvas de animación suaves imitando construcciones afines como el algoritmo de De Casteljau para curvas de Bézier . Dado que la esfera no es un espacio afín , las propiedades familiares de las construcciones afines pueden fallar, aunque las curvas construidas pueden ser completamente satisfactorias. Por ejemplo, el algoritmo de De Casteljau se puede utilizar para dividir una curva en un espacio afín; esto no funciona en una esfera.
El slerp de dos valores se puede extender para interpolar entre muchos cuaterniones unitarios, [2] pero la extensión pierde el tiempo de ejecución fijo del algoritmo slerp.
![{\displaystyle \operatorname {slerp} (p_{0},p_{1};t)={\frac {\sin {[(1-t)\Omega }]}{\sin \Omega }}p_{0}+{\frac {\sin[t\Omega ]}{\sin \Omega }}p_{1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06566aaf6dd1792a43456d6cbdf31054f731e745)
![{\displaystyle {\begin{aligned}\operatorname {slerp} (q_{0},q_{1},t)&=q_{0}(q_{0}^{-1}q_{1})^{t}\\[6pt]&=q_{1}(q_{1}^{-1}q_{0})^{1-t}\\[6pt]&=(q_{0}q_{1}^{-1})^{1-t}q_{1}\\[6pt]&=(q_{1}q_{0}^{-1})^{t}q_{0}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e28b6824e549921d9bd4403639c1eef992dd9f)