Función (matemáticas)

En matemáticas , una función de un conjunto $X$ a un conjunto $Y$ asigna a cada elemento de $X$ exactamente un elemento de $Y.$ ^[1] El conjunto $X$ se denomina dominio de la función ^[2] y el conjunto $Y$ se denomina codominio de la función. [ ^3]

Las funciones fueron originalmente la idealización de cómo una cantidad variable depende de otra cantidad. Por ejemplo, la posición de un planeta es una función del tiempo. Históricamente , el concepto fue elaborado con el cálculo infinitesimal a finales del siglo XVII, y, hasta el siglo XIX, las funciones que se consideraban eran diferenciables (es decir, tenían un alto grado de regularidad). El concepto de función se formalizó a finales del siglo XIX en términos de la teoría de conjuntos , y esto aumentó enormemente las posibles aplicaciones del concepto.

Una función se denota a menudo por una letra como $f$ , $g$ o $h$ . El valor de una función $f$ en un elemento $x$ de su dominio (es decir, el elemento del codominio que está asociado con $x$ ) se denota por $f (x)$ ; por ejemplo, el valor de $f$ en $x = 4$ se denota por $f (4)$ . Comúnmente, una función específica se define por medio de una expresión que depende de $x$ , como en este caso, algún cálculo, llamado $f(x)=x^{2}+1;$ La evaluación de funciones puede ser necesaria para deducir el valor de la función en un valor particular; por ejemplo, sientonces $f(x)=x^{2}+1,$ $f(4)=4^{2}+1=17.$

Dado su dominio y su codominio, una función está representada de forma única por el conjunto de todos los pares $(x, f (x))$ , llamado gráfico de la función , un medio popular para ilustrar la función. ^{[nota 1]}^[4] Cuando el dominio y el codominio son conjuntos de números reales, cada uno de estos pares puede considerarse como las coordenadas cartesianas de un punto en el plano.

Las funciones se utilizan ampliamente en la ciencia , la ingeniería y en la mayoría de los campos de las matemáticas. Se ha dicho que las funciones son "los objetos centrales de investigación" en la mayoría de los campos de las matemáticas. ^[5]

El concepto de función ha evolucionado significativamente a lo largo de los siglos, desde sus orígenes informales en las matemáticas antiguas hasta su formalización en el siglo XIX. Consulte Historia del concepto de función para obtener más detalles.

Definición

Una función $f$ de un conjunto $X$ a un conjunto $Y$ es una asignación de un elemento de $Y$ a cada elemento de $X.$ El conjunto $X$ se denomina dominio de la función y el conjunto $Y$ se denomina codominio de la función.

Si el elemento $y$ en $Y$ se asigna a $x$ en $X$ por la función $f$ , se dice que $f$ asigna $x$ a $y$ , y esto se escribe comúnmente En esta notación, $x$ es el argumento o variable de la función. Un elemento específico $x$ de $X$ es un valor de la variable , y el elemento correspondiente de $Y$ es el valor de la función en $x$ , o la imagen de $x$ bajo la función. $y=f(x).$

Una función $f$ , su dominio $X$ y su codominio $Y$ se especifican a menudo mediante la notación Se puede escribir en lugar de , donde el símbolo (que se lee ' mapea a ') se usa para especificar dónde se mapea un elemento particular $x$ en el dominio mediante $f$ . Esto permite la definición de una función sin nombrarla. Por ejemplo, la función cuadrada es la función $f:X\to Y.$ $x\mapsto y$ $y=f(x)$ $\mapsto$ $x\mapsto x^{2}.$

El dominio y el codominio no siempre se dan explícitamente cuando se define una función. En particular, es común que uno solo pueda saber, sin algún cálculo (posiblemente difícil), que el dominio de una función específica está contenido en un conjunto más grande. Por ejemplo, si es una función real , la determinación del dominio de la función requiere conocer los ceros de $f.$ Esta es una de las razones por las que, en análisis matemático , "una función de $X$ a $Y$ " puede referirse a una función que tiene un subconjunto propio de $X$ como dominio. ^{[nota 2]} Por ejemplo, una "función de los números reales a los reales" puede referirse a una función de valor real de una variable real cuyo dominio es un subconjunto propio de los números reales , típicamente un subconjunto que contiene un intervalo abierto no vacío . Tal función se llama entonces función parcial . $f:\mathbb {R} \to \mathbb {R}$ $x\mapsto 1/f(x)$

El rango o imagen de una función es el conjunto de las imágenes de todos los elementos del dominio. ^[6]^[7]^[8]^[9]

Una función $f$ en un conjunto $S$ significa una función del dominio $S$ , sin especificar codominio. Sin embargo, algunos autores la utilizan como forma abreviada de decir que la función es $f : S \to S$ .

Definición formal

La definición anterior de una función es esencialmente la de los fundadores del cálculo , Leibniz , Newton y Euler . Sin embargo, no se puede formalizar , ya que no existe una definición matemática de una "asignación". Recién a fines del siglo XIX se pudo proporcionar la primera definición formal de una función, en términos de la teoría de conjuntos . Esta definición de teoría de conjuntos se basa en el hecho de que una función establece una relación entre los elementos del dominio y algunos (posiblemente todos) elementos del codominio. Matemáticamente, una relación binaria entre dos conjuntos $X$ e $Y$ es un subconjunto del conjunto de todos los pares ordenados tales que y El conjunto de todos estos pares se llama producto cartesiano de $X$ e $Y$ y se denota Por lo tanto, la definición anterior se puede formalizar de la siguiente manera. $(x,y)$ $x\in X$ $y\in Y.$ $X\times Y.$

Una función con dominio $X$ y codominio $Y$ es una relación binaria $R$ entre $X$ e $Y$ que satisface las dos condiciones siguientes: ^[10]

Porque todo lo que hay ahí existe de tal manera que $x$ $X$ $y$ $Y$ $(x,y)\in R.$
Si y entonces $(x,y)\in R$ $(x,z)\in R,$ $y=z.$

Esta definición se puede reescribir de manera más formal, sin hacer referencia explícita al concepto de relación, pero utilizando más notación (incluida la notación de generador de conjuntos ):

Una función está formada por tres conjuntos, el dominio, el codominio y el grafo que satisfacen las tres condiciones siguientes. $X,$ $Y,$ $R$

$R\subseteq \{(x,y)\mid x\in X,y\in Y\}$
$\forall x\in X,\exists y\in Y,\left(x,y\right)\in R\qquad$
$(x,y)\in R\land (x,z)\in R\implies y=z\qquad$

Funciones parciales

Las funciones parciales se definen de manera similar a las funciones ordinarias, con la condición "total" eliminada. Es decir, una función parcial de $X$ a $Y$ es una relación binaria $R$ entre $X$ e $Y$ tal que, para cada hay como máximo un $y$ en $Y$ tal que $x\in X,$ $(x,y)\in R.$

Usando notación funcional, esto significa que, dado que está en $Y$ , o no está definido. $x\in X,$ $f(x)$

El conjunto de los elementos de $X$ tal que está definido y pertenece a $Y$ se llama dominio de definición de la función. Una función parcial de $X$ a $Y$ es, por tanto, una función ordinaria que tiene como dominio un subconjunto de $X$ llamado dominio de definición de la función. Si el dominio de definición es igual $a X$ , se suele decir que la función parcial es una función total . $f(x)$

En varias áreas de las matemáticas, el término "función" se refiere a funciones parciales y no a funciones ordinarias. Esto suele suceder cuando las funciones se especifican de una manera que hace difícil o incluso imposible determinar su dominio.

En cálculo , una función de valor real de una variable real o función real es una función parcial del conjunto de los números reales a sí misma. Dada una función real, su inverso multiplicativo también es una función real. La determinación del dominio de definición de un inverso multiplicativo de una función (parcial) equivale a calcular los ceros de la función, los valores en los que la función está definida pero no su inverso multiplicativo. $\mathbb {R}$ $f:x\mapsto f(x)$ $x\mapsto 1/f(x)$

De manera similar, una función de variable compleja es generalmente una función parcial con un dominio de definición incluido en el conjunto de los números complejos . La dificultad de determinar el dominio de definición de una función compleja se ilustra con la inversa multiplicativa de la función zeta de Riemann : la determinación del dominio de definición de la función es más o menos equivalente a la prueba o refutación de uno de los principales problemas abiertos en matemáticas, la hipótesis de Riemann . $\mathbb {C}$ $z\mapsto 1/\zeta (z)$

En la teoría de la computabilidad , una función recursiva general es una función parcial de los números enteros a los números enteros cuyos valores pueden calcularse mediante un algoritmo (en términos generales). El dominio de definición de dicha función es el conjunto de entradas para las que el algoritmo no se ejecuta indefinidamente. Un teorema fundamental de la teoría de la computabilidad es que no puede existir un algoritmo que tome una función recursiva general arbitraria como entrada y compruebe si $0$ pertenece a su dominio de definición (véase el problema de la detención ).

Funciones multivariadas

Una función multivariable , función multivariable o función de varias variables es una función que depende de varios argumentos. Este tipo de funciones son muy comunes. Por ejemplo, la posición de un automóvil en una carretera es una función del tiempo de recorrido y de su velocidad media.

Formalmente, una función de $n$ variables es una función cuyo dominio es un conjunto de $n$ -tuplas. ^{[nota 3]} Por ejemplo, la multiplicación de números enteros es una función de dos variables, o función bivariada , cuyo dominio es el conjunto de todos los pares ordenados (2-tuplas) de números enteros, y cuyo codominio es el conjunto de números enteros. Lo mismo es cierto para cada operación binaria . Comúnmente, una $n$ -tupla se denota encerrada entre paréntesis, como en Cuando se usa la notación funcional , uno usualmente omite los paréntesis que rodean las tuplas, escribiendo en lugar de $(1,2,\ldots ,n).$ $f(x_{1},\ldots ,x_{n})$ $f((x_{1},\ldots ,x_{n})).$

Dados $n$ conjuntos, el conjunto de todas $las n$ -tuplas tales que se denomina producto cartesiano de y se denota $X_{1},\ldots ,X_{n},$ $(x_{1},\ldots ,x_{n})$ $x_{1}\in X_{1},\ldots ,x_{n}\in X_{n}$ $X_{1},\ldots ,X_{n},$ $X_{1}\times \cdots \times X_{n}.$

Por lo tanto, una función multivariada es una función que tiene como dominio un producto cartesiano o un subconjunto propio de un producto cartesiano.

f:U\to Y,

donde el dominio $U$ tiene la forma

U\subseteq X_{1}\times \cdots \times X_{n}.

Si todos los son iguales al conjunto de los números reales o al conjunto de los números complejos , se habla respectivamente de una función de varias variables reales o de una función de varias variables complejas . $X_{i}$ $\mathbb {R}$ $\mathbb {C}$

Notación

Existen varias formas estándar de representar funciones. La notación más utilizada es la notación funcional, que es la primera notación que se describe a continuación.

Notación funcional

La notación funcional requiere que se le asigne un nombre a la función, que, en el caso de una función no especificada, suele ser la letra $f$ . Luego, la aplicación de la función a un argumento se denota por su nombre seguido de su argumento (o, en el caso de una función multivariable, sus argumentos) encerrado entre paréntesis, como en

f(x),\quad \sin(3),\quad {\text{or}}\quad f(x^{2}+1).

El argumento entre los paréntesis puede ser una variable , a menudo $x$ , que representa un elemento arbitrario del dominio de la función, un elemento específico del dominio ( $3$ en el ejemplo anterior) o una expresión que puede evaluarse como un elemento del dominio ( en el ejemplo anterior). El uso de una variable no especificada entre paréntesis es útil para definir una función explícitamente, como en "let ". $x^{2}+1$ $f(x)=\sin(x^{2}+1)$

Cuando el símbolo que denota la función consta de varios caracteres y no puede surgir ninguna ambigüedad, se pueden omitir los paréntesis de la notación funcional. Por ejemplo, es habitual escribir $sen x$ en lugar de $sen(x)$ .

La notación funcional fue utilizada por primera vez por Leonhard Euler en 1734. ^[11] Algunas funciones ampliamente utilizadas se representan mediante un símbolo que consta de varias letras (normalmente dos o tres, generalmente una abreviatura de su nombre). En este caso, se suele utilizar un tipo de letra romana , como " $sin$ " para la función seno , en contraste con la fuente itálica para símbolos de una sola letra.

La notación funcional se utiliza a menudo de manera coloquial para referirse a una función y, al mismo tiempo, nombrar su argumento, como en "sea una función". Esto es un abuso de la notación que resulta útil para una formulación más simple. $f(x)$

Notación de flecha

La notación de flecha define la regla de una función en línea, sin necesidad de que se le asigne un nombre a la función. Utiliza el símbolo de flecha ↦, que se pronuncia " maps to ". Por ejemplo, es la función que toma un número real como entrada y genera ese número más 1. Nuevamente, se implica un dominio y codominio de . $x\mapsto x+1$ $\mathbb {R}$

El dominio y el codominio también se pueden indicar explícitamente, por ejemplo:

{\begin{aligned}\operatorname {sqr} \colon \mathbb {Z} &\to \mathbb {Z} \\x&\mapsto x^{2}.\end{aligned}}

Esto define una función $sqr$ de los números enteros a los números enteros que devuelve el cuadrado de su entrada.

Como aplicación común de la notación de flechas, supongamos que es una función en dos variables y queremos hacer referencia a una función parcialmente aplicada producida al fijar el segundo argumento al valor $t$ $0$ sin introducir un nuevo nombre de función. La función en cuestión podría denotarse utilizando la notación de flechas. La expresión (léase: "la función que toma $x$ hasta $f$ de $x$ coma $t$ cero") representa esta nueva función con un solo argumento, mientras que la expresión $f$ $($ $x$ $0$ $,$ $t$ $0$ $)$ se refiere al valor de la función $f$ en el punto $($ $x$ $0$ $,$ $t$ $0$ $)$ . $f:X\times X\to Y;\;(x,t)\mapsto f(x,t)$ $X\to Y$ $x\mapsto f(x,t_{0})$ $x\mapsto f(x,t_{0})$

Notación de índice

Se puede utilizar la notación de índice en lugar de la notación funcional. Es decir, en lugar de escribir $f (x)$ , se escribe $f_{x}.$

Este suele ser el caso de las funciones cuyo dominio es el conjunto de los números naturales . Dicha función se denomina sucesión y, en este caso, el elemento se denomina $n-$ ésimo elemento de la sucesión. $f_{n}$

La notación de índice también se puede utilizar para distinguir algunas variables llamadas parámetros de las "variables verdaderas". De hecho, los parámetros son variables específicas que se consideran fijas durante el estudio de un problema. Por ejemplo, el mapa (ver arriba) se denotaría utilizando la notación de índice, si definimos la colección de mapas por la fórmula para todos los . $x\mapsto f(x,t)$ $f_{t}$ $f_{t}$ $f_{t}(x)=f(x,t)$ $x,t\in X$

Notación de puntos

En la notación, el símbolo $x$ no representa ningún valor; es simplemente un marcador de posición , lo que significa que, si $x$ se reemplaza por cualquier valor a la izquierda de la flecha, debe reemplazarse por el mismo valor a la derecha de la flecha. Por lo tanto, $x$ puede reemplazarse por cualquier símbolo, a menudo un punto intermedio " $\cdot$ ". Esto puede ser útil para distinguir la función $f$ $(\cdot)$ de su valor $f$ $($ $x$ $)$ en $x$ . $x\mapsto f(x),$

Por ejemplo, puede representar la función y puede representar una función definida por una integral con límite superior variable: . $a(\cdot )^{2}$ $x\mapsto ax^{2}$ ${\textstyle \int _{a}^{\,(\cdot )}f(u)\,du}$ ${\textstyle x\mapsto \int _{a}^{x}f(u)\,du}$

Notaciones especializadas

Existen otras notaciones especializadas para funciones en subdisciplinas de las matemáticas. Por ejemplo, en álgebra lineal y análisis funcional , las formas lineales y los vectores sobre los que actúan se denotan utilizando un par dual para mostrar la dualidad subyacente . Esto es similar al uso de la notación bra-ket en mecánica cuántica. En lógica y teoría de la computación , la notación de función del cálculo lambda se utiliza para expresar explícitamente las nociones básicas de abstracción y aplicación de funciones . En teoría de categorías y álgebra homológica , las redes de funciones se describen en términos de cómo ellas y sus composiciones conmutan entre sí utilizando diagramas conmutativos que extienden y generalizan la notación de flechas para funciones descritas anteriormente.

Funciones de más de una variable

En algunos casos, el argumento de una función puede ser un par ordenado de elementos tomados de uno o varios conjuntos. Por ejemplo, una función $f$ puede definirse como la que asigna cualquier par de números reales a la suma de sus cuadrados, . Este tipo de función se escribe comúnmente como "una función de dos variables" y se denomina así. Del mismo modo, se puede tener una función de tres o más variables, con notaciones como , . $(x,y)$ $x^{2}+y^{2}$ $f(x,y)=x^{2}+y^{2}$ $f(w,x,y)$ $f(w,x,y,z)$

Otros términos

Una función también puede denominarse mapa o aplicación , pero algunos autores distinguen entre el término "mapa" y "función". Por ejemplo, el término "mapa" suele reservarse para una "función" con algún tipo de estructura especial (p. ej., mapas de variedades ). En particular, se puede utilizar mapa en lugar de homomorfismo por razones de brevedad (p. ej., mapa lineal o mapa de $G$ a $H$ en lugar de homomorfismo de grupo de $G$ a $H$ ). Algunos autores ^[14] reservan la palabra aplicación para el caso en el que la estructura del codominio pertenece explícitamente a la definición de la función.

Algunos autores, como Serge Lang , ^[13] utilizan "función" sólo para referirse a mapas para los cuales el codominio es un subconjunto de los números reales o complejos , y utilizan el término mapeo para funciones más generales.

En la teoría de sistemas dinámicos , una función denota una función de evolución utilizada para crear sistemas dinámicos discretos . Véase también la función de Poincaré .

Cualquiera sea la definición de mapa que se utilice, términos relacionados como dominio , codominio , inyectivo y continuo tienen el mismo significado que para una función.

Especificación de una función

Dada una función , por definición, a cada elemento del dominio de la función , hay un único elemento asociado a ella, el valor de en . Hay varias maneras de especificar o describir cómo se relaciona con , tanto explícitamente como implícitamente. A veces, un teorema o un axioma afirma la existencia de una función que tiene algunas propiedades, sin describirla con mayor precisión. A menudo, la especificación o descripción se denomina definición de la función . $f$ $x$ $f$ $f(x)$ $f$ $x$ $x$ $f(x)$ $f$

Enumerando los valores de las funciones

En un conjunto finito, una función puede definirse enumerando los elementos del codominio que están asociados a los elementos del dominio. Por ejemplo, si , entonces se puede definir una función mediante $A=\{1,2,3\}$ $f:A\to \mathbb {R}$ $f(1)=2,f(2)=3,f(3)=4.$

Por una fórmula

Las funciones suelen definirse mediante una expresión que describe una combinación de operaciones aritméticas y funciones definidas previamente; una fórmula de este tipo permite calcular el valor de la función a partir del valor de cualquier elemento del dominio. Por ejemplo, en el ejemplo anterior, se puede definir mediante la fórmula , para . $f$ $f(n)=n+1$ $n\in \{1,2,3\}$

Cuando una función se define de esta manera, la determinación de su dominio a veces es difícil. Si la fórmula que define la función contiene divisiones, los valores de la variable para los cuales un denominador es cero deben excluirse del dominio; por lo tanto, para una función complicada, la determinación del dominio pasa por el cálculo de los ceros de las funciones auxiliares. De manera similar, si en la definición de una función aparecen raíces cuadradas de a , el dominio se incluye en el conjunto de los valores de la variable para los cuales los argumentos de las raíces cuadradas son no negativos. $\mathbb {R}$ $\mathbb {R} ,$

Por ejemplo, define una función cuyo dominio es porque siempre es positivo si $x$ es un número real. Por otra parte, define una función de los números reales a los reales cuyo dominio se reduce al intervalo $[-1, 1]$ . (En textos antiguos, dicho dominio se denominaba dominio de definición de la función). $f(x)={\sqrt {1+x^{2}}}$ $f:\mathbb {R} \to \mathbb {R}$ $\mathbb {R} ,$ $1+x^{2}$ $f(x)={\sqrt {1-x^{2}}}$

Las funciones se pueden clasificar según la naturaleza de las fórmulas que las definen:

Una función cuadrática es una función que puede escribirse donde $a$ $,$ $b$ $,$ $c$ son constantes . $f(x)=ax^{2}+bx+c,$
En términos más generales, una función polinómica es una función que se puede definir mediante una fórmula que implica únicamente sumas, restas, multiplicaciones y exponenciación a potencias enteras no negativas. Por ejemplo, y son funciones polinómicas de . $f(x)=x^{3}-3x-1$ $f(x)=(x-1)(x^{3}+1)+2x^{2}-1$ $x$
Una función racional es la misma, permitiéndose también divisiones, como y $f(x)={\frac {x-1}{x+1}},$ $f(x)={\frac {1}{x+1}}+{\frac {3}{x}}-{\frac {2}{x-1}}.$
Una función algebraica es la misma, permitiéndose también raíces n -ésimas y raíces de polinomios .
Una función elemental ^{[nota 4]} es la misma, permitiéndose logaritmos y funciones exponenciales .

Funciones inversas e implícitas

Una función con dominio $X$ y codominio $Y$ , es biyectiva , si para cada $y$ en $Y$ , hay un y solo un elemento $x$ en $X$ tal que $y$ $=$ $f$ $($ $x$ $)$ . En este caso, la función inversa de $f$ es la función que mapea al elemento tal que $y$ $=$ $f$ $($ $x$ $)$ . Por ejemplo, el logaritmo natural es una función biyectiva de los números reales positivos a los números reales. Por lo tanto, tiene una inversa, llamada función exponencial , que mapea los números reales sobre los números positivos. $f:X\to Y,$ $f^{-1}:Y\to X$ $y\in Y$ $x\in X$

Si una función no es biyectiva, puede ocurrir que se puedan seleccionar subconjuntos y tales que la restricción de $f$ a $E$ sea una biyección de $E$ a $F$ , y tenga por tanto una inversa. Las funciones trigonométricas inversas se definen de esta manera. Por ejemplo, la función coseno induce, por restricción, una biyección del intervalo $[0,$ $π$ $]$ al intervalo $[-1, 1]$ , y su función inversa, llamada arcocoseno , mapea $[-1, 1]$ a $[0,$ $π$ $]$ . Las otras funciones trigonométricas inversas se definen de forma similar. $f:X\to Y$ $E\subseteq X$ $F\subseteq Y$

De manera más general, dada una relación binaria $R$ entre dos conjuntos $X$ e $Y$ , sea $E$ un subconjunto de $X$ tal que, para cada uno, existe algún conjunto tal que $x R y$ . Si se tiene un criterio que permita seleccionar un conjunto tal que $y$ para cada uno , esto define una función llamada función implícita , porque está definida implícitamente por la relación $R$ . $x\in E,$ $y\in Y$ $x\in E,$ $f:E\to Y,$

Por ejemplo, la ecuación del círculo unitario define una relación entre números reales. Si $-1 <$ $x$ $< 1$ hay dos valores posibles de $y$ , uno positivo y otro negativo. Para $x$ $= \pm 1$ , estos dos valores se vuelven iguales a 0. De lo contrario, no hay ningún valor posible de $y$ . Esto significa que la ecuación define dos funciones implícitas con dominio $[-1, 1]$ y codominios respectivos $[0, +\infty)$ y $(-\infty, 0]$ . $x^{2}+y^{2}=1$

En este ejemplo, la ecuación se puede resolver en $y$ , dando , pero, en ejemplos más complicados, esto es imposible. Por ejemplo, la relación define $y$ como una función implícita de $x$ , llamada el radical de Bring , que tiene como dominio y rango. El radical de Bring no se puede expresar en términos de las cuatro operaciones aritméticas y las raíces n ésimas . $y=\pm {\sqrt {1-x^{2}}},$ $y^{5}+y+x=0$ $\mathbb {R}$

El teorema de la función implícita proporciona condiciones de diferenciabilidad suaves para la existencia y unicidad de una función implícita en la vecindad de un punto.

Utilizando el cálculo diferencial

Muchas funciones pueden definirse como la antiderivada de otra función. Este es el caso del logaritmo natural , que es la antiderivada de $1/ x$ que es 0 para $x = 1.$ Otro ejemplo común es la función de error .

En términos más generales, muchas funciones, incluidas la mayoría de las funciones especiales , pueden definirse como soluciones de ecuaciones diferenciales . El ejemplo más simple es probablemente la función exponencial , que puede definirse como la única función que es igual a su derivada y toma el valor 1 para $x = 0$ .

Las series de potencias se pueden utilizar para definir funciones en el dominio en el que convergen. Por ejemplo, la función exponencial está dada por . Sin embargo, como los coeficientes de una serie son bastante arbitrarios, una función que es la suma de una serie convergente generalmente se define de otra manera, y la secuencia de los coeficientes es el resultado de algún cálculo basado en otra definición. Luego, la serie de potencias se puede utilizar para ampliar el dominio de la función. Por lo general, si una función para una variable real es la suma de su serie de Taylor en algún intervalo, esta serie de potencias permite ampliar inmediatamente el dominio a un subconjunto de los números complejos , el disco de convergencia de la serie. Luego, la continuación analítica permite ampliar aún más el dominio para incluir casi todo el plano complejo . Este proceso es el método que generalmente se utiliza para definir las funciones logarítmica , exponencial y trigonométrica de un número complejo. ${\textstyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}}$

Por recurrencia

Las funciones cuyo dominio son los números enteros no negativos, conocidas como secuencias , a veces se definen mediante relaciones de recurrencia .

La función factorial sobre los números enteros no negativos ( ) es un ejemplo básico, ya que puede definirse mediante la relación de recurrencia $n\mapsto n!$

n!=n(n-1)!\quad {\text{for}}\quad n>0,

y la condición inicial

0!=1.

Representando una función

Un gráfico se utiliza habitualmente para dar una imagen intuitiva de una función. Como ejemplo de cómo un gráfico ayuda a comprender una función, es fácil ver a partir de su gráfico si una función es creciente o decreciente. Algunas funciones también pueden representarse mediante gráficos de barras .

Gráficos y diagramas

Dada una función su gráfica es, formalmente, el conjunto $f:X\to Y,$

G=\{(x,f(x))\mid x\in X\}.

En el caso frecuente en que $X$ e $Y$ son subconjuntos de los números reales (o pueden identificarse con dichos subconjuntos, p. ej. intervalos ), un elemento puede identificarse con un punto que tiene coordenadas $x$ $,$ $y$ en un sistema de coordenadas bidimensional, p. ej. el plano cartesiano . Partes de esto pueden crear un gráfico que representa (partes de) la función. El uso de gráficos es tan omnipresente que también se les llama gráfico de la función . Las representaciones gráficas de funciones también son posibles en otros sistemas de coordenadas. Por ejemplo, el gráfico de la función cuadrada $(x,y)\in G$

x\mapsto x^{2},

La representación en coordenadas cartesianas de la función cuadrática con el mismo gráfico formal, que consta de pares de números, da como resultado la conocida parábola . Si se representa en coordenadas polares la misma función cuadrática con el mismo gráfico formal, que consta de pares de números, el gráfico obtenido es la espiral de Fermat . $(x,x^{2})$ $x\in \mathbb {R} ,$ $x\mapsto x^{2},$ $(r,\theta )=(x,x^{2}),$

Tablas

Una función se puede representar como una tabla de valores. Si el dominio de una función es finito, entonces la función se puede especificar completamente de esta manera. Por ejemplo, la función de multiplicación definida como se puede representar mediante la conocida tabla de multiplicación $f:\{1,\ldots ,5\}^{2}\to \mathbb {R}$ $f(x,y)=xy$

Por otra parte, si el dominio de una función es continuo, una tabla puede dar los valores de la función en valores específicos del dominio. Si se necesita un valor intermedio, se puede utilizar la interpolación para estimar el valor de la función. Por ejemplo, una parte de una tabla para la función seno podría darse de la siguiente manera, con los valores redondeados a 6 decimales:

Antes de la llegada de las calculadoras portátiles y las computadoras personales, estas tablas solían compilarse y publicarse para funciones como logaritmos y funciones trigonométricas.

Gráfico de barras

Un diagrama de barras puede representar una función cuyo dominio es un conjunto finito, los números naturales o los enteros . En este caso, un elemento $x$ del dominio se representa mediante un intervalo del eje $x$ , y el valor correspondiente de la función, $f (x)$ , se representa mediante un rectángulo cuya base es el intervalo correspondiente a $x$ y cuya altura es $f (x)$ (posiblemente negativa, en cuyo caso la barra se extiende por debajo del eje $x$ ).

Propiedades generales

Esta sección describe las propiedades generales de las funciones, que son independientes de las propiedades específicas del dominio y del codominio.

Funciones estándar

Hay una serie de funciones estándar que ocurren con frecuencia:

Para cada conjunto $X$ , existe una función única, llamadafunción vacía , omapa vacío, delconjunto vacíoa $X$ . El gráfico de una función vacía es el conjunto vacío.^{[nota 5]}La existencia de funciones vacías es necesaria tanto para la coherencia de la teoría como para evitar excepciones relativas al conjunto vacío en muchas afirmaciones. Según la definición habitual de una función en la teoría de conjuntos como untriplete ordenado(o equivalentes), hay exactamente una función vacía para cada conjunto, por lo que la función vacíano es igual asi y solo si, aunque sus gráficos sean ambos elconjunto vacío. $\varnothing \to X$ $\varnothing \to Y$ $X\neq Y$
Para cada conjunto $X$ y cada conjunto singleton ${s}$ , existe una función única de $X$ a ${s}$ , que asigna cada elemento de $X$ a $s$ . Esto es una sobreyección (ver más abajo) a menos que $X$ sea el conjunto vacío.
Dada una función, la sobreyección canónica de $f$ sobre su imagen es la función de $X$ a $f$ $($ $X$ $)$ que asigna $x$ a $f$ $($ $x$ $)$ . $f:X\to Y,$ $f(X)=\{f(x)\mid x\in X\}$
Para cada subconjunto $A$ de un conjunto $X$ , la función de inclusión de $A$ en $X$ es la función inyectiva (ver más abajo) que asigna cada elemento de $A$ a sí mismo.
La función identidad en un conjunto $X$ , a menudo denotada por $id X$ , es la inclusión de $X$ en sí mismo.

Composición de funciones

Dadas dos funciones y tales que el dominio de $g$ es el codominio de $f$ , su composición es la función definida por $f:X\to Y$ $g:Y\to Z$ $g\circ f:X\rightarrow Z$

(g\circ f)(x)=g(f(x)).

Es decir, el valor de se obtiene aplicando primero $f$ a $x$ para obtener $y$ $=$ $f$ $($ $x$ $)$ y luego aplicando $g$ al resultado $y$ para obtener $g$ $($ $y$ $) =$ $g$ $($ $f$ $($ $x$ $))$ . En esta notación, la función que se aplica primero siempre se escribe a la derecha. $g\circ f$

La composición es una operación sobre funciones que se define solo si el codominio de la primera función es el dominio de la segunda. Incluso cuando ambas y satisfacen estas condiciones, la composición no es necesariamente conmutativa , es decir, las funciones y no necesitan ser iguales, sino que pueden entregar valores diferentes para el mismo argumento. Por ejemplo, sean $f$ $($ $x$ $) =$ $x$ $2$ y $g$ $($ $x$ $) =$ $x$ $+ 1$ , entonces y concuerdan solo para $g\circ f$ $g\circ f$ $f\circ g$ $g\circ f$ $f\circ g$ $g(f(x))=x^{2}+1$ $f(g(x))=(x+1)^{2}$ $x=0.$

La composición de funciones es asociativa en el sentido de que, si una de y está definida, entonces la otra también está definida, y son iguales, es decir, Por lo tanto, lo habitual es simplemente escribir $(h\circ g)\circ f$ $h\circ (g\circ f)$ $(h\circ g)\circ f=h\circ (g\circ f).$ $h\circ g\circ f.$

Las funciones identidad y son respectivamente una identidad derecha y una identidad izquierda para funciones de $X$ a $Y$ . Es decir, si $f$ es una función con dominio $X$ y codominio $Y$ , se tiene $\operatorname {id} _{X}$ $\operatorname {id} _{Y}$ $f\circ \operatorname {id} _{X}=\operatorname {id} _{Y}\circ f=f.$

Una función compuesta g ( f ( x )) puede visualizarse como la combinación de dos "máquinas".
Un ejemplo sencillo de composición de funciones
Otra composición. En este ejemplo, $(g \circ f)(c) = #$ .

Imagen y preimagen

Sea f la imagen bajo $f$ de un elemento $x$ $del$ dominio $X.$ ^[6] Si $A$ es cualquier subconjunto de $X$ , entonces la imagen de $A$ bajo $f$ , denotada $f$ $($ $A$ $)$ , es el subconjunto del codominio $Y que consiste$ $en$ todas las imágenes de elementos de $A$ , ^[6] $es$ decir $,$ $f:X\to Y.$

f(A)=\{f(x)\mid x\in A\}.

La imagen de $f$ es la imagen de todo el dominio, es decir, $f (X)$ . ^[17] También se le llama rango de $f$ , ^[6]^[7]^[8]^[9] aunque el término rango también puede referirse al codominio. ^[9]^[17]^[18]

Por otra parte, la imagen inversa o preimagen bajo $f$ de un elemento $y$ del codominio $Y$ es el conjunto de todos los elementos del dominio $X$ cuyas imágenes bajo $f$ son iguales $a y$ . ^[6] En símbolos, la preimagen de $y$ se denota por y se da por la ecuación $f^{-1}(y)$

f^{-1}(y)=\{x\in X\mid f(x)=y\}.

De la misma manera, la preimagen de un subconjunto $B$ del codominio $Y$ es el conjunto de las preimágenes de los elementos de $B$ , es decir, es el subconjunto del dominio $X$ constituido por todos los elementos de $X$ cuyas imágenes pertenecen a $B.$ ^[6] Se denota por y se da por la ecuación $f^{-1}(B)$

f^{-1}(B)=\{x\in X\mid f(x)\in B\}.

Por ejemplo, la preimagen de la función bajo el cuadrado es el conjunto . $\{4,9\}$ $\{-3,-2,2,3\}$

Por definición de función, la imagen de un elemento $x$ del dominio es siempre un único elemento del codominio. Sin embargo, la preimagen de un elemento $y$ del codominio puede estar vacía o contener cualquier número de elementos. Por ejemplo, si $f$ es la función de los números enteros a sí mismos que asigna cada número entero a 0, entonces . $f^{-1}(y)$ $f^{-1}(0)=\mathbb {Z}$

Si es una función, $A$ y $B$ son subconjuntos de $X$ , y $C$ y $D$ son subconjuntos de $Y$ , entonces se tienen las siguientes propiedades: $f:X\to Y$

$A\subseteq B\Longrightarrow f(A)\subseteq f(B)$
$C\subseteq D\Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)$
$A\subseteq f^{-1}(f(A))$
$C\supseteq f(f^{-1}(C))$
$f(f^{-1}(f(A)))=f(A)$
$f^{-1}(f(f^{-1}(C)))=f^{-1}(C)$

La preimagen por $f$ de un elemento $y$ del codominio se denomina a veces, en algunos contextos, la fibra de $y$ bajo $f$ .

Si una función $f$ tiene una inversa (ver abajo), esta inversa se denota En este caso puede denotar la imagen por o la preimagen por $f$ de $C$ . Esto no es un problema, ya que estos conjuntos son iguales. La notación y puede ser ambigua en el caso de conjuntos que contienen algunos subconjuntos como elementos, como En este caso, puede ser necesario tener cierto cuidado, por ejemplo, utilizando corchetes para imágenes y preimágenes de subconjuntos y paréntesis ordinarios para imágenes y preimágenes de elementos. $f^{-1}.$ $f^{-1}(C)$ $f^{-1}$ $f(A)$ $f^{-1}(C)$ $\{x,\{x\}\}.$ $f[A],f^{-1}[C]$

Funciones inyectivas, sobreyectivas y biyectivas

Sea una función. $f:X\to Y$

La función $f$ es inyectiva (o biunívoca , o es una inyección ) si $f (a) \neq f (b)$ para cada dos elementos diferentes $a$ y $b$ de $X$ . ^[17]^[19] De manera equivalente, $f$ es inyectiva si y solo si, para cada la preimagen contiene como máximo un elemento. Una función vacía siempre es inyectiva. Si $X$ no es el conjunto vacío, entonces $f$ es inyectiva si y solo si existe una función tal que es decir, si $f$ tiene una inversa izquierda . ^[19]Demostración : Si $f$ es inyectiva, para definir $g$ , se elige un elemento en $X$ (que existe ya que se supone que $X$ no está vacío), ^{[nota 6]} y se define $g$ por si y si A la inversa, si y entonces y por lo tanto $y\in Y,$ $f^{-1}(y)$ $g:Y\to X$ $g\circ f=\operatorname {id} _{X},$ $x_{0}$ $g(y)=x$ $y=f(x)$ $g(y)=x_{0}$ $y\not \in f(X).$ $g\circ f=\operatorname {id} _{X},$ $y=f(x),$ $x=g(y),$ $f^{-1}(y)=\{x\}.$

La función $f$ es sobreyectiva (o sobre , o es una sobreyección ) si su rango es igual a su codominio , es decir, si, para cada elemento del codominio, existe algún elemento del dominio tal que (en otras palabras, la preimagen de cada no es vacía). ^[17]^[20] Si, como es habitual en las matemáticas modernas, se supone el axioma de elección , entonces $f$ es sobreyectiva si y solo si existe una función tal que es decir, si $f$ tiene una inversa derecha . ^[20] El axioma de elección es necesario, porque, si $f$ es sobreyectiva, se define $g$ por donde es un elemento elegido arbitrariamente de $f(X)$ $Y$ $y$ $x$ $f(x)=y$ $f^{-1}(y)$ $y\in Y$ $g:Y\to X$ $f\circ g=\operatorname {id} _{Y},$ $g(y)=x,$ $x$ $f^{-1}(y).$

La función $f$ es biyectiva (o es una biyección o una correspondencia biyectiva ) si es a la vez inyectiva y sobreyectiva. ^[17]^[21] Es decir, $f$ es biyectiva si, para cada la preimagen contiene exactamente un elemento. La función $f$ es biyectiva si y sólo si admite una función inversa , es decir, una función tal que y ^[21] (Al contrario que en el caso de las sobreyecciones, esto no requiere el axioma de elección; la prueba es sencilla). $y\in Y,$ $f^{-1}(y)$ $g:Y\to X$ $g\circ f=\operatorname {id} _{X}$ $f\circ g=\operatorname {id} _{Y}.$

Toda función puede factorizarse como la composición de una sobreyección seguida de una inyección, donde $s$ es la sobreyección canónica de $X$ sobre $f$ $($ $X$ $)$ e $i$ es la inyección canónica de $f$ $($ $X$ $)$ en $Y$ . Esta es la factorización canónica de $f$ . $f:X\to Y$ $i\circ s$

"Uno a uno" y "sobre" son términos que eran más comunes en la literatura en lengua inglesa antigua; "inyectivo", "sobreyectivo" y "biyectivo" fueron acuñados originalmente como palabras francesas en el segundo cuarto del siglo XX por el grupo Bourbaki e importados al inglés. ^[22] Como advertencia, "una función uno a uno" es una que es inyectiva, mientras que una "correspondencia uno a uno" se refiere a una función biyectiva. Además, la afirmación " $f$ mapea $X$ sobre $Y$ " difiere de " $f$ mapea $X$ en $B$ ", en que la primera implica que $f$ es sobreyectiva, mientras que la segunda no hace ninguna afirmación sobre la naturaleza de $f$ . En un razonamiento complicado, la diferencia de una letra puede pasarse por alto fácilmente. Debido a la naturaleza confusa de esta terminología más antigua, estos términos han perdido popularidad en relación con los términos bourbakianos, que también tienen la ventaja de ser más simétricos.

Restricción y ampliación

Si es una función y $S$ es un subconjunto de $X$ , entonces la restricción de a S , denotada , es la función de $S$ a $Y$ definida por $f:X\to Y$ $f$ $f|_{S}$

f|_{S}(x)=f(x)

para todo $x$ en $S$ . Se pueden usar restricciones para definir funciones inversas parciales : si hay un subconjunto $S$ del dominio de una función tal que sea inyectiva, entonces la sobreyección canónica de sobre su imagen es una biyección, y por lo tanto tiene una función inversa de a $S$ . Una aplicación es la definición de funciones trigonométricas inversas . Por ejemplo, la función coseno es inyectiva cuando se restringe al intervalo $[0,$ $π$ $]$ . La imagen de esta restricción es el intervalo $[-1, 1]$ , y por lo tanto la restricción tiene una función inversa de $[-1, 1]$ a $[0,$ $π$ $]$ , que se llama arcocoseno y se denota $arccos$ . $f$ $f|_{S}$ $f|_{S}$ $f|_{S}(S)=f(S)$ $f(S)$

La restricción de funciones también se puede utilizar para "pegar" funciones. Sea la descomposición de $X$ como una unión de subconjuntos, y supongamos que se define una función en cada uno de ellos de modo que para cada par de índices, las restricciones de y a sean iguales. Entonces esto define una función única de modo que para todo $i$ . Esta es la forma en que se definen las funciones en variedades . ${\textstyle X=\bigcup _{i\in I}U_{i}}$ $f_{i}:U_{i}\to Y$ $U_{i}$ $i,j$ $f_{i}$ $f_{j}$ $U_{i}\cap U_{j}$ $f:X\to Y$ $f|_{U_{i}}=f_{i}$

Una extensión de una función $f$ es una función $g$ tal que $f$ es una restricción de $g$ . Un uso típico de este concepto es el proceso de continuación analítica , que permite extender funciones cuyo dominio es una pequeña parte del plano complejo a funciones cuyo dominio es casi todo el plano complejo.

He aquí otro ejemplo clásico de una extensión de función que se encuentra al estudiar homografías de la recta real . Una homografía es una función tal que $ad$ $-$ $bc$ $\neq 0$ . Su dominio es el conjunto de todos los números reales diferentes de y su imagen es el conjunto de todos los números reales diferentes de Si uno extiende la recta real a la recta real extendida proyectivamente incluyendo $\infty$ , uno puede extender $h$ a una biyección desde la recta real extendida a sí misma haciendo y . $h(x)={\frac {ax+b}{cx+d}}$ $-d/c,$ $a/c.$ $h(\infty )=a/c$ $h(-d/c)=\infty$

En cálculo

La idea de función, a partir del siglo XVII, fue fundamental para el nuevo cálculo infinitesimal . En ese momento, solo se consideraban funciones de valor real de una variable real y se suponía que todas las funciones eran suaves . Pero la definición pronto se extendió a funciones de varias variables y a funciones de una variable compleja . En la segunda mitad del siglo XIX, se introdujo la definición matemáticamente rigurosa de función y se definieron funciones con dominios y codominios arbitrarios.

En la actualidad, las funciones se utilizan en todas las áreas de las matemáticas. En el cálculo introductorio, cuando se utiliza la palabra función sin ninguna calificación, se refiere a una función de valor real de una única variable real. La definición más general de función suele presentarse a los estudiantes universitarios de segundo o tercer año de carreras STEM , y en el último año se les presenta el cálculo en un contexto más amplio y riguroso en cursos como análisis real y análisis complejo .

Función real

Gráfica de una función polinómica, aquí una función cuadrática.

Una función real es una función de valor real de una variable real , es decir, una función cuyo codominio es el cuerpo de números reales y cuyo dominio es un conjunto de números reales que contiene un intervalo . En esta sección, estas funciones se denominan simplemente funciones .

Las funciones que se consideran con más frecuencia en matemáticas y sus aplicaciones tienen cierta regularidad, es decir, son continuas , diferenciables e incluso analíticas . Esta regularidad garantiza que estas funciones puedan visualizarse mediante sus gráficos. En esta sección, todas las funciones son diferenciables en algún intervalo.

Las funciones disfrutan de operaciones puntuales , es decir, si $f$ y $g$ son funciones, su suma, diferencia y producto son funciones definidas por

{\begin{aligned}(f+g)(x)&=f(x)+g(x)\\(f-g)(x)&=f(x)-g(x)\\(f\cdot g)(x)&=f(x)\cdot g(x)\\\end{aligned}}.

Los dominios de las funciones resultantes son la intersección de los dominios de $f$ y $g$ . El cociente de dos funciones se define de manera similar mediante

{\frac {f}{g}}(x)={\frac {f(x)}{g(x)}},

pero el dominio de la función resultante se obtiene eliminando los ceros de $g$ de la intersección de los dominios de $f$ y $g$ .

Las funciones polinómicas se definen por polinomios y su dominio es el conjunto de números reales. Entre ellas se encuentran las funciones constantes , las funciones lineales y las funciones cuadráticas . Las funciones racionales son cocientes de dos funciones polinómicas y su dominio son los números reales con un número finito de ellos eliminados para evitar la división por cero . La función racional más simple es la función cuyo gráfico es una hipérbola y cuyo dominio es toda la recta real excepto el 0. $x\mapsto {\frac {1}{x}},$

La derivada de una función real diferenciable es una función real. Una antiderivada de una función real continua es una función real que tiene como derivada la función original. Por ejemplo, la función es continua, e incluso diferenciable, en los números reales positivos. Por lo tanto, una antiderivada que toma el valor cero para $x$ $= 1$ es una función diferenciable llamada logaritmo natural . ${\textstyle x\mapsto {\frac {1}{x}}}$

Una función real $f$ es monótona en un intervalo si el signo de no depende de la elección de $x$ e $y$ en el intervalo. Si la función es diferenciable en el intervalo, es monótona si el signo de la derivada es constante en el intervalo. Si una función real $f$ es monótona en un intervalo $I$ , tiene una función inversa , que es una función real con dominio $f$ $($ $I$ $)$ e imagen $I$ . Así es como se definen las funciones trigonométricas inversas en términos de funciones trigonométricas , donde las funciones trigonométricas son monótonas. Otro ejemplo: el logaritmo natural es monótono sobre los números reales positivos, y su imagen es toda la recta real; por lo tanto, tiene una función inversa que es una biyección entre los números reales y los números reales positivos. Esta inversa es la función exponencial . ${\frac {f(x)-f(y)}{x-y}}$

Muchas otras funciones reales se definen ya sea por el teorema de la función implícita (la función inversa es un caso particular) o como soluciones de ecuaciones diferenciales . Por ejemplo, las funciones seno y coseno son las soluciones de la ecuación diferencial lineal .

y''+y=0

de tal manera que

\sin 0=0,\quad \cos 0=1,\quad {\frac {\partial \sin x}{\partial x}}(0)=1,\quad {\frac {\partial \cos x}{\partial x}}(0)=0.

Función con valores vectoriales

Cuando los elementos del codominio de una función son vectores , se dice que la función es una función de valor vectorial. Estas funciones son particularmente útiles en aplicaciones, por ejemplo, en el modelado de propiedades físicas. Por ejemplo, la función que asocia a cada punto de un fluido su vector de velocidad es una función de valor vectorial.

Algunas funciones con valores vectoriales se definen en un subconjunto de u otros espacios que comparten propiedades geométricas o topológicas de , como las variedades . Estas funciones con valores vectoriales reciben el nombre de campos vectoriales . $\mathbb {R} ^{n}$ $\mathbb {R} ^{n}$

Espacio funcional

En análisis matemático , y más específicamente en análisis funcional , un espacio de funciones es un conjunto de funciones escalares o vectoriales , que comparten una propiedad específica y forman un espacio vectorial topológico . Por ejemplo, las funciones reales suaves con un soporte compacto (es decir, que son cero fuera de algún conjunto compacto ) forman un espacio de funciones que está en la base de la teoría de distribuciones .

Los espacios funcionales juegan un papel fundamental en el análisis matemático avanzado, al permitir el uso de sus propiedades algebraicas y topológicas para el estudio de las propiedades de las funciones. Por ejemplo, todos los teoremas de existencia y unicidad de soluciones de ecuaciones diferenciales ordinarias o parciales son resultado del estudio de los espacios funcionales.

Funciones multivaluadas

Varios métodos para especificar funciones de variables reales o complejas parten de una definición local de la función en un punto o en un entorno de un punto y luego extienden por continuidad la función a un dominio mucho más grande. Con frecuencia, para un punto de partida hay varios valores iniciales posibles para la función. $x_{0},$

Por ejemplo, al definir la raíz cuadrada como la función inversa de la función cuadrada, para cualquier número real positivo hay dos opciones para el valor de la raíz cuadrada, una de las cuales es positiva y se denota y otra que es negativa y se denota Estas opciones definen dos funciones continuas, ambas teniendo los números reales no negativos como dominio, y teniendo los números reales no negativos o no positivos como imágenes. Al observar los gráficos de estas funciones, se puede ver que, juntas, forman una única curva suave . Por lo tanto, a menudo es útil considerar estas dos funciones de raíz cuadrada como una única función que tiene dos valores para $x$ positivo , un valor para 0 y ningún valor para $x$ negativo . $x_{0},$ ${\sqrt {x_{0}}},$ $-{\sqrt {x_{0}}}.$

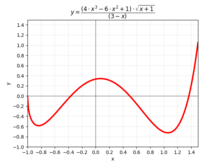
En el ejemplo anterior, una opción, la raíz cuadrada positiva, es más natural que la otra. Este no es el caso en general. Por ejemplo, consideremos la función implícita que asigna $y$ a una raíz $x$ de (ver la figura de la derecha). Para $y$ $= 0$ se puede elegir cualquiera de las dos para $x$ . Por el teorema de la función implícita , cada opción define una función; para la primera, el dominio (máximo) es el intervalo $[-2, 2]$ y la imagen es $[-1, 1]$ ; para la segunda, el dominio es $[-2, \infty)$ y la imagen es $[1, \infty)$ ; para el último, el dominio es $(-\infty, 2]$ y la imagen es $(-\infty, -1]$ . Como los tres gráficos juntos forman una curva suave, y no hay razón para preferir una opción, estas tres funciones a menudo se consideran como una única función multivaluada de $y$ que tiene tres valores para $-2 <$ $y$ $< 2$ , y solo un valor para $y$ $\leq -2$ e $y$ $\geq -2$ . $x^{3}-3x-y=0$ $0,{\sqrt {3}},{\text{ or }}-{\sqrt {3}}$

La utilidad del concepto de funciones multivaluadas es más clara cuando se consideran funciones complejas, típicamente funciones analíticas . El dominio al que se puede extender una función compleja por continuación analítica generalmente consiste en casi todo el plano complejo . Sin embargo, cuando se extiende el dominio a través de dos caminos diferentes, a menudo se obtienen valores diferentes. Por ejemplo, cuando se extiende el dominio de la función raíz cuadrada, a lo largo de un camino de números complejos con partes imaginarias positivas, se obtiene $i$ para la raíz cuadrada de −1; mientras que, cuando se extiende a través de números complejos con partes imaginarias negativas, se obtiene $- i$ . Generalmente hay dos formas de resolver el problema. Se puede definir una función que no es continua a lo largo de alguna curva, llamada corte de rama . Tal función se llama el valor principal de la función. La otra forma es considerar que se tiene una función multivaluada , que es analítica en todas partes excepto para singularidades aisladas, pero cuyo valor puede "saltar" si se sigue un bucle cerrado alrededor de una singularidad. Este salto se llama monodromía .

En los fundamentos de las matemáticas

La definición de función que se da en este artículo requiere el concepto de conjunto , ya que el dominio y el codominio de una función deben ser un conjunto. Esto no es un problema en las matemáticas habituales, ya que generalmente no es difícil considerar solo funciones cuyo dominio y codominio son conjuntos, que están bien definidos, incluso si el dominio no está definido explícitamente. Sin embargo, a veces es útil considerar funciones más generales.

Por ejemplo, el conjunto singleton puede considerarse como una función cuyo dominio incluiría todos los conjuntos y, por lo tanto, no sería un conjunto. En las matemáticas habituales, se evita este tipo de problemas especificando un dominio, lo que significa que se tienen muchas funciones singleton. Sin embargo, al establecer los fundamentos de las matemáticas, es posible que haya que utilizar funciones cuyo dominio, codominio o ambos no estén especificados, y algunos autores, a menudo lógicos, dan una definición precisa de estas funciones débilmente especificadas. ^[23] $x\mapsto \{x\}.$

Estas funciones generalizadas pueden ser fundamentales en el desarrollo de una formalización de los fundamentos de las matemáticas . Por ejemplo, la teoría de conjuntos de Von Neumann–Bernays–Gödel es una extensión de la teoría de conjuntos en la que la colección de todos los conjuntos es una clase . Esta teoría incluye el axioma de reemplazo , que puede enunciarse como: Si $X$ es un conjunto y $F$ es una función, entonces $F [X]$ es un conjunto.

En formulaciones alternativas de los fundamentos de las matemáticas que utilizan la teoría de tipos en lugar de la teoría de conjuntos, las funciones se toman como nociones primitivas en lugar de definirse a partir de otros tipos de objetos. Son habitantes de los tipos de función y pueden construirse utilizando expresiones del cálculo lambda . ^[24]

En informática

En programación informática , una función es, en general, una pieza de un programa informático , que implementa el concepto abstracto de función. Es decir, es una unidad de programa que produce una salida por cada entrada. Sin embargo, en muchos lenguajes de programación se denomina función a toda subrutina , incluso cuando no existe salida, y cuando la funcionalidad consiste simplemente en modificar algún dato en la memoria del ordenador .

La programación funcional es el paradigma de programación que consiste en construir programas utilizando únicamente subrutinas que se comportan como funciones matemáticas. Por ejemplo, if_then_elsees una función que toma tres funciones como argumentos y, dependiendo del resultado de la primera función ( verdadero o falso ), devuelve el resultado de la segunda o la tercera función. Una ventaja importante de la programación funcional es que facilita la demostración de los programas , ya que se basa en una teoría bien fundamentada, el cálculo lambda (ver más abajo).

Excepto en la terminología del lenguaje informático, "función" tiene el significado matemático habitual en informática . En esta área, una propiedad de gran interés es la computabilidad de una función. Para dar un significado preciso a este concepto, y al concepto relacionado de algoritmo , se han introducido varios modelos de computación , siendo los más antiguos las funciones recursivas generales , el cálculo lambda y la máquina de Turing . El teorema fundamental de la teoría de la computabilidad es que estos tres modelos de computación definen el mismo conjunto de funciones computables, y que todos los demás modelos de computación que se han propuesto definen el mismo conjunto de funciones computables o uno más pequeño. La tesis de Church-Turing es la afirmación de que toda definición filosóficamente aceptable de una función computable define también las mismas funciones.

Las funciones recursivas generales son funciones parciales de números enteros a números enteros que se pueden definir a partir de

a través de los operadores

Aunque se definen sólo para funciones de números enteros a enteros, pueden modelar cualquier función computable como consecuencia de las siguientes propiedades:

Un cálculo es la manipulación de secuencias finitas de símbolos (dígitos de números, fórmulas, ...),
Cada secuencia de símbolos puede codificarse como una secuencia de bits ,
Una secuencia de bits se puede interpretar como la representación binaria de un entero.

El cálculo lambda es una teoría que define funciones computables sin utilizar la teoría de conjuntos y es la base teórica de la programación funcional. Consiste en términos que son variables, definiciones de funciones ( términos 𝜆 ) o aplicaciones de funciones a términos. Los términos se manipulan mediante algunas reglas (la $α$ -equivalencia, la $β$ -reducción y la $η$ -conversión), que son los axiomas de la teoría y pueden interpretarse como reglas de cálculo.

En su forma original, el cálculo lambda no incluye los conceptos de dominio y codominio de una función. En términos generales, se han introducido en la teoría con el nombre de tipo en el cálculo lambda tipificado . La mayoría de los tipos de cálculos lambda tipificados pueden definir menos funciones que el cálculo lambda no tipificado.

Véase también

Subpáginas

Generalizaciones

Temas relacionados

Notas

^ Esta definición de "grafo" se refiere a un conjunto de pares de objetos. Los gráficos, en el sentido de diagramas , son más aplicables a funciones que van desde los números reales hasta ellos mismos. Todas las funciones pueden describirse mediante conjuntos de pares, pero puede que no sea práctico construir un diagrama para funciones entre otros conjuntos (como conjuntos de matrices).
^ El verdadero dominio de dicha función a menudo se denomina dominio de definición de la función.
^ $n$ también puede ser 1, lo que incluye funciones definidas anteriormente. Para $n = 0$ , cada constante también es un caso especial de una función multivariable.
^ Aquí "elemental" no tiene exactamente su sentido común: aunque la mayoría de las funciones que se encuentran en los cursos elementales de matemáticas son elementales en este sentido, algunas funciones elementales no son elementales para el sentido común, por ejemplo, aquellas que involucran raíces de polinomios de alto grado.
^ Por definición, la gráfica de la función vacía de $X$ es un subconjunto del producto cartesiano $\emptyset \times X$ , y este producto está vacío.
^ El axioma de elección no es necesario aquí, ya que la elección se realiza en un único conjunto.

Referencias

^ Halmos 1970, p. 30; las palabras mapa , mapeo , transformación , correspondencia y operador a veces se usan como sinónimos.
^ Halmos 1970
^ "Mapeo". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].
^ "función | Definición, tipos, ejemplos y hechos". Enciclopedia Británica . Consultado el 17 de agosto de 2020 .
^ Spivak 2008, pág. 39.
^ abcdef Kudryavtsev, LD (2001) [1994]. "Función". Enciclopedia de Matemáticas . EMS Press .
^ ab Taalman, Laura ; Kohn, Peter (2014). Cálculo . Nueva York : WH Freeman and Company . p. 3. ISBN 978-1-4292-4186-1. OCLC 856545590. OL 27544563M .
^ ab Trench, William F. (2013) [2003]. Introducción al análisis real (2.04.ª ed.). Pearson Education (originalmente; reeditado por el autor). pp. 30–32. ISBN 0-13-045786-8. LCCN 2002032369. OCLC 953799815. Zbl 1204.00023.
^ abc Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Análisis real elemental (PDF) (2.ª ed.). Prentice Hall (originalmente; 2.ª ed. republicada por los autores). pp. A-4–A-5. ISBN 978-1-4348-4367-8. OCLC 1105855173. OL 31844948M. Zbl 0872.26001.
^ Halmos, Paul R. (1974). Teoría de conjuntos ingenua . Springer. págs. 30–33.
^ Larson, Ron; Edwards, Bruce H. (2010). Cálculo de una sola variable . Cengage Learning. pág. 19. ISBN 978-0-538-73552-0.
^ Weisstein, Eric W. "Mapa". mathworld.wolfram.com . Consultado el 12 de junio de 2019 .
^ ab Lang, Serge (1987). "III §1. Aplicaciones". Álgebra lineal (3.ª ed.). Springer. pág. 43. ISBN 978-0-387-96412-6Una función es un tipo especial de aplicación, es decir , es una aplicación de un conjunto al conjunto de números, es decir, a R o C o a un campo K.
^ ab Apostol, TM (1981). Análisis matemático (2.ª ed.). Addison-Wesley. pág. 35. ISBN 978-0-201-00288-1.OCLC 928947543 .
^ James, Robert C. ; James, Glenn (1992). Diccionario de matemáticas (quinta edición). Van Nostrand Reinhold. pág. 202. ISBN 0-442-00741-8.OCLC 25409557 .
^ James y James 1992, pág. 48
^ abcde Gowers, Timothy ; Barrow-Green, June ; Leader, Imre , eds. (2008). The Princeton Companion to Mathematics . Princeton, Nueva Jersey : Princeton University Press . p. 11. doi :10.1515/9781400830398. ISBN 978-0-691-11880-2. JSTOR j.ctt7sd01. LCCN 2008020450. SEÑOR 2467561. OCLC 227205932. OL 19327100M. Zbl 1242.00016.
^ Cantidades y unidades - Parte 2: Signos y símbolos matemáticos para su uso en las ciencias naturales y la tecnología , pág. 15. ISO 80000-2 (ISO/IEC 2009-12-01)
^ ab Ivanova, OA (2001) [1994]. "Inyección". Enciclopedia de Matemáticas . EMS Press .
^ ab Ivanova, OA (2001) [1994]. "Surjection". Enciclopedia de Matemáticas . EMS Press .
^ ab Ivanova, OA (2001) [1994]. "Biyección". Enciclopedia de Matemáticas . EMS Press .
^ Hartnett, Kevin (9 de noviembre de 2020). "Dentro de la sociedad secreta de matemáticas conocida simplemente como Nicolas Bourbaki". Quanta Magazine . Consultado el 5 de junio de 2024 .
^ Gödel 1940, pag. 16; Jech 2003, pág. 11; Cunningham 2016, pág. 57
^ Klev, Ansten (2019). "Una comparación de la teoría de tipos con la teoría de conjuntos". En Centrone, Stefania; Kant, Deborah; Sarikaya, Deniz (eds.). Reflexiones sobre los fundamentos de las matemáticas: fundamentos univalentes, teoría de conjuntos y pensamientos generales . Biblioteca Synthese. Vol. 407. Cham: Springer. págs. 271–292. doi :10.1007/978-3-030-15655-8_12. ISBN . 978-3-030-15654-1.Señor 4352345 .

Fuentes

Bartle, Robert (1976). Los elementos del análisis real (2.ª ed.). Wiley. ISBN 978-0-471-05465-8.OCLC 465115030 .
Bloch, Ethan D. (2011). Demostraciones y fundamentos: un primer curso de matemáticas abstractas. Springer. ISBN 978-1-4419-7126-5.
Cunningham, Daniel W. (2016). Teoría de conjuntos: un primer curso . Cambridge University Press. ISBN 978-1-107-12032-7.
Gödel, Kurt (1940). La consistencia de la hipótesis del continuo . Princeton University Press. ISBN 978-0-691-07927-1.
Halmos, Paul R. (1970). Teoría de conjuntos ingenua. Springer-Verlag. ISBN 978-0-387-90092-6.
Jech, Thomas (2003). Teoría de conjuntos (3ª ed.). Springer-Verlag . ISBN 978-3-540-44085-7.
Spivak, Michael (2008). Cálculo (4.ª ed.). Publicar o perecer. ISBN 978-0-914098-91-1.

Lectura adicional

Anton, Howard (1980). Cálculo con geometría analítica . Wiley . ISBN. 978-0-471-03248-9.
Bartle, Robert G. (1976). Los elementos del análisis real (2.ª ed.). Wiley. ISBN 978-0-471-05464-1.
Dubinsky, Ed; Harel, Guershon (1992). El Concepto de Función: Aspectos de Epistemología y Pedagogía . Asociación Matemática de América. ISBN 978-0-88385-081-7.
Hammack, Richard (2009). "12. Funciones" (PDF) . Libro de pruebas. Virginia Commonwealth University . Consultado el 1 de agosto de 2012 .
Husch, Lawrence S. (2001). Visual Calculus. Universidad de Tennessee . Consultado el 27 de septiembre de 2007 .
Katz, Robert (1964). Análisis axiomático . DC Heath and Company .
Kleiner, Israel (1989). "Evolución del concepto de función: un breve estudio". The College Mathematics Journal . 20 (4): 282–300. CiteSeerX 10.1.1.113.6352 . doi :10.2307/2686848. JSTOR 2686848.
Lützen, Jesper (2003). "Entre el rigor y las aplicaciones: desarrollos en el concepto de función en el análisis matemático". En Porter, Roy (ed.). La historia de la ciencia de Cambridge: las ciencias físicas y matemáticas modernas . Cambridge University Press. ISBN 978-0-521-57199-9.Una presentación histórica accesible y entretenida.
Malik, MA (1980). "Aspectos históricos y pedagógicos de la definición de función". Revista Internacional de Educación Matemática en Ciencia y Tecnología . 11 (4): 489–492. doi :10.1080/0020739800110404.
Reichenbach, Hans (1947). Elementos de lógica simbólica . Dover. ISBN 0-486-24004-5.
Ruthing, D. (1984). "Old Intelligencer: Algunas definiciones del concepto de función desde Bernoulli, Joh. hasta Bourbaki, N." Mathematical Intelligencer . 6 (4): 71–78. doi :10.1007/BF03026743. S2CID 189883712.
Thomas, George B.; Finney, Ross L. (1995). Cálculo y geometría analítica (novena edición). Addison-Wesley . ISBN 978-0-201-53174-9.

Enlaces externos

Wikimedia Commons tiene medios relacionados con Funciones (matemáticas) .

The Wolfram Functions: sitio web que ofrece fórmulas y visualizaciones de muchas funciones matemáticas
Biblioteca digital de funciones matemáticas del NIST