La física matemática se refiere al desarrollo de métodos matemáticos para su aplicación a problemas de física . El Journal of Mathematical Physics define el campo como "la aplicación de las matemáticas a problemas de física y el desarrollo de métodos matemáticos adecuados para tales aplicaciones y para la formulación de teorías físicas". [1] Una definición alternativa incluiría también aquellas matemáticas que se inspiran en la física, conocidas como matemáticas físicas . [2]
Hay varias ramas distintas de la física matemática, y éstas corresponden aproximadamente a partes históricas particulares de nuestro mundo.
La aplicación de las técnicas de la física matemática a la mecánica clásica implica típicamente la reformulación rigurosa, abstracta y avanzada de la mecánica newtoniana en términos de la mecánica lagrangiana y la mecánica hamiltoniana (incluidos ambos enfoques en presencia de restricciones). Ambas formulaciones están incorporadas en la mecánica analítica y conducen a una comprensión de la profunda interacción entre las nociones de simetría y cantidades conservadas durante la evolución dinámica de los sistemas mecánicos, tal como se expresa en la formulación más elemental del teorema de Noether . Estos enfoques e ideas se han extendido a otras áreas de la física, como la mecánica estadística , la mecánica del continuo , la teoría clásica de campos y la teoría cuántica de campos . Además, han proporcionado múltiples ejemplos e ideas en geometría diferencial (por ejemplo, varias nociones en geometría simpléctica y conjuntos de vectores ).
Dentro de las matemáticas propiamente dichas, la teoría de la ecuación diferencial parcial , el cálculo variacional , el análisis de Fourier , la teoría del potencial y el análisis vectorial están quizás más estrechamente asociadas con la física matemática. Estos campos se desarrollaron intensamente desde la segunda mitad del siglo XVIII (por ejemplo, por D'Alembert , Euler y Lagrange ) hasta la década de 1930. Las aplicaciones físicas de estos desarrollos incluyen hidrodinámica , mecánica celeste , mecánica continua , teoría de la elasticidad , acústica , termodinámica , electricidad , magnetismo y aerodinámica .
La teoría de los espectros atómicos (y, más tarde, la mecánica cuántica ) se desarrolló casi al mismo tiempo que algunas partes de los campos matemáticos del álgebra lineal , la teoría espectral de operadores , las álgebras de operadores y, más ampliamente, el análisis funcional . La mecánica cuántica no relativista incluye operadores de Schrödinger y tiene conexiones con la física atómica y molecular . La teoría de la información cuántica es otra subespecialidad.
Las teorías especial y general de la relatividad requieren un tipo de matemática bastante diferente. Se trataba de la teoría de grupos , que desempeñó un papel importante tanto en la teoría cuántica de campos como en la geometría diferencial . Sin embargo, esto se fue complementando gradualmente con la topología y el análisis funcional en la descripción matemática de los fenómenos cosmológicos y de la teoría cuántica de campos . En la descripción matemática de estas áreas físicas, también son importantes algunos conceptos del álgebra homológica y de la teoría de categorías [3] .
La mecánica estadística forma un campo separado, que incluye la teoría de las transiciones de fase . Se basa en la mecánica hamiltoniana (o su versión cuántica) y está estrechamente relacionada con la teoría ergódica más matemática y algunas partes de la teoría de la probabilidad . Cada vez existen más interacciones entre la combinatoria y la física , en particular la física estadística.
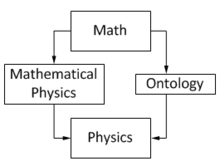
El uso del término "física matemática" es a veces idiosincrásico . Ciertas partes de las matemáticas que surgieron inicialmente del desarrollo de la física no se consideran, de hecho, partes de la física matemática, mientras que otros campos estrechamente relacionados sí lo son. Por ejemplo, las ecuaciones diferenciales ordinarias y la geometría simpléctica generalmente se consideran disciplinas puramente matemáticas, mientras que los sistemas dinámicos y la mecánica hamiltoniana pertenecen a la física matemática. John Herapath utilizó el término para el título de su texto de 1847 sobre "principios matemáticos de la filosofía natural", siendo el alcance en ese momento "las causas del calor, la elasticidad de los gases, la gravitación y otros grandes fenómenos de la naturaleza". [4]
El término "física matemática" se utiliza a veces para denotar investigaciones destinadas a estudiar y resolver problemas de física o experimentos mentales dentro de un marco matemáticamente riguroso . En este sentido, la física matemática cubre un ámbito académico muy amplio que se distingue sólo por la combinación de algún aspecto matemático y un aspecto de la física teórica. Aunque está relacionada con la física teórica , [5] la física matemática en este sentido enfatiza el rigor matemático de tipo similar al que se encuentra en las matemáticas.
Por otro lado, la física teórica enfatiza los vínculos con las observaciones y la física experimental , lo que a menudo requiere que los físicos teóricos (y los físicos matemáticos en el sentido más general) utilicen argumentos heurísticos , intuitivos o aproximados. [6] Estos argumentos no son considerados rigurosos por los matemáticos.
Estos físicos matemáticos amplían y aclaran principalmente las teorías físicas . Debido al nivel requerido de rigor matemático, estos investigadores a menudo se ocupan de cuestiones que los físicos teóricos consideraban ya resueltas. Sin embargo, a veces pueden mostrar que la solución anterior era incompleta, incorrecta o simplemente demasiado ingenua. Ejemplos de ello son los intentos de inferir la segunda ley de la termodinámica a partir de la mecánica estadística . [ cita necesaria ] Otros ejemplos se refieren a las sutilezas involucradas con los procedimientos de sincronización en la relatividad especial y general ( efecto Sagnac y sincronización de Einstein ).
El esfuerzo por poner las teorías físicas sobre una base matemáticamente rigurosa no sólo desarrolló la física sino que también ha influido en el desarrollo de algunas áreas matemáticas. Por ejemplo, el desarrollo de la mecánica cuántica y algunos aspectos del análisis funcional son paralelos en muchos aspectos. El estudio matemático de la mecánica cuántica , la teoría cuántica de campos y la mecánica estadística cuántica ha motivado resultados en álgebras de operadores . El intento de construir una formulación matemática rigurosa de la teoría cuántica de campos también ha producido algunos avances en campos como la teoría de la representación .
Existe una tradición de análisis matemático de la naturaleza que se remonta a los antiguos griegos; los ejemplos incluyen a Euclides ( Óptica ), Arquímedes ( Sobre el equilibrio de los planos , Sobre cuerpos flotantes ) y Ptolomeo ( Óptica , Armónicos ). [7] [8] Más tarde, los eruditos islámicos y bizantinos se basaron en estas obras, que finalmente fueron reintroducidas o estuvieron disponibles para Occidente en el siglo XII y durante el Renacimiento .
En la primera década del siglo XVI, el astrónomo aficionado Nicolás Copérnico propuso el heliocentrismo y publicó un tratado sobre él en 1543. Conservó la idea ptolemaica de los epiciclos y simplemente buscó simplificar la astronomía construyendo conjuntos más simples de órbitas epicíclicas. Los epiciclos consisten en círculos sobre círculos. Según la física aristotélica , el círculo era la forma perfecta de movimiento, y era el movimiento intrínseco del quinto elemento de Aristóteles —la quintaesencia o esencia universal conocida en griego como éter para los ingleses aire puro— , que era la sustancia pura más allá de la esfera sublunar . y así era la composición pura de las entidades celestiales. El alemán Johannes Kepler [1571-1630], asistente de Tycho Brahe , modificó las órbitas copernicanas a elipses , formalizadas en las ecuaciones de las leyes del movimiento planetario de Kepler .
Galileo Galilei , un atomista entusiasta, en su libro de 1623 The Assayer afirmó que "el libro de la naturaleza está escrito en matemáticas". [9] Su libro de 1632, sobre sus observaciones telescópicas, apoyaba el heliocentrismo. [10] Después de haber introducido la experimentación, Galileo refutó la cosmología geocéntrica refutando la propia física aristotélica. El libro de Galileo de 1638, Discurso sobre dos nuevas ciencias, estableció la ley de caída libre igual, así como los principios del movimiento inercial, fundando los conceptos centrales de lo que se convertiría en la mecánica clásica actual . [10] Por la ley de inercia de Galileo, así como por el principio de invariancia de Galileo , también llamado relatividad de Galileo, para cualquier objeto que experimente inercia, existe una justificación empírica para saber sólo que está en reposo o movimiento relativo : reposo o movimiento con respecto a otro objeto.
René Descartes desarrolló un sistema completo de cosmología heliocéntrica basado en el principio del movimiento de vórtice, la física cartesiana , cuya amplia aceptación provocó la desaparición de la física aristotélica. Descartes buscó formalizar el razonamiento matemático en la ciencia y desarrolló coordenadas cartesianas para trazar geométricamente ubicaciones en el espacio 3D y marcar sus progresiones a lo largo del flujo del tiempo. [11]
Un contemporáneo mayor de Newton, Christiaan Huygens , fue el primero en idealizar un problema físico mediante un conjunto de parámetros y el primero en matematizar completamente una explicación mecanicista de fenómenos físicos no observables, y por estas razones Huygens es considerado el primer físico teórico y uno de los los fundadores de la física matemática moderna. [12] [13]
En esta era, conceptos importantes en cálculo como el teorema fundamental del cálculo (probado en 1668 por el matemático escocés James Gregory [14] ) y la búsqueda de extremos y mínimos de funciones mediante la diferenciación utilizando el teorema de Fermat (por el matemático francés Pierre de Fermat ) ya eran conocido antes de Leibniz y Newton. Isaac Newton (1642-1727) desarrolló algunos conceptos de cálculo (aunque Gottfried Wilhelm Leibniz desarrolló conceptos similares fuera del contexto de la física) y el método de Newton para resolver problemas de física. Tuvo mucho éxito en su aplicación del cálculo a la teoría del movimiento. La teoría del movimiento de Newton, expuesta en sus Principios matemáticos de la filosofía natural, publicados en 1687, [15] modeló tres leyes galileanas del movimiento junto con la ley de gravitación universal de Newton en un marco de espacio absoluto , planteado por Newton como una entidad físicamente real de Estructura geométrica euclidiana que se extiende infinitamente en todas direcciones, al tiempo que supone el tiempo absoluto , lo que supuestamente justifica el conocimiento del movimiento absoluto, el movimiento del objeto con respecto al espacio absoluto. El principio de invariancia/relatividad galileana estaba simplemente implícito en la teoría del movimiento de Newton. Habiendo reducido ostensiblemente las leyes celestes del movimiento de Kepler, así como las leyes del movimiento terrestre de Galileo, a una fuerza unificadora, Newton logró un gran rigor matemático, pero con laxitud teórica. [dieciséis]
En el siglo XVIII, el suizo Daniel Bernoulli (1700-1782) hizo contribuciones a la dinámica de fluidos y a las cuerdas vibrantes . El suizo Leonhard Euler (1707-1783) realizó un trabajo especial en cálculo variacional , dinámica, dinámica de fluidos y otras áreas. También se destacó el francés nacido en Italia Joseph-Louis Lagrange (1736-1813) por su trabajo en mecánica analítica : formuló la mecánica lagrangiana y los métodos variacionales. El físico, astrónomo y matemático irlandés William Rowan Hamilton (1805-1865) también hizo una contribución importante a la formulación de la dinámica analítica, llamada dinámica hamiltoniana. La dinámica hamiltoniana había desempeñado un papel importante en la formulación de las teorías modernas de la física, incluidas la teoría de campos y la mecánica cuántica. El físico matemático francés Joseph Fourier (1768 – 1830) introdujo la noción de serie de Fourier para resolver la ecuación de calor , dando lugar a un nuevo enfoque para la resolución de ecuaciones diferenciales parciales mediante transformadas integrales .
A principios del siglo XIX, los siguientes matemáticos de Francia, Alemania e Inglaterra habían contribuido a la física matemática. El francés Pierre-Simon Laplace (1749-1827) hizo importantes contribuciones a la astronomía matemática y la teoría del potencial . Siméon Denis Poisson (1781-1840) trabajó en mecánica analítica y teoría de potenciales . En Alemania, Carl Friedrich Gauss (1777–1855) hizo contribuciones clave a los fundamentos teóricos de la electricidad , el magnetismo , la mecánica y la dinámica de fluidos . En Inglaterra, George Green (1793-1841) publicó Un ensayo sobre la aplicación del análisis matemático a las teorías de la electricidad y el magnetismo en 1828, que además de sus importantes contribuciones a las matemáticas hizo avances tempranos hacia el establecimiento de los fundamentos matemáticos de la electricidad y el magnetismo. magnetismo.
Un par de décadas antes de la publicación de Newton de una teoría de partículas de la luz, el holandés Christiaan Huygens (1629-1695) desarrolló la teoría ondulatoria de la luz, publicada en 1690. En 1804, el experimento de la doble rendija de Thomas Young reveló un patrón de interferencia. , como si la luz fuera una onda, y así se aceptó la teoría ondulatoria de la luz de Huygens, así como la inferencia de Huygens de que las ondas de luz eran vibraciones del éter luminífero . Jean-Augustin Fresnel modeló el comportamiento hipotético del éter. El físico inglés Michael Faraday introdujo el concepto teórico de campo, no de acción a distancia. A mediados del siglo XIX, el escocés James Clerk Maxwell (1831-1879) redujo la electricidad y el magnetismo a la teoría del campo electromagnético de Maxwell, reducida por otros a las cuatro ecuaciones de Maxwell . Inicialmente, se consideró que la óptica era consecuencia del campo de [ se necesita aclaración ] de Maxwell. Más tarde se descubrió que la radiación y el espectro electromagnético actual también eran consecuencia de este campo electromagnético .
El físico inglés Lord Rayleigh [1842-1919] trabajó en el sonido . Los irlandeses William Rowan Hamilton (1805–1865), George Gabriel Stokes (1819–1903) y Lord Kelvin (1824–1907) produjeron varias obras importantes: Stokes fue un líder en óptica y dinámica de fluidos; Kelvin hizo importantes descubrimientos en termodinámica ; Hamilton realizó un trabajo notable en mecánica analítica , descubriendo un enfoque nuevo y poderoso hoy conocido como mecánica hamiltoniana . Contribuciones muy relevantes a este enfoque se deben a su colega alemán, el matemático Carl Gustav Jacobi (1804-1851), en particular en referencia a las transformaciones canónicas . El alemán Hermann von Helmholtz (1821-1894) hizo importantes contribuciones en los campos del electromagnetismo , las ondas, los fluidos y el sonido. En Estados Unidos, el trabajo pionero de Josiah Willard Gibbs (1839-1903) se convirtió en la base de la mecánica estadística . El alemán Ludwig Boltzmann (1844-1906) logró resultados teóricos fundamentales en este campo . Juntos, estos individuos sentaron las bases de la teoría electromagnética, la dinámica de fluidos y la mecánica estadística.
En la década de 1880, existía una importante paradoja: un observador dentro del campo electromagnético de Maxwell lo medía a una velocidad aproximadamente constante, independientemente de la velocidad del observador en relación con otros objetos dentro del campo electromagnético. Así, aunque la velocidad del observador se perdía continuamente [ se necesita aclaración ] en relación con el campo electromagnético, se conservaba en relación con otros objetos en el campo electromagnético. Y, sin embargo, no se detectó ninguna violación de la invariancia galileana en las interacciones físicas entre objetos. Como el campo electromagnético de Maxwell se modeló como oscilaciones del éter , los físicos dedujeron que el movimiento dentro del éter daba como resultado una deriva del éter, desplazando el campo electromagnético, lo que explica la falta de velocidad del observador en relación con él. La transformación galileana había sido el proceso matemático utilizado para traducir las posiciones en un sistema de referencia a predicciones de posiciones en otro sistema de referencia, todas trazadas en coordenadas cartesianas , pero este proceso fue reemplazado por la transformación de Lorentz , modelada por el holandés Hendrik Lorentz [1853– 1928].
Sin embargo, en 1887, los experimentadores Michelson y Morley no lograron detectar la deriva del éter. Se planteó la hipótesis de que el movimiento hacia el éter también provocaba el acortamiento del éter, como se modela en la contracción de Lorentz . Se planteó la hipótesis de que el éter mantenía así el campo electromagnético de Maxwell alineado con el principio de invariancia galileana en todos los marcos de referencia inerciales , mientras que la teoría del movimiento de Newton se salvaba.
El físico teórico y filósofo austriaco Ernst Mach criticó el espacio absoluto postulado por Newton. El matemático Jules-Henri Poincaré (1854-1912) cuestionó incluso el tiempo absoluto. En 1905, Pierre Duhem publicó una crítica devastadora de los fundamentos de la teoría del movimiento de Newton. [16] También en 1905, Albert Einstein (1879-1955) publicó su teoría especial de la relatividad , explicando de nuevo tanto la invariancia del campo electromagnético como la invariancia galileana descartando todas las hipótesis relativas al éter, incluida la existencia del éter mismo. Refutando el marco de la teoría de Newton ( espacio absoluto y tiempo absoluto ), la relatividad especial se refiere al espacio relativo y al tiempo relativo , mediante los cuales la longitud se contrae y el tiempo se dilata a lo largo de la trayectoria de viaje de un objeto.
En 1908, el ex profesor de matemáticas de Einstein, Hermann Minkowski, modeló el espacio 3D junto con el eje 1D del tiempo tratando el eje temporal como una cuarta dimensión espacial (espaciotiempo 4D) y declaró la inminente desaparición de la separación del espacio y el tiempo. [17] Einstein inicialmente llamó a esto "conocimiento superfluo", pero luego utilizó el espacio-tiempo de Minkowski con gran elegancia en su teoría general de la relatividad , [18] extendiendo la invariancia a todos los marcos de referencia, ya sea que se perciban como inerciales o acelerados, y se lo atribuyó a Minkowski. , para entonces fallecido. La relatividad general reemplaza las coordenadas cartesianas con coordenadas gaussianas y reemplaza el espacio vacío pero euclidiano afirmado por Newton, atravesado instantáneamente por el vector de fuerza gravitacional hipotética de Newton (una acción instantánea a distancia ) con un campo gravitacional . El campo gravitacional es el propio espacio-tiempo de Minkowski , la topología 4D del éter de Einstein modelada sobre una variedad de Lorentz que se "curva" geométricamente, según el tensor de curvatura de Riemann . El concepto de gravedad de Newton: "dos masas se atraen" fue reemplazado por el argumento geométrico: "la masa transforma las curvaturas del espacio-tiempo y las partículas con masa en caída libre se mueven a lo largo de una curva geodésica en el espacio-tiempo" ( la geometría de Riemann ya existía antes de la década de 1850, por los matemáticos Carl Friedrich Gauss y Bernhard Riemann en busca de geometría intrínseca y geometría no euclidiana), en las proximidades de la masa o la energía. (Bajo la relatividad especial, un caso especial de la relatividad general, incluso la energía sin masa ejerce un efecto gravitacional mediante su equivalencia de masa "curvando" localmente la geometría de las cuatro dimensiones unificadas del espacio y el tiempo).
Otro desarrollo revolucionario del siglo XX fue la teoría cuántica , que surgió de las contribuciones fundamentales de Max Planck (1856-1947) (sobre la radiación del cuerpo negro ) y el trabajo de Einstein sobre el efecto fotoeléctrico . En 1912, el matemático Henri Poincaré publicó Sur la théorie des quanta . [19] [20] En este artículo presentó la primera definición no ingenua de cuantificación. El desarrollo de la física cuántica temprana siguió a un marco heurístico ideado por Arnold Sommerfeld (1868-1951) y Niels Bohr (1885-1962), pero pronto fue reemplazado por la mecánica cuántica desarrollada por Max Born (1882-1970), Werner Heisenberg. (1901–1976), Paul Dirac (1902–1984), Erwin Schrödinger (1887–1961), Satyendra Nath Bose (1894–1974) y Wolfgang Pauli (1900–1958). Este marco teórico revolucionario se basa en una interpretación probabilística de estados, evolución y mediciones en términos de operadores autoadjuntos en un espacio vectorial de dimensión infinita. Eso se llama espacio de Hilbert (introducido por los matemáticos David Hilbert (1862-1943), Erhard Schmidt (1876-1959) y Frigyes Riesz (1880-1956) en busca de la generalización del espacio euclidiano y el estudio de ecuaciones integrales), y definido rigurosamente dentro la versión axiomática moderna de John von Neumann en su célebre libro Mathematical Foundations of Quantum Mechanics , donde construyó una parte relevante del análisis funcional moderno sobre los espacios de Hilbert, la teoría espectral (introducida por David Hilbert , quien investigó formas cuadráticas con infinitas variables). Muchos años después se supo que su teoría espectral estaba relacionada con el espectro del átomo de hidrógeno, lo que le sorprendió especialmente. Paul Dirac utilizó construcciones algebraicas para producir un modelo relativista para el electrón , prediciendo su momento magnético y la existencia de su antipartícula, el positrón .
Entre los contribuyentes destacados a la física matemática del siglo XX se incluyen (ordenados por fecha de nacimiento):
{{cite web}}: CS1 maint: archived copy as title (link)
Medios relacionados con la física matemática en Wikimedia Commons