Número complejo

Número con una parte real y una imaginaria

Un número complejo se puede representar visualmente como un par de números ( a ,  b ) que forman un vector en un diagrama llamado diagrama de Argand , que representa el plano complejo . Re es el eje real, Im es el eje imaginario e i es la " unidad imaginaria ", que satisface i ² = −1 .

En matemáticas , un número complejo es un elemento de un sistema numérico que extiende los números reales con un elemento específico denominado i , llamado unidad imaginaria y que satisface la ecuación ; todo número complejo se puede expresar en la forma , donde a y b son números reales. Como ningún número real satisface la ecuación anterior, René Descartes llamó a i un número imaginario . Para el número complejo , a se llama unidad imaginaria . ${\displaystyle i^{2}=-1}$ ${\displaystyle a+bi}$ ${\displaystyle a+bi}$ parte real , ybse llamaparte imaginaria . El conjunto de números complejos se denota por cualquiera de los símboloso C. A pesar de la nomenclatura histórica, los números complejos "imaginarios" tienen unamatemáticatan firme como la de los números reales, y son herramientas fundamentales en la descripción científica del mundo natural.^[1][2] ${\displaystyle \mathbb {C} }$

Los números complejos permiten soluciones a todas las ecuaciones polinómicas , incluso aquellas que no tienen solución en números reales. Más precisamente, el teorema fundamental del álgebra afirma que toda ecuación polinómica no constante con coeficientes reales o complejos tiene una solución que es un número complejo. Por ejemplo, la ecuación no tiene solución real, porque el cuadrado de un número real no puede ser negativo, pero tiene las dos soluciones complejas no reales y . ${\displaystyle (x+1)^{2}=-9}$ ${\displaystyle -1+3i}$ ${\displaystyle -1-3i}$

La suma, resta y multiplicación de números complejos se pueden definir de forma natural utilizando la regla junto con las leyes asociativa , conmutativa y distributiva . Todo número complejo distinto de cero tiene un inverso multiplicativo . Esto hace que los números complejos sean un campo con los números reales como subcampo. ${\displaystyle i^{2}=-1}$

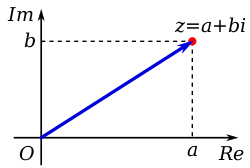
Los números complejos también forman un espacio vectorial real de dimensión dos , con como base estándar . Esta base estándar convierte a los números complejos en un plano cartesiano , llamado plano complejo . Esto permite una interpretación geométrica de los números complejos y sus operaciones, y a la inversa, algunos objetos y operaciones geométricas pueden expresarse en términos de números complejos. Por ejemplo, los números reales forman la línea real , que se representa como el eje horizontal del plano complejo, mientras que los múltiplos reales de son el eje vertical. Un número complejo también puede definirse por sus coordenadas polares geométricas : el radio se denomina valor absoluto del número complejo, mientras que el ángulo desde el eje real positivo se denomina argumento del número complejo. Los números complejos de valor absoluto uno forman el círculo unitario . Sumar un número complejo fijo a todos los números complejos define una traslación en el plano complejo, y multiplicar por un número complejo fijo es una semejanza centrada en el origen (dilatando por el valor absoluto y rotando por el argumento). La operación de conjugación compleja es la simetría de reflexión con respecto al eje real. ${\displaystyle \{1,i\}}$ ${\displaystyle i}$

Los números complejos forman una estructura rica que es simultáneamente un campo algebraicamente cerrado , un álgebra conmutativa sobre los reales y un espacio vectorial euclidiano de dimensión dos.

Definición y operaciones básicas

Varios números complejos representados en el plano complejo.

Un número complejo es una expresión de la forma a + bi , donde a y b son números reales , e i es un símbolo abstracto, la llamada unidad imaginaria , cuyo significado se explicará más adelante. Por ejemplo, 2 + 3 i es un número complejo. ^[3]

Para un número complejo a + bi , el número real a se llama su parte real , y el número real b (no el número complejo bi ) es su parte imaginaria . ^{[4] [5]} La parte real de un número complejo z se denota Re( z ) , , o ; la parte imaginaria es Im( z ) , , o : por ejemplo, , . ${\displaystyle {\mathcal {Re}}(z)}$ ${\displaystyle {\mathfrak {R}}(z)}$ ${\displaystyle {\mathcal {Im}}(z)}$ ${\displaystyle {\mathfrak {I}}(z)}$ ${\textstyle \operatorname {Re} (2+3i)=2}$ ${\displaystyle \operatorname {Im} (2+3i)=3}$

Un número complejo z puede identificarse con el par ordenado de números reales , que pueden interpretarse como coordenadas de un punto en un plano euclidiano con coordenadas estándar, que entonces se denomina plano complejo o diagrama de Argand , ^{[6] [a]} . ^[7] El eje horizontal se utiliza generalmente para mostrar la parte real, con valores crecientes hacia la derecha, y la parte imaginaria marca el eje vertical, con valores crecientes hacia arriba. ${\displaystyle (\Re (z),\Im (z))}$

Un número complejo z , como un punto (negro) y su vector de posición (azul).

Un número real a puede considerarse un número complejo a + 0 i , cuya parte imaginaria es 0. Un número puramente imaginario bi es un número complejo 0 + bi , cuya parte real es cero. Al igual que con los polinomios, es común escribir a + 0 i = a , 0 + bi = bi y a + (− b ) i = a − bi ; por ejemplo, 3 + (−4) i = 3 − 4 i .

El conjunto de todos los números complejos se denota por ( negrita pizarra ) o C (negrita vertical). ${\displaystyle \mathbb {C} }$

En algunas disciplinas como el electromagnetismo y la ingeniería eléctrica , se utiliza j en lugar de i , ya que i frecuentemente representa la corriente eléctrica , ^{[8] [9]} y los números complejos se escriben como a + bj o a + jb .

Suma y resta

La suma de dos números complejos se puede realizar geométricamente construyendo un paralelogramo.

Dos números complejos y se suman sumando por separado sus partes reales e imaginarias. Es decir: ${\displaystyle a=x+yi}$ ${\displaystyle b=u+vi}$

$${\displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}$$De manera similar, la resta se puede realizar como $${\displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}$$

La adición se puede visualizar geométricamente de la siguiente manera: la suma de dos números complejos a y b , interpretados como puntos en el plano complejo, es el punto obtenido al construir un paralelogramo a partir de los tres vértices O , y los puntos de las flechas rotuladas a y b (siempre que no estén sobre una recta). Equivalentemente, llamando a estos puntos A , B , respectivamente y al cuarto punto del paralelogramo X los triángulos OAB y XBA son congruentes .

Multiplicación

El producto de dos números complejos se calcula de la siguiente manera:

${\displaystyle (a+bi)\cdot (c+di)=ac-bd+(ad+bc)i.}$

Por ejemplo, en particular, esto incluye como caso especial la fórmula fundamental ${\displaystyle (3+2i)(4-i)=3\cdot 4-(2\cdot (-1))+(3\cdot (-1)+2\cdot 4)i=14+5i.}$

${\displaystyle i^{2}=i\cdot i=-1.}$

Esta fórmula distingue al número complejo i de cualquier número real, ya que el cuadrado de cualquier número real (negativo o positivo) es siempre un número real no negativo.

Con esta definición de multiplicación y adición, las reglas conocidas para la aritmética de números racionales o reales continúan siendo válidas para los números complejos. Más precisamente, se cumplen la propiedad distributiva y las propiedades conmutativas (de la adición y la multiplicación). Por lo tanto, los números complejos forman una estructura algebraica conocida como cuerpo , de la misma manera que lo hacen los números racionales o reales. ^[10]

Conjugado complejo, valor absoluto y argumento

Representación geométrica de z y su conjugado z en el plano complejo.

El conjugado complejo del número complejo z = x + yi se define como ^[11] Algunos autores también lo denotan como . Geométricamente, z es la "reflexión" de z sobre el eje real. Conjugando dos veces se obtiene el número complejo original: Un número complejo es real si y solo si es igual a su propio conjugado. La operación unaria de tomar el conjugado complejo de un número complejo no se puede expresar aplicando solo sus operaciones básicas de suma, resta, multiplicación y división. ${\displaystyle {\overline {z}}=x-yi.}$ ${\displaystyle z^{*}}$ ${\displaystyle {\overline {\overline {z}}}=z.}$

El argumento φ y el módulo r ubican un punto en el plano complejo.

Para cualquier número complejo z = x + yi , el producto

${\displaystyle z\cdot {\overline {z}}=(x+iy)(x-iy)=x^{2}+y^{2}}$

es un número real no negativo . Esto permite definir el valor absoluto (o módulo o magnitud ) de z como la raíz cuadrada ^[12] Por el teorema de Pitágoras , es la distancia desde el origen hasta el punto que representa el número complejo z en el plano complejo. En particular, el círculo de radio uno alrededor del origen consiste precisamente en los números z tales que . Si es un número real, entonces : su valor absoluto como número complejo y como número real son iguales. $${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}.}$$ ${\displaystyle |z|}$ ${\displaystyle |z|=1}$ ${\displaystyle z=x=x+0i}$ ${\displaystyle |z|=|x|}$

Utilizando el conjugado, el recíproco de un número complejo distinto de cero se puede calcular como ${\displaystyle z=x+yi}$

$${\displaystyle {\frac {1}{z}}={\frac {\bar {z}}{z{\bar {z}}}}={\frac {\bar {z}}{|z|^{2}}}={\frac {x-yi}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i.}$$De manera más general, la división de un número complejo arbitrario por un número complejo distinto de cero es igual a Este proceso a veces se denomina " racionalización " del denominador (aunque el denominador en la expresión final podría ser un número real irracional), porque se parece al método para eliminar raíces de expresiones simples en un denominador. ^{[ cita requerida ]} ${\displaystyle w=u+vi}$ ${\displaystyle z=x+yi}$ $${\displaystyle {\frac {w}{z}}={\frac {w{\bar {z}}}{|z|^{2}}}={\frac {(u+vi)(x-iy)}{x^{2}+y^{2}}}={\frac {ux+vy}{x^{2}+y^{2}}}+{\frac {vx-uy}{x^{2}+y^{2}}}i.}$$

El argumento de z (a veces llamado la "fase" φ ) ^[7] es el ángulo del radio Oz con el eje real positivo, y se escribe como arg z , expresado en radianes en este artículo. El ángulo se define solo hasta sumar múltiplos enteros de , ya que una rotación de (o 360°) alrededor del origen deja todos los puntos en el plano complejo sin cambios. Una posible opción para especificar de forma única el argumento es exigir que esté dentro del intervalo , al que se hace referencia como el valor principal . ^[13] El argumento se puede calcular a partir de la forma rectangular x + yi por medio de la función arctan (tangente inversa). ^[14] ${\displaystyle 2\pi }$ ${\displaystyle 2\pi }$ ${\displaystyle (-\pi ,\pi ]}$

Forma polar

Multiplicación de 2 + i (triángulo azul) y 3 + i (triángulo rojo). El triángulo rojo se gira para que coincida con el vértice del triángulo azul (la suma de ambos ángulos en los términos φ ₁ + φ ₂ en la ecuación) y se estira por la longitud de la hipotenusa del triángulo azul (la multiplicación de ambos radios, según el término r ₁ r ₂ en la ecuación).

Para cualquier número complejo z , con valor absoluto y argumento , la ecuación ${\displaystyle r=|z|}$ ${\displaystyle \varphi }$

${\displaystyle z=r(\cos \varphi +i\sin \varphi )}$

se cumple. Esta identidad se denomina forma polar de z . A veces se abrevia como . En electrónica , se representa un fasor con amplitud r y fase φ en notación angular : ^[15] ${\textstyle z=r\operatorname {\mathrm {cis} } \varphi }$ $${\displaystyle z=r\angle \varphi .}$$

Si se dan dos números complejos en forma polar, es decir, z ₁ = r ₁ (cos  φ ₁ + i  sen  φ ₁ ) y z ₂ = r ₂ (cos  φ ₂ + i  sen  φ ₂ ) , el producto y la división se pueden calcular como (Estas son una consecuencia de las identidades trigonométricas para la función seno y coseno). En otras palabras, los valores absolutos se multiplican y los argumentos se suman para obtener la forma polar del producto. La imagen de la derecha ilustra la multiplicación de Debido a que la parte real e imaginaria de 5 + 5 i son iguales, el argumento de ese número es 45 grados, o π /4 (en radianes ). Por otro lado, también es la suma de los ángulos en el origen de los triángulos rojo y azul son arctan (1/3) y arctan (1/2), respectivamente. Por lo tanto, la fórmula es válida. Como la función arctan se puede aproximar de manera muy eficiente, se utilizan fórmulas como ésta (conocidas como fórmulas de tipo Machin ) para aproximaciones de alta precisión de π . ^{[ cita requerida ]} $${\displaystyle z_{1}z_{2}=r_{1}r_{2}(\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})).}$$ $${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\left(\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right),{\text{if }}z_{2}\neq 0.}$$ $${\displaystyle (2+i)(3+i)=5+5i.}$$ $${\displaystyle {\frac {\pi }{4}}=\arctan \left({\frac {1}{2}}\right)+\arctan \left({\frac {1}{3}}\right)}$$

Poderes y raíces

La n -ésima potencia de un número complejo se puede calcular utilizando la fórmula de De Moivre , que se obtiene aplicando repetidamente la fórmula anterior para el producto: Por ejemplo, las primeras potencias de la unidad imaginaria i son . $${\displaystyle z^{n}=\underbrace {z\cdot \dots \cdot z} _{n{\text{ factors}}}=(r(\cos \varphi +i\sin \varphi ))^{n}=r^{n}\,(\cos n\varphi +i\sin n\varphi ).}$$ ${\displaystyle i,i^{2}=-1,i^{3}=-i,i^{4}=1,i^{5}=i,\dots }$

Representación geométrica de las raíces 2.ª a 6.ª de un número complejo z , en forma polar re ^iφ  donde r = | z  | y φ = arg z . Si z es real, φ = 0 o π . Las raíces principales se muestran en negro.

Las raíces n n -ésimas de un número complejo z están dadas por para 0 ≤ k ≤ n − 1 . (Aquí está la raíz n -ésima (positiva) habitual del número real positivo r .) Como el seno y el coseno son periódicos, otros valores enteros de k no dan otros valores. Para cualquier , hay, en particular, n raíces n -ésimas complejas distintas . Por ejemplo, hay 4 raíces cuartas de 1, a saber: $${\displaystyle z^{1/n}={\sqrt[{n}]{r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi }{n}}\right)\right)}$$ ${\displaystyle {\sqrt[{n}]{r}}}$ ${\displaystyle z\neq 0}$

${\displaystyle z_{1}=1,z_{2}=i,z_{3}=-1,z_{4}=-i.}$

En general, no hay una forma natural de distinguir una raíz n- ésima compleja particular de un número complejo. (Esto contrasta con las raíces de un número real positivo x , que tiene una única raíz n -ésima real positiva , a la que se suele denominar raíz n - ésima de x ). Se hace referencia a esta situación diciendo que la raíz n -ésima es una función de valor n de z .

Teorema fundamental del álgebra

El teorema fundamental del álgebra , de Carl Friedrich Gauss y Jean le Rond d'Alembert , establece que para cualesquiera números complejos (llamados coeficientes ) a ₀ , ...,  a _n , la ecuación tiene al menos una solución compleja z , siempre que al menos uno de los coeficientes superiores a ₁ , ...,  a _n sea distinto de cero. ^[16] Esta propiedad no se cumple para el cuerpo de los números racionales (el polinomio x ² − 2 no tiene raíz racional, porque √2 no es un número racional) ni para los números reales (el polinomio x ² + 4 no tiene raíz real, porque el cuadrado de x es positivo para cualquier número real x ). $${\displaystyle a_{n}z^{n}+\dotsb +a_{1}z+a_{0}=0}$$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$

Por este hecho, se le denomina cuerpo algebraicamente cerrado . Es una piedra angular de diversas aplicaciones de los números complejos, como se detalla más adelante. Existen diversas demostraciones de este teorema, ya sea por métodos analíticos como el teorema de Liouville , o topológicos como el número de vueltas , o una demostración que combina la teoría de Galois y el hecho de que cualquier polinomio real de grado impar tiene al menos una raíz real. ${\displaystyle \mathbb {C} }$

Historia

La solución en radicales (sin funciones trigonométricas ) de una ecuación cúbica general , cuando sus tres raíces son números reales, contiene las raíces cuadradas de números negativos , una situación que no se puede rectificar mediante factorización con la ayuda de la prueba de la raíz racional , si la cúbica es irreducible ; este es el llamado casus irreducibilis ("caso irreducible"). Este enigma llevó al matemático italiano Gerolamo Cardano a concebir los números complejos alrededor de 1545 en su Ars Magna , ^[17] aunque su comprensión era rudimentaria; además, más tarde describió los números complejos como "tan sutiles como inútiles". ^[18] Cardano usó números imaginarios, pero describió su uso como una "tortura mental". ^[19] Esto fue anterior al uso del plano complejo gráfico. Cardano y otros matemáticos italianos, en particular Scipione del Ferro , crearon en el siglo XVI un algoritmo para resolver ecuaciones cúbicas que, por lo general, tenían una solución real y dos soluciones que contenían un número imaginario. Como ignoraban las respuestas con números imaginarios, Cardano las consideró inútiles. ^[20]

El trabajo sobre el problema de los polinomios generales condujo finalmente al teorema fundamental del álgebra , que demuestra que, con los números complejos, existe una solución para cada ecuación polinómica de grado uno o superior. Los números complejos forman, por tanto, un campo algebraicamente cerrado , donde cualquier ecuación polinómica tiene una raíz .

Muchos matemáticos contribuyeron al desarrollo de los números complejos. Las reglas para la suma, resta, multiplicación y extracción de raíces de números complejos fueron desarrolladas por el matemático italiano Rafael Bombelli . ^[21] Un formalismo más abstracto para los números complejos fue desarrollado por el matemático irlandés William Rowan Hamilton , quien extendió esta abstracción a la teoría de los cuaterniones . ^[22]

La primera referencia fugaz a las raíces cuadradas de números negativos tal vez se pueda decir que ocurre en el trabajo del matemático griego Herón de Alejandría en el siglo I d.C. , donde en su Stereometrica consideró, aparentemente por error, el volumen de un tronco de pirámide imposible para llegar al término en sus cálculos, que hoy se simplificaría a . ^[b] Las cantidades negativas no se concibieron en las matemáticas helenísticas y Herón simplemente las reemplazó por su valor positivo ^[24] ${\displaystyle {\sqrt {81-144}}}$ ${\displaystyle {\sqrt {-63}}=3i{\sqrt {7}}}$ ${\displaystyle {\sqrt {144-81}}=3{\sqrt {7}}.}$

El impulso para estudiar los números complejos como un tema en sí mismo surgió por primera vez en el siglo XVI cuando los matemáticos italianos ( Niccolò Fontana Tartaglia y Gerolamo Cardano ) descubrieron soluciones algebraicas para las raíces de polinomios cúbicos y cuárticos . Pronto se comprendió (pero se demostró mucho más tarde) ^[25] que estas fórmulas, incluso si uno solo estaba interesado en soluciones reales, a veces requerían la manipulación de raíces cuadradas de números negativos. De hecho, se demostró más tarde que el uso de números complejos es inevitable cuando las tres raíces son reales y distintas. ^[c] Sin embargo, la fórmula general todavía se puede utilizar en este caso, con cierto cuidado para lidiar con la ambigüedad resultante de la existencia de tres raíces cúbicas para números complejos distintos de cero. Rafael Bombelli fue el primero en abordar explícitamente estas soluciones aparentemente paradójicas de ecuaciones cúbicas y desarrolló las reglas para la aritmética compleja, tratando de resolver estos problemas.

El término "imaginario" para estas cantidades fue acuñado por René Descartes en 1637, quien se esforzó por enfatizar su naturaleza irreal: ^[26]

... a veces sólo imaginaria, es decir uno puede imaginar tantas como dije en cada ecuación, pero a veces no existe ninguna cantidad que coincida con la que imaginamos.
[ ... quelquefois solo imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en cada ecuación, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imaginar. ]

Otra fuente de confusión fue que la ecuación parecía ser caprichosamente inconsistente con la identidad algebraica , que es válida para números reales no negativos a y b , y que también se usaba en cálculos con números complejos con uno de a , b positivo y el otro negativo. El uso incorrecto de esta identidad en el caso en que tanto a como b son negativos, y la identidad relacionada , incluso atormentó a Leonhard Euler . Esta dificultad eventualmente llevó a la convención de usar el símbolo especial i en lugar de para protegerse contra este error. ^{[ cita requerida ]} Aun así, Euler consideró natural introducir a los estudiantes a los números complejos mucho antes de lo que lo hacemos hoy. En su libro de texto de álgebra elemental, Elementos de álgebra , introduce estos números casi de inmediato y luego los usa de manera natural a lo largo del libro. ${\displaystyle {\sqrt {-1}}^{2}={\sqrt {-1}}{\sqrt {-1}}=-1}$ ${\displaystyle {\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}}$ ${\textstyle {\frac {1}{\sqrt {a}}}={\sqrt {\frac {1}{a}}}}$ ${\displaystyle {\sqrt {-1}}}$

En el siglo XVIII, los números complejos se empezaron a utilizar más ampliamente, ya que se observó que la manipulación formal de expresiones complejas podía utilizarse para simplificar los cálculos que involucraban funciones trigonométricas. Por ejemplo, en 1730, Abraham de Moivre observó que las identidades que relacionaban las funciones trigonométricas de un múltiplo entero de un ángulo con las potencias de las funciones trigonométricas de ese ángulo podían reexpresarse mediante la siguiente fórmula de De Moivre :

$${\displaystyle (\cos \theta +i\sin \theta )^{n}=\cos n\theta +i\sin n\theta .}$$

La fórmula de Euler relaciona la función exponencial compleja de un argumento imaginario, que puede considerarse como la descripción de un movimiento circular uniforme en el plano complejo, con las funciones coseno y seno, geométricamente sus proyecciones sobre los ejes real e imaginario, respectivamente.

En 1748, Euler fue más allá y obtuvo la fórmula de Euler para el análisis complejo : ^[27]

$${\displaystyle e^{i\theta }=\cos \theta +i\sin \theta }$$

manipulando formalmente series de potencias complejas y observó que esta fórmula podía usarse para reducir cualquier identidad trigonométrica a identidades exponenciales mucho más simples.

La idea de un número complejo como un punto en el plano complejo (arriba) fue descrita por primera vez por el matemático danés - noruego Caspar Wessel en 1799, ^[28] aunque había sido anticipada ya en 1685 en el Tratado de álgebra de Wallis . ^[29]

Las memorias de Wessel aparecieron en las Actas de la Academia de Copenhague , pero pasaron prácticamente desapercibidas. En 1806, Jean-Robert Argand publicó de forma independiente un panfleto sobre números complejos y proporcionó una prueba rigurosa del teorema fundamental del álgebra . ^[30] Carl Friedrich Gauss había publicado anteriormente una prueba esencialmente topológica del teorema en 1797, pero expresó sus dudas en ese momento sobre "la verdadera metafísica de la raíz cuadrada de −1". ^[31] No fue hasta 1831 que superó estas dudas y publicó su tratado sobre los números complejos como puntos en el plano, ^[32] estableciendo en gran medida la notación y la terminología modernas: ^[33]

Si antes se contemplaba este tema desde un punto de vista erróneo y se encontraba, por tanto, con una misteriosa oscuridad, esto se debe en gran parte a una terminología torpe. Si no se hubieran llamado unidades +1, -1, positivas, negativas o imaginarias (o incluso imposibles), sino, por ejemplo, unidades directas, inversas o laterales, difícilmente se habría podido hablar de tal oscuridad. ${\displaystyle {\sqrt {-1}}}$

A principios del siglo XIX, otros matemáticos descubrieron independientemente la representación geométrica de los números complejos: Buée, ^{[34] [35]} Mourey , ^[36] Warren, ^{[37] [38] [39]} Français y su hermano, Bellavitis . ^{[40] [41]}

El matemático inglés GH Hardy comentó que Gauss fue el primer matemático en utilizar números complejos "de una manera realmente segura y científica", aunque matemáticos como el noruego Niels Henrik Abel y Carl Gustav Jacob Jacobi necesariamente los utilizaban de manera rutinaria antes de que Gauss publicara su tratado de 1831. ^[42]

Augustin-Louis Cauchy y Bernhard Riemann juntos llevaron las ideas fundamentales del análisis complejo a un alto grado de perfeccionamiento, comenzando alrededor de 1825 en el caso de Cauchy.

Los términos comunes utilizados en la teoría se deben principalmente a los fundadores. Argand llamó a cos φ + i sen φ el factor de dirección y al módulo ; ^{[d] [43]} Cauchy (1821) llamó a cos φ + i sen φ la forma reducida (l'expression réduite) ^[44] y aparentemente introdujo el término argumento ; Gauss usó i para , ^[e] introdujo el término número complejo para a + bi , ^[f] y llamó a ² + b ² la norma . ^[g] La expresión coeficiente de dirección , a menudo utilizada para cos φ + i sen φ , se debe a Hankel (1867), ^[48] y valor absoluto, para módulo, se debe a Weierstrass. ${\displaystyle r={\sqrt {a^{2}+b^{2}}}}$ ${\displaystyle {\sqrt {-1}}}$

Entre los autores clásicos posteriores que han escrito sobre la teoría general se encuentran Richard Dedekind , Otto Hölder , Felix Klein , Henri Poincaré , Hermann Schwarz , Karl Weierstrass y muchos otros. A principios del siglo XX se inició un importante trabajo (incluida una sistematización) en cálculo multivariante complejo. Wilhelm Wirtinger logró importantes resultados en 1927.

Aspectos algebraicos abstractos

Si bien las definiciones de bajo nivel anteriores, incluidas la suma y la multiplicación, describen con precisión los números complejos, existen otros enfoques equivalentes que revelan la estructura algebraica abstracta de los números complejos de manera más inmediata.

La construcción como campo cociente

Un enfoque para esto es a través de polinomios , es decir, expresiones de la forma donde los coeficientes a ₀ , ...,  a _n son números reales. El conjunto de todos esos polinomios se denota por . Dado que las sumas y productos de polinomios son nuevamente polinomios, este conjunto forma un anillo conmutativo , llamado el anillo polinomial (sobre los reales). A cada polinomio p , se le puede asignar el número complejo , es decir, el valor obtenido al establecer . Esto define una función ${\displaystyle \mathbb {C} }$ $${\displaystyle p(X)=a_{n}X^{n}+\dotsb +a_{1}X+a_{0},}$$ ${\displaystyle \mathbb {R} [X]}$ ${\displaystyle \mathbb {R} [X]}$ ${\displaystyle p(i)=a_{n}i^{n}+\dotsb +a_{1}i+a_{0}}$ ${\displaystyle X=i}$

${\displaystyle \mathbb {R} [X]\to \mathbb {C} }$

Esta función es sobreyectiva ya que todo número complejo puede obtenerse de la siguiente manera: la evaluación de un polinomio lineal en es . Sin embargo, la evaluación del polinomio en i es 0, ya que Este polinomio es irreducible , es decir, no puede escribirse como un producto de dos polinomios lineales. Los hechos básicos del álgebra abstracta implican entonces que el núcleo de la función anterior es un ideal generado por este polinomio, y que el cociente por este ideal es un cuerpo, y que existe un isomorfismo ${\displaystyle a+bX}$ ${\displaystyle X=i}$ ${\displaystyle a+bi}$ ${\displaystyle X^{2}+1}$ ${\displaystyle i^{2}+1=0.}$

${\displaystyle \mathbb {R} [X]/(X^{2}+1){\stackrel {\cong }{\to }}\mathbb {C} }$

entre el anillo cociente y . Algunos autores toman esto como la definición de . ^[49] ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Aceptar que es algebraicamente cerrado, porque es una extensión algebraica de en este enfoque, es por lo tanto el cierre algebraico de ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} .}$

Representación matricial de números complejos

Los números complejos a + bi también se pueden representar mediante matrices de 2 × 2 que tienen la forma Aquí las entradas a y b son números reales. Como la suma y el producto de dos matrices de este tipo tiene nuevamente esta forma, estas matrices forman un subanillo del anillo de matrices de 2 × 2 . $${\displaystyle {\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}.}$$

Un cálculo simple muestra que la función es un isomorfismo de anillo del cuerpo de números complejos al anillo de estas matrices, lo que demuestra que estas matrices forman un cuerpo. Este isomorfismo asocia el cuadrado del valor absoluto de un número complejo con el determinante de la matriz correspondiente, y el conjugado de un número complejo con la transpuesta de la matriz. $${\displaystyle a+ib\mapsto {\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}}$$

La descripción geométrica de la multiplicación de números complejos también puede expresarse en términos de matrices de rotación utilizando esta correspondencia entre números complejos y dichas matrices. La acción de la matriz sobre un vector ( x , y ) corresponde a la multiplicación de x + iy por a + ib . En particular, si el determinante es 1 , existe un número real t tal que la matriz tiene la forma

$${\displaystyle {\begin{pmatrix}\cos t&-\sin t\\\sin t&\;\;\cos t\end{pmatrix}}.}$$En este caso, la acción de la matriz sobre los vectores y la multiplicación por el número complejo son ambas la rotación del ángulo t . ${\displaystyle \cos t+i\sin t}$

Análisis complejo

El estudio de funciones de una variable compleja se conoce como análisis complejo y tiene un enorme uso práctico en matemáticas aplicadas , así como en otras ramas de las matemáticas. A menudo, las demostraciones más naturales de los enunciados del análisis real o incluso de la teoría de números emplean técnicas del análisis complejo (véase el teorema de los números primos como ejemplo).

Un gráfico de coloración de dominio de la función ⁠( z ² − 1)( z − 2 − yo ) ²/yo^​​​⁠ . Los puntos más oscuros marcan módulos cercanos a cero, los puntos más brillantes están más alejados del origen. El color codifica el argumento. La función tiene ceros para ±1, (2 + i ) y polos en ${\displaystyle \pm {\sqrt {-2-2i}}.}$

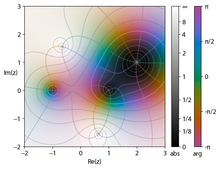
A diferencia de las funciones reales, que comúnmente se representan como gráficos bidimensionales, las funciones complejas tienen gráficos de cuatro dimensiones y pueden ilustrarse de manera útil codificando con colores un gráfico tridimensional para sugerir cuatro dimensiones, o animando la transformación dinámica del plano complejo de la función compleja.

Convergencia

Ilustración del comportamiento de la secuencia para tres valores diferentes de z (todos con el mismo argumento): para la secuencia converge a 0 (espiral interna), mientras que diverge para (espiral externa). ${\displaystyle z^{n}}$ ${\displaystyle |z|<1}$ ${\displaystyle |z|>1}$

Las nociones de series convergentes y funciones continuas en el análisis (real) tienen análogos naturales en el análisis complejo. Se dice que una secuencia de números complejos converge si y solo si lo hacen sus partes reales e imaginarias. Esto es equivalente a la (ε, δ)-definición de límites , donde el valor absoluto de los números reales se reemplaza por el de los números complejos. Desde un punto de vista más abstracto, , dotado de la métrica es un espacio métrico completo , que incluye notablemente la desigualdad triangular para dos números complejos cualesquiera z ₁ y z ₂ . ${\displaystyle \mathbb {C} }$ $${\displaystyle \operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|}$$ $${\displaystyle |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|}$$

exponencial complejo

Ilustración de la función exponencial compleja que mapea el plano complejo, w = exp ⁡( z ). El plano izquierdo muestra una malla cuadrada con un tamaño de malla de 1, con los tres números complejos 0, 1 e i resaltados. Los dos rectángulos (en magenta y verde) están mapeados a segmentos circulares, mientras que las líneas paralelas al eje x están mapeadas a rayos que emanan del origen, pero que no lo contienen. Las líneas paralelas al eje y están mapeadas a círculos.

Al igual que en el análisis real, esta noción de convergencia se utiliza para construir una serie de funciones elementales : la función exponencial exp z , también escrita e ^z , se define como la serie infinita , que se puede demostrar que converge para cualquier z : Por ejemplo, es el número de Euler . La fórmula de Euler establece: para cualquier número real φ . Esta fórmula es una consecuencia rápida de los hechos básicos generales sobre las series de potencias convergentes y las definiciones de las funciones involucradas como series de potencias. Como caso especial, esto incluye la identidad de Euler $${\displaystyle \exp z:=1+z+{\frac {z^{2}}{2\cdot 1}}+{\frac {z^{3}}{3\cdot 2\cdot 1}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.}$$ ${\displaystyle \exp(1)}$ ${\displaystyle e\approx 2.718}$ $${\displaystyle \exp(i\varphi )=\cos \varphi +i\sin \varphi }$$ $${\displaystyle \exp(i\pi )=-1.}$$

Logaritmo complejo

La función exponencial asigna números complejos z que difieren en un múltiplo de al mismo número complejo w . ${\displaystyle 2\pi i}$

Para cualquier número real positivo t , existe un único número real x tal que . Esto conduce a la definición del logaritmo natural como la inversa de la función exponencial. La situación es diferente para los números complejos, ya que ${\displaystyle \exp(x)=t}$ ${\displaystyle \ln \colon \mathbb {R} ^{+}\to \mathbb {R} ;x\mapsto \ln x}$

${\displaystyle \exp(z+2\pi i)=\exp z\exp(2\pi i)=\exp z}$

por la ecuación funcional y la identidad de Euler. Por ejemplo, e ^iπ = e ^{3 iπ} = −1 , por lo que tanto iπ como 3 iπ son valores posibles para el logaritmo complejo de −1 .

En general, dado cualquier número complejo w distinto de cero , cualquier número z resuelve la ecuación

${\displaystyle \exp z=w}$

se llama logaritmo complejo de w , denotado . Se puede demostrar que estos números satisfacen donde arg es el argumento definido anteriormente, y ln el logaritmo natural (real) . Como arg es una función multivaluada , única solo hasta un múltiplo de 2 π , log también es multivaluado. El valor principal de log se toma a menudo restringiendo la parte imaginaria al intervalo (− π , π ] . Esto lleva a que el logaritmo complejo sea una función biyectiva que toma valores en la franja (que se denota en la ilustración anterior) ${\displaystyle \log w}$ $${\displaystyle z=\log w=\ln |w|+i\arg w,}$$ ${\displaystyle \mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right]}$ ${\displaystyle S_{0}}$ $${\displaystyle \ln \colon \;\mathbb {C} ^{\times }\;\to \;\;\;\mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right].}$$

Si no es un número real no positivo (sea positivo o no real), el valor principal resultante del logaritmo complejo se obtiene con − π < φ < π . Es una función analítica fuera de los números reales negativos, pero no se puede prolongar a una función que sea continua en cualquier número real negativo , donde el valor principal es ln z = ln(− z ) + iπ . ^[h] ${\displaystyle z\in \mathbb {C} \setminus \left(-\mathbb {R} _{\geq 0}\right)}$ ${\displaystyle z\in -\mathbb {R} ^{+}}$

La exponenciación compleja z ^ω se define como y es multivaluada, excepto cuando ω es un entero. Para ω = 1 / n , para algún número natural n , esto recupera la no unicidad de las raíces n mencionadas anteriormente. Si z > 0 es real (y ω un número complejo arbitrario), uno tiene una opción preferida de , el logaritmo real, que se puede usar para definir una función exponencial preferida. $${\displaystyle z^{\omega }=\exp(\omega \ln z),}$$ ${\displaystyle \ln x}$

Los números complejos, a diferencia de los números reales, en general no satisfacen las identidades de potencia y logaritmo sin modificar, en particular cuando se los trata ingenuamente como funciones de un solo valor; consulte el fallo de las identidades de potencia y logaritmo . Por ejemplo, no satisfacen Ambos lados de la ecuación son multivaluados por la definición de exponenciación compleja dada aquí, y los valores de la izquierda son un subconjunto de los de la derecha. $${\displaystyle a^{bc}=\left(a^{b}\right)^{c}.}$$

Seno y coseno complejos

Las series que definen las funciones trigonométricas reales seno y coseno , así como las funciones hiperbólicas senh y cosh, también se trasladan a argumentos complejos sin cambios. Para las otras funciones trigonométricas e hiperbólicas, como la tangente , las cosas son un poco más complicadas, ya que las series que las definen no convergen para todos los valores complejos. Por lo tanto, uno debe definirlas en términos de seno, coseno y exponencial, o, equivalentemente, utilizando el método de continuación analítica .

Funciones holomorfas

Gráfica de rueda de colores de la función sin(1/ z ) que es holomorfa excepto en z = 0, que es una singularidad esencial de esta función. Las partes blancas en el interior se refieren a números que tienen valores absolutos grandes.

Una función → se llama holomorfa o compleja diferenciable en un punto si el límite ${\displaystyle f:\mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle z_{0}}$

${\displaystyle \lim _{z\to z_{0}}{f(z)-f(z_{0}) \over z-z_{0}}}$

existe (en cuyo caso se denota por ). Esto imita la definición de funciones diferenciables reales, excepto que todas las cantidades son números complejos. En términos generales, la libertad de aproximación en diferentes direcciones impone una condición mucho más fuerte que ser diferenciable (real). Por ejemplo, la función ${\displaystyle f'(z_{0})}$ ${\displaystyle z_{0}}$

${\displaystyle f(z)={\overline {z}}}$

es diferenciable como función , pero no es complejamente diferenciable. Una función diferenciable real es complejamente diferenciable si y solo si satisface las ecuaciones de Cauchy-Riemann , que a veces se abrevian como ${\displaystyle \mathbb {R} ^{2}\to \mathbb {R} ^{2}}$

${\displaystyle {\frac {\partial f}{\partial {\overline {z}}}}=0.}$

El análisis complejo muestra algunas características que no son evidentes en el análisis real. Por ejemplo, el teorema de identidad afirma que dos funciones holomorfas f y g concuerdan si concuerdan en un subconjunto abierto arbitrariamente pequeño de . Las funciones meromorfas , funciones que pueden escribirse localmente como f ( z )/( z − z ₀ ) ⁿ con una función holomorfa f , aún comparten algunas de las características de las funciones holomorfas. Otras funciones tienen singularidades esenciales , como sin(1/ z ) en z = 0 . ${\displaystyle \mathbb {C} }$

Aplicaciones

Los números complejos tienen aplicaciones en muchas áreas científicas, entre ellas el procesamiento de señales , la teoría de control , el electromagnetismo , la dinámica de fluidos , la mecánica cuántica , la cartografía y el análisis de vibraciones . Algunas de estas aplicaciones se describen a continuación.

La conjugación compleja también se emplea en geometría inversa , una rama de la geometría que estudia reflexiones más generales que las que se producen alrededor de una línea. En el análisis de redes de circuitos eléctricos , la conjugación compleja se utiliza para hallar la impedancia equivalente cuando se busca el teorema de transferencia de potencia máxima .

Geometría

Formas

Tres puntos no colineales en el plano determinan la forma del triángulo . Ubicando los puntos en el plano complejo, esta forma de un triángulo puede expresarse mediante aritmética compleja como La forma de un triángulo permanecerá igual, cuando el plano complejo se transforma por traslación o dilatación (por una transformación afín ), correspondiente a la noción intuitiva de forma, y ​​describe la similitud . Por lo tanto, cada triángulo está en una clase de similitud de triángulos con la misma forma. ^[50] ${\displaystyle u,v,w}$ ${\displaystyle \{u,v,w\}}$ $${\displaystyle S(u,v,w)={\frac {u-w}{u-v}}.}$$ ${\displaystyle S}$ ${\displaystyle \{u,v,w\}}$

Geometría fractal

El conjunto de Mandelbrot con los ejes real e imaginario etiquetados.

El conjunto de Mandelbrot es un ejemplo popular de fractal formado en el plano complejo. Se define trazando cada posición en la que la iteración de la secuencia no diverge cuando se itera infinitamente. De manera similar, los conjuntos de Julia tienen las mismas reglas, excepto donde permanece constante. ${\displaystyle c}$ ${\displaystyle f_{c}(z)=z^{2}+c}$ ${\displaystyle c}$

Triángulos

Cada triángulo tiene una única elipse de Steiner : una elipse dentro del triángulo y tangente a los puntos medios de los tres lados del triángulo. Los focos de la elipse de Steiner de un triángulo se pueden encontrar de la siguiente manera, según el teorema de Marden : ^{[51] [52]} Denotemos los vértices del triángulo en el plano complejo como a = x _A + y _A i , b = x _B + y _B i , y c = x _C + y _C i . Escribamos la ecuación cúbica , tomemos su derivada e igualemos la derivada (cuadrática) a cero. El teorema de Marden dice que las soluciones de esta ecuación son los números complejos que denotan las ubicaciones de los dos focos de la elipse de Steiner. ${\displaystyle (x-a)(x-b)(x-c)=0}$

Teoría algebraica de números

Construcción de un pentágono regular utilizando regla y compás .

Como se mencionó anteriormente, cualquier ecuación polinómica no constante (en coeficientes complejos) tiene una solución en . A fortiori , lo mismo es cierto si la ecuación tiene coeficientes racionales. Las raíces de tales ecuaciones se llaman números algebraicos : son un objeto principal de estudio en la teoría de números algebraicos . En comparación con , la clausura algebraica de , que también contiene todos los números algebraicos, tiene la ventaja de ser fácilmente comprensible en términos geométricos. De esta manera, los métodos algebraicos se pueden usar para estudiar cuestiones geométricas y viceversa. Con métodos algebraicos, más específicamente aplicando la maquinaria de la teoría de campos al campo de números que contiene raíces de la unidad , se puede demostrar que no es posible construir un nonágono regular utilizando solo compás y regla , un problema puramente geométrico. ${\displaystyle \mathbb {C} }$ ${\displaystyle {\overline {\mathbb {Q} }}}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} }$

Otro ejemplo son los números enteros gaussianos , es decir, números de la forma x + iy , donde x e y son números enteros, que pueden utilizarse para clasificar sumas de cuadrados .

Teoría analítica de números

La teoría analítica de números estudia los números, a menudo enteros o racionales, aprovechando el hecho de que pueden considerarse como números complejos, en los que se pueden utilizar métodos analíticos. Esto se hace codificando la información de la teoría de números en funciones de valor complejo. Por ejemplo, la función zeta de Riemann ζ( s ) está relacionada con la distribución de números primos .

Integrales impropias

En los campos aplicados, los números complejos se utilizan a menudo para calcular ciertas integrales impropias de valor real , mediante funciones de valor complejo. Existen varios métodos para hacerlo; consulte métodos de integración de contornos .

Ecuaciones dinámicas

En ecuaciones diferenciales , es común encontrar primero todas las raíces complejas r de la ecuación característica de una ecuación diferencial lineal o sistema de ecuaciones y luego intentar resolver el sistema en términos de funciones base de la forma f ( t ) = e ^rt . De la misma manera, en ecuaciones en diferencias , se utilizan las raíces complejas r de la ecuación característica del sistema de ecuaciones en diferencias, para intentar resolver el sistema en términos de funciones base de la forma f ( t ) = r ^t .

Álgebra lineal

Dado que es algebraicamente cerrada, cualquier matriz cuadrada compleja no vacía tiene al menos un valor propio (complejo) . En comparación, las matrices reales no siempre tienen valores propios reales, por ejemplo , las matrices de rotación (para rotaciones del plano para ángulos distintos de 0° o 180°) no dejan una dirección fija y, por lo tanto, no tienen ningún valor propio real . La existencia de valores propios (complejos) y la consiguiente existencia de descomposición propia es una herramienta útil para calcular potencias matriciales y exponenciales matriciales . ${\displaystyle \mathbb {C} }$

Los números complejos a menudo generalizan conceptos concebidos originalmente en los números reales. Por ejemplo, la transpuesta conjugada generaliza la transpuesta , las matrices hermíticas generalizan las matrices simétricas y las matrices unitarias generalizan las matrices ortogonales .

En matemáticas aplicadas

Teoría del control

En la teoría de control , los sistemas se transforman a menudo del dominio del tiempo al dominio complejo de la frecuencia mediante la transformada de Laplace . Los ceros y polos del sistema se analizan luego en el plano complejo . Las técnicas de lugar de raíces , diagrama de Nyquist y diagrama de Nichols hacen uso del plano complejo.

En el método del lugar de las raíces, es importante que los ceros y los polos estén en los semiplanos izquierdo o derecho, es decir, que tengan una parte real mayor o menor que cero. Si un sistema lineal invariante en el tiempo (LTI) tiene polos que están

• En el semiplano derecho, será inestable .
• todo en el semiplano izquierdo, será estable ,
• en el eje imaginario, tendrá estabilidad marginal .

Si un sistema tiene ceros en el semiplano derecho, es un sistema de fase no mínima .

Análisis de señales

Los números complejos se utilizan en el análisis de señales y en otros campos para describir de manera conveniente las señales que varían periódicamente. Para funciones reales dadas que representan cantidades físicas reales, a menudo en términos de senos y cosenos, se consideran funciones complejas correspondientes cuyas partes reales son las cantidades originales. Para una onda sinusoidal de una frecuencia dada , el valor absoluto | z | de la z correspondiente es la amplitud y el argumento arg z es la fase .

Si se emplea el análisis de Fourier para escribir una señal dada de valor real como una suma de funciones periódicas, estas funciones periódicas a menudo se escriben como funciones de valor complejo de la forma

$${\displaystyle x(t)=\operatorname {Re} \{X(t)\}}$$

y

$${\displaystyle X(t)=Ae^{i\omega t}=ae^{i\phi }e^{i\omega t}=ae^{i(\omega t+\phi )}}$$

donde ω representa la frecuencia angular y el número complejo A codifica la fase y la amplitud como se explicó anteriormente.

Este uso también se extiende al procesamiento de señales digitales y al procesamiento de imágenes digitales , que utilizan versiones digitales del análisis de Fourier (y del análisis wavelet ) para transmitir, comprimir , restaurar y procesar de otro modo señales de audio digitales , imágenes fijas y señales de vídeo .

Otro ejemplo, relevante para las dos bandas laterales de modulación de amplitud de la radio AM, es:

$${\displaystyle {\begin{aligned}\cos((\omega +\alpha )t)+\cos \left((\omega -\alpha )t\right)&=\operatorname {Re} \left(e^{i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\&=\operatorname {Re} \left(\left(e^{i\alpha t}+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\&=\operatorname {Re} \left(2\cos(\alpha t)\cdot e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \operatorname {Re} \left(e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \cos \left(\omega t\right).\end{aligned}}}$$

En física

Electromagnetismo e ingeniería eléctrica

En ingeniería eléctrica , la transformada de Fourier se utiliza para analizar tensiones y corrientes variables . El tratamiento de resistencias , condensadores e inductores se puede unificar introduciendo resistencias imaginarias dependientes de la frecuencia para los dos últimos y combinando las tres en un único número complejo llamado impedancia . Este enfoque se denomina cálculo fasorial .

En ingeniería eléctrica, la unidad imaginaria se denota por j , para evitar confusiones con I , que generalmente se utiliza para denotar corriente eléctrica , o, más particularmente, i , que generalmente se utiliza para denotar corriente eléctrica instantánea.

Debido a que el voltaje en un circuito de CA es oscilante, se puede representar como

$${\displaystyle V(t)=V_{0}e^{j\omega t}=V_{0}\left(\cos \omega t+j\sin \omega t\right),}$$

Para obtener la cantidad medible se toma la parte real:

$${\displaystyle v(t)=\operatorname {Re} (V)=\operatorname {Re} \left[V_{0}e^{j\omega t}\right]=V_{0}\cos \omega t.}$$

La señal de valor complejo V ( t ) se denomina representación analítica de la señal medible de valor real v ( t ) . ^[53]

Dinámica de fluidos

En dinámica de fluidos , se utilizan funciones complejas para describir el flujo potencial en dos dimensiones .

Mecánica cuántica

El campo de números complejos es intrínseco a las formulaciones matemáticas de la mecánica cuántica , donde los espacios de Hilbert complejos proporcionan el contexto para una formulación de este tipo que es conveniente y quizás la más estándar. Las fórmulas originales de la mecánica cuántica –la ecuación de Schrödinger y la mecánica matricial de Heisenberg– hacen uso de números complejos.

Relatividad

En la relatividad especial y general , algunas fórmulas para la métrica del espacio-tiempo se vuelven más simples si se toma el componente temporal del continuo espacio-tiempo como imaginario. (Este enfoque ya no es estándar en la relatividad clásica, pero se utiliza de manera esencial en la teoría cuántica de campos ). Los números complejos son esenciales para los espinores , que son una generalización de los tensores utilizados en la relatividad.

Caracterizaciones, generalizaciones y nociones relacionadas

Caracterización algebraica

El campo tiene las siguientes tres propiedades: ${\displaystyle \mathbb {C} }$

• En primer lugar, tiene característica 0. Esto significa que 1 + 1 + ⋯ + 1 ≠ 0 para cualquier número de sumandos (todos iguales a uno).
• En segundo lugar, su grado de trascendencia sobre , el campo primo de es la cardinalidad del continuo . ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} ,}$
• En tercer lugar, es algebraicamente cerrado (ver arriba).

Se puede demostrar que cualquier cuerpo que tenga estas propiedades es isomorfo (como cuerpo) a Por ejemplo, la clausura algebraica del cuerpo del número p -ádico también satisface estas tres propiedades, por lo que estos dos cuerpos son isomorfos (como cuerpos, pero no como cuerpos topológicos). ^[54] Además, es isomorfo al cuerpo de la serie compleja de Puiseux . Sin embargo, especificar un isomorfismo requiere el axioma de elección . Otra consecuencia de esta caracterización algebraica es que contiene muchos subcuerpos propios que son isomorfos a . ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Caracterización como campo topológico

La caracterización precedente de describe únicamente los aspectos algebraicos de Es decir, no se tratan las propiedades de proximidad y continuidad , que son importantes en áreas como el análisis y la topología . La siguiente descripción de como un campo topológico (es decir, un campo que está equipado con una topología , que permite la noción de convergencia) sí tiene en cuenta las propiedades topológicas. contiene un subconjunto P (es decir, el conjunto de números reales positivos) de elementos distintos de cero que satisfacen las tres condiciones siguientes: ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

• P está cerrado bajo adición, multiplicación y toma de inversas.
• Si x e y son elementos distintos de P , entonces x − y o y − x está en P .
• Si S es cualquier subconjunto no vacío de P , entonces S + P = x + P para algún x en ${\displaystyle \mathbb {C} .}$

Además, tiene un automorfismo involutivo no trivial x ↦ x * (es decir, la conjugación compleja), tal que x x * está en P para cualquier x distinto de cero en ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$

Cualquier cuerpo F con estas propiedades puede ser dotado de una topología tomando los conjuntos B ( x ,  p ) = {  y | p − ( y − x )( y − x )* ∈ P  }  como base , donde x se extiende sobre el cuerpo y p se extiende sobre P. Con esta topología, F es isomorfo como cuerpo topológico a ${\displaystyle \mathbb {C} .}$

Los únicos campos topológicos localmente compactos conexos son y Esto da otra caracterización de como un campo topológico, porque se puede distinguir de porque los números complejos distintos de cero están conexos , mientras que los números reales distintos de cero no lo están. ^[55] ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} }$

Otros sistemas numéricos

El proceso de extender el cuerpo de números reales a es una instancia de la construcción de Cayley–Dickson . La aplicación iterativa de esta construcción a produce entonces los cuaterniones , los octoniones , ^[56] los sedeniones y los trigintaduoniones . Esta construcción resulta disminuir las propiedades estructurales de los sistemas numéricos involucrados. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

A diferencia de los reales, no es un cuerpo ordenado , es decir, no es posible definir una relación z ₁ < z ₂ que sea compatible con la adición y la multiplicación. De hecho, en cualquier cuerpo ordenado, el cuadrado de cualquier elemento es necesariamente positivo, por lo que i ² = −1 impide la existencia de una ordenación sobre ^[57] Pasando de a los cuaterniones pierde conmutatividad, mientras que los octoniones (además de no ser conmutativos) dejan de ser asociativos. Los reales, números complejos, cuaterniones y octoniones son todas álgebras de división normadas sobre . Por el teorema de Hurwitz son las únicas; los sedeniones , el siguiente paso en la construcción de Cayley-Dickson, no tienen esta estructura. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} }$

La construcción de Cayley-Dickson está estrechamente relacionada con la representación regular de pensamiento de como un álgebra - (un espacio vectorial - con una multiplicación), con respecto a la base (1,  i ) . Esto significa lo siguiente: la función -lineal para algún número complejo fijo w puede representarse mediante una matriz 2 × 2 (una vez que se ha elegido una base). Con respecto a la base (1,  i ) , esta matriz es es decir, la mencionada en la sección sobre representación matricial de números complejos anterior. Si bien esta es una representación lineal de en las matrices reales 2 × 2 , no es la única. Cualquier matriz tiene la propiedad de que su cuadrado es el negativo de la matriz identidad: J ² = − I . Entonces también es isomorfa al cuerpo y da una estructura compleja alternativa en Esto se generaliza mediante la noción de estructura compleja lineal . ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ $${\displaystyle {\begin{aligned}\mathbb {C} &\rightarrow \mathbb {C} \\z&\mapsto wz\end{aligned}}}$$ $${\displaystyle {\begin{pmatrix}\operatorname {Re} (w)&-\operatorname {Im} (w)\\\operatorname {Im} (w)&\operatorname {Re} (w)\end{pmatrix}},}$$ ${\displaystyle \mathbb {C} }$ $${\displaystyle J={\begin{pmatrix}p&q\\r&-p\end{pmatrix}},\quad p^{2}+qr+1=0}$$ $${\displaystyle \{z=aI+bJ:a,b\in \mathbb {R} \}}$$ ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {R} ^{2}.}$

Los números hipercomplejos también se generalizan y Por ejemplo, esta noción contiene los números complejos divididos , que son elementos del anillo (a diferencia de para los números complejos). En este anillo, la ecuación a ² = 1 tiene cuatro soluciones. ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} ,}$ ${\displaystyle \mathbb {O} .}$ ${\displaystyle \mathbb {R} [x]/(x^{2}-1)}$ ${\displaystyle \mathbb {R} [x]/(x^{2}+1)}$

El cuerpo es la completitud del cuerpo de números racionales , con respecto a la métrica de valor absoluto usual . Otras opciones de métricas en conducen a los cuerpos de números p -ádicos (para cualquier número primo p ), que son por lo tanto análogos a . No hay otras formas no triviales de completar que y por el teorema de Ostrowski . Los cierres algebraicos de todavía tienen una norma, pero (a diferencia de ) no son completos con respecto a ella. La completitud de resulta ser algebraicamente cerrada. Por analogía, el cuerpo se llama números complejos p -ádicos. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} ,}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} _{p},}$ ${\displaystyle {\overline {\mathbb {Q} _{p}}}}$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} _{p}}$ ${\displaystyle {\overline {\mathbb {Q} _{p}}}}$

Los campos y sus extensiones de campo finitas, incluidos los campos locales, se denominan campos locales . ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {Q} _{p},}$ ${\displaystyle \mathbb {C} ,}$

Véase también

• Continuación analítica
• Movimiento circular utilizando números complejos
• Sistema de base compleja
• Espacio de coordenadas complejo
• Geometría compleja
• Geometría de los números
• Número complejo dual
• Número entero de Eisenstein
• Álgebra geométrica (que incluye el plano complejo como subespacio espinorial bidimensional ) ${\displaystyle {\mathcal {G}}_{2}^{+}}$
• Número complejo unitario

Notas

1. Solomentsev 2001: "El plano cuyos puntos se identifican con los elementos de se llama plano complejo... La interpretación geométrica completa de los números complejos y las operaciones con ellos aparecieron por primera vez en el trabajo de C. Wessel (1799). La representación geométrica de los números complejos, a veces llamada "diagrama de Argand", comenzó a usarse después de la publicación en 1806 y 1814 de los artículos de JR Argand, quien redescubrió, en gran parte de forma independiente, los hallazgos de Wessel". ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {C} }$
2. En la literatura la unidad imaginaria a menudo precede al signo radical, incluso cuando éste está precedido por un número entero. ^[23]
3. Pierre Laurent Wantzel en 1843, Vincenzo Mollame en 1890, Otto Hölder en 1891 y Adolf Kneser en 1892 demostraron que los números imaginarios aparecen necesariamente en la fórmula cúbica cuando la ecuación tiene tres raíces reales diferentes. Paolo Ruffini también proporcionó una prueba incompleta en 1799. ——S. Confalonieri (2015) ^[25]
4. Argand 1814, pag. 204 define el módulo de un número complejo pero no lo nombra:
   "Dans ce qui suit, les accens, indifféremment placecés, seront usedés pour indicar la grandeur absolue des quantités qu'ils afectont; ainsi, si , et étant réels, on devra entender que ou ." ${\displaystyle a=m+n{\sqrt {-1}}}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle a_{'}}$ ${\displaystyle a'={\sqrt {m^{2}+n^{2}}}}$
   [En lo que sigue, los acentos, dondequiera que se coloquen, se utilizarán para indicar el tamaño absoluto de las cantidades a las que están asignados; así si , y siendo real, se debe entender que o .] Argand 1814, p. 208 define y nombra el módulo y el factor de dirección de un número complejo: "...  pourrait être appelé le module de , et représenterait la grandeur absolue de la ligne , tandis que l'autre facteur, dont le module est l'unité, en représenterait la dirección." [...  podría llamarse el módulo de y representaría el tamaño absoluto de la línea (Argand representó números complejos como vectores), mientras que el otro factor [es decir, ], cuyo módulo es la unidad [1], representaría su dirección. ] ${\displaystyle a=m+n{\sqrt {-1}}}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle a_{'}}$ ${\displaystyle a'={\sqrt {m^{2}+n^{2}}}}$
   ${\displaystyle a={\sqrt {m^{2}+n^{2}}}}$ ${\displaystyle a+b{\sqrt {-1}}}$ ${\displaystyle a+b{\sqrt {-1}}}$
   ${\displaystyle a={\sqrt {m^{2}+n^{2}}}}$ ${\displaystyle a+b{\sqrt {-1}}}$ ${\displaystyle a+b{\sqrt {-1}}\,,}$ ${\displaystyle {\tfrac {a}{\sqrt {a^{2}+b^{2}}}}+{\tfrac {b}{\sqrt {a^{2}+b^{2}}}}{\sqrt {-1}}}$
5. Gauss escribe: ^[45] "Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates imaginarias extenditur, ita ut absque restricte ipsius obiectum constituant numeri formae a + bi , denotantibus i , pro more quantitatem imaginariam , atque ${\displaystyle {\sqrt {-1}}}$ a, b indefinite omnes numeros reales integros inter - et + . ${\displaystyle \infty }$ ${\displaystyle \infty }$ [Por supuesto, así como la aritmética superior ha sido investigada hasta ahora sólo en problemas entre números enteros reales, así también los teoremas sobre residuos bicuadráticos brillan en su mayor simplicidad y genuina belleza, cuando el campo de la aritmética se extiende a cantidades imaginarias , de modo que, sin restricciones al respecto, los números de la forma a + bi — i denotan por convención la cantidad imaginaria , y las variables a, b [denotan] todos los números enteros reales entre y — constituyen un objeto.] ${\displaystyle {\sqrt {-1}}}$ ${\displaystyle -\infty }$ ${\displaystyle +\infty }$
6. Gauss: ^[46] "Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur." [Llamamos a estos números [es decir, números de la forma a + bi ] "números enteros complejos", de modo que los [números] reales se consideran no como el opuesto de los [números] complejos sino [como] un tipo [de número que] está, por así decirlo, contenido dentro de ellos.]
7. Gauss: ^[47] "Productum numeri complexi per numerum ipsi conjunctum utriusque normam vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est". [Llamamos "norma" al producto de un número complejo [por ejemplo, a + ib ] por su conjugado [ a - ib ]. Por tanto, el cuadrado de un número real debe considerarse como su norma.]
8. Sin embargo, para otra función inversa de la función exponencial compleja (y no el valor principal definido anteriormente), el corte de la rama podría tomarse en cualquier otro rayo que pase por el origen.

Referencias

1. Para una descripción detallada de la historia de los números "imaginarios", desde el escepticismo inicial hasta la aceptación final, véase Bourbaki, Nicolas (1998). "Fundamentos de las matemáticas § Lógica: teoría de conjuntos". Elementos de la historia de las matemáticas . Springer. pp. 18–24.
2. "Los números complejos, tanto como los reales, y quizás incluso más, encuentran una unidad con la naturaleza que es verdaderamente notable. Es como si la Naturaleza misma estuviera tan impresionada por el alcance y la consistencia del sistema de números complejos como nosotros mismos, y hubiera confiado a estos números las operaciones precisas de su mundo en sus escalas más minúsculas.", Penrose 2005, pp.72-73.
3. Axler, Sheldon (2010). Álgebra universitaria . Wiley. pág. 262. ISBN 9780470470770.
4. Spiegel, señor; Lipschutz, S.; Schiller, JJ; Spellman, D. (14 de abril de 2009). Variables complejas . Serie de esquemas de Schaum (2ª ed.). McGraw-Hill. ISBN 978-0-07-161569-3.
5. Aufmann, Barker & Nation 2007, pág. 66, Capítulo P
6. Pedoe, Dan (1988). Geometría: un curso completo . Dover. ISBN 978-0-486-65812-4.
7. Weisstein, Eric W. "Número complejo". mathworld.wolfram.com . Consultado el 12 de agosto de 2020 .
8. Campbell, George Ashley (abril de 1911). "Oscilaciones cisoidales" (PDF) . Actas del Instituto Americano de Ingenieros Eléctricos . XXX (1–6). Instituto Americano de Ingenieros Eléctricos : 789–824 [Fig. 13 en la pág. 810]. doi :10.1109/PAIEE.1911.6659711. S2CID  51647814 . Consultado el 24 de junio de 2023 . p. 789: El uso de i (o ı griega ) para el símbolo imaginario es casi universal en el trabajo matemático, lo que es una razón muy sólida para conservarlo en las aplicaciones de las matemáticas en la ingeniería eléctrica. Sin embargo, además de la cuestión de las convenciones establecidas y la facilidad de referencia a la literatura matemática, la sustitución del símbolo j es objetable debido a la terminología vectorial con la que se ha asociado en la literatura de ingeniería, y también debido a la confusión resultante de la práctica dividida de los escritores de ingeniería, algunos usando j para + i y otros usando j para − i .
9. Brown, James Ward; Churchill, Ruel V. (1996). Variables complejas y aplicaciones (6.ª ed.). Nueva York, EE. UU.: McGraw-Hill . p. 2. ISBN. 978-0-07-912147-9. p. 2: En ingeniería eléctrica, se utiliza la letra j en lugar de i .
10. Apóstol 1981, págs. 15-16.
11. Apostol 1981, págs. 15-16
12. Apóstol 1981, pág. 18.
13. Otros autores, incluido Ebbinghaus et al. 1991, §6.1, eligieron que el argumento estuviera en el intervalo . ${\displaystyle [0,2\pi )}$
14. Kasana, HS (2005). "Capítulo 1". Variables complejas: teoría y aplicaciones (2.ª ed.). PHI Learning Pvt. Ltd., pág. 14. ISBN 978-81-203-2641-5.
15. Nilsson, James William; Riedel, Susan A. (2008). "Capítulo 9". Circuitos eléctricos (8.ª ed.). Prentice Hall. pág. 338. ISBN 978-0-13-198925-2.
16. Bourbaki 1998, §VIII.1
17. Kline, Morris. Una historia del pensamiento matemático, volumen 1 , pág. 253.
18. Jurij., Kovič. Tristan Needham, Visual Complex Analysis, Oxford University Press Inc., Nueva York, 1998, 592 páginas. OCLC  1080410598.
19. O'Connor y Robertson (2016), "Girolamo Cardano".
20. Nahin, Paul J. Un cuento imaginario: La historia de √−1. Princeton: Princeton University Press, 1998.
21. Katz, Victor J. (2004). "9.1.4". Una historia de las matemáticas, versión breve . Addison-Wesley . ISBN 978-0-321-16193-2.
22. Hamilton, Wm. (1844). "Sobre una nueva especie de cantidades imaginarias relacionadas con una teoría de cuaterniones". Actas de la Real Academia Irlandesa . 2 : 424–434.
23. Cynthia Y. Young (2017). Trigonometría (4.ª ed.). John Wiley & Sons. pág. 406. ISBN 978-1-119-44520-3.Extracto de la página 406
24. Nahin, Paul J. (2007). Un cuento imaginario: la historia de √−1. Prensa de la Universidad de Princeton . ISBN 978-0-691-12798-9Archivado desde el original el 12 de octubre de 2012 . Consultado el 20 de abril de 2011 .
25. Confalonieri, Sara (2015). El intento inalcanzable de evitar el casus irreducibilis de las ecuaciones cúbicas: De Regula Aliza de Gerolamo Cardano . Saltador. Págs. 15 y 16 (nota 26). ISBN 978-3658092757.
26. Descartes, René (1954) [1637]. La geometría | La Geometría de René Descartes con un facsímil de la primera edición. Publicaciones de Dover . ISBN 978-0-486-60068-0. Recuperado el 20 de abril de 2011 .
27. Euler, Leonard (1748). Introductio in Analysin Infinitorum [ Introducción al análisis del infinito ] (en latín). Vol. 1. Lucerna, Suiza: Marc Michel Bosquet & Co. p. 104.
28. Wessel, Caspar (1799). "Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning" [Sobre la representación analítica de la dirección, esfuerzo aplicado en particular a la determinación de polígonos planos y esféricos]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [Nueva colección de escritos de la Real Sociedad Científica Danesa] (en danés). 5 : 469–518.
29. Wallis, John (1685). Tratado de álgebra, tanto histórica como práctica... Londres, Inglaterra: impreso por John Playford, para Richard Davis. págs. 264–273.
30. Argand (1806). Essai sur une manière de représenter les quantités imaginaires dans les constructs géométriques [ Ensayo sobre una forma de representar cantidades complejas mediante construcciones geométricas ] (en francés). París, Francia: Madame Veuve Blanc.
31. Gauss, Carl Friedrich (1799) "Demonstratio nova theorematis omnem functionem algebraicam racionalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse". [Nueva prueba del teorema de que cualquier función algebraica integral racional de una sola variable puede resolverse en factores reales de primer o segundo grado.] Ph.D. Tesis, Universidad de Helmstedt, (Alemania). (en latín)
32. Ewald, William B. (1996). De Kant a Hilbert: un libro de consulta sobre los fundamentos de las matemáticas. Vol. 1. Oxford University Press. pág. 313. ISBN 9780198505358. Recuperado el 18 de marzo de 2020 .
33. Gauss 1831.
34. "Adrien Quentin Buée (1745-1845): MacTutor".
35. Buée (1806). "Mémoire sur les quantités imaginaires" [Memoria sobre cantidades imaginarias]. Transacciones filosóficas de la Royal Society de Londres (en francés). 96 : 23–88. doi :10.1098/rstl.1806.0003. S2CID  110394048.
36. Mourey, CV (1861). La vraies théore des quantités négatives et des quantités prétendues imaginaires [ La verdadera teoría de las cantidades negativas y de las supuestas cantidades imaginarias ] (en francés). París, Francia: Mallet-Bachelier. Reimpresión de 1861 del original de 1828.
37. Warren, John (1828). Tratado sobre la representación geométrica de las raíces cuadradas de cantidades negativas. Cambridge, Inglaterra: Cambridge University Press.
38. Warren, John (1829). "Consideración de las objeciones planteadas contra la representación geométrica de las raíces cuadradas de cantidades negativas". Philosophical Transactions of the Royal Society of London . 119 : 241–254. doi : 10.1098/rstl.1829.0022 . S2CID  186211638.
39. Warren, John (1829). "Sobre la representación geométrica de las potencias de cantidades cuyos índices implican las raíces cuadradas de números negativos". Philosophical Transactions of the Royal Society of London . 119 : 339–359. doi : 10.1098/rstl.1829.0031 . S2CID  125699726.
40. Francés, JF (1813). "Nouveaux principes de géométrie de position, et interprétation géométrique des symboles imaginaires" [Nuevos principios de la geometría de posición e interpretación geométrica de símbolos [números] complejos]. Annales des mathématiques pures et appliquées (en francés). 4 : 61–71.
41. Caparrini, Sandro (2000). "Sobre el origen común de algunos de los trabajos sobre la interpretación geométrica de los números complejos". En Kim Williams (ed.). Two Cultures. Birkhäuser. pág. 139. ISBN 978-3-7643-7186-9.
42. Hardy, GH; Wright, EM (2000) [1938]. Introducción a la teoría de números . OUP Oxford . pág. 189 (cuarta edición). ISBN 978-0-19-921986-5.
43. Jeff Miller (21 de septiembre de 1999). "MÓDULO". Usos más antiguos conocidos de algunas palabras de las matemáticas (M) . Archivado desde el original el 3 de octubre de 1999.{{cite web}}: CS1 maint: unfit URL (link)
44. Cauchy, Augustin-Louis (1821). Cours d'analyse de l'École royale polytechnique (en francés). vol. 1. París, Francia: L'Imprimerie Royale. pag. 183.
45. Gauss 1831, pág. 96
46. Gauss 1831, pág. 96
47. Gauss 1831, pág. 98
48. Hankel, Hermann (1867). Vorlesungen über die complexen Zahlen und ihre Functionen [ Conferencias sobre los números complejos y sus funciones ] (en alemán). vol. 1. Leipzig, [Alemania]: Leopold Voss. pag. 71. De la pág. 71: "Wir werden den Factor ( cos φ + i sin φ) haüfig den Richtungscoficienten nennen". (A menudo llamaremos al factor (cos φ + i sen φ) el "coeficiente de dirección".)
49. Bourbaki 1998, §VIII.1
50. Lester, JA (1994). "Triángulos I: Formas". Aecuaciones Mathematicae . 52 : 30–54. doi :10.1007/BF01818325. S2CID  121095307.
51. Kalman, Dan (2008a). "Una prueba elemental del teorema de Marden". American Mathematical Monthly . 115 (4): 330–38. doi :10.1080/00029890.2008.11920532. ISSN  0002-9890. S2CID  13222698. Archivado desde el original el 8 de marzo de 2012 . Consultado el 1 de enero de 2012 .
52. Kalman, Dan (2008b). «El teorema más maravilloso de las matemáticas». Journal of Online Mathematics and Its Applications . Archivado desde el original el 8 de febrero de 2012. Consultado el 1 de enero de 2012 .
53. Grant, IS; Phillips, WR (2008). Electromagnetismo (2.ª ed.). Manchester Physics Series. ISBN 978-0-471-92712-9.
54. Marker, David (1996). "Introducción a la teoría de modelos de campos". En Marker, D.; Messmer, M.; Pillay, A. (eds.). Teoría de modelos de campos . Notas de clase en lógica. Vol. 5. Berlín: Springer-Verlag. págs. 1–37. ISBN 978-3-540-60741-0.Señor 1477154  .
55. Bourbaki 1998, §VIII.4.
56. McCrimmon, Kevin (2004). Una muestra de las álgebras de Jordan . Universitext. Springer. pág. 64. ISBN 0-387-95447-3. Sr. 2014924
57. Apóstol 1981, pág. 25.

• Ahlfors, Lars (1979). Análisis complejo (3.ª ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
• Andreescu, Titu; Andrica, Dorin (2014), Números complejos de la A a la Z (Segunda ed.), Nueva York: Springer, doi :10.1007/978-0-8176-8415-0, ISBN 978-0-8176-8414-3
• Apostol, Tom (1981). Análisis matemático . Addison-Wesley.
• Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007). Álgebra universitaria y trigonometría (6.ª ed.). Cengage Learning. ISBN 978-0-618-82515-8.
• Conway, John B. (1986). Funciones de una variable compleja I. Springer. ISBN 978-0-387-90328-6.
• Derbyshire, John (2006). Cantidad desconocida: Una historia real e imaginaria del álgebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
• Joshi, Kapil D. (1989). Fundamentos de las matemáticas discretas . Nueva York: John Wiley & Sons . ISBN. 978-0-470-21152-6.
• Needham, Tristan (1997). Análisis visual complejo . Clarendon Press. ISBN 978-0-19-853447-1.
• Pedoe, Dan (1988). Geometría: un curso completo . Dover. ISBN 978-0-486-65812-4.
• Penrose, Roger (2005). El camino a la realidad: una guía completa sobre las leyes del universo. Alfred A. Knopf. ISBN 978-0-679-45443-4.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Sección 5.5 Aritmética compleja". Recetas numéricas: el arte de la computación científica (3.ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-88068-8Archivado desde el original el 13 de marzo de 2020 . Consultado el 9 de agosto de 2011 .
• Solomentsev, ED (2001) [1994], "Número complejo", Enciclopedia de Matemáticas , EMS Press

Referencias históricas

• Argán (1814). "Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la demostration d'un theorème d'analise" [Reflexiones sobre la nueva teoría de los números complejos, seguidas de una aplicación a la demostración de un teorema de análisis]. Annales de mathématiques pures et appliquées (en francés). 5 : 197–209.
• Bourbaki, Nicolas (1998). "Fundamentos de las matemáticas § lógica: teoría de conjuntos". Elementos de la historia de las matemáticas . Springer.
• Burton, David M. (1995). Historia de las matemáticas (3.ª ed.). Nueva York: McGraw-Hill . ISBN 978-0-07-009465-9.
• Gauss, CF (1831). "Theoria residuorum biquadraticorum. Commentatio secunda" [Teoría de los residuos bicuadráticos. Segunda memoria.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (en latín). 7 : 89-148.
• Katz, Victor J. (2004). Una historia de las matemáticas, versión breve . Addison-Wesley . ISBN 978-0-321-16193-2.
• Nahin, Paul J. (1998). Un cuento imaginario: la historia de ${\displaystyle \scriptstyle {\sqrt {-1}}}$ . Prensa de la Universidad de Princeton. ISBN 978-0-691-02795-1.—Una introducción suave a la historia de los números complejos y los comienzos del análisis complejo.
• Ebbinghaus, HD; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). Números (edición de tapa dura). Saltador. ISBN 978-0-387-97497-2.— Una perspectiva avanzada sobre el desarrollo histórico del concepto de número.