En matemáticas , especialmente en matemáticas históricas y recreativas , una matriz cuadrada de números, generalmente enteros positivos , se denomina cuadrado mágico si las sumas de los números en cada fila, cada columna y ambas diagonales principales son iguales. [1] [2] El "orden" del cuadrado mágico es el número de números enteros a lo largo de un lado ( n ), y la suma constante se llama " constante mágica ". Si la matriz incluye solo los números enteros positivos , se dice que el cuadrado mágico es "normal". Algunos autores interpretan "cuadrado mágico" como "cuadrado mágico normal". [3]
Los cuadrados mágicos que incluyen entradas repetidas no entran en esta definición y se denominan "triviales". Algunos ejemplos conocidos, como el cuadrado mágico de la Sagrada Familia y el cuadrado de Parker, son triviales en este sentido. Cuando todas las filas y columnas, pero no ambas diagonales, suman la constante mágica, se obtiene un cuadrado semimágico (a veces llamado cuadrado ortomágico ).
El estudio matemático de un cuadrado mágico generalmente se ocupa de su construcción, clasificación y enumeración. Aunque no existen métodos completamente generales para producir todos los cuadrados mágicos de todos los órdenes, históricamente se han descubierto tres técnicas generales: por el método de borde, haciendo cuadrados mágicos compuestos y añadiendo dos cuadrados preliminares. También hay estrategias más específicas como el método de enumeración continua que reproduce patrones específicos. Los cuadrados mágicos generalmente se clasifican según su orden n como: impar si n es impar, uniformemente par (también conocido como "doblemente par") si n es un múltiplo de 4, imparmente par (también conocido como "simplemente par") si n es cualquier otro número par. Esta clasificación se basa en diferentes técnicas necesarias para construir cuadrados impares, uniformemente pares e imparmente pares. Además de esto, dependiendo de otras propiedades, los cuadrados mágicos también se clasifican como cuadrados mágicos asociativos , cuadrados mágicos pandiagonales , cuadrados mágicos más perfectos , etc. Más desafiante aún es el intento de clasificar todos los cuadrados mágicos de un orden determinado como transformaciones de un conjunto más pequeño de cuadrados. A excepción de n ≤ 5, la enumeración de cuadrados mágicos de orden superior sigue siendo un desafío abierto. La enumeración de los cuadrados mágicos más perfectos de cualquier orden recién se logró a fines del siglo XX.
Los cuadrados mágicos tienen una larga historia, que se remonta al menos al año 190 a. C. en China. En diversas épocas han adquirido un significado oculto o mítico y han aparecido como símbolos en obras de arte. En la época moderna se han generalizado de diversas maneras, entre ellas, mediante el uso de restricciones adicionales o diferentes, la multiplicación en lugar de la adición de celdas, el uso de formas alternativas o más de dos dimensiones y la sustitución de números por formas y la adición por operaciones geométricas.

.jpg/440px-Albrecht_Dürer_-_Melencolia_I_(detail).jpg)

El cuadrado mágico de tercer orden era conocido por los matemáticos chinos ya en el año 190 a. C., y fue dado explícitamente en el primer siglo de la era común. El primer ejemplo datable del cuadrado mágico de cuarto orden ocurrió en el año 587 d. C. en la India. Ejemplos de cuadrados mágicos de orden 3 a 9 aparecen en una enciclopedia de Bagdad de alrededor del año 983 , la Enciclopedia de los Hermanos de la Pureza ( Rasa'il Ikhwan al-Safa ). A finales del siglo XII, los métodos generales para construir cuadrados mágicos estaban bien establecidos. En esa época, algunos de estos cuadrados se usaban cada vez más junto con letras mágicas, como en Shams Al-ma'arif , para fines ocultistas. [4] En la India, Narayana enumeró todos los cuadrados mágicos pandiagonales de cuarto orden en 1356. Los cuadrados mágicos se dieron a conocer en Europa a través de la traducción de fuentes árabes como objetos ocultos durante el Renacimiento, y la teoría general tuvo que redescubrirse independientemente de los desarrollos previos en China, India y Oriente Medio. También son notables las culturas antiguas con una tradición de matemáticas y numerología que no descubrieron los cuadrados mágicos: griegos, babilonios, egipcios y americanos precolombinos.

Aunque las referencias antiguas al patrón de números pares e impares en el cuadrado mágico 3×3 aparecen en el I Ching , la primera instancia inequívoca de este cuadrado mágico aparece en el capítulo llamado Mingtang (Salón Brillante) de un libro del siglo I Da Dai Liji (Registro de Ritos del Anciano Dai), que pretendía describir los antiguos ritos chinos de la dinastía Zhou. [5] [6] [7] [8] Estos números también aparecen en un texto matemático posiblemente anterior llamado Shushu jiyi (Memorias sobre algunas tradiciones del arte matemático), que se dice que fue escrito en 190 a. C. Esta es la primera aparición registrada de un cuadrado mágico; y se utilizó principalmente para adivinación y astrología. [5] El cuadrado mágico 3×3 fue denominado los "Nueve Salones" por los primeros matemáticos chinos. [7] La identificación del cuadrado mágico 3×3 con el legendario diagrama de Luoshu se hizo recién en el siglo XII, después de lo cual se lo denominó cuadrado de Luoshu. [5] [7] El tratado chino más antiguo que se conserva que muestra cuadrados mágicos de orden mayor que 3 es Xugu zheqi suanfa (Continuación de los métodos matemáticos antiguos para dilucidar lo extraño) de Yang Hui escrito en 1275. [5] [7] El contenido del tratado de Yang Hui se recopiló de obras más antiguas, tanto nativas como extranjeras; y solo explica la construcción de cuadrados mágicos de tercer y cuarto orden, mientras que simplemente transmite los diagramas terminados de cuadrados más grandes. [7] Da un cuadrado mágico de orden 3, dos cuadrados para cada orden de 4 a 8, uno de orden nueve y un cuadrado semimágico de orden 10. También da seis círculos mágicos de diversa complejidad. [9]
Los cuadrados mágicos de orden 3 a 9 anteriores están tomados del tratado de Yang Hui, en el que el principio de Luo Shu es claramente evidente. [7] [8] El cuadrado de orden 5 es un cuadrado mágico bordeado, con un cuadrado central de 3 × 3 formado según el principio de Luo Shu. El cuadrado de orden 9 es un cuadrado mágico compuesto, en el que los nueve subcuadrados de 3 × 3 también son mágicos. [7] Después de Yang Hui, los cuadrados mágicos aparecen con frecuencia en las matemáticas chinas, como en el Dayan suoyin de Ding Yidong ( c. 1300 ), el Suanfa tongzong de Cheng Dawei (1593), el Shuduyan de Fang Zhongtong (1661) que contiene círculos, cubos y esferas mágicos, el Xinzhai zazu de Zhang Chao ( c. 1650 ), que publicó el primer cuadrado mágico de China de orden diez, y por último el Binaishanfang ji de Bao Qishou ( c. 1880 ), que dio varias configuraciones mágicas tridimensionales. [5] [8] Sin embargo, a pesar de ser el primero en descubrir los cuadrados mágicos y obtener una ventaja de varios siglos, el desarrollo chino de los cuadrados mágicos es muy inferior en comparación con los desarrollos indios, de Oriente Medio o europeos. El punto culminante de las matemáticas chinas que tratan los cuadrados mágicos parece estar contenido en el trabajo de Yang Hui; pero incluso como una colección de métodos más antiguos, este trabajo es mucho más primitivo, carente de métodos generales para construir cuadrados mágicos de cualquier orden, en comparación con una colección similar escrita en la misma época por el erudito bizantino Manuel Moschopoulos . [7] Esto posiblemente se deba a la fascinación de los eruditos chinos por el principio de Lo Shu, que intentaron adaptar para resolver cuadrados superiores; y después de Yang Hui y la caída de la dinastía Yuan , su purga sistemática de las influencias extranjeras en las matemáticas chinas. [7]
Japón y China tienen tradiciones matemáticas similares y se han influenciado mutuamente en repetidas ocasiones en la historia de los cuadrados mágicos. [10] El interés japonés en los cuadrados mágicos comenzó después de la difusión de obras chinas ( Suanfa de Yang Hui y Suanfa tongzong de Cheng Dawei ) en el siglo XVII y, como resultado, casi todos los wasans dedicaron su tiempo a su estudio.
En la edición de 1660 de Ketsugi-sho , Isomura Kittoku dio cuadrados mágicos con borde tanto pares como impares, así como círculos mágicos; mientras que la edición de 1684 del mismo libro contenía una gran sección sobre cuadrados mágicos, demostrando que tenía un método general para construir cuadrados mágicos con borde. [11] En Jinko-ki (1665) de Muramatsu Kudayu Mosei, se muestran tanto cuadrados mágicos como círculos mágicos. El cuadrado más grande que construye Mosei es de orden 19. Varios cuadrados mágicos y círculos mágicos también fueron publicados por Nozawa Teicho en Dokai-sho (1666), Sato Seiko en Kongenki (1666) y Hosino Sanenobu en Ko-ko-gen Sho (1673). [12] Uno de los Siete Libros de Seki Takakazu ( Hojin Yensan ) (1683) está dedicado completamente a los cuadrados y círculos mágicos. Este es el primer libro japonés que da un tratamiento general de los cuadrados mágicos en el que se describen claramente los algoritmos para construir cuadrados mágicos con bordes impares, simplemente pares y doblemente pares. [13] En 1694 y 1695, Yueki Ando dio diferentes métodos para crear los cuadrados mágicos y mostró cuadrados de orden 3 a 30. Un cubo mágico de cuarto orden fue construido por Yoshizane Tanaka (1651-1719) en Rakusho-kikan (1683). El estudio de los cuadrados mágicos fue continuado por los alumnos de Seki, en particular por Katahiro Takebe, cuyos cuadrados fueron mostrados en el cuarto volumen de Ichigen Kappo por Shukei Irie, Yoshisuke Matsunaga en Hojin-Shin-jutsu , Yoshihiro Kurushima en Kyushi Iko quien redescubrió un método para producir los cuadrados impares dado por Agrippa, [14] y Naonobu Ajima . [15] [16] Así, a principios del siglo XVIII, los matemáticos japoneses poseían métodos para construir cuadrados mágicos de orden arbitrario. Después de esto, los intentos de enumerar los cuadrados mágicos fueron iniciados por Nushizumi Yamaji. [16]

El cuadrado mágico 3×3 aparece por primera vez en la India en Gargasamhita de Garga, quien recomienda su uso para pacificar los nueve planetas ( navagraha ). La versión más antigua de este texto data del año 100 d. C., pero el pasaje sobre los planetas no podría haber sido escrito antes del año 400 d. C. El primer ejemplo datable del cuadrado mágico 3×3 en la India aparece en un texto médico Siddhayog ( c. 900 d. C. ) de Vrnda, que se prescribía a las mujeres en labor de parto para facilitar el parto. [17]
El cuadrado mágico de cuarto orden más antiguo del mundo se encuentra en una obra enciclopédica escrita por Varahamihira alrededor del año 587 d. C. llamada Brhat Samhita . El cuadrado mágico se construyó con el propósito de hacer perfumes utilizando 4 sustancias seleccionadas de 16 sustancias diferentes. Cada celda del cuadrado representa un ingrediente particular, mientras que el número en la celda representa la proporción del ingrediente asociado, de modo que la mezcla de cualquier combinación de cuatro ingredientes a lo largo de las columnas, filas, diagonales, etc., da como resultado un volumen total de la mezcla de 18. Aunque el libro trata principalmente sobre adivinación, el cuadrado mágico se presenta como una cuestión de diseño combinatorio y no se le atribuyen propiedades mágicas. Las características especiales de este cuadrado mágico fueron comentadas por Bhattotpala ( c. 966 d. C. ) [18] [17]
El cuadrado de Varahamihira que se muestra arriba tiene una suma de 18. Aquí los números del 1 al 8 aparecen dos veces en el cuadrado. Es un cuadrado mágico pandiagonal . Se pueden obtener cuatro cuadrados mágicos diferentes sumando 8 a uno de los dos conjuntos de secuencias del 1 al 8. La secuencia se selecciona de manera que el número 8 se sume exactamente dos veces en cada fila, cada columna y cada una de las diagonales principales. Uno de los posibles cuadrados mágicos se muestra en el lado derecho. Este cuadrado mágico es notable porque es una rotación de 90 grados de un cuadrado mágico que aparece en el mundo islámico del siglo XIII como uno de los cuadrados mágicos más populares. [19]
La construcción del cuadrado mágico de cuarto orden se detalla en una obra titulada Kaksaputa , compuesta por el alquimista Nagarjuna alrededor del siglo X d. C. Todos los cuadrados dados por Nagarjuna son cuadrados mágicos de 4 × 4, y uno de ellos se llama Nagarjuniya en su honor. Nagarjuna dio un método para construir un cuadrado mágico de 4 × 4 utilizando un cuadrado esqueleto primario, dada una suma mágica par o impar. [18] El cuadrado de Nagarjuniya se da a continuación y tiene una suma total de 100.
El cuadrado de Nagarjuniya es un cuadrado mágico pandiagonal . El cuadrado de Nagarjuniya está formado por dos progresiones aritméticas que comienzan en 6 y 16 con ocho términos cada una, con una diferencia común entre términos sucesivos de 4. Cuando estas dos progresiones se reducen a la progresión normal de 1 a 8, se obtiene el cuadrado adyacente.
Alrededor del siglo XII, se inscribió un cuadrado mágico de 4×4 en la pared del templo de Parshvanath en Khajuraho , India. Varios himnos jainistas enseñan cómo hacer cuadrados mágicos, aunque no se puede datarlos. [17]
Hasta donde se sabe, el primer estudio sistemático de los cuadrados mágicos en la India fue realizado por Thakkar Pheru , un erudito jainista, en su Ganitasara Kaumudi (c. 1315). Esta obra contiene una pequeña sección sobre los cuadrados mágicos que consta de nueve versos. Aquí da un cuadrado de orden cuatro y alude a su reordenamiento; clasifica los cuadrados mágicos en tres (impar, par-par e impar-par) según su orden; da un cuadrado de orden seis; y prescribe un método para construir cada uno de los cuadrados pares e impares. Para los cuadrados pares, Pheru divide el cuadrado en cuadrados componentes de orden cuatro y coloca los números en celdas de acuerdo con el patrón de un cuadrado estándar de orden cuatro. Para los cuadrados impares, Pheru da el método utilizando el movimiento del caballo o movimiento del caballo . Aunque algorítmicamente diferente, da el mismo cuadrado que el método de De la Loubere. [17]
El siguiente trabajo exhaustivo sobre los cuadrados mágicos fue realizado por Narayana Pandit , quien en el capítulo catorce de su Ganita Kaumudi (1356) da métodos generales para su construcción, junto con los principios que gobiernan tales construcciones. Consta de 55 versos para las reglas y 17 versos para los ejemplos. Narayana da un método para construir todos los cuadrados panmágicos de cuarto orden utilizando el movimiento del caballo; enumera el número de cuadrados mágicos pandiagonales de orden cuatro, 384, incluyendo cada variación hecha por rotación y reflexión; tres métodos generales para cuadrados que tienen cualquier orden y suma constante cuando se conoce un cuadrado estándar del mismo orden; dos métodos para construir cuadrados par-par, par-impar y de cuadrados cuando se da la suma. Si bien Narayana describe un método más antiguo para cada especie de cuadrado, afirma que el método de superposición para cuadrados par-par e impar y un método de intercambio para cuadrados par-impar son de su propia invención. El método de superposición fue redescubierto más tarde por De la Hire en Europa. En la última sección, concibe otras figuras, como círculos, rectángulos y hexágonos, en las que los números pueden organizarse para poseer propiedades similares a las de los cuadrados mágicos. [18] [17] A continuación se presentan algunos de los cuadrados mágicos construidos por Narayana: [18]
El cuadrado de orden 8 es interesante en sí mismo, ya que es un ejemplo del cuadrado mágico más perfecto. Por cierto, Narayana afirma que el propósito de estudiar los cuadrados mágicos es construir yantra , destruir el ego de los malos matemáticos y para el placer de los buenos matemáticos. El tema de los cuadrados mágicos se conoce como bhadraganita y Narayana afirma que el dios Shiva fue el primero en enseñarlo a los hombres . [17]

Aunque no se conoce la historia temprana de los cuadrados mágicos en Persia y Arabia, se ha sugerido que eran conocidos en tiempos preislámicos. [20] Sin embargo, está claro que el estudio de los cuadrados mágicos era común en el Islam medieval , y se cree que comenzó después de la introducción del ajedrez en la región. [21] [22] [23] La primera aparición datable de un cuadrado mágico de orden 3 ocurre en el Kitab al-mawazin al-Saghir (El pequeño libro de las balanzas) de Jābir ibn Hayyān (fl. c. 721 - c. 815) , donde el cuadrado mágico y su numerología relacionada se asocian con la alquimia. [8] Si bien se sabe que los tratados sobre cuadrados mágicos se escribieron en el siglo IX, los primeros tratados existentes datan del siglo X: uno de Abu'l-Wafa al-Buzjani ( c. 998 ) y otro de Ali b. Ahmad al-Antaki ( c. 987 ). [22] [24] [25] Estos primeros tratados eran puramente matemáticos, y la designación árabe para los cuadrados mágicos utilizados es wafq al-a'dad , que se traduce como disposición armoniosa de los números . [23] A finales del siglo X, los dos tratados de Buzjani y Antaki dejan claro que los matemáticos de Oriente Medio habían entendido cómo construir cuadrados con borde de cualquier orden, así como cuadrados mágicos simples de órdenes pequeños ( n ≤ 6) que se utilizaban para hacer cuadrados mágicos compuestos. [22] [24] Un ejemplar de cuadrados mágicos de órdenes 3 a 9 ideados por matemáticos de Oriente Medio aparece en una enciclopedia de Bagdad de c. 983 , la Rasa'il Ikhwan al-Safa (la Enciclopedia de los Hermanos de la Pureza ). [26] Los cuadrados de orden 3 a 7 de Rasa'il se dan a continuación: [26]
En el siglo XI se descubrieron varias formas de construir cuadrados mágicos simples para órdenes impares y par-par; el caso más difícil del caso par-impar ( n = 4k + 2 ) fue resuelto por Ibn al-Haytham con k par (c. 1040), y completamente a principios del siglo XII, si no ya en la segunda mitad del siglo XI. [22] Casi al mismo tiempo, se estaban construyendo cuadrados pandiagonales. Los tratados sobre cuadrados mágicos fueron numerosos en los siglos XI y XII. Estos desarrollos posteriores tendieron a ser mejoras o simplificaciones de los métodos existentes. A partir del siglo XIII, los cuadrados mágicos se utilizaron cada vez más con fines ocultistas. [22] Sin embargo, muchos de estos textos posteriores escritos con fines ocultistas simplemente representan ciertos cuadrados mágicos y mencionan sus atributos, sin describir su principio de construcción, y solo algunos autores mantuvieron viva la teoría general. [22] Uno de estos ocultistas fue el argelino Ahmad al-Buni (c. 1225), que dio métodos generales para construir cuadrados mágicos con bordes; otros fueron el egipcio del siglo XVII Shabramallisi y el nigeriano del siglo XVIII al-Kishnawi. [27]
El cuadrado mágico de orden tres fue descrito como un amuleto para la procreación [28] [29] desde sus primeras apariciones literarias en las obras alquímicas de Jābir ibn Hayyān (fl. c. 721 – c. 815) [29] [30] y al-Ghazālī (1058–1111) [31] y fue preservado en la tradición de las tablas planetarias. La primera aparición de la asociación de siete cuadrados mágicos con las virtudes de los siete cuerpos celestes aparece en el Kitāb tadbīrāt al-kawākib ( Libro sobre las influencias de los planetas ) del erudito andaluz Ibn Zarkali (conocido como Azarquiel en Europa) (1029–1087) . [32] Un siglo después, el erudito argelino Ahmad al-Buni atribuyó propiedades místicas a los cuadrados mágicos en su influyente libro Shams al-Ma'arif ( El libro del sol de la gnosis y las sutilezas de las cosas elevadas ), que también describe su construcción. Esta tradición sobre una serie de cuadrados mágicos del orden tres al nueve, que están asociados con los siete planetas, sobrevive en versiones griegas, árabes y latinas. [33] También hay referencias al uso de cuadrados mágicos en cálculos astrológicos, una práctica que parece haberse originado con los árabes. [34] [35]

A diferencia de lo que ocurrió en Persia y Arabia, existe una mejor documentación sobre cómo se transmitieron los cuadrados mágicos a Europa. Alrededor de 1315, influenciado por fuentes árabes, el erudito bizantino griego Manuel Moschopoulos escribió un tratado matemático sobre el tema de los cuadrados mágicos, dejando de lado el misticismo de sus predecesores de Oriente Medio, donde dio dos métodos para los cuadrados impares y dos métodos para los cuadrados pares. Moschopoulos fue esencialmente desconocido para la Europa latina hasta finales del siglo XVII, cuando Philippe de la Hire redescubrió su tratado en la Biblioteca Real de París. [36] Sin embargo, no fue el primer europeo en escribir sobre los cuadrados mágicos; y los cuadrados mágicos se difundieron al resto de Europa a través de España e Italia como objetos ocultos. Los primeros tratados ocultistas que mostraban los cuadrados no describían cómo se construían. Por lo tanto, la teoría completa tuvo que ser redescubierta.
Los cuadrados mágicos aparecieron por primera vez en Europa en Kitāb tadbīrāt al-kawākib ( Libro sobre las influencias de los planetas ) escrito por Ibn Zarkali de Toledo, Al-Andalus, como cuadrados planetarios en el siglo XI. [32] El cuadrado mágico de tres fue discutido de manera numerológica a principios del siglo XII por el erudito judío Abraham ibn Ezra de Toledo, lo que influyó en los cabalistas posteriores. [37] La obra de Ibn Zarkali fue traducida como Libro de Astromagia en la década de 1280, [38] debido a Alfonso X de Castilla. [39] [32] En el texto alfonsí, los cuadrados mágicos de diferentes órdenes se asignan a los respectivos planetas, como en la literatura islámica; desafortunadamente, de todos los cuadrados discutidos, el cuadrado mágico de Marte de orden cinco es el único cuadrado exhibido en el manuscrito. [40] [32]
Los cuadrados mágicos vuelven a aparecer en Florencia, Italia, en el siglo XIV. Un cuadrado de 6×6 y uno de 9×9 se exhiben en un manuscrito del Trattato d'Abbaco (Tratado del ábaco) de Paolo Dagomari . [41] [42] Es interesante observar que Paolo Dagomari, al igual que Pacioli después de él, se refiere a los cuadrados como una base útil para inventar juegos y cuestiones matemáticas, y no menciona ningún uso mágico. Sin embargo, por cierto, también se refiere a ellos como los cuadrados del Sol y de la Luna respectivamente, y menciona que entran en cálculos astrológicos que no están mejor especificados. Como se dijo, el mismo punto de vista parece motivar al compatriota florentino Luca Pacioli , quien describe cuadrados de 3×3 a 9×9 en su obra De Viribus Quantitatis a fines del siglo XV. [43] [44]

Los cuadrados planetarios se habían difundido en el norte de Europa a finales del siglo XV. Por ejemplo, el manuscrito de Cracovia de Picatrix de Polonia muestra cuadrados mágicos de órdenes 3 a 9. El mismo conjunto de cuadrados que en el manuscrito de Cracovia aparece más tarde en los escritos de Paracelso en Archidoxa Magica (1567), aunque en forma muy confusa. En 1514, Alberto Durero inmortalizó un cuadrado de 4 × 4 en su famoso grabado Melencolia I. El contemporáneo de Paracelso, Heinrich Cornelius Agrippa von Nettesheim, publicó su famoso libro de tres volúmenes De occulta philosophia en 1531, donde dedicó el Capítulo 22 del Libro II a los cuadrados planetarios que se muestran a continuación. [37] El mismo conjunto de cuadrados dados por Agrippa reaparece en 1539 en Practica Arithmetice de Girolamo Cardano , donde explica la construcción de los cuadrados ordenados impares utilizando el "método del diamante", que luego fue reproducido por Bachet. [45] La tradición de los cuadrados planetarios fue continuada hasta el siglo XVII por Athanasius Kircher en Oedipi Aegyptici (1653). En Alemania, los tratados matemáticos sobre los cuadrados mágicos fueron escritos en 1544 por Michael Stifel en Arithmetica Integra , quien redescubrió los cuadrados bordeados, y Adam Riese , quien redescubrió el método de numeración continua para construir cuadrados ordenados impares publicados por Agrippa. Sin embargo, debido a las convulsiones religiosas de esa época, estos trabajos eran desconocidos para el resto de Europa. [37]
En Francia, en 1624, Claude Gaspard Bachet describió el "método del diamante" para construir los cuadrados ordenados impares de Agripa en su libro Problèmes Plaisants . Durante 1640, Bernard Frenicle de Bessy y Pierre Fermat intercambiaron cartas sobre cuadrados y cubos mágicos, y en una de las cartas Fermat se jacta de ser capaz de construir 1.004.144.995.344 cuadrados mágicos de orden 8 con su método. [45] Antoine Arnauld dio un relato temprano sobre la construcción de cuadrados con borde en su Nouveaux éléments de géométrie (1667). [46] En los dos tratados Des quarrez ou tables magiques y Table générale des quarrez magiques de quatre de côté , publicados póstumamente en 1693, veinte años después de su muerte, Bernard Frenicle de Bessy demostró que había exactamente 880 cuadrados mágicos distintos de orden cuatro. Frenicle proporcionó métodos para construir cuadrados mágicos de cualquier orden par e impar, donde los cuadrados de orden par se construían utilizando bordes. También demostró que intercambiar filas y columnas de un cuadrado mágico producía nuevos cuadrados mágicos. [45] En 1691, Simon de la Loubère describió el método continuo indio de construcción de cuadrados mágicos de orden impar en su libro Du Royaume de Siam , que había aprendido mientras regresaba de una misión diplomática a Siam, que era más rápido que el método de Bachet. En un intento de explicar su funcionamiento, de la Loubère utilizó los números primarios y los números raíz, y redescubrió el método de sumar dos cuadrados preliminares. Este método fue investigado más a fondo por el abad Poignard en el Traité des quarrés sublimes (1704), por Philippe de La Hire en Mémoires de l'Académie des Sciences para la Royal Academy (1705), y por Joseph Sauveur en Construction des quarrés magiques (1710). Los cuadrados concéntricos con bordes también fueron estudiados por De la Hire en 1705, mientras que Sauveur introdujo los cubos mágicos y los cuadrados con letras, que fueron retomados más tarde por Euler en 1776, a quien a menudo se le atribuye el mérito de idearlos. En 1750, d'Ons-le-Bray redescubrió el método de construcción de cuadrados doblemente pares y simplemente pares utilizando la técnica de los bordes; mientras que en 1767, Benjamin Franklin publicó un cuadrado semimágico que tenía las propiedades del cuadrado de Franklin epónimo. [47] En ese momento, el misticismo anterior asociado a los cuadrados mágicos había desaparecido por completo y el tema fue tratado como parte de las matemáticas recreativas. [37] [48]
En el siglo XIX, Bernard Violle trató exhaustivamente los cuadrados mágicos en su obra de tres volúmenes Traité complet des carrés magiques (1837-1838), en la que también describía los cubos mágicos, los paralelogramos, los paralelepípedos y los círculos. Los cuadrados pandiagonales fueron estudiados extensamente por Andrew Hollingworth Frost, que los aprendió mientras estaba en la ciudad de Nasik, India (por eso los llamó cuadrados de Nasik) en una serie de artículos: On the knight's path (1877), On the General Properties of Nasik Squares (1878), On the General Properties of Nasik Cubes (1878), On the construction of Nasik Squares of any order (1896). Demostró que es imposible tener cuadrados mágicos pandiagonales normales y pares. Frederick AP Barnard construyó cuadrados mágicos incrustados y otras figuras mágicas tridimensionales como esferas mágicas y cilindros mágicos en Theory of magic squares and of magic cubes (1888). [48] En 1897, Emroy McClintock publicó Sobre la forma más perfecta de los cuadrados mágicos , acuñando las palabras cuadrado pandiagonal y cuadrado más perfecto , que anteriormente se habían denominado perfecto, o diabólico, o Nasik.

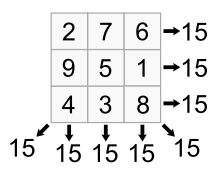
Leyendas que datan de tan temprano como 650 a. C. cuentan la historia del Lo Shu (洛書) o "rollo del río Lo". [8] Según la leyenda, en una época en la antigua China hubo una gran inundación. Mientras el gran rey Yu intentaba canalizar el agua hacia el mar, una tortuga emergió de ella con un curioso patrón en su caparazón: una cuadrícula de 3 × 3 en la que se disponían puntos circulares de números, de modo que la suma de los números en cada fila, columna y diagonal era la misma: 15. Según la leyenda, a partir de entonces la gente pudo usar este patrón de cierta manera para controlar el río y protegerse de las inundaciones [ cita requerida ] . El cuadrado Lo Shu , como se llama al cuadrado mágico en el caparazón de la tortuga, es el único cuadrado mágico normal de orden tres en el que 1 está en la parte inferior y 2 en la esquina superior derecha. Cada cuadrado mágico normal de orden tres se obtiene del Lo Shu por rotación o reflexión.

Hay un conocido cuadrado mágico normal de 4×4 del siglo XII inscrito en la pared del templo Parshvanath en Khajuraho , India. [18] [17] [49]
Este se conoce como Chautisa Yantra ( Chautisa , 34; Yantra , lit. "dispositivo"), ya que su suma mágica es 34. Es uno de los tres cuadrados mágicos pandiagonales de 4×4 y también es un ejemplo del cuadrado mágico más perfecto . El estudio de este cuadrado llevó a la apreciación de los cuadrados pandiagonales por parte de los matemáticos europeos a fines del siglo XIX. Los cuadrados pandiagonales se denominaban cuadrados Nasik o cuadrados Jain en la literatura inglesa más antigua.
.jpg/440px-Albrecht_Dürer_-_Melencolia_I_(detail).jpg)
Se cree que el cuadrado mágico normal de orden cuatro que Alberto Durero inmortalizó en su grabado de 1514 Melencolia I , mencionado anteriormente, es el primero que se vio en el arte europeo. El cuadrado asociado con Júpiter aparece como un talismán utilizado para alejar la melancolía. Es muy similar al cuadrado de Yang Hui , que se creó en China unos 250 años antes de la época de Durero. Como ocurre con todos los cuadrados mágicos normales de orden cuatro, la suma mágica es 34. Pero en el cuadrado de Durero esta suma también se encuentra en cada uno de los cuadrantes, en los cuatro cuadrados centrales y en los cuadrados de las esquinas (tanto de la cuadrícula de 4x4 como de las cuatro cuadrículas de 3x3 que contenía). Esta suma también se puede encontrar en los cuatro números exteriores en el sentido de las agujas del reloj desde las esquinas (3+8+14+9) y también en los cuatro en el sentido contrario a las agujas del reloj (las ubicaciones de las cuatro reinas en las dos soluciones del rompecabezas de las 4 reinas [50] ), los dos conjuntos de cuatro números simétricos (2+8+9+15 y 3+5+12+14), la suma de las dos entradas centrales de las dos columnas y filas externas (5+9+8+12 y 3+2+15+14), y en cuatro cuartetos con forma de cometa o cruz (3+5+11+15, 2+10+8+14, 3+9+7+15 y 2+6+12+14). Los dos números en el medio de la fila inferior dan la fecha del grabado: 1514. Se ha especulado que los números 4,1 que bordean la fecha de publicación corresponden a las iniciales de Durero D,A. Pero si esa hubiera sido su intención, podría haber invertido el orden de las columnas 1 y 4 para lograr "A1514D" sin comprometer las propiedades del cuadrado.
El cuadrado mágico de Durero también puede extenderse a un cubo mágico. [51]

La fachada de la Pasión de la iglesia de la Sagrada Familia en Barcelona , conceptualizada por Antoni Gaudí y diseñada por el escultor Josep Subirachs , presenta un cuadrado mágico de orden trivial 4: La constante mágica del cuadrado es 33, la edad de Jesús en el momento de la Pasión . [52] Estructuralmente, es muy similar al cuadrado mágico Melancolía , pero se han reducido los números en cuatro de las celdas en 1.
Los cuadrados triviales como éste no suelen ser matemáticamente interesantes y sólo tienen importancia histórica. Lee Sallows ha señalado que, debido a la ignorancia de Subirachs sobre la teoría de los cuadrados mágicos, el famoso escultor cometió un error innecesario, y apoya esta afirmación dando varios ejemplos de cuadrados mágicos 4×4 no triviales que muestran la constante mágica deseada de 33. [53]
De manera similar al cuadrado mágico de Durero, el cuadrado mágico de la Sagrada Familia también puede extenderse a un cubo mágico. [54]
El cuadrado de Parker , llamado así por el matemático recreativo Matt Parker , [55] es un intento de crear un cuadrado mágico de cuadrados de 3 × 3, un problema sin resolver muy apreciado desde Euler . [56] El cuadrado de Parker es un cuadrado semimágico trivial ya que utiliza algunos números más de una vez, y la diagonal 23 2 + 37 2 + 47 2 suma4107 , no3051 en cuanto a todas las demás filas y columnas, y la otra diagonal. El cuadrado de Parker se hizo popular en la cultura matemática. [ cita requerida ] El cuadrado de Parker se convirtió en una "mascota para la gente que lo intenta, pero al final fracasa". [ 57 ] [ se necesita una mejor fuente ]
El cuadrado de Gardner, llamado así en honor al matemático recreativo Martin Gardner , similar al cuadrado de Parker, se plantea como un problema para determinar a, b, c y d. [ cita requerida ]
Esta solución para a = 74, b = 113, c = 94 y d = 97 da un cuadrado semimágico; la diagonal 127 2 + b 2 + d 2 suma38 307 , no21 609 como para todas las demás filas y columnas, y la otra diagonal. [58] [59] [60]
La constante que es la suma de cualquier fila, columna o diagonal se llama constante mágica o suma mágica, M. Todo cuadrado mágico normal tiene una constante que depende del orden n , calculada mediante la fórmula . Esto se puede demostrar observando que la suma de es . Como la suma de cada fila es , la suma de filas es , que cuando se divide por el orden n da como resultado la constante mágica como . Para los cuadrados mágicos normales de órdenes n = 3, 4, 5, 6, 7 y 8, las constantes mágicas son, respectivamente: 15, 34, 65, 111, 175 y 260 (secuencia A006003 en la OEIS ).
El cuadrado mágico 1×1, con una sola celda que contiene el número 1, se llama trivial , porque normalmente no se lo considera cuando se habla de cuadrados mágicos; pero de hecho es un cuadrado mágico por definición, si una sola celda se considera como un cuadrado de orden uno.
Se pueden construir cuadrados mágicos normales de todos los tamaños excepto 2×2 (es decir, donde el orden n = 2). [61]
Si los números en el cuadrado mágico se ven como masas ubicadas en varias celdas, entonces el centro de masa de un cuadrado mágico coincide con su centro geométrico.
El momento de inercia de un cuadrado mágico se ha definido como la suma de todas las celdas del número en la celda multiplicado por el cuadrado de la distancia desde el centro de la celda hasta el centro del cuadrado; aquí la unidad de medida es el ancho de una celda. [62] (Así, por ejemplo, una celda de esquina de un cuadrado de 3×3 tiene una distancia de 1, una celda de borde que no es de esquina tiene una distancia de 1, y la celda del centro tiene una distancia de 0). Entonces, todos los cuadrados mágicos de un orden dado tienen el mismo momento de inercia entre sí. Para el caso de orden 3, el momento de inercia es siempre 60, mientras que para el caso de orden 4, el momento de inercia es siempre 340. En general, para el caso n × n , el momento de inercia es [62]
Dividiendo cada número del cuadrado mágico por la constante mágica se obtendrá una matriz doblemente estocástica , cuyas sumas de filas y columnas son iguales a la unidad. Sin embargo, a diferencia de la matriz doblemente estocástica, las sumas diagonales de dichas matrices también serán iguales a la unidad. Por lo tanto, dichas matrices constituyen un subconjunto de la matriz doblemente estocástica. El teorema de Birkhoff-von Neumann establece que para cualquier matriz doblemente estocástica , existen números reales , donde y matrices de permutación tales que
Esta representación puede no ser única en general. Sin embargo, según el teorema de Marcus-Ree, no es necesario que haya más de términos en cualquier descomposición. [63] Claramente, esta descomposición también se aplica a los cuadrados mágicos, ya que un cuadrado mágico se puede recuperar de una matriz doblemente estocástica multiplicándola por la constante mágica.

Si bien la clasificación de los cuadrados mágicos se puede realizar de muchas maneras, a continuación se ofrecen algunas categorías útiles. Una matriz cuadrada de n × n de números enteros 1, 2, ..., n 2 se denomina:
Sólo existe un cuadrado mágico (trivial) de orden 1 y ningún cuadrado mágico de orden 2. Como se mencionó anteriormente, el conjunto de cuadrados normales de orden tres constituye una única clase de equivalencia , todos equivalentes al cuadrado de Lo Shu. Por lo tanto, básicamente sólo existe un cuadrado mágico normal de orden 3.
El número de cuadrados mágicos n × n diferentes para n de 1 a 6, sin contar rotaciones y reflexiones es:
El número para n = 6 se había estimado previamente en (1,7745 ± 0,0016) × 10 19 . [64] [65] [62]
En relación con la secuencia anterior, una nueva clasificación enumera los toros mágicos que muestran estos cuadrados mágicos. El número de toros mágicos de orden n de 1 a 5 es:
El número de cuadrados mágicos normales distintos aumenta rápidamente para órdenes superiores. [66]
Los 880 cuadrados mágicos de orden 4 se muestran en 255 toros mágicos de orden 4 y los 275.305.224 cuadrados de orden 5 se muestran en 251.449.712 toros mágicos de orden 5. Todavía no se conocen los números de toros mágicos y cuadrados normales distintos para órdenes más allá de 5 y 6, respectivamente. [67] [ cita requerida ]
Los algoritmos tienden a generar únicamente cuadrados mágicos de un cierto tipo o clasificación, lo que hace que contar todos los cuadrados mágicos posibles sea bastante difícil. Dado que los métodos de conteo tradicionales han demostrado ser infructuosos, se ha aplicado el análisis estadístico mediante el método de Monte Carlo . El principio básico aplicado a los cuadrados mágicos es generar aleatoriamente matrices n × n de elementos del 1 al n 2 y verificar si el resultado es un cuadrado mágico. Luego se utiliza la probabilidad de que una matriz de números generada aleatoriamente sea un cuadrado mágico para aproximar el número de cuadrados mágicos. [68]
Versiones más complejas del método de Monte Carlo, como el método de Monte Carlo de intercambio y el método de Monte Carlo de retroceso, han producido estimaciones aún más precisas. Con estos métodos se ha demostrado que la probabilidad de cuadrados mágicos disminuye rápidamente a medida que n aumenta. Con el uso de funciones de ajuste se obtienen las curvas que se ven a la derecha.
A lo largo de los milenios se han descubierto muchas formas de construir cuadrados mágicos. Estos métodos se pueden clasificar como métodos generales y métodos especiales, en el sentido de que los métodos generales nos permiten construir más de un cuadrado mágico de un orden determinado, mientras que los métodos especiales nos permiten construir solo un cuadrado mágico de un orden determinado. Los métodos especiales son algoritmos específicos, mientras que los métodos generales pueden requerir algo de ensayo y error.
Los métodos especiales son las formas más sencillas de construir cuadrados mágicos. Siguen ciertos algoritmos que generan patrones regulares de números en un cuadrado. La exactitud de estos métodos especiales se puede demostrar utilizando uno de los métodos generales que se dan en secciones posteriores. Después de que se ha construido un cuadrado mágico utilizando un método especial, las transformaciones descritas en la sección anterior se pueden aplicar para producir más cuadrados mágicos. Los métodos especiales suelen mencionarse utilizando el nombre del autor (si se conoce) que describió el método, por ejemplo, el método de De la Loubere, el método de Starchey, el método de Bachet, etc.
Se cree que existen cuadrados mágicos para todos los órdenes, excepto para el orden 2. Los cuadrados mágicos se pueden clasificar según su orden como impares, doblemente pares ( n divisible por cuatro) y simplemente pares ( n par, pero no divisible por cuatro). Esta clasificación se basa en el hecho de que se deben emplear técnicas completamente diferentes para construir estos diferentes tipos de cuadrados. Los cuadrados mágicos impares y doblemente pares son fáciles de generar; la construcción de cuadrados mágicos simplemente pares es más difícil, pero existen varios métodos, incluido el método LUX de John Horton Conway para cuadrados mágicos y el método Strachey para cuadrados mágicos .
En el siglo XIX, Édouard Lucas ideó la fórmula general de los cuadrados mágicos de orden 3. Consideremos la siguiente tabla formada por los números enteros positivos a , b y c :
Estos nueve números serán enteros positivos distintos que forman un cuadrado mágico con la constante mágica 3 c siempre que 0 < a < b < c − a y b ≠ 2 a . Además, todo cuadrado mágico 3×3 de enteros positivos distintos tiene esta forma.
En 1997, Lee Sallows descubrió que, dejando de lado las rotaciones y las reflexiones, cada paralelogramo distinto dibujado en el diagrama de Argand define un cuadrado mágico único de 3×3, y viceversa, un resultado que nunca antes se había observado. [70]
Un método para construir cuadrados mágicos de orden impar fue publicado por el diplomático francés de la Loubère en su libro, Una nueva relación histórica del reino de Siam (Du Royaume de Siam, 1693), en el capítulo titulado El problema del cuadrado mágico según los indios . [73] El método funciona de la siguiente manera:
El método prescribe comenzar en la columna central de la primera fila con el número 1. Después de eso, el movimiento fundamental para llenar los cuadrados es diagonalmente hacia arriba y hacia la derecha, un paso a la vez. Si un cuadrado se llena con un múltiplo del orden n , uno se mueve verticalmente hacia abajo un cuadrado, luego continúa como antes. Cuando un movimiento "hacia arriba y hacia la derecha" dejaría el cuadrado, se envuelve hasta la última fila o la primera columna, respectivamente.
Es posible empezar desde otros cuadrados en lugar de la columna central de la primera fila, pero entonces solo las sumas de las filas y las columnas serán idénticas y darán como resultado una suma mágica, mientras que las sumas diagonales serán diferentes. El resultado será, por tanto, un cuadrado semimágico y no un cuadrado mágico verdadero. Moverse en direcciones distintas a la del noreste también puede dar como resultado cuadrados mágicos.
Doblemente par significa que n es un múltiplo par de un entero par; o 4 p (por ejemplo, 4, 8, 12), donde p es un entero.
Patrón genérico Todos los números se escriben en orden de izquierda a derecha en cada fila, comenzando por la esquina superior izquierda. Luego, los números se mantienen en el mismo lugar o se intercambian con sus números diametralmente opuestos en un patrón regular determinado. En el cuadrado mágico de orden cuatro, los números en los cuatro cuadrados centrales y un cuadrado en cada esquina se mantienen en el mismo lugar y los demás se intercambian con sus números diametralmente opuestos.
Construcción de un cuadrado mágico de orden 4 Empezando desde la parte superior izquierda, recorra de izquierda a derecha cada fila del cuadrado, contando cada celda del 1 al 16 y llenando las celdas a lo largo de las diagonales con su número correspondiente. Una vez que llegue a la celda inferior derecha, continúe yendo de derecha a izquierda, comenzando desde la parte inferior derecha de la tabla a través de cada fila, y complete las celdas no diagonales contando del 1 al 16 con su número correspondiente. Como se muestra a continuación:
Una extensión del ejemplo anterior para los órdenes 8 y 12 Primero genere una tabla de patrones, donde un '1' indica seleccionar del cuadrado donde los números están escritos en orden 1 a n 2 (de izquierda a derecha, de arriba a abajo), y un '0' indica seleccionar del cuadrado donde los números están escritos en orden inverso n 2 a 1. Para M = 4, la tabla de patrones es como se muestra a continuación (tercera matriz desde la izquierda). Con las celdas inalteradas (celdas con '1') sombreadas, se obtiene un patrón entrecruzado.
Los patrones son a) hay igual número de '1' y '0' en cada fila y columna; b) cada fila y cada columna son "palindrómicas"; c) las mitades izquierda y derecha son imágenes especulares; y d) las mitades superior e inferior son imágenes especulares (c y d implican b). La tabla de patrones se puede denotar usando hexadecimales como (9, 6, 6, 9) para simplificar (1 nibble por fila, 4 filas). El método más simple de generar el patrón requerido para cuadrados doblemente pares de orden superior es copiar el patrón genérico para el cuadrado de cuarto orden en cada subcuadrado de cuatro por cuatro.
Para M = 8, las posibles opciones para el patrón son (99, 66, 66, 99, 99, 66, 66, 99); (3C, 3C, C3, C3, C3, C3, 3C, 3C); (A5, 5A, A5, 5A, 5A, A5, 5A, A5) (2 mordiscos por fila, 8 filas).
Para M = 12, la tabla de patrones (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) produce un cuadrado mágico (3 nibbles por fila, 12 filas). Es posible contar la cantidad de opciones que uno tiene basándose en la tabla de patrones, teniendo en cuenta las simetrías rotacionales.
El primer descubrimiento del método de superposición lo realizó el matemático indio Narayana en el siglo XIV. El mismo método fue redescubierto y estudiado posteriormente en Europa a principios del siglo XVIII por de la Loubere, Poignard, de La Hire y Sauveur; y el método suele denominarse método de de la Hire. Aunque el trabajo de Euler sobre el cuadrado mágico no fue original, es famoso por su conjetura sobre la imposibilidad de construir cuadrados grecolatinos mutuamente ortogonales ordenados con números pares impares . Esta conjetura fue refutada a mediados del siglo XX. Para mayor claridad de la exposición, se pueden distinguir dos variaciones importantes de este método.
Este método consiste en construir dos cuadrados preliminares, que al sumarse dan el cuadrado mágico. Como ejemplo práctico, se considera un cuadrado mágico de 3×3. Cada número del cuadrado natural de 3×3 por un par de números se puede etiquetar como
donde cada par de alfabetos griego y latino, p. ej. αa , se deben sumar, es decir αa = α + a . Aquí, ( α , β , γ ) = (0, 3, 6) y ( a , b , c ) = (1, 2, 3). Los números 0, 3 y 6 se denominan números raíz, mientras que los números 1, 2 y 3 se denominan números primarios . Una restricción general importante aquí es
De esta forma, el cuadrado original se puede dividir ahora en dos cuadrados más simples:
Los cuadrados con letras se denominan cuadrados griegos o cuadrados latinos si están llenos de letras griegas o latinas, respectivamente. Se puede construir un cuadrado mágico asegurándose de que los cuadrados griegos y latinos también sean cuadrados mágicos. La inversa de esta afirmación también es a menudo, pero no siempre (por ejemplo, cuadrados mágicos con borde), cierta: un cuadrado mágico se puede descomponer en un cuadrado griego y un cuadrado latino, que son a su vez cuadrados mágicos. Por lo tanto, el método es útil tanto para la síntesis como para el análisis de un cuadrado mágico. Por último, al examinar el patrón en el que se disponen los números en el cuadrado terminado, a menudo es posible idear un algoritmo más rápido para construir cuadrados de orden superior que repliquen el patrón dado, sin la necesidad de crear los cuadrados griegos y latinos preliminares.
Durante la construcción del cuadrado mágico 3×3, los cuadrados griego y latino con sólo tres términos únicos son mucho más fáciles de manejar que el cuadrado original con nueve términos diferentes. La suma de las filas y la suma de las columnas del cuadrado griego serán las mismas, α + β + γ , si
Esto se puede lograr mediante la permutación cíclica de α , β y γ . La satisfacción de estas dos condiciones garantiza que el cuadrado resultante sea un cuadrado semimágico; y se dice que estos cuadrados griegos y latinos son mutuamente ortogonales entre sí. Para un orden dado n , hay como máximo n - 1 cuadrados en un conjunto de cuadrados mutuamente ortogonales, sin contar las variaciones debidas a la permutación de los símbolos. Este límite superior es exacto cuando n es un número primo.
Para construir un cuadrado mágico, también debemos asegurarnos de que las diagonales sumen una constante mágica. Para ello, tenemos una tercera condición:
Los cuadrados griegos y latinos mutuamente ortogonales que satisfacen la primera parte de la tercera condición (que todas las letras aparezcan en ambas diagonales) se dicen que son cuadrados grecolatinos doblemente diagonales mutuamente ortogonales .
Cuadrados impares: Para el cuadrado impar 3×3, dado que α , β y γ están en progresión aritmética, su suma es igual al producto del orden del cuadrado por el término medio, es decir α + β + γ = 3 β . Por lo tanto, las sumas diagonales serán iguales si tenemos β s en la diagonal principal y α , β , γ en la diagonal oblicua. De manera similar, para el cuadrado latino. Los cuadrados griego y latino resultantes y su combinación serán los siguientes. El cuadrado latino es simplemente una rotación de 90 grados en sentido antihorario del cuadrado griego (o equivalentemente, volteándolo sobre el eje vertical) con las letras correspondientes intercambiadas. Sustituir los valores de las letras griegas y latinas dará como resultado el cuadrado mágico 3×3.
En el caso de los cuadrados impares, este método explica por qué funcionan el método siamés (método de De la Loubere) y sus variantes. Este método básico se puede utilizar para construir cuadrados mágicos impares ordenados de órdenes superiores. En resumen:
Una peculiaridad del método de construcción dado anteriormente para los cuadrados mágicos impares es que el número medio ( n 2 + 1)/2 siempre aparecerá en la celda central del cuadrado mágico. Como hay ( n - 1)! formas de ordenar los términos de la diagonal oblicua, podemos obtener ( n - 1)! cuadrados griegos de esta manera; lo mismo con los cuadrados latinos. Además, como cada cuadrado griego puede emparejarse con ( n - 1)! cuadrados latinos, y como para cada cuadrado griego el término medio puede ubicarse arbitrariamente en la diagonal principal o en la diagonal oblicua (y correspondientemente a lo largo de la diagonal oblicua o la diagonal principal para los cuadrados latinos), podemos construir un total de 2 × ( n - 1)! × ( n - 1)! cuadrados mágicos usando este método. Para n = 3, 5 y 7, esto dará 8, 1152 y 1.036.800 cuadrados mágicos diferentes, respectivamente. Dividiendo por 8 para descuidar los cuadrados equivalentes debidos a la rotación y las reflexiones, obtenemos 1, 144 y 129,600 cuadrados mágicos esencialmente diferentes, respectivamente.
Como otro ejemplo, se da la construcción de un cuadrado mágico de 5x5. Los números se escriben directamente en lugar de las letras. Los cuadrados numerados se denominan cuadrado primario o cuadrado raíz si están llenos de números primarios o números raíz, respectivamente. Los números se colocan sobre la diagonal oblicua en el cuadrado raíz de modo que la columna central del cuadrado raíz resultante tenga 0, 5, 10, 15, 20 (de abajo hacia arriba). El cuadrado primario se obtiene rotando el cuadrado raíz en sentido antihorario 90 grados y reemplazando los números. El cuadrado resultante es un cuadrado mágico asociativo, en el que cada par de números simétricamente opuestos al centro suman el mismo valor, 26. Por ejemplo, 16+10, 3+23, 6+20, etc. En el cuadrado terminado, se coloca 1 en la celda central de la fila inferior y los números sucesivos se colocan mediante un movimiento alargado del caballo (dos celdas a la derecha, dos celdas hacia abajo) o, equivalentemente, el movimiento del alfil (dos celdas en diagonal hacia abajo a la derecha). Cuando se produce una colisión, el movimiento de ruptura consiste en desplazarse una casilla hacia arriba. Todos los números impares se encuentran dentro del rombo central formado por 1, 5, 25 y 21, mientras que los números pares se colocan en las esquinas. La aparición de los números pares se puede deducir copiando el cuadrado a los lados adyacentes. Los números pares de cuatro cuadrados adyacentes formarán una cruz.
A continuación se muestra una variación del ejemplo anterior, en el que la secuencia diagonal oblicua se toma en un orden diferente. El cuadrado mágico resultante es la versión invertida del famoso cuadrado mágico de Marte de Agripa. Es un cuadrado mágico asociativo y es el mismo que el producido por el método de Moschopoulos. Aquí el cuadrado resultante comienza con un 1 colocado en la celda que está a la derecha de la celda central y procede como el método de De la Loubere, con un movimiento de abajo a derecha. Cuando ocurre una colisión, el movimiento de ruptura consiste en desplazar dos celdas hacia la derecha.
En los ejemplos anteriores, para el cuadrado griego, la segunda fila se puede obtener a partir de la primera fila desplazándola circularmente una celda hacia la derecha. De manera similar, la tercera fila es una versión desplazada circularmente de la segunda fila una celda hacia la derecha, y así sucesivamente. Asimismo, las filas del cuadrado latino se desplazan circularmente una celda hacia la izquierda. Los desplazamientos de fila para los cuadrados griego y latino son en direcciones opuestas entre sí. Es posible desplazar circularmente las filas más de una celda para crear el cuadrado griego y latino.
Esto recrea esencialmente el movimiento del caballo. Todas las letras aparecerán en ambas diagonales, lo que garantiza una suma diagonal correcta. Dado que hay n ! permutaciones de las letras griegas con las que podemos crear la primera fila del cuadrado griego, hay n ! cuadrados griegos que se pueden crear desplazando la primera fila en una dirección. Del mismo modo, hay n ! cuadrados latinos creados desplazando la primera fila en la dirección opuesta. Dado que un cuadrado griego se puede combinar con cualquier cuadrado latino con desplazamientos de fila opuestos, hay n ! × n ! combinaciones de este tipo. Por último, dado que el cuadrado griego se puede crear desplazando las filas hacia la izquierda o hacia la derecha, hay un total de 2 × n ! × n ! cuadrados mágicos que se pueden formar con este método. Para n = 5 y 7, dado que son números primos, este método crea 28.800 y 50.803.200 cuadrados mágicos pandiagonales. Dividiendo por 8 para ignorar los cuadrados equivalentes debidos a la rotación y las reflexiones, obtenemos 3.600 y 6.350.400 cuadrados equivalentes. Dividiendo por n 2 para ignorar los cuadrados panmágicos equivalentes debido al desplazamiento cíclico de filas o columnas, obtenemos 144 y 129.600 cuadrados panmágicos esencialmente diferentes. Para los cuadrados de orden 5, estos son los únicos cuadrados panmágicos que existen. La condición de que el orden del cuadrado no sea divisible por 3 significa que no podemos construir cuadrados de órdenes 9, 15, 21, 27, etc., mediante este método.
En el ejemplo siguiente, el cuadrado se ha construido de forma que el 1 se encuentra en la celda central. En el cuadrado terminado, los números se pueden enumerar de forma continua mediante el movimiento del caballo (dos celdas hacia arriba, una celda a la derecha). Cuando se produce una colisión, el movimiento de ruptura consiste en mover una celda hacia arriba y una celda a la izquierda. El cuadrado resultante es un cuadrado mágico pandiagonal. Este cuadrado también tiene otra propiedad diabólica: cualesquiera cinco celdas en patrón quincuncial formadas por cualquier subcuadrado impar, incluido el envolvente, suman la constante mágica, 65. Por ejemplo, 13+7+1+20+24, 23+1+9+15+17, 13+21+10+19+2, etc. Además, las cuatro esquinas de cualquier cuadrado de 5 × 5 y la celda central, así como las celdas del medio de cada lado junto con la celda central, incluido el envolvente, dan la suma mágica: 13+10+19+22+1 y 20+24+12+8+1. Por último los cuatro romboides que forman cruces alargadas también dan la suma mágica: 23+1+9+24+8, 15+1+17+20+12, 14+1+18+13+19, 7+1+25+22+10.
También podemos combinar los cuadrados griegos y latinos construidos por diferentes métodos. En el ejemplo siguiente, el cuadrado primario se forma utilizando el movimiento del caballo. Hemos recreado el cuadrado mágico obtenido por el método de De la Loubere. Como antes, podemos formar 8 × ( n - 1)! × n ! cuadrados mágicos mediante esta combinación. Para n = 5 y 7, esto creará 23.040 y 29.030.400 cuadrados mágicos. Después de dividir por 8 para descuidar los cuadrados equivalentes debido a la rotación y la reflexión, obtenemos 2.880 y 3.628.800 cuadrados.
Para los cuadrados de orden 5, estos tres métodos dan un censo completo del número de cuadrados mágicos que se pueden construir mediante el método de superposición. Despreciando la rotación y las reflexiones, el número total de cuadrados mágicos de orden 5 producidos por el método de superposición es 144 + 3600 + 2880 = 6624.
Cuadrados pares: También podemos construir cuadrados pares ordenados de esta manera. Como no existe un término medio entre los alfabetos griego y latino para los cuadrados pares ordenados, además de las dos primeras restricciones, para que las sumas diagonales den como resultado la constante mágica, todas las letras del alfabeto deben aparecer en la diagonal principal y en la diagonal oblicua.
A continuación se muestra un ejemplo de un cuadrado de 4 × 4. Para la diagonal y la diagonal oblicua dadas en el cuadrado griego, el resto de las celdas se pueden completar utilizando la condición de que cada letra aparezca solo una vez en una fila y una columna.
Usando estos dos cuadrados grecolatinos, podemos construir 2 × 4! × 4! = 1,152 cuadrados mágicos. Dividiendo por 8 para eliminar los cuadrados equivalentes debidos a la rotación y las reflexiones, obtenemos 144 cuadrados mágicos esencialmente diferentes de orden 4. Estos son los únicos cuadrados mágicos que se pueden construir por el método de Euler, ya que solo hay dos cuadrados grecolatinos doblemente diagonales mutuamente ortogonales de orden 4.
De manera similar, se puede construir un cuadrado mágico de 8×8 como el que se muestra a continuación. En este caso, el orden de aparición de los números no es importante; sin embargo, los cuadrantes imitan el patrón de disposición de los cuadrados grecolatinos de 4×4.
El método de Euler ha dado origen al estudio de los cuadrados grecolatinos . El método de Euler para construir cuadrados mágicos es válido para cualquier orden excepto 2 y 6.
Variations: Magic squares constructed from mutually orthogonal doubly diagonal Graeco-Latin squares are interesting in themselves since the magic property emerges from the relative position of the alphabets in the square, and not due to any arithmetic property of the value assigned to them. This means that we can assign any value to the alphabets of such squares and still obtain a magic square. This is the basis for constructing squares that display some information (e.g. birthdays, years, etc.) in the square and for creating "reversible squares". For example, we can display the number π ≈ 3.141592 at the bottom row of a 4×4 magic square using the Graeco-Latin square given above by assigning (α, β, γ, δ) = (10, 0, 90, 15) and (a, b, c, d) = (0, 2, 3, 4). We will obtain the following non-normal magic square with the magic sum 124:
Narayana-De la Hire's method for odd square is the same as that of Euler's. However, for even squares, we drop the second requirement that each Greek and Latin letter appear only once in a given row or column. This allows us to take advantage of the fact that the sum of an arithmetic progression with an even number of terms is equal to the sum of two opposite symmetric terms multiplied by half the total number of terms. Thus, when constructing the Greek or Latin squares,
As a running example, if we take a 4×4 square, where the Greek and Latin terms have the values (α, β, γ, δ) = (0, 4, 8, 12) and (a, b, c, d) = (1, 2, 3, 4), respectively, then we have α + β + γ + δ = 2 (α + δ) = 2 (β + γ). Similarly, a + b + c + d = 2 (a + d) = 2 (b + c). This means that the complementary pair α and δ (or β and γ) can appear twice in a column (or a row) and still give the desired magic sum. Thus, we can construct:
In the example given below, the main diagonal (from top left to bottom right) is filled with sequence ordered as α, β, γ, δ, while the skew diagonal (from bottom left to top right) filled in the same order. The remaining cells are then filled column wise such that the complementary letters appears only once within a row, but twice within a column. In the first column, since α appears on the 1st and 4th row, the remaining cells are filled with its complementary term δ. Similarly, the empty cells in the 2nd column are filled with γ; in 3rd column β; and 4th column α. Each Greek letter appears only once along the rows, but twice along the columns. As such, the row sums are α + β + γ + δ while the column sums are either 2 (α + δ) or 2 (β + γ). Likewise for the Latin square, which is obtained by flipping the Greek square along the main diagonal and interchanging the corresponding letters.
The above example explains why the "criss-cross" method for doubly even magic square works. Another possible 4×4 magic square, which is also pan-diagonal as well as most-perfect, is constructed below using the same rule. However, the diagonal sequence is chosen such that all four letters α, β, γ, δ appear inside the central 2×2 sub-square. Remaining cells are filled column wise such that each letter appears only once within a row. In the 1st column, the empty cells need to be filled with one of the letters selected from the complementary pair α and δ. Given the 1st column, the entry in the 2nd row can only be δ since α is already there in the 2nd row; while, in the 3rd row the entry can only be α since δ is already present in the 3rd row. We proceed similarly until all cells are filled. The Latin square given below has been obtained by flipping the Greek square along the main diagonal and replacing the Greek alphabets with corresponding Latin alphabets.
We can use this approach to construct singly even magic squares as well. However, we have to be more careful in this case since the criteria of pairing the Greek and Latin alphabets uniquely is not automatically satisfied. Violation of this condition leads to some missing numbers in the final square, while duplicating others. Thus, here is an important proviso:
Below is a construction of a 6×6 magic square, where the numbers are directly given, rather than the alphabets. The second square is constructed by flipping the first square along the main diagonal. Here in the first column of the root square the 3rd cell is paired with its complement in the 4th cells. Thus, in the primary square, the numbers in the 1st and 6th cell of the 3rd row are same. Likewise, with other columns and rows. In this example the flipped version of the root square satisfies this proviso.
As another example of a 6×6 magic square constructed this way is given below. Here the diagonal entries are arranged differently. The primary square is constructed by flipping the root square about the main diagonal. In the second square the proviso for singly even square is not satisfied, leading to a non-normal magic square (third square) where the numbers 3, 13, 24, and 34 are duplicated while missing the numbers 4, 18, 19, and 33.
The last condition is a bit arbitrary and may not always need to be invoked, as in this example, where in the root square each cell is vertically paired with its complement:
As one more example, we have generated an 8×8 magic square. Unlike the criss-cross pattern of the earlier section for evenly even square, here we have a checkered pattern for the altered and unaltered cells. Also, in each quadrant the odd and even numbers appear in alternating columns.
Variations: A number of variations of the basic idea are possible: a complementary pair can appear n/2 times or less in a column. That is, a column of a Greek square can be constructed using more than one complementary pair. This method allows us to imbue the magic square with far richer properties. The idea can also be extended to the diagonals too. An example of an 8×8 magic square is given below. In the finished square each of four quadrants are pan-magic squares as well, each quadrant with same magic constant 130.
In this method, the objective is to wrap a border around a smaller magic square which serves as a core. Consider the 3×3 square for example. Subtracting the middle number 5 from each number 1, 2, ..., 9, we obtain 0, ± 1, ± 2, ± 3, and ± 4, which we will, for lack of better words, following S. Harry White, refer to as bone numbers. The magic constant of a magic square, which we will refer to as the skeleton square, made by these bone numbers will be zero since adding all the rows of a magic square will give nM = Σ k = 0; thus M = 0.
It is not difficult to argue that the middle number should be placed at the center cell: let x be the number placed in the middle cell, then the sum of the middle column, middle row, and the two diagonals give Σ k + 3 x = 4 M. Since Σ k = 3 M, we have x = M / 3. Here M = 0, so x = 0.
Putting the middle number 0 in the center cell, we want to construct a border such that the resulting square is magic. Let the border be given by:
Since the sum of each row, column, and diagonals must be a constant (which is zero), we have
Now, if we have chosen a, b, u, and v, then we have a* = - a, b* = - b, u* = - u, and v* = - v. This means that if we assign a given number to a variable, say a = 1, then its complement will be assigned to a*, i.e. a* = - 1. Thus out of eight unknown variables, it is sufficient to specify the value of only four variables. We will consider a, b, u, and v as independent variables, while a*, b*, u*, and v* as dependent variables. This allows us to consider a bone number ± x as a single number regardless of sign because (1) its assignment to a given variable, say a, will automatically imply that the same number of opposite sign will be shared with its complement a*, and (2) two independent variables, say a and b, cannot be assigned the same bone number. But how should we choose a, b, u, and v? We have the sum of the top row and the sum of the right column as
Since 0 is an even number, there are only two ways that the sum of three integers will yield an even number: 1) if all three were even, or 2) if two were odd and one was even. Since in our choice of numbers we only have two even non-zero number (± 2 and ± 4), the first statement is false. Hence, it must be the case that the second statement is true: that two of the numbers are odd and one even.
The only way that both the above two equations can satisfy this parity condition simultaneously, and still be consistent with the set of numbers we have, is when u and v are odd. For on the contrary, if we had assumed u and a to be odd and v to be even in the first equation, then u* = - u will be odd in the second equation, making b odd as well, in order to satisfy the parity condition. But this requires three odd numbers (u, a, and b), contradicting the fact that we only have two odd numbers (± 1 and ± 3) which we can use. This proves that the odd bone numbers occupy the corners cells. When converted to normal numbers by adding 5, this implies that the corners of a 3×3 magic square are all occupied by even numbers.
Thus, taking u = 1 and v = 3, we have a = - 4 and b = - 2. Hence, the finished skeleton square will be as in the left. Adding 5 to each number, we get the finished magic square.
Similar argument can be used to construct larger squares. Since there does not exist a 2×2 magic square around which we can wrap a border to construct a 4×4 magic square, the next smallest order for which we can construct bordered square is the order 5.
Consider the fifth-order square. For this, we have a 3×3 magic core, around which we will wrap a magic border. The bone numbers to be used will be ± 5, ± 6, ± 7, ± 8, ± 9, ± 10, ± 11, and ± 12. Disregarding the signs, we have 8 bone numbers, 4 of which are even and 4 of which are odd. In general, for a square of any order n, there will be 4(n - 1) border cells, which are to be filled using 2(n - 1) bone numbers. Let the magic border be given as
As before, we should
It is sufficient to determine the numbers u, v, a, b, c, d, e, f to describe the magic border. As before, we have the two constraint equations for the top row and right column:
Multiple solutions are possible. The standard procedure is to
There are 28 ways of choosing two numbers from the set of 8 bone numbers for the corner cells u and v. However, not all pairs are admissible. Among the 28 pairs, 16 pairs are made of an even and an odd number, 6 pairs have both as even numbers, while 6 pairs have them both as odd numbers.
We can prove that the corner cells u and v cannot have an even and an odd number. This is because if this were so, then the sums u + v and v + u* will be odd, and since 0 is an even number, the sums a + b + c and d + e + f should be odd as well. The only way that the sum of three integers will result in an odd number is when 1) two of them are even and one is odd, or 2) when all three are odd. Since the corner cells are assumed to be odd and even, neither of these two statements are compatible with the fact that we only have 3 even and 3 odd bone numbers at our disposal. This proves that u and v cannot have different parity. This eliminates 16 possibilities.
Using similar type reasoning we can also draw some conclusions about the sets {a, b, c} and {d, e, f}. If u and v are both even, then both the sets should have two odd numbers and one even number. If u and v are both odd, then one of the sets should have three even numbers while the other set should have one even number and two odd numbers.
As a running example, consider the case when both u and v are even. The 6 possible pairs are: (6, 8), (6, 10), (6, 12), (8, 10), (8, 12), and (10, 12). Since the sums u + v and v + u* are even, the sums a + b + c and d + e + f should be even as well. The only way that the sum of three integers will result in an even number is when 1) two of them are odd and one is even, or 2) when all three are even. The fact that the two corner cells are even means that we have only 2 even numbers at our disposal. Thus, the second statement is not compatible with this fact. Hence, it must be the case that the first statement is true: two of the three numbers should be odd, while one be even.
Now let a, b, d, e be odd numbers while c and f be even numbers. Given the odd bone numbers at our disposal: ± 5, ± 7, ± 9, and ± 11, their differences range from D = { ± 2, ± 4, ± 6} while their sums range from S = {± 12, ± 14, ± 16, ± 18, ± 20}. It is also useful to have a table of their sum and differences for later reference. Now, given the corner cells (u, v), we can check its admissibility by checking if the sums u + v + c and v + u* + f fall within the set D or S. The admissibility of the corner numbers is a necessary but not a sufficient condition for the solution to exist.
For example, if we consider the pair (u, v) = (8, 12), then u + v = 20 and v + u* = 6; and we will have ± 6 and ± 10 even bone numbers at our disposal. Taking c = ± 6, we have the sum u + v + c to be 26 and 14, depending on the sign of ± 6 taken, both of which do not fall within the sets D or S. Likewise, taking c = ± 10, we have the sum u + v + c to be 30 and 10, both of which again do not fall within the sets D or S. Thus, the pair (8, 12) is not admissible. By similar process of reasoning, we can also rule out the pair (6, 12).
As another example, if we consider the pair (u, v) = (10, 12), then u + v = 22 and v + u* = 2; and we will have ± 6 and ± 8 even bone numbers at our disposal. Taking c = ± 6, we have the sum u + v + c to be 28 and 16. While 28 does not fall within the sets D or S, 16 falls in set S. By inspection, we find that if (a, b) = (-7, -9), then a + b = -16; and it will satisfy the first constraint equation. Also, taking f = ± 8, we have the sum v + u* + f to be 10 and -6. While 10 does not fall within the sets D or S, -6 falls in set D. Since -7 and -9 have already been assigned to a and b, clearly (d, e) = (-5, 11) so that d + e = 6; and it will satisfy the second constraint equation.
Likewise, taking c = ± 8, we have the sum u + v + c to be 30 and 14. While 30 does not fall within the sets D or S, 14 falls in set S. By inspection, we find that if (a, b) = (-5, -9), then a + b = -14. Also, taking f = ± 6, we have the sum v + u* + f to be 8 and -4. While 8 does not fall within the sets D or S, -4 falls in set D. Clearly, (d, e) = (-7, 11) so that d + e = 4, and the second constraint equation will be satisfied.
Hence the corner pair (u, v) = (10, 12) is admissible; and it admits two solutions: (a, b, c, d, e, f) = (-7, -9, -6, -5, 11, -8) and (a, b, c, d, e, f) = ( -5, -9, -8, -7, 11, -6). The finished skeleton squares are given below. The magic square is obtained by adding 13 to each cells.
Using similar process of reasoning, we can construct the following table for the values of u, v, a, b, c, d, e, f expressed as bone numbers as given below. There are only 6 possible choices for the corner cells, which leads to 10 possible border solutions.
Given this group of 10 borders, we can construct 10×8×(3!)2 = 2880 essentially different bordered magic squares. Here the bone numbers ± 5, ..., ± 12 were consecutive. More bordered squares can be constructed if the numbers are not consecutive. If non-consecutive bone numbers were also used, then there are a total of 605 magic borders. Thus, the total number of order 5 essentially different bordered magic squares (with consecutive and non-consecutive numbers) is 174,240.[74][75] See history.[76] The number of fifth-order magic squares constructible via the bordering method is about 26 times larger than via the superposition method.
Exhaustive enumeration of all the borders of a magic square of a given order, as done previously, is very tedious. As such a structured solution is often desirable, which allows us to construct a border for a square of any order. Below we give three algorithms for constructing border for odd, doubly even, and singly even squares. These continuous enumeration algorithms were discovered in 10th century by Arab scholars; and their earliest surviving exposition comes from the two treatises by al-Buzjani and al-Antaki, although they themselves were not the discoverers.[24] Since then many more such algorithms have been discovered.
Odd-ordered squares: The following is the algorithm given by al-Buzjani to construct a border for odd squares. A peculiarity of this method is that for order n square, the two adjacent corners are numbers n - 1 and n + 1.
Starting from the cell above the lower left corner, we put the numbers alternately in left column and bottom row until we arrive at the middle cell. The next number is written in the middle cell of the bottom row just reached, after which we fill the cell in the upper left corner, then the middle cell of the right column, then the upper right corner. After this, starting from the cell above middle cell of the right column already filled, we resume the alternate placement of the numbers in the right column and the top row. Once half of the border cells are filled, the other half are filled by numbers complementary to opposite cells. The subsequent inner borders is filled in the same manner, until the square of order 3 is filled.[24]
Below is an example for 9th-order square.
Doubly even order: The following is the method given by al-Antaki. Consider an empty border of order n = 4k with k ≥ 3. The peculiarity of this algorithm is that the adjacent corner cells are occupied by numbers n and n - 1.
Starting at the upper left corner cell, we put the successive numbers by groups of four, the first one next to the corner, the second and the third on the bottom, and the fourth at the top, and so on until there remains in the top row (excluding the corners) six empty cells. We then write the next two numbers above and the next four below. We then fill the upper corners, first left then right. We place the next number below the upper right corner in the right column, the next number on the other side in the left column. We then resume placing groups of four consecutive numbers in the two columns as before. Once half of the border cells are filled, the other half are filled by numbers complementary to opposite cells.[24]
The example below gives the border for order 16 square.
For order 8 square, we just begin directly with the six cells.
Singly even order: For singly even order, we have the algorithm given by al-Antaki. Here the corner cells are occupied by n and n - 1. Below is an example of 10th-order square.
Start by placing 1 at the bottom row next to the left corner cell, then place 2 in the top row. After this, place 3 at the bottom row and turn around the border in anti-clockwise direction placing the next numbers, until n - 2 is reached on the right column. The next two numbers are placed in the upper corners (n - 1 in upper left corner and n in upper right corner). Then, the next two numbers are placed on the left column, then we resume the cyclic placement of the numbers until half of all the border cells are filled. Once half of the border cells are filled, the other half are filled by numbers complementary to opposite cells.[24]
This is a method reminiscent of the Kronecker product of two matrices, that builds an nm × nm magic square from an n × n magic square and an m × m magic square.[77] The "product" of two magic squares creates a magic square of higher order than the two multiplicands. Let the two magic squares be of orders m and n. The final square will be of order m × n. Divide the square of order m × n into m × m sub-squares, such that there are a total of n2 such sub-squares. In the square of order n, reduce by 1 the value of all the numbers. Multiply these reduced values by m2, and place the results in the corresponding sub-squares of the m × n whole square. The squares of order m are added n2 times to the sub-squares of the final square. The peculiarity of this construction method is that each magic subsquare will have different magic sums. The square made of such magic sums from each magic subsquare will again be a magic square. The smallest composite magic square of order 9, composed of two order 3 squares is given below.
Since each of the 3×3 sub-squares can be independently rotated and reflected into 8 different squares, from this single 9×9 composite square we can derive 89 = 134,217,728 essentially different 9×9 composite squares. Plenty more composite magic squares can also be derived if we select non-consecutive numbers in the magic sub-squares, like in Yang Hui's version of the 9×9 composite magic square. The next smallest composite magic squares of order 12, composed of magic squares of order 3 and 4 are given below.
For the base squares, there is only one essentially different 3rd order square, while there 880 essentially different 4th-order squares that we can choose from. Each pairing can produce two different composite squares. Since each magic sub-squares in each composite square can be expressed in 8 different forms due to rotations and reflections, there can be 1×880×89 + 880×1×816 ≈ 2.476×1017 essentially different 12×12 composite magic squares created this way, with consecutive numbers in each sub-square. In general, if there are cm and cn essentially different magic squares of order m and n, then we can form cm × cn × ( 8m2 + 8n2) composite squares of order mn, provided m ≠ n. If m = n, then we can form (cm)2 × 8m2 composite squares of order m2.
When the squares are of doubly even order, we can construct a composite magic square in a manner more elegant than the above process, in the sense that every magic subsquare will have the same magic constant. Let n be the order of the main square and m the order of the equal subsquares. The subsquares are filled one by one, in any order, with a continuous sequence of m2/2 smaller numbers (i.e. numbers less than or equal to n2/2) together with their complements to n2 + 1. Each subsquare as a whole will yield the same magic sum. The advantage of this type of composite square is that each subsquare is filled in the same way and their arrangement is arbitrary. Thus, the knowledge of a single construction of even order will suffice to fill the whole square. Furthermore, if the subsquares are filled in the natural sequence, then the resulting square will be pandiagonal. The magic sum of the subsquares is related to the magic sum of the whole square by where n = km.[24]
In the examples below, we have divided the order 12 square into nine subsquares of order 4 filled each with eight smaller numbers and, in the corresponding bishop's cells (two cells diagonally across, including wrap arounds, in the 4×4 subsquare), their complements to n2 + 1 = 145. Each subsquare is pandiagonal with magic constant 290; while the whole square on the left is also pandiagonal with magic constant 870.
In another example below, we have divided the order 12 square into four order 6 squares. Each of the order 6 squares are filled with eighteen small numbers and their complements using bordering technique given by al-Antaki. If we remove the shaded borders of the order 6 subsquares and form an order 8 square, then this order 8 square is again a magic square. In its full generality, we can take any m2/2 smaller numbers together with their complements to n2 + 1 to fill the subsquares, not necessarily in continuous sequence.
In this method a magic square is "multiplied" with a medjig square to create a larger magic square. The namesake of this method derives from mathematical game called medjig created by Willem Barink in 2006, although the method itself is much older.[citation needed] An early instance of a magic square constructed using this method occurs in Yang Hui's text for order 6 magic square.[citation needed] The LUX method to construct singly even magic squares is a special case of the medjig method, where only 3 out of 24 patterns are used to construct the medjig square.[citation needed]
The pieces of the medjig puzzle are 2×2 squares on which the numbers 0, 1, 2 and 3 are placed. There are three basic patterns by which the numbers 0, 1, 2 and 3 can be placed in a 2×2 square, where 0 is at the top left corner:
Each pattern can be reflected and rotated to obtain 8 equivalent patterns, giving us a total of 3×8 = 24 patterns. The aim of the puzzle is to take n2 medjig pieces and arrange them in an n × n medjig square in such a way that each row, column, along with the two long diagonals, formed by the medjig square sums to 3n, the magic constant of the medjig square. An n × n medjig square can create a 2n × 2n magic square where n > 2.
Given an n×n medjig square and an n×n magic square base, a magic square of order 2n×2n can be constructed as follows:
Assuming that we have an initial magic square base, the challenge lies in constructing a medjig square. For reference, the sums of each medjig piece along the rows, columns and diagonals, denoted in italics, are:
Doubly even squares: The smallest even ordered medjig square is of order 2 with magic constant 6. While it is possible to construct a 2×2 medjig square, we cannot construct a 4×4 magic square from it since 2×2 magic squares required to "multiply" it does not exist. Nevertheless, it is worth constructing these 2×2 medjig squares. The magic constant 6 can be partitioned into two parts in three ways as 6 = 5 + 1 = 4 + 2 = 3 + 3. There exist 96 such 2×2 medjig squares.[citation needed] In the examples below, each 2×2 medjig square is made by combining different orientations of a single medjig piece.
We can use the 2×2 medjig squares to construct larger even ordered medjig squares. One possible approach is to simply combine the 2×2 medjig squares together. Another possibility is to wrap a smaller medjig square core with a medjig border. The pieces of a 2×2 medjig square can form the corner pieces of the border. Yet another possibility is to append a row and a column to an odd ordered medjig square. An example of an 8×8 magic square is constructed below by combining four copies of the left most 2×2 medjig square given above:
The next example is constructed by bordering a 2×2 medjig square core.
Singly even squares: Medjig square of order 1 does not exist. As such, the smallest odd ordered medjig square is of order 3, with magic constant 9. There are only 7 ways of partitioning the integer 9, our magic constant, into three parts.[citation needed] If these three parts correspond to three of the medjig pieces in a row, column or diagonal, then the relevant partitions for us are:
A 3×3 medjig square can be constructed with some trial-and-error, as in the left most square below. Another approach is to add a row and a column to a 2×2 medjig square. In the middle square below, a left column and bottom row has been added, creating an L-shaped medjig border, to a 2×2 medjig square given previously. The right most square below is essentially same as the middle square, except that the row and column has been added in the middle to form a cross while the pieces of 2×2 medjig square are placed at the corners.
Once a 3×3 medjig square has been constructed, it can be converted into a 6×6 magic square. For example, using the left most 3×3 medjig square given above:
There are 1,740,800 such 3×3 medjig squares.[78] An easy approach to construct higher order odd medjig square is by wrapping a smaller odd ordered medjig square with a medjig border, just as with even ordered medjig squares. Another approach is to append a row and a column to an even ordered medjig square. Approaches such as the LUX method can also be used. In the example below, a 5×5 medjig square is created by wrapping a medjig border around a 3×3 medjig square given previously:
Solving partially completed magic squares is a popular mathematical pastime. The techniques needed are similar to those used in Sudoku or KenKen puzzles, and involve deducing the values of unfilled squares using logic and permutation group theory (Sudoku grids are not magic squares but are based on a related idea called Graeco-Latin squares).[67]
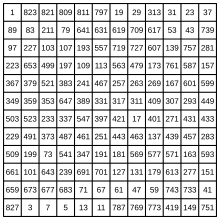
Certain extra restrictions can be imposed on magic squares.
If raising each number to the nth power yields another magic square, the result is a bimagic (n = 2), a trimagic (n = 3), or, in general, a multimagic square.
A magic square in which the number of letters in the name of each number in the square generates another magic square is called an alphamagic square.
There are magic squares consisting entirely of primes. Rudolf Ondrejka (1928–2001) discovered the following 3×3 magic square of primes, in this case nine Chen primes:
The Green–Tao theorem implies that there are arbitrarily large magic squares consisting of primes.
The following "reversible magic square" has a magic constant of 264 both upside down and right way up:[79]

When the extra constraint is to display some date, especially a birth date, then such magic squares are called birthday magic square. An early instance of such birthday magic square was created by Srinivasa Ramanujan. He created a 4×4 square in which he entered his date of birth in D–M–C-Y format in the top row and the magic happened with additions and subtractions of numbers in squares. Not only do the rows, columns, and diagonals add up to the same number, but the four corners, the four middle squares (17, 9, 24, 89), the first and last rows two middle numbers (12, 18, 86, 23), and the first and last columns two middle numbers (88, 10, 25, 16) all add up to the sum of 139.
Instead of adding the numbers in each row, column and diagonal, one can apply some other operation. For example, a multiplicative magic square has a constant product of numbers. A multiplicative magic square can be derived from an additive magic square by raising 2 (or any other integer) to the power of each element, because the logarithm of the product of 2 numbers is the sum of logarithm of each. Alternatively, if any 3 numbers in a line are 2a, 2b and 2c, their product is 2a+b+c, which is constant if a+b+c is constant, as they would be if a, b and c were taken from ordinary (additive) magic square.[80] For example, the original Lo-Shu magic square becomes:
Other examples of multiplicative magic squares include:
Still using Ali Skalli's non iterative method, it is possible to produce an infinity of multiplicative magic squares of complex numbers[81] belonging to set. On the example below, the real and imaginary parts are integer numbers, but they can also belong to the entire set of real numbers . The product is: −352,507,340,640 − 400,599,719,520 i.
Additive-multiplicative magic squares and semimagic squares satisfy properties of both ordinary and multiplicative magic squares and semimagic squares, respectively.[82]
It is unknown if any additive-multiplicative magic squares smaller than 7×7 exist, but it has been proven that no 3×3 or 4×4 additive-multiplicative magic squares and no 3×3 additive-multiplicative semimagic squares exist.[83]

Magic squares may be constructed which contain geometric shapes instead of numbers. Such squares, known as geometric magic squares, were invented and named by Lee Sallows in 2001.[84]
In the example shown the shapes appearing are two dimensional. It was Sallows' discovery that all magic squares are geometric, the numbers that appear in numerical magic squares can be interpreted as a shorthand notation which indicates the lengths of straight line segments that are the geometric 'shapes' occurring in the square. That is, numerical magic squares are that special case of a geometric magic square using one dimensional shapes.[85]

In 2017, following initial ideas of William Walkington and Inder Taneja, the first linear area magic square (L-AMS) was constructed by Walter Trump.[86]
Other two dimensional shapes than squares can be considered. The general case is to consider a design with N parts to be magic if the N parts are labeled with the numbers 1 through N and a number of identical sub-designs give the same sum. Examples include magic circles, magic rectangles, magic triangles[87] magic stars, magic hexagons, magic diamonds. Going up in dimension results in magic spheres, magic cylinders, magic cubes, magic parallelepiped, magic solids, and other magic hypercubes.
Possible magic shapes are constrained by the number of equal-sized, equal-sum subsets of the chosen set of labels. For example, if one proposes to form a magic shape labeling the parts with {1, 2, 3, 4}, the sub-designs will have to be labeled with {1,4} and {2,3}.[87]

In 1992, Demirörs, Rafraf, and Tanik published a method for converting some magic squares into n-queens solutions, and vice versa.[89]
Magic squares of order 3 through 9, assigned to the seven planets, and described as means to attract the influence of planets and their angels (or demons) during magical practices, can be found in several manuscripts all around Europe starting at least since the 15th century. Among the best known, the Liber de Angelis, a magical handbook written around 1440, is included in Cambridge Univ. Lib. MS Dd.xi.45.[90] The text of the Liber de Angelis is very close to that of De septem quadraturis planetarum seu quadrati magici, another handbook of planetary image magic contained in the Codex 793 of the Biblioteka Jagiellońska (Ms BJ 793).[91] The magical operations involve engraving the appropriate square on a plate made with the metal assigned to the corresponding planet,[92] as well as performing a variety of rituals. For instance, the 3×3 square, that belongs to Saturn, has to be inscribed on a lead plate. It will, in particular, help women during a difficult childbirth.
In about 1510 Heinrich Cornelius Agrippa wrote De Occulta Philosophia, drawing on the Hermetic and magical works of Marsilio Ficino and Pico della Mirandola. In its 1531 edition, he expounded on the magical virtues of the seven magical squares of orders 3 to 9, each associated with one of the astrological planets, much in the same way as the older texts did. This book was very influential throughout Europe until the Counter-Reformation, and Agrippa's magic squares, sometimes called kameas, continue to be used within modern ceremonial magic in much the same way as he first prescribed.[93]

The most common use for these kameas is to provide a pattern upon which to construct the sigils of spirits, angels or demons; the letters of the entity's name are converted into numbers, and lines are traced through the pattern that these successive numbers make on the kamea. In a magical context, the term magic square is also applied to a variety of word squares or number squares found in magical grimoires, including some that do not follow any obvious pattern, and even those with differing numbers of rows and columns. They are generally intended for use as talismans. For instance the following squares are: The Sator square, one of the most famous magic squares found in a number of grimoires including the Key of Solomon; a square "to overcome envy", from The Book of Power;[94] and two squares from The Book of the Sacred Magic of Abramelin the Mage, the first to cause the illusion of a superb palace to appear, and the second to be worn on the head of a child during an angelic invocation:

A magic square in a musical composition is not a block of numbers – it is a generating principle, to be learned and known intimately, perceived inwardly as a multi-dimensional projection into that vast (chaotic!) area of the internal ear – the space/time crucible – where music is conceived. ... Projected onto the page, a magic square is a dead, black conglomeration of digits; tune in, and one hears a powerful, orbiting dynamo of musical images, glowing with numen and lumen.[98]
Isomura Kittoku.
Isomura Kittoku.
Isomura Kittoku.
Isomura Kittoku.
Some 'near misses' have been found such as the Parker Square [2]
The two corresponding prizes are still to be won!
The Parker Square is a mascot for people who give it a go but ultimately fall short.
Moreover, it's a magic square, a pattern in which God supposedly instructed the early Hebrews to gain power from names or their numeric equivalents.
I love when they bring the nerdy FBI guy in to explain the concept of "the magic square", which he does by telling us that magic squares have been around for a while, and then nothing else. Unless I missed something, all I have at this point is that magic squares are squares that people once thought were magic.