Simetría
La simetría (del griego őύν "con" y μέτροv "medida") es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios.
Cuando hablamos de objetos físicos o elementos geométricos el concepto de simetría está asociado a transformaciones geométricas tales como las rotaciones, las reflexiones o las traslaciones.
[3] El conjunto de operaciones que preservan una propiedad dada del objeto forman un grupo.
Los ejemplos incluyen funciones pares e impares en cálculo, grupos simétricos en álgebra abstracta, matrices simétricas en álgebra lineal,[4] y grupos de Galois en la teoría de Galois.
[8] La arquitectura modernista, comenzando con el estilo internacional, se basa en cambio en «alas y equilibrio de masas».
Los indios navajos estadounidenses usaban diagonales en negrita y motivos rectangulares.
Muchas alfombras orientales tienen intrincados centros y bordes reflejados que traducen un patrón.
No es sorprendente que las alfombras rectangulares tengan típicamente las simetrías de un rectángulo, es decir, motivos que se reflejan tanto en el eje horizontal como en el vertical.
Los ejemplos incluyen abalorios, muebles, pinturas de arena, nudos, máscaras e instrumentos musicales.
[14] Al crear un logotipo en una cuadrícula y utilizar la teoría de la simetría, los diseñadores pueden organizar su trabajo, crear un diseño simétrico o asimétrico, determinar el espacio entre letras, determinar cuánto espacio negativo se requiere en el diseño y cómo acentuar partes del logo para que se destaque.
Los seres humanos encuentran la simetría bilateral en los rostros físicamente atractivos;[15] indica salud y aptitud genética.
La gente prefiere formas que tengan algo de simetría, pero con la complejidad suficiente para hacerlas interesantes.
[19] En física el concepto de simetría puede formularse en una forma no geométrica.
En ese caso K representaría el conjunto de lagrangianos admisibles, k0 el lagrangiano del sistema bajo estudio y G puede representar traslaciones espaciales (conservación del momento lineal), traslaciones temporales (conservación de la energía), rotaciones (conservación del momento angular) u otro tipo de simetrías abstractas (conservación de la carga eléctrica, el número leptónico, la paridad, etc.) Estos dos ejemplos anteriores son casos del teorema de Noether, un resultado general que establece que si existe un grupo uniparamétrico de simetría G para el lagrangiano tal que:
La simetría es importante para la química (en particular en la química orgánica) porque sustenta esencialmente todas las interacciones específicas entre moléculas en la naturaleza (es decir, a través de la interacción de moléculas quirales naturales y artificiales con sistemas biológicos inherentemente quirales).
Una pequeña minoría no presenta ningún tipo de simetría (son asimétricos).
Sobre este eje, se establecen planos principales de simetría; dos perpendiculares que definen las posiciones per-radiales.
Las estructuras en otros planos (bisectrices de los per-radiales) quedan en posiciones inter-radiales.
La zona entre los per-radiales y los inter-radiales es la zona ad-radial La mayoría de especies animales tiene simetría bilateral y pertenece por tanto al grupo Bilateria, aunque hay especies como los erizos y las estrellas de mar, que presentan simetría radial secundaria (las fases de desarrollo tempranas y las larvas poseen simetría bilateral que posteriormente se pierde en el adulto).
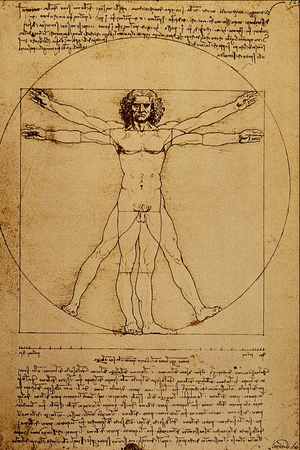
La simetría bilateral permite la definición de un eje corporal en la dirección del movimiento, lo que favorece la formación de un sistema nervioso centralizado y la cefalización... Para un observador humano, algunos tipos de simetría son más sobresalientes que otros, en particular el más sobresaliente es un reflejo con un eje vertical, como el presente en el rostro humano.
Tanto los estudios conductuales como los neurofisiológicos han confirmado la sensibilidad especial a la simetría de reflexión en humanos y también en otros animales.
El papel de la simetría en la agrupación y la organización figura / suelo ha sido confirmado en muchos estudios.
Las regiones extraestriadas incluyeron V3A, V4, V7 y el complejo occipital lateral (LOC).
Los estudios electrofisiológicos han encontrado una negatividad posterior tardía que se origina en las mismas áreas.
[27] En general, una gran parte del sistema visual parece estar involucrado en el procesamiento de la simetría visual, y estas áreas involucran redes similares a las responsables de detectar y reconocer objetos.
La simetría también es una consideración importante en la formación de escalas y acordes, ya que la música tradicional o tonal está formada por grupos de tonos no simétricos, como la escala diatónica o el acorde mayor.
[29] Los ciclos de intervalo son simétricos y, por lo tanto, no diatónicos.
Las progresiones tonales cíclicas en las obras de compositores románticos como Gustav Mahler y Richard Wagner forman un vínculo con las sucesiones tonales cíclicas en la música atonal de modernistas como Bartók, Alexander Scriabin, Edgard Varèse y la escuela de Viena.
Al mismo tiempo, estas progresiones señalan el final de la tonalidad.
[29][30] La primera composición extendida basada consistentemente en relaciones tonales simétricas fue probablemente el Cuarteto de Alban Berg, op.