Pirámide (geometría)
[5] Se llama pirámide a un cuerpo geométrico que es la unión de todos los segmentos que unen todos los puntos de un polígono S con un punto P exterior al plano del polígono.[6] Se considera que el polígono es una parte del plano y es un conjunto bidimensional.Si la base de una pirámide oblicua es un polígono regular, es posible que no todas sus caras laterales son triángulos isósceles.Sus caras laterales son todas triángulos isósceles idénticos cuya altura corresponde al apotema de la pirámide.Se le asigna un símbolo de Schläfli extendido ( ) ∨ {n}, que representa un punto, ( ), unido (desplazado ortogonalmente) a un polígono regular, {n}.Las pirámides cuadradas y pentagonales también pueden estar compuestas por polígonos regulares convexos, en cuyo caso son sólidos de Johnson.Las pirámides de base hexagonal o superior deben estar compuestas por triángulos isósceles.Una pirámide hexagonal con triángulos equiláteros sería una figura completamente plana, y en una heptagonal o superior la apotema de los triángulos no tiene la longitud necesaria para poder unirse al vértice.[9] Por ejemplo, la pirámide pentagrámica tiene por base una estrella pentagonal y 5 lados triangulares que se cruzan entre sí.Una pirámide recta se puede describir mediante la notación como ( )∨P, donde ( ) representa el ápice, ∨ es el operador unión y P es el polígono base.Un tetraedro recto sobre un triángulo isósceles se puede anotar de otras tres formas: como ( )∨[( )∨{ }], que describe la unión del punto con los vértices de una base con forma de triángulo isósceles compuesta por otro punto y un segmento; como [( )∨( )]∨{ }, que describe la unión de dos puntos que a su vez se unen con un segmento; o como { }∨{ }, que describe la unión de dos segmentos ortogonales entre sí (un disfenoide digonal con cuatro caras isósceles).Para calcular la longitud de la apotema se aplica la trigonometría.Ahora, reemplazando el valor de la apotema a en el área del polígono regular (Ab) tenemos:El matemático y astrónomo indio Aryabhata dedujo la fórmula utilizando un método similar, que aparece en su obra titulada Aryabhatiya (sección 2.6), que data del año 499 a. C. El volumen de una pirámide cuya base es un polígono regular puede calcularse a partir del lado del polígono regular que define su base y de la altura de la pirámide.Esta fórmula solo se aplica para n = 2, 3, 4 y 5; y también cubre el caso n = 6, para el que el volumen es igual a cero (es decir, la altura de la pirámide es cero).El centroide o baricentro de un tetraedro regular está situado en su altura.La tabla contiene fórmulas para las propiedades geométricas de una pirámide recta regular general en la columna 2, y en las columnas 3 y 4 específicamente para los casosPara obtener este resultado, se parte del límite conocidoDada una pirámide recta de altura h, la pirámide homotética cuyo volumen es la mitad tendrá una altura h': Un plano paralelo a la base, situado a dicha distancia de la cúspide, cortará a la pirámide en dos partes de igual volumen.Se puede usar una sucesión de pirámides regulares que tienen un polígono regular como base con cada vez más lados para aproximar un cono, que por definición tiene una circunferencia como base.Si la base de la pirámide es un polígono regular conlados, el sucesión que tiende alinfinitose aproxima al perímetro de una circunferencia.El cono circular puede entenderse como una pirámide regular, por así decirlo, donde la base tiene un número infinito de vértices y la longitud del lado tiene el límite 0.Esto permite deducir el volumen del cono de la manera que se explica a continuación.Usando la fórmula del área de un polígono regular con: Para determinar el volumen de un cono, se puede calcular el límite cuando: Una pirámide bidimensional es un triángulo, formado por un borde base conectado a un punto no colineal llamado ápice.La familia de símplices incluye pirámides en cualquier dimensión, aumentando a espacios de mayor orden para formar sucesivamente triángulos, tetraedros, pentacorones, 5-símplex, etc. Un símplex n-dimensional tiene como mínimo n+1 vértices, con todos los pares de vértices conectados por aristas, todas las ternas de vértices que definen caras, todos los grupos de cuatro puntos que definen celdas tetraédricas, y así sucesivamente.Un poliedro con v vértices, e aristas y f caras puede ser la base de una pirámide poliédrica con v+1 vértices, e+v aristas, f+e caras y 1+f celdas.Una "pirámide poliédrica" 4D con simetría axial se puede visualizar en 3D con un diagrama de Schlegel, una proyección 3D que coloca el vértice en el centro del poliedro base.



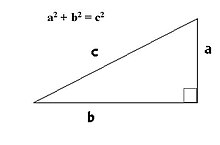
Altura de la pirámide: h = a .
Apotema de la base: a b = b .
Apotema de la pirámide: a p = c





Colo rojo: cono con la misma propiedad y la misma superficie
:






