Cero
Es el signo numérico de valor nulo, que en notación posicional ocupa los lugares donde no hay una cifra significativa.
[2] La palabra «cero» llega al castellano desde el italiano zero, y esta del bajo latín zephyrum;[3] esta palabra proviene de la traducción del nombre sánscrito shunya (vacío) al árabe ṣifr (صفر).
Cabe señalar que la palabra italiana zefiro ya existía previamente, pero con el significado de "viento del oeste", y provenía (como ya mencionamos) del bajo latín, que a su vez lo tomó del griego zephyrus; esta última palabra pudo haber influido en la ortografía utilizada al transcribir el vocablo árabe ṣifr al italiano.
Para la simple noción de carencia, se utilizan a menudo las palabras "nada" y "ninguno".
Las palabras de argot en inglés para cero incluyen "zip", "zilch", "nada" y "scratch".
El cero apareció por primera vez en Babilonia en el siglo III a. C., aunque su escritura en tablillas de arcilla se remonta al 2000 a. C. Los babilonios escribían en arcilla sin cocer, sobre superficies planas o tablillas.
Alrededor del 400 a. C., los babilonios comenzaron a colocar el signo de «dos cuñas» en los lugares donde en nuestro sistema escribiríamos un cero, que se leía «varios».
En otras tablillas usaron un solo «gancho» y, en algunos casos, la deformación de este se asemeja a la forma del cero.
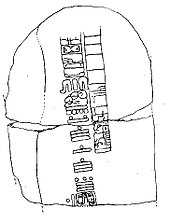
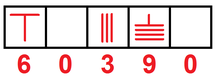
El cero también surgió en Mesoamérica e ideado por las civilizaciones mesoamericanas antes de la era cristiana, por la cultura maya.
Ptolomeo solía utilizar el símbolo entre dígitos o al final del número.
Sus números eran letras de su alfabeto; para representar cifras usaban: I, V, X, L, C, D, M, agrupándolas.
El Sun Zi Suanjing, de fecha desconocida pero que se estima que data del siglo I al V d. C., y los registros japoneses que datan del siglo XVIII, describen cómo el sistema de barras de conteo chino del siglo IV a. C. permitía realizar cálculos decimales.
[8] Según A History of Mathematics, las barras "dieron la representación decimal de un número, con un espacio vacío que indica cero".
[11] Los árabes lo transmitieron por el Magreb y Al-Ándalus, pasando posteriormente al resto de Europa.
Los primeros manuscritos que muestran las cifras indias (llamadas entonces «árabes») provienen del norte de España y son del siglo X: el Codex Vigilanus y el Codex Aemilianensis.
Desde el siglo XX, y especialmente con el desarrollo de la informática, es frecuente que este signo aparezca cortado por una barra diagonal (/), nueva notación que evitaba la confusión con la grafía de la letra «o».
En los números reales (incluso en los complejos) la división entre cero es una indeterminación; así, las expresiones: carecen de sentido.
Por ejemplo: Sin embargo, si se analiza cada numerador y denominador por separado, el límite de todo ellos es cero.
Por eso se dice que 0⁄0 es indeterminado, pues pueden obtenerse resultados tan diferentes como infinito, uno o cero.
no está definido como potencia, pero según el contexto o por comodidad se puede elegir uno de los resultados mediante una definición.
En general se le dice cero al elemento neutro de un grupo abeliano.
Al medir la intensidad del sonido en decibelioss o fonios, el nivel cero se fija arbitrariamente en un valor de referencia, por ejemplo, en el valor del umbral de audición.