Cinta de Moebius

Superficie no orientable con un borde

Una tira de Möbius hecha con papel y cinta adhesiva.

En matemáticas , una tira de Möbius , una banda de Möbius o un bucle de Möbius ^[a] es una superficie que se puede formar uniendo los extremos de una tira de papel con una media torsión. Como objeto matemático, fue descubierto por Johann Benedict Listing y August Ferdinand Möbius en 1858, pero ya había aparecido en mosaicos romanos del siglo III d.C. La banda de Möbius es una superficie no orientable , lo que significa que dentro de ella no se pueden distinguir consistentemente los giros en el sentido de las agujas del reloj y en el sentido contrario a las agujas del reloj. Cada superficie no orientable contiene una tira de Möbius.

Como espacio topológico abstracto, la franja de Möbius se puede incrustar en el espacio euclidiano tridimensional de muchas maneras diferentes: un medio giro en el sentido de las agujas del reloj es diferente de un medio giro en el sentido contrario a las agujas del reloj, y también se puede incrustar con un número impar de giros mayor que uno, o con una línea central anudada . Dos incrustaciones cualesquiera con el mismo nudo para la línea central y el mismo número y dirección de giros son topológicamente equivalentes . Todas estas incrustaciones tienen un solo lado, pero cuando se incrustan en otros espacios, la tira de Möbius puede tener dos lados. Tiene una sola curva límite .

Varias construcciones geométricas de la banda de Möbius le confieren una estructura adicional. Puede ser barrida como una superficie reglada por un segmento de línea que gira en un plano giratorio, con o sin autocruces. Una tira de papel delgada con sus extremos unidos para formar una tira de Möbius puede doblarse suavemente como una superficie desarrollable o plegarse hasta quedar plana ; las tiras de Möbius aplanadas incluyen el trihexaflexágono . La franja de Möbius sudanesa es una superficie mínima en una hiperesfera , y la franja de Meeks Möbius es una superficie mínima que se intersecta a sí misma en el espacio euclidiano ordinario. Tanto la franja de Möbius sudanesa como otra franja de Möbius que se cruza a sí misma, la cross-cap, tienen un límite circular. Una franja de Möbius sin su límite, llamada franja de Möbius abierta, puede formar superficies de curvatura constante . Ciertos espacios altamente simétricos cuyos puntos representan líneas en el plano tienen la forma de una cinta de Möbius.

Las muchas aplicaciones de las tiras de Möbius incluyen correas mecánicas que se desgastan uniformemente en ambos lados, montañas rusas de doble vía cuyos vagones se alternan entre las dos vías y mapas mundiales impresos de manera que las antípodas aparecen una frente a la otra. Las tiras de Möbius aparecen en moléculas y dispositivos con nuevas propiedades eléctricas y electromecánicas y se han utilizado para demostrar resultados de imposibilidad en la teoría de la elección social . En la cultura popular, las tiras de Möbius aparecen en obras de arte de MC Escher , Max Bill y otros, y en el diseño del símbolo del reciclaje . Muchos conceptos arquitectónicos se han inspirado en la franja de Möbius, incluido el diseño del edificio del Salón de la Fama de NASCAR . Artistas como Harry Blackstone Sr. y Thomas Nelson Downs han basado sus trucos de magia escénica en las propiedades de la tira de Möbius. Los cánones de JS Bach han sido analizados mediante cintas de Möbius. Muchas obras de ficción especulativa presentan tiras de Möbius; En términos más generales, una estructura argumental basada en la tira de Möbius, de acontecimientos que se repiten con un giro, es común en la ficción.

Historia

El descubrimiento de la tira de Möbius como objeto matemático se atribuye de forma independiente a los matemáticos alemanes Johann Benedict Listing y August Ferdinand Möbius en 1858. ^[2] Sin embargo, ya se conocía mucho antes, tanto como objeto físico como en representaciones artísticas; en particular, se puede ver en varios mosaicos romanos del siglo III d.C. ^{[3] [4]} En muchos casos estos simplemente representan cintas enrolladas como límites. Cuando el número de bobinas es impar, estas cintas son tiras de Möbius, pero para un número par de bobinas son topológicamente equivalentes a anillos sin torcer . Por lo tanto, si la cinta es una tira de Möbius puede ser una coincidencia, más que una elección deliberada. En al menos un caso, una cinta con diferentes colores en diferentes lados se dibujó con un número impar de vueltas, lo que obligó a su artista a hacer un arreglo torpe en el punto donde los colores no coincidían. ^[3] Otro mosaico de la ciudad de Sentinum (representado) muestra el zodíaco , sostenido por el dios Aion , como una banda con un solo giro. No hay evidencia clara de que la unilateralidad de esta representación visual del tiempo celestial fuera intencional; podría haberse elegido simplemente como una forma de hacer que todos los signos del zodíaco aparezcan en el lado visible de la tira. También se supone que algunas otras representaciones antiguas de los ourobouros o de decoraciones en forma de ocho representan tiras de Möbius, pero no está claro si estaban destinadas a representar tiras planas de algún tipo. ^[4]

Independientemente de la tradición matemática, los maquinistas saben desde hace mucho tiempo que las correas mecánicas se desgastan la mitad de rápido cuando se forman bandas de Möbius, porque utilizan toda la superficie de la correa y no sólo la superficie interior de una correa sin torcer. ^[3] Además, un cinturón de este tipo puede ser menos propenso a curvarse de un lado a otro. Una de las primeras descripciones escritas de esta técnica data de 1871, posterior a las primeras publicaciones matemáticas sobre la cinta de Möbius. Mucho antes, una imagen de una bomba de cadena en una obra de Ismail al-Jazari de 1206 muestra una configuración de tira de Möbius para su cadena de transmisión. ^[4] Otro uso de esta superficie fue hecho por costureras en París (en una fecha no especificada): iniciaron a los novatos exigiéndoles que cosieran una tira de Möbius a modo de cuello en una prenda. ^[3]

Propiedades

Un objeto 2D que recorre una vez la cinta de Möbius regresa en forma reflejada

La cinta de Möbius tiene varias propiedades curiosas. Es una superficie no orientable : si un objeto bidimensional asimétrico se desliza una vez alrededor de la franja, regresa a su posición inicial como su imagen especular. En particular, una flecha curva que apunta en el sentido de las agujas del reloj (↻) volvería a ser una flecha que apunta en el sentido contrario a las agujas del reloj (↺), lo que implica que, dentro de la banda de Möbius, es imposible definir consistentemente lo que significa estar en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj. Es la superficie no orientable más simple: cualquier otra superficie es no orientable si y sólo si tiene una tira de Möbius como subconjunto . ^[5] De manera relacionada, cuando se incrusta en el espacio euclidiano , la tira de Möbius tiene un solo lado. Un objeto tridimensional que se desliza una vez alrededor de la superficie de la tira no se refleja, sino que regresa al mismo punto de la tira en lo que localmente parece ser su otro lado, lo que demuestra que ambas posiciones son realmente parte de un solo lado. . Este comportamiento es diferente de las superficies orientables familiares en tres dimensiones, como las modeladas con hojas de papel planas, pajitas cilíndricas o bolas huecas, en las que un lado de la superficie no está conectado con el otro. ^[6] Sin embargo, esto es una propiedad de su incrustación en el espacio más que una propiedad intrínseca de la propia banda de Möbius: existen otros espacios topológicos en los que la banda de Möbius puede incrustarse de modo que tenga dos lados. ^[7] Por ejemplo, si las caras frontal y posterior de un cubo se pegan entre sí con un reflejo especular de izquierda a derecha, el resultado es un espacio topológico tridimensional (el producto cartesiano de una tira de Möbius con un intervalo) en que las mitades superior e inferior del cubo se pueden separar entre sí mediante una tira de Möbius de dos caras. ^[b] A diferencia de los discos, esferas y cilindros, para los cuales es posible incrustar simultáneamente un conjunto incontable de copias disjuntas en un espacio tridimensional, sólo se puede incrustar simultáneamente un número contable de tiras de Möbius. ^{[9] [10] [11]}

Un camino a lo largo del borde de una franja de Möbius, trazado hasta regresar a su punto inicial en el borde, incluye todos los puntos límite de la franja de Möbius en una única curva continua. Para una tira de Möbius formada pegando y girando un rectángulo, tiene el doble de longitud que la línea central de la tira. En este sentido, la tira de Möbius se diferencia de un anillo no retorcido y de un disco circular en que tiene un solo límite. ^[6] Una tira de Möbius en el espacio euclidiano no se puede mover ni estirar hasta alcanzar su imagen especular; es un objeto quiral con diestro o zurdo. ^[12] Las tiras de Möbius con un número impar de medias vueltas mayores que uno, o que están anudadas antes de pegarlas, se distinguen como subconjuntos incrustados del espacio tridimensional, aunque todas son equivalentes como superficies topológicas bidimensionales. ^[13] Más precisamente, dos tiras de Möbius están incrustadas de manera equivalente en un espacio tridimensional cuando sus líneas centrales determinan el mismo nudo y tienen el mismo número de vueltas entre sí . ^[14] Sin embargo, con un número par de giros, se obtiene una superficie topológica diferente, llamada anillo . ^[15]

La tira de Möbius se puede transformar continuamente en su línea central, haciéndola más estrecha mientras se fijan los puntos en la línea central. Esta transformación es un ejemplo de retracción por deformación , y su existencia significa que la franja de Möbius tiene muchas de las mismas propiedades que su línea central, que topológicamente es un círculo. En particular, su grupo fundamental es el mismo que el grupo fundamental de un círculo, un grupo cíclico infinito . Por lo tanto, los caminos en la franja de Möbius que comienzan y terminan en el mismo punto se pueden distinguir topológicamente (hasta la homotopía ) sólo por el número de veces que dan vueltas alrededor de la franja. ^[dieciséis]

Cortar una tira de Möbius a lo largo de la línea central con un par de tijeras produce una tira larga con cuatro medias vueltas (en relación con un anillo o cilindro sin torcer) en lugar de dos tiras separadas. Dos de las medias vueltas se deben al hecho de que esta tira más delgada pasa dos veces por la media vuelta de la tira de Möbius original, y las otras dos provienen de la forma en que las dos mitades de la tira más delgada se envuelven entre sí. El resultado no es una cinta de Möbius, sino que topológicamente equivale a un cilindro. Cortar de nuevo esta tira de doble torsión a lo largo de su línea central produce dos tiras unidas de doble torsión. Si, en cambio, se corta una tira de Möbius a lo largo, un tercio de su ancho, se obtienen dos tiras unidas. Uno de los dos es una tira de Möbius central, más delgada, mientras que el otro tiene dos medias vueltas. ^[6] Estas formas interconectadas, formadas por cortes longitudinales de tiras de Möbius con diferentes anchos, a veces se denominan anillos paradrómicos . ^{[17] [18]}

La franja de Möbius se puede cortar en seis regiones mutuamente adyacentes, lo que demuestra que los mapas en la superficie de la franja de Möbius a veces pueden requerir seis colores, en contraste con el teorema de los cuatro colores para el plano. ^[19] Seis colores siempre son suficientes. Este resultado es parte del teorema de Ringel-Youngs , que establece cuántos colores necesita cada superficie topológica. ^[20] Los bordes y vértices de estas seis regiones forman el gráfico de Tietze , que es un gráfico dual en esta superficie para el gráfico completo de seis vértices , pero no se puede dibujar sin cruces en un plano . Otra familia de gráficos que se pueden incrustar en la franja de Möbius, pero no en el plano, son las escaleras de Möbius , los límites de las subdivisiones de la franja de Möbius en rectángulos que se encuentran de un extremo a otro. ^[21] Estos incluyen el gráfico de utilidad, un gráfico bipartito completo de seis vértices cuya incrustación en la tira de Möbius muestra que, a diferencia del plano, el problema de las tres utilidades se puede resolver en una tira de Möbius transparente. ^[22] La característica de Euler de la franja de Möbius es cero , lo que significa que para cualquier subdivisión de la franja por vértices y aristas en regiones, los números , y de vértices, aristas y regiones satisfacen . Por ejemplo, el gráfico de Tietze tiene vértices, aristas y regiones; . ^[19] ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle V-E+F=0}$ ${\displaystyle 12}$ ${\displaystyle 18}$ ${\displaystyle 6}$ ${\displaystyle 12-18+6=0}$

Construcciones

Hay muchas formas diferentes de definir superficies geométricas con la topología de la banda de Möbius, generando realizaciones con propiedades geométricas adicionales.

Barrer un segmento de línea

Una forma de incrustar la tira de Möbius en el espacio euclidiano tridimensional es barrerla mediante un segmento de línea que gira en un plano, que a su vez gira alrededor de una de sus líneas. ^[23] Para que la superficie barrida se encuentre consigo misma después de un medio giro, el segmento de línea debe girar alrededor de su centro a la mitad de la velocidad angular de la rotación del avión. Esto puede describirse como una superficie paramétrica definida por ecuaciones para las coordenadas cartesianas de sus puntos,

$${\displaystyle {\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u\\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v)&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{aligned}}}$$

,. ^[24]toro sólidoconectado. ^[25] ${\displaystyle 0\leq u<2\pi }$ ${\displaystyle -1\leq v\leq 1}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle xy}$ ${\displaystyle (0,0,0)}$

Una línea o segmento de línea barrido con un movimiento diferente, que gira en un plano horizontal alrededor del origen a medida que se mueve hacia arriba y hacia abajo, forma el conoide o cilindroide de Plücker , una superficie reglada algebraica en forma de una tira de Möbius que se cruza sola . ^[26] Tiene aplicaciones en el diseño de engranajes . ^[27]

Superficies poliédricas y pliegues planos.

Trihexaflexagon en flexión

Una tira de papel puede formar una tira de Möbius aplanada en el plano doblándola en ángulos de modo que su línea central quede a lo largo de un triángulo equilátero y uniendo los extremos. La tira más corta posible para esto consta de tres triángulos equiláteros, doblados en los bordes donde se unen dos triángulos. Su relación de aspecto  (la relación entre la longitud de la tira ^[c] y su ancho) es , y el mismo método de plegado funciona para cualquier relación de aspecto mayor. ^{[28] [29]} Para una franja de nueve triángulos equiláteros, el resultado es un trihexaflexágono , que se puede flexionar para revelar diferentes partes de su superficie. ^[30] Para tiras demasiado cortas para aplicar este método directamente, primero se puede "doblar en acordeón" la tira en su dirección ancha hacia adelante y hacia atrás usando un número par de pliegues. Con dos pliegues, por ejemplo, una tira se convertiría en una tira plegada cuya sección transversal tiene forma de 'N' y seguiría siendo una 'N' después de media torsión. La tira más estrecha doblada en acordeón se puede doblar y unir de la misma manera que lo haría una tira más larga. ^{[28] [29]} ${\displaystyle 60^{\circ }}$ ${\displaystyle {\sqrt {3}}\approx 1.73}$ ${\displaystyle 1\times 1}$ ${\displaystyle 1\times {\tfrac {1}{3}}}$

Tiras de Möbius poliédricas de cinco vértices y plegadas planas

La tira de Möbius también puede incrustarse como una superficie poliédrica en el espacio o plegarse en el plano, con sólo cinco caras triangulares compartiendo cinco vértices. En este sentido, es más simple que el cilindro , que requiere seis triángulos y seis vértices, incluso cuando se representa de manera más abstracta como un complejo simplicial . ^{[31] [d]} Una tira de Möbius de cinco triángulos se puede representar de forma más simétrica mediante cinco de los diez triángulos equiláteros de un simplex regular de cuatro dimensiones . Esta tira de Möbius poliédrica de cuatro dimensiones es la única tira de Möbius apretada , una que es completamente de cuatro dimensiones y para la cual todos los cortes por hiperplanos la separan en dos partes que son topológicamente equivalentes a discos o círculos. ^[32]

Otras incrustaciones poliédricas de tiras de Möbius incluyen una con cuatro cuadriláteros convexos como caras, otra con tres caras de cuadrilátero no convexas ^[33] y una que utiliza los vértices y el punto central de un octaedro regular , con un límite triangular. ^[34] Cada triangulación abstracta del plano proyectivo se puede incrustar en 3D como una tira poliédrica de Möbius con un límite triangular después de eliminar una de sus caras; ^[35] un ejemplo es el plano proyectivo de seis vértices obtenido añadiendo un vértice a la tira de Möbius de cinco vértices, conectado por triángulos a cada uno de sus bordes límite. ^[31] Sin embargo, no todas las triangulaciones abstractas de la banda de Möbius pueden representarse geométricamente, como una superficie poliédrica. ^[36] Para que sea realizable, es necesario y suficiente que no haya dos ciclos de 3 no contráctiles y disjuntos en la triangulación. ^[37]

Rectángulos suavemente incrustados

Una tira de Möbius rectangular, hecha uniendo los extremos de un rectángulo de papel, se puede incrustar suavemente en un espacio tridimensional siempre que su relación de aspecto sea mayor que , la misma relación que para la versión de triángulo equilátero plegado plano de la tira de Möbius. ^[38] Esta incrustación triangular plana puede elevarse a una incrustación suave ^[e] en tres dimensiones, en la que la tira queda plana en tres planos paralelos entre tres rodillos cilíndricos, cada uno de ellos tangente a dos de los planos. ^[38] Matemáticamente, una hoja de papel incrustada suavemente se puede modelar como una superficie desarrollable , que puede doblarse pero no estirarse. ^{[39] [40]} A medida que su relación de aspecto disminuye hacia , todas las incrustaciones suaves parecen acercarse a la misma forma triangular. ^[41] ${\displaystyle {\sqrt {3}}\approx 1.73}$ ${\displaystyle {\sqrt {3}}}$

Los pliegues longitudinales de una tira de Möbius plana doblada en acordeón evitan que se forme una incrustación tridimensional en la que las capas se separan entre sí y se doblan suavemente sin arrugarse ni estirarse fuera de los pliegues. ^[29] En cambio, a diferencia del caso plegado plano, hay un límite inferior para la relación de aspecto de las tiras de Möbius rectangulares lisas. Su relación de aspecto no puede ser inferior a , incluso si se permiten las autointersecciones. Existen tiras de Möbius suaves que se intersecan solas para cualquier relación de aspecto por encima de este límite. ^{[29] [42]} Sin autointersecciones, la relación de aspecto debe ser al menos ^[43] ${\displaystyle \pi /2\approx 1.57}$

$${\displaystyle {\frac {2}{3}}{\sqrt {3+2{\sqrt {3}}}}\approx 1.695.}$$

Problema no resuelto en matemáticas :

¿Se puede pegar un rectángulo de papel de extremo a extremo para formar una tira de Möbius suave incrustada en el espacio? ^[F] ${\displaystyle 12\times 7}$

(más problemas sin resolver en matemáticas)

Para las relaciones de aspecto entre este límite y , ha sido un problema abierto si ${\displaystyle {\sqrt {3}}}$existen incrustaciones suaves, sin autointersección . ^{[29] [42] [43]} En 2023, Richard Schwartz anunció una prueba de que no existen, pero este resultado aún espera revisión por pares y publicación. ^{[44] [45]} Si el requisito de suavidad se relaja para permitir superficies continuamente diferenciables , el teorema de Nash-Kuiper implica que dos bordes opuestos cualesquiera de cualquier rectángulo se pueden pegar para formar una tira de Möbius incrustada, sin importar cuán pequeña sea la relación de aspecto. se convierte. ^[g] El caso límite, una superficie obtenida a partir de una franja infinita del plano entre dos líneas paralelas, pegadas con orientación opuesta entre sí, se llama franja de Möbius ilimitada o haz de líneas tautológicas reales . ^[46] Aunque no tiene una incrustación cerrada y suave en el espacio tridimensional, se puede incrustar suavemente como un subconjunto cerrado del espacio euclidiano de cuatro dimensiones. ^[47]

La forma de energía mínima de una tira lisa de Möbius pegada a partir de un rectángulo no tiene una descripción analítica conocida, pero puede calcularse numéricamente y ha sido objeto de mucho estudio en teoría de placas desde el trabajo inicial sobre este tema en 1930 por Michael . Sadowski . ^{[39] [40]} También es posible encontrar superficies algebraicas que contengan tiras de Möbius desarrollables rectangulares. ^{[48] ​​[49]}

Hacer que el límite sea circular

El borde, o límite , de una franja de Möbius es topológicamente equivalente a un círculo . En las formas comunes de la tira de Möbius, tiene una forma diferente a la de un círculo, pero no está anudada y, por lo tanto, toda la tira se puede estirar sin cruzarse para hacer que el borde sea perfectamente circular. ^[50] Un ejemplo de ello se basa en la topología de la botella de Klein , una superficie unilateral sin límites que no puede incrustarse en un espacio tridimensional, pero puede sumergirse (permitiendo que la superficie se cruce a sí misma de ciertas maneras restringidas). . Una botella de Klein es la superficie que resulta cuando dos tiras de Möbius se pegan de borde a borde y, invirtiendo ese proceso, se puede cortar una botella de Klein a lo largo de un corte cuidadosamente elegido para producir dos tiras de Möbius. ^[51] Para una forma de botella de Klein conocida como botella de Klein de Lawson, la curva a lo largo de la cual se corta se puede hacer circular, lo que da como resultado tiras de Möbius con bordes circulares. ^[52]

La botella Klein de Lawson es una superficie mínima que se cruza sola en la hiperesfera unitaria del espacio de 4 dimensiones, el conjunto de puntos de la forma

$${\displaystyle (\cos \theta \cos \phi ,\sin \theta \cos \phi ,\cos 2\theta \sin \phi ,\sin 2\theta \sin \phi )}$$

. ^[53]gran círculolímite. ^[54]década de 1970. ^[55]círculos barridos. ^{[52] [56]} La proyección estereográficalímite. ^[52]línea central. ^[54]grupo ortogonal ,círculo. ^[53] ${\displaystyle 0\leq \theta <\pi ,0\leq \phi <2\pi }$ ${\displaystyle 0\leq \phi <\pi }$ ${\displaystyle \mathrm {O} (2)}$

Representación esquemática de una tapa en cruz con el fondo abierto, que muestra sus conjuntos de niveles . Esta superficie se cruza a sí misma a lo largo del segmento de línea vertical.

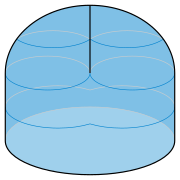
La franja de Möbius sudanesa se extiende por todos los lados de su círculo delimitador, algo inevitable si se quiere que la superficie no se cruce sobre sí misma. Otra forma de la tira de Möbius, llamada cross-cap o crosscap , también tiene un límite circular, pero por lo demás permanece en solo un lado del plano de este círculo, ^[57] lo que la hace más conveniente para unirla a agujeros circulares en otras superficies. . Para ello se santigua. Se puede formar quitando un cuadrilátero de la parte superior de un hemisferio, orientando los bordes del cuadrilátero en direcciones alternas y luego pegando pares opuestos de estos bordes de manera consistente con esta orientación. ^[58] Las dos partes de la superficie formada por los dos pares de bordes pegados se cruzan entre sí con un punto de pellizco como el de un paraguas Whitney en cada extremo del segmento de cruce, ^[59] la misma estructura topológica vista en el conoide de Plücker . ^[26]

Superficies de curvatura constante.

La franja de Möbius abierta es el interior relativo de una franja de Möbius estándar, formada omitiendo los puntos en su borde límite. Se le puede dar una geometría riemanniana de curvatura gaussiana constante positiva, negativa o cero . Los casos de curvatura negativa y cero forman superficies geodésicas completas, lo que significa que todas las geodésicas ("líneas rectas" en la superficie) pueden extenderse indefinidamente en cualquier dirección.

Curvatura cero

Se puede construir una tira abierta con curvatura cero pegando los lados opuestos de una tira plana entre dos líneas paralelas, descritas anteriormente como haz de líneas tautológicas. ^[46] La métrica resultante convierte la franja de Möbius abierta en una superficie plana (geodésicamente) completa (es decir, que tiene curvatura gaussiana cero en todas partes). Esta es la métrica única en la banda de Möbius, hasta una escala uniforme, que es a la vez plana y completa. Es el espacio cociente de un plano por reflexión de deslizamiento y (junto con el plano, el cilindro , el toroide y la botella de Klein ) es una de las cinco variedades planas completas bidimensionales . ^[60]

Curvatura negativa

La tira de Möbius abierta también admite métricas completas de curvatura negativa constante. Una forma de ver esto es comenzar con el modelo del semiplano superior (Poincaré) del plano hiperbólico , una geometría de curvatura constante cuyas líneas están representadas en el modelo por semicírculos que se encuentran con el eje en ángulos rectos. Tome el subconjunto del semiplano superior entre dos semicírculos anidados e identifique el semicírculo exterior con la inversión de izquierda a derecha del semicírculo interior. El resultado es topológicamente una tira de Möbius completa y no compacta con curvatura negativa constante. Es una superficie hiperbólica completa "no estándar" en el sentido de que contiene un semiplano hiperbólico completo (en realidad dos, en lados opuestos del eje de planeo-reflexión), y es una de las 13 superficies no estándar. ^[61] Nuevamente, esto puede entenderse como el cociente del plano hiperbólico por una reflexión de planeo. ^[62] ${\displaystyle x}$

Curvatura positiva

Una cinta de Möbius de curvatura positiva constante no puede ser completa, ya que se sabe que las únicas superficies completas de curvatura positiva constante son la esfera y el plano proyectivo . ^[60] Sin embargo, en cierto sentido está a sólo un punto de ser una superficie completa, ya que la tira de Möbius abierta es homeomorfa al plano proyectivo una vez perforado , la superficie que se obtiene eliminando cualquier punto del plano proyectivo. ^[63]

Se describe que las superficies mínimas tienen una curvatura media cero constante en lugar de una curvatura gaussiana constante. La franja de Möbius sudanesa se construyó como una superficie mínima limitada por un gran círculo en una esfera de 3, pero también hay una superficie mínima completa (sin límites) única inmersa en el espacio euclidiano que tiene la topología de una franja de Möbius abierta. Se llama tira de Meeks Möbius, ^[64] por su descripción de 1982 realizada por William Hamilton Meeks, III . ^[65] Aunque globalmente inestable como superficie mínima, pequeños parches de ella, delimitados por curvas no contráctiles dentro de la superficie, pueden formar tiras de Möbius incrustadas estables como superficies mínimas. ^[66] Tanto la franja de Meeks Möbius como cada superficie mínima de dimensiones superiores con la topología de la franja de Möbius se pueden construir utilizando soluciones al problema de Björling , que define una superficie mínima únicamente a partir de su curva límite y planos tangentes a lo largo de esta curva . . ^[67]

espacios de lineas

A la familia de líneas en el plano se le puede dar la estructura de un espacio suave, con cada línea representada como un punto en este espacio. El espacio de líneas resultante es topológicamente equivalente a la franja de Möbius abierta. ^[68] Una forma de ver esto es extender el plano euclidiano al plano proyectivo real agregando una línea más, la línea en el infinito . Por dualidad proyectiva el espacio de líneas en el plano proyectivo es equivalente a su espacio de puntos, el propio plano proyectivo. Quitar la línea en el infinito, para producir el espacio de líneas euclidianas, perfora este espacio de líneas proyectivas. ^[69] Por lo tanto, el espacio de las líneas euclidianas es un plano proyectivo perforado, que es una de las formas de la franja de Möbius abierta. ^[63] El espacio de líneas en el plano hiperbólico puede parametrizarse mediante pares desordenados de puntos distintos en un círculo, los pares de puntos en el infinito de cada línea. Este espacio, nuevamente, tiene la topología de una franja de Möbius abierta. ^[70]

Estos espacios de líneas son muy simétricos. Las simetrías de las líneas euclidianas incluyen las transformaciones afines , y las simetrías de las líneas hiperbólicas incluyen las transformaciones de Möbius . ^[71] Las transformaciones afines y las transformaciones de Möbius forman grupos de Lie de 6 dimensiones , espacios topológicos que tienen una estructura algebraica compatible que describe la composición de simetrías. ^{[72] [73]} Debido a que cada línea en el plano es simétrica a cualquier otra línea, la franja de Möbius abierta es un espacio homogéneo , un espacio con simetrías que llevan cada punto a cada otro punto. Los espacios homogéneos de grupos de Lie se denominan variedades de solv , y la banda de Möbius se puede utilizar como contraejemplo , mostrando que no toda variedad de solv es una variedad nula , y que no toda variedad de solv puede factorizarse en un producto directo de una variedad de solv compacta con . Estas simetrías también proporcionan otra forma de construir la propia tira de Möbius, como modelo grupal de estos grupos de Lie. Un modelo de grupo consta de un grupo de Lie y un subgrupo estabilizador de su acción; contraer las clases laterales del subgrupo a puntos produce un espacio con la misma topología que el espacio homogéneo subyacente. En el caso de las simetrías de líneas euclidianas, el estabilizador del eje está formado por todas las simetrías que toman el eje consigo mismo. Cada línea corresponde a una clase lateral, el conjunto de simetrías que se asignan al eje. Por tanto, el espacio cociente , un espacio que tiene un punto por clase lateral y hereda su topología del espacio de simetrías, es lo mismo que el espacio de rectas, y es nuevamente una franja de Möbius abierta. ^[74] ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x}$ ${\displaystyle \ell }$ ${\displaystyle \ell }$ ${\displaystyle x}$

Aplicaciones

Flujo eléctrico en una resistencia de Möbius.

Más allá de las aplicaciones ya comentadas de las tiras de Möbius al diseño de correas mecánicas que se desgastan uniformemente en toda su superficie, y del conoide de Plücker al diseño de engranajes, otras aplicaciones de las tiras de Möbius incluyen:

• Cintas de grafeno retorcidas para formar tiras de Möbius con nuevas características electrónicas, incluido el magnetismo helicoidal ^[75]
• Aromaticidad de Möbius , una propiedad de las sustancias químicas orgánicas cuya estructura molecular forma un ciclo, con orbitales moleculares alineados a lo largo del ciclo en el patrón de una tira de Möbius ^{[76] [77]}
• La resistencia de Möbius , una tira de material conductor que cubre el único lado de una tira dieléctrica de Möbius, de una manera que cancela su propia autoinductancia ^{[78] [79]}
• Resonadores con un diseño compacto y una frecuencia de resonancia que es la mitad que la de bobinas lineales construidas de manera idéntica ^{[80] [81]}
• Patrones de polarización en la luz que emerge de una placa q ^[82]
• Una prueba de la imposibilidad de reglas de agregación bipartidistas continuas, anónimas y unánimes en la teoría de la elección social ^[83]
• Montañas rusas circulares de Möbius , una forma de montaña rusa de doble vía en la que las dos vías giran entre sí un número impar de veces, de modo que los vagones regresan a la otra vía distinta a la que comenzaron ^{[84] [85]}
• Mapas del mundo proyectados sobre una franja de Möbius con las convenientes propiedades de que no hay límites este-oeste y que la antípoda de cualquier punto del mapa se puede encontrar en el otro lado impreso de la superficie en el mismo punto de la franja de Möbius ^{. 86] [87]}

Los científicos también han estudiado la energía de las películas de jabón con forma de tiras de Möbius, ^{[88] [89]} la síntesis química de moléculas con forma de tira de Möbius, ^{[90] [91] y la formación de tiras de Möbius a} nanoescala más grandes utilizando origami de ADN . ^[92]

En la cultura popular

Giro sin fin , Max Bill , 1956, del Museo de Escultura al Aire Libre de Middelheim

Las obras de arte bidimensionales que presentan la tira de Möbius incluyen una pintura sin título de 1947 de Corrado Cagli (conmemorada en un poema de Charles Olson ), ^{[93] [94]} y dos grabados de MC Escher : Möbius Band I (1961), que representa tres peces planos plegados. morderse la cola unos a otros; y Möbius Band II (1963), que representa hormigas arrastrándose alrededor de una tira de Möbius en forma de lemniscata . ^{[95] [96]} También es un tema popular de la escultura matemática , incluidas obras de Max Bill ( Endless Ribbon , 1953), José de Rivera ( Infinity , 1967) y Sebastián . ^[93] En Immortality (1982) de John Robinson se utilizó una tira de Möbius anudada en forma de trébol . ^[97] Continuum (1976) de Charles O. Perry es una de varias piezas de Perry que exploran variaciones de la tira de Möbius. ^[98]

Por su forma fácilmente reconocible, las tiras de Möbius son un elemento común del diseño gráfico . ^[97] El conocido logotipo de tres flechas para el reciclaje , diseñado en 1970, se basa en la forma triangular suave de la tira de Möbius, ^[99] al igual que el logotipo de la Expo '74 de temática medioambiental . ^[100] Algunas variaciones del símbolo de reciclaje utilizan una incrustación diferente con tres medias vueltas en lugar de una, ^[99] y la versión original del logotipo de Google Drive utilizaba una tira de Möbius de tres vueltas doblada plana, al igual que otros diseños similares. . ^[101] El Instituto Nacional de Matemática Pura e Aplicada (IMPA) de Brasil utiliza una tira de Möbius suave y estilizada como logotipo y tiene una gran escultura a juego de una tira de Möbius en exhibición en su edificio. ^[102] La tira de Möbius también ha aparecido en la obra de arte de sellos postales de países como Brasil, Bélgica, Países Bajos y Suiza. ^{[103] [104]}

Entrada al Salón de la Fama de NASCAR

Las tiras de Möbius han sido una inspiración frecuente para el diseño arquitectónico de edificios y puentes. Sin embargo, muchos de estos son proyectos o diseños conceptuales más que objetos construidos, o extienden su interpretación de la cinta de Möbius más allá de su reconocibilidad como una forma matemática o una parte funcional de la arquitectura. ^{[105] [106]} Un ejemplo es la Biblioteca Nacional de Kazajstán , para la cual se planeó un edificio con la forma de una tira de Möbius engrosada, pero se renovó con un diseño diferente después de que los arquitectos originales se retiraron del proyecto. ^[107] Un edificio notable que incorpora una franja de Möbius es el Salón de la Fama de NASCAR , que está rodeado por una gran cinta retorcida de acero inoxidable que actúa como fachada y dosel, y evoca las formas curvas de las pistas de carreras. ^[108] A menor escala, Moebius Chair (2006) de Pedro Reyes es un banco de cortejo cuya base y costados tienen forma de tira de Möbius. ^[109] Como una forma de matemáticas y artes de la fibra , las bufandas se han tejido en tiras de Möbius desde el trabajo de Elizabeth Zimmermann a principios de la década de 1980. ^[110] En el diseño de alimentos , las tiras de Möbius se han utilizado para cortar bagels , ^[111] hacer bucles con tocino , ^[112] y crear nuevas formas para pasta . ^[113]

Aunque matemáticamente la cinta de Möbius y la cuarta dimensión son conceptos puramente espaciales, a menudo han sido invocados en la ficción especulativa como base para un bucle temporal en el que las víctimas desprevenidas pueden quedar atrapadas. Ejemplos de este tropo incluyen "El profesor sin lados" (1946) de Martin Gardner, " Un metro llamado Mobius " (1950) de Armin Joseph Deutsch y la película Moebius (1996) basada en ella. Un mundo entero con forma de tira de Möbius es el escenario de "El muro de las tinieblas" (1946) de Arthur C. Clarke , mientras que las tiras de Möbius convencionales se utilizan como ingeniosos inventos en múltiples historias de William Hazlett Upson de los años 1940. ^[114] Se ha analizado que otras obras de ficción tienen una estructura similar a una tira de Möbius, en la que elementos de la trama se repiten con un giro; entre ellos se incluyen En busca del tiempo perdido (1913-1927) de Marcel Proust , Seis personajes en busca de un autor (1921) de Luigi Pirandello , Es una vida maravillosa (1946) de Frank Capra , Perdidos en the Funhouse ( 1968), Dhalgren de Samuel R. Delany (1975) y la película Donnie Darko (2001). ^[115]

Uno de los cánones musicales de JS Bach , el quinto de 14 cánones ( BWV 1087 ) descubierto en 1974 en la copia de Bach de las Variaciones Goldberg , presenta una simetría deslizamiento-reflexión en la que cada voz en el canon repite, con notas invertidas , lo mismo. motivo de dos compases anteriores. Debido a esta simetría, se puede pensar que este canon tiene su partitura escrita en una tira de Möbius. ^{[116] [h]} En teoría musical , los tonos que difieren en una octava generalmente se consideran notas equivalentes, y el espacio de notas posibles forma un círculo, el círculo cromático . Debido a que la cinta de Möbius es el espacio de configuración de dos puntos desordenados en un círculo, el espacio de todos los acordes de dos notas toma la forma de una cinta de Möbius. Esta concepción, y generalizaciones a más puntos, es una aplicación significativa de orbifolds a la teoría musical . ^{[117] [118]} Los grupos musicales modernos que toman su nombre de la tira de Möbius incluyen el trío estadounidense de rock electrónico Mobius Band ^[119] y la banda noruega de rock progresivo Ring Van Möbius . ^[120]

Las tiras de Möbius y sus propiedades se han utilizado en el diseño de magia escénica . Uno de esos trucos, conocido como bandas afganas, utiliza el hecho de que la tira de Möbius sigue siendo una sola tira cuando se corta a lo largo. Se originó en la década de 1880 y fue muy popular en la primera mitad del siglo XX. Existen muchas versiones de este truco y han sido realizadas por ilusionistas famosos como Harry Blackstone Sr. y Thomas Nelson Downs . ^{[121] [122]}

Ver también

• Contador de Möbius , un registro de desplazamiento cuyo bit de salida se complementa antes de retroalimentarse al bit de entrada
• Triángulo de Penrose , una figura imposible cuyo límite parece envolverlo en una cinta de Möbius
• Teoría de la cinta , la teoría matemática de tiras infinitamente delgadas que siguen curvas espaciales anudadas
• Atractor de Smale-Williams , un fractal formado al engrosar repetidamente una curva espacial hasta formar una franja de Möbius y luego reemplazarla con el borde límite.
• toro umbilical

Notas

1. Se pronuncia EE. UU .: / ˈ m oʊ b i ə s , ˈ m eɪ -/ MOH -bee-əs, MAYO - , Reino Unido : / ˈ m ɜː b i ə s / ; ^[1] Alemán: [ˈmøːbi̯ʊs] . Como es común en las palabras que contienen diéresis , también suele escribirse Mobius o Moebius .
2. Esencialmente, Blackett (1982) da este ejemplo, pero para una botella de Klein en lugar de una tira de Möbius. ^[8]
3. La longitud de una tira se puede medir en su línea central o cortando la tira de Möbius resultante perpendicularmente a su límite para que forme un rectángulo.
4. La tira de Möbius plegada plana formada a partir de tres triángulos equiláteros no proviene de un complejo simplicial abstracto , porque los tres triángulos comparten los mismos tres vértices, mientras que los complejos simpliciales abstractos requieren que cada triángulo tenga un conjunto diferente de vértices.
5. Esta incrustación cilíndrica y plana por partes tiene una clase de suavidad y puede aproximarse con precisión arbitraria mediante incrustaciones (clase ) infinitamente diferenciables . ^[39] ${\displaystyle C^{2}}$ ${\displaystyle C^{\infty }}$
6. 12/7 es el número racional más simple en el rango de relaciones de aspecto, entre 1,695 y 1,73, para el cual se desconoce la existencia de una incrustación suave.
7. Estas superficies tienen clase de suavidad . Para un análisis más detallado de los supuestos de suavidad que obligan a que una incorporación sea desarrollable versus los supuestos bajo los cuales el teorema de Nash-Kuiper permite incorporaciones arbitrariamente flexibles, consulte los comentarios de Bartels y Hornung (2015), p. 116, siguiendo el teorema 2.2. ^[39] ${\displaystyle C^{1}}$
8. Las tiras de Möbius también se han utilizado para analizar muchos otros cánones de Bach y otros, pero en la mayoría de estos casos se podrían haber utilizado igualmente bien otras superficies circulares, como un cilindro. ^[116]

Referencias

1. Wells, John C. (2008). Diccionario de pronunciación Longman (3ª ed.). Longman. ISBN 978-1-4058-8118-0.
2. Recogida, Clifford A. (2005). La franja de Möbius: la maravillosa banda del Dr. August Möbius en matemáticas, juegos, literatura, arte, tecnología y cosmología. Prensa de boca de trueno. págs. 28 y 29. ISBN 978-1-56025-826-1.
3. Larison, Lorraine L. (1973). "La banda de Möbius en los mosaicos romanos". Científico americano . 61 (5): 544–547. Código bibliográfico : 1973AmSci..61..544L. JSTOR  27843983.
4. Cartwright, Julyan HE ; González, Diego L. (2016). "Möbius se desnuda antes que Möbius: pistas topológicas en representaciones antiguas". El inteligente matemático . 38 (2): 69–76. arXiv : 1609.07779 . Código Bib : 2016arXiv160907779C. doi :10.1007/s00283-016-9631-8. SEÑOR  3507121. S2CID  119587191.
5. Flapan, Erica (2000). Cuando la topología se encuentra con la química: una mirada topológica a la quiralidad molecular . Perspectivas. Washington, DC: Asociación Matemática de América. págs. 82–83. doi :10.1017/CBO9780511626272. ISBN 0-521-66254-0. SEÑOR  1781912.
6. Pickover (2005), págs. 8–9.
7. Woll, John W. Jr. (primavera de 1971). "Superficies unilaterales y orientabilidad". Revista universitaria de matemáticas de dos años . 2 (1): 5–18. doi :10.2307/3026946. JSTOR  3026946.
8. Blackett, Donald W. (1982). Topología elemental: un enfoque combinatorio y algebraico . Prensa académica. pag. 195.ISBN _ 9781483262536.
9. Frolkina, Olga D. (2018). "Bandas de Moebius separadas por pares en el espacio". Revista de teoría de nudos y sus ramificaciones . 27 (9): 1842005, 9. arXiv : 2212.02983 . doi :10.1142/S0218216518420051. SEÑOR  3848635. S2CID  126421578.
10. Cordero, Evelyn (20 de febrero de 2019). "Las tiras de Möbius desafían un vínculo con el infinito". Revista Quanta .
11. Melikhov, Sergey A. (2019). "Una nota sobre el artículo de O. Frolkina "Bandas de Moebius separadas por pares en el espacio"". Revista de teoría de nudos y sus ramificaciones . 28 (7): 1971001, 3. arXiv : 1810.04089 . doi : 10.1142/s0218216519710019. SEÑOR  3975576. S2CID  119179202.
12. Recogida (2005), pág. 52.
13. Recogida (2005), pág. 12.
14. Kyle, RH (1955). "Incrustaciones de bandas de Möbius en un espacio tridimensional". Actas de la Real Academia Irlandesa, Sección A. 57 : 131-136. JSTOR  20488581. SEÑOR  0091480.
15. Recogida (2005), pág. 11.
16. Massey, William S. (1991). Un curso básico en topología algebraica. Textos de Posgrado en Matemáticas. vol. 127. Nueva York: Springer-Verlag. pag. 49.ISBN _ 0-387-97430-X. SEÑOR  1095046.
17. Rouse Ball, Guerra Mundial (1892). "Anillos paradrómicos". Recreaciones y problemas matemáticos del pasado y del presente (2ª ed.). Londres y Nueva York: Macmillan y compañía. págs. 53–54. ISBN 9780608377803.
18. Bennett, GT (junio de 1923). "Anillos paradrómicos". Naturaleza . 111 (2800): 882. Bibcode :1923Natur.111R.882B. doi : 10.1038/111882b0 . S2CID  4099647.
19. Tietze, Heinrich (1910). "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" (PDF) . Jahresbericht der Deutschen Mathematiker-Vereinigung . 19 : 155-159.
20. Ringel, G .; Jóvenes, JWT (1968). "Solución del problema de coloración de mapas de Heawood". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 60 (2): 438–445. Código bibliográfico : 1968PNAS...60..438R. doi : 10.1073/pnas.60.2.438 . SEÑOR  0228378. PMC 225066 . PMID  16591648. 
21. Jablan, Slavik; Radovic, Ljiljana; Sazdanović, Radmila (2011). "Gráficos no planos derivados de códigos Gauss de nudos y enlaces virtuales". Revista de Química Matemática . 49 (10): 2250–2267. doi :10.1007/s10910-011-9884-6. SEÑOR  2846715. S2CID  121332704.
22. Larsen, Mogens Esrom (1994). "Entender mal mis laberintos puede hacerme sentir miserable". En Guy, Richard K .; Woodrow, Robert E. (eds.). Actas de la Conferencia en memoria de Eugène Strens sobre matemáticas recreativas y su historia celebrada en la Universidad de Calgary, Calgary, Alberta, agosto de 1986 . Espectro MAA. Washington, DC: Asociación Matemática de América. págs. 289–293. ISBN 0-88385-516-X. SEÑOR  1303141.. Consulte la Figura 7, pág. 292.
23. Maschke, Heinrich (1900). "Nota sobre la superficie unilateral de Moebius". Transacciones de la Sociedad Matemática Estadounidense . 1 (1): 39. doi : 10.2307/1986401 . JSTOR  1986401. SEÑOR  1500522.
24. Junghenn, Hugo D. (2015). Un curso de análisis real. Boca Ratón, Florida: CRC Press. pag. 430.ISBN _ 978-1-4822-1927-2. SEÑOR  3309241.
25. Séquin, Carlo H. (2005). "División de toros, nudos y bandas de Moebius". En Sarhangi, Reza; Moody, Robert V. (eds.). Renaissance Banff: matemáticas, música, arte, cultura . Southwestern College, Winfield, Kansas: Conferencia Bridges. págs. 211-218. ISBN 0-9665201-6-5.
26. Francis, George K. (1987). "Conoide de Plücker". Un libro ilustrado topológico . Springer-Verlag, Nueva York. págs. 81–83. ISBN 0-387-96426-6. SEÑOR  0880519.
27. Dooner, David B.; Seireg, Ali (1995). "3.4.2 El cilindroide". La geometría cinemática del engranaje: un enfoque de ingeniería concurrente . Serie Wiley en Ingeniería de Diseño. vol. 3. John Wiley e hijos. págs. 135-137. ISBN 9780471045977.
28. Barr, Stephen (1964). Experimentos en topología. Nueva York: Thomas Y. Crowell Company. págs. 40–49, 200–201. ISBN 9780690278620.
29. Fuchs, Dmitry ; Tabachnikov, Serge (2007). "Conferencia 14: Banda de Paper Möbius". Ómnibus matemático: treinta conferencias sobre matemáticas clásicas (PDF) . Providence, Rhode Island: Sociedad Matemática Estadounidense. págs. 199-206. doi :10.1090/mbk/046. ISBN 978-0-8218-4316-1. SEÑOR  2350979. Archivado desde el original (PDF) el 24 de abril de 2016.
30. Pook, Les (2003). "4.2: Revisión del trihexaflexágono". Flexágonos de adentro hacia afuera . Cambridge, Reino Unido: Cambridge University Press. págs. 33–36. doi :10.1017/CBO9780511543302. ISBN 0-521-81970-9. SEÑOR  2008500.
31. Kühnel, W.; Banchoff, TF (1983). "El plano proyectivo complejo de 9 vértices" (PDF) . El inteligente matemático . 5 (3): 11-22. doi :10.1007/BF03026567. SEÑOR  0737686. S2CID  120926324.
32. Kuiper, Nicolaas H. (1972). "Incrustaciones topológicas estrechas de la banda de Moebius". Revista de Geometría Diferencial . 6 (3): 271–283. doi : 10.4310/jdg/1214430493 . SEÑOR  0314057.
33. Szilassi, Lajos (2008). "Un modelo poliédrico en el espacio tridimensional euclidiano del mapa de seis pentágonos del plano proyectivo". Geometría discreta y computacional . 40 (3): 395–400. doi : 10.1007/s00454-007-9033-y . SEÑOR  2443291. S2CID  38606607.
34. Tuckerman, Bryant (1948). "Una banda de Möbius poliédrica no singular cuyo límite es un triángulo". Mensual Matemático Estadounidense . 55 (5): 309–311. doi :10.2307/2305482. JSTOR  2305482. SEÑOR  0024138.
35. Bonnington, C. Paul; Nakamoto, Atsuhiro (2008). "Realización geométrica de una triangulación sobre el plano proyectivo con una cara eliminada". Geometría discreta y computacional . 40 (1): 141-157. doi : 10.1007/s00454-007-9035-9 . SEÑOR  2429652. S2CID  10887519.
36. Brehm, Ulrich (1983). "Una tira de Möbius triangulada no poliédrica". Actas de la Sociedad Matemática Estadounidense . 89 (3): 519–522. doi :10.2307/2045508. JSTOR  2045508. SEÑOR  0715878.
37. Nakamoto, Atsuhiro; Tsuchiya, Shoichi (2012). "Sobre triangulaciones de Möbius geométricamente realizables". Matemáticas discretas . 312 (14): 2135–2139. doi : 10.1016/j.disc.2011.06.007 . SEÑOR  2921579.
38. Hinz, Denis F.; Frito, Eliot (2015). "Traducción del artículo de Michael Sadowsky "Una prueba elemental de la existencia de una banda de Möbius desarrollable y la atribución del problema geométrico a un problema variacional"". Revista de elasticidad . 119 (1–2): 3–6. arXiv : 1408.3034 . doi :10.1007/s10659-014-9490-5. SEÑOR  3326180. S2CID  119733903.Reimpreso en Fosdick, Roger; Frito, Eliot (2016). La mecánica de cintas y bandas de Möbius (PDF) . Springer, Dordrecht. págs. 3–6. doi :10.1007/978-94-017-7300-3. ISBN 978-94-017-7299-0. SEÑOR  3381564.
39. Bartels, Sören; Hornung, Peter (2015). "Doblado de papel y tira de Möbius". Revista de Elasticidad . 119 (1–2): 113–136. doi :10.1007/s10659-014-9501-6. SEÑOR  3326187. S2CID  119782792.Reimpreso en Fosdick & Fried (2016), págs. 113-136. Véase en particular la Sección 5.2, págs. 129 y 130.
40. Starostin, EL; van der Heijden, GHM (2015). "Formas de equilibrio con localización de tensiones para tiras elásticas inextensibles de Möbius y otras". Revista de Elasticidad . 119 (1–2): 67–112. doi : 10.1007/s10659-014-9495-0 . SEÑOR  3326186. S2CID  53462568.Reimpreso en Fosdick & Fried (2016), págs. 67-112.
41. Schwarz, Gideon E. (1990). "El lado oscuro de la franja de Moebius". El Mensual Matemático Estadounidense . 97 (10): 890–897. doi :10.1080/00029890.1990.11995680. JSTOR  2324325. SEÑOR  1079975.
42. Halpern, B.; Tejedor, C. (1977). "Inversión de un cilindro mediante inmersiones isométricas e incrustaciones isométricas". Transacciones de la Sociedad Matemática Estadounidense . 230 : 41–70. doi : 10.2307/1997711 . JSTOR  1997711. SEÑOR  0474388.
43. Schwartz, Richard Evan (2021). "Una encuadernación mejorada en la banda de Moebius de papel óptima". Geometriae Dedicata . 215 : 255–267. arXiv : 2008.11610 . doi :10.1007/s10711-021-00648-5. SEÑOR  4330341. S2CID  220279013.
44. Schwartz, Richard (2023). "La banda de Moebius de papel óptima". arXiv : 2308.12641 [matemáticas.MG].
45. Crowell, Rachel (12 de septiembre de 2023). "Los matemáticos resuelven un rompecabezas de tiras de Möbius de 50 años". Científico americano .
46. Dundas, Bjørn Ian (2018). "Ejemplo 5.1.3: La banda ilimitada de Möbius". Un curso breve en topología diferencial . Libros de texto de matemáticas de Cambridge. Prensa de la Universidad de Cambridge, Cambridge. pag. https://books.google.com/books?id=7a1eDwAAQBAJ&pg=PA101. doi :10.1017/9781108349130. ISBN 978-1-108-42579-7. SEÑOR  3793640. S2CID  125997451.
47. Blanuša, Danilo (1954). "La extensión isométrica de la banda de Möbius infinitamente grande euclidiana en un espacio esférico, parabólico o hiperbólico en cuatro dimensiones". Boletín Internacional de la Academia Yougoslave des Sciences et des Beaux-Arts . 12 : 19-23. SEÑOR  0071060.
48. Wunderlich, W. (1962). "Über ein abwickelbares Möbiusband". Monatshefte für Mathematik . 66 (3): 276–289. doi :10.1007/BF01299052. SEÑOR  0143115. S2CID  122215321.
49. Schwarz, Gedeón (1990). "Un pretendiente al título 'tira canónica de Moebius'". Revista Pacífico de Matemáticas . 143 (1): 195-200. doi : 10.2140/pjm.1990.143.195 . SEÑOR  1047406.
50. Hilbert, David ; Cohn-Vossen, Stephan (1952). Geometría e imaginación (2ª ed.). Chelsea. págs. 315–316. ISBN 978-0-8284-1087-8.
51. Spivak, Michael (1979). Una introducción completa a la geometría diferencial, volumen I (2ª ed.). Wilmington, Delaware: publicar o morir. pag. 591.
52. Knöppel, Felix (verano de 2019). "Tutorial 3: Superficies mínimas de Lawson y la banda de Möbius sudanesa". DDG2019: Curso de visualización en TU Berlin .
53. Lawson, H. Blaine Jr. (1970). "Superficies mínimas completas en ". Anales de Matemáticas . Segunda Serie. 92 (3): 335–374. doi :10.2307/1970625. JSTOR  1970625. SEÑOR  0270280. ${\displaystyle S^{3}}$Consulte la Sección 7, págs. 350-353, donde se denota la botella de Klein . ${\displaystyle \tau _{1,2}}$
54. Schleimer, Saúl; Segerman, Henry (2012). "Esculturas en S3". En El Bosco, Robert; McKenna, Douglas; Sarhangi, Reza (eds.). Actas de Bridges 2012: Matemáticas, Música, Arte, Arquitectura, Cultura . Phoenix, Arizona: Publicación de Teselaciones. págs. 103-110. arXiv : 1204.4952 . ISBN 978-1-938664-00-7.
55. Gunn, Charles (23 de agosto de 2018). "Banda Sudanesa de Möbius". Vimeo . Consultado el 17 de marzo de 2022 .
56. Franzoni, Gregorio (2012). "La botella de Klein: variaciones sobre un tema". Avisos de la Sociedad Matemática Estadounidense . 59 (8): 1076–1082. doi : 10.1090/noti880 . SEÑOR  2985809.
57. Huggett, Stephen; Jordania, David (2009). Un aperitivo topológico (edición revisada). Springer-Verlag. pag. 57.ISBN _ 978-1-84800-912-7. SEÑOR  2483686.
58. Flapán, Erica (2016). Nudos, moléculas y el universo: una introducción a la topología. Providence, Rhode Island: Sociedad Matemática Estadounidense. págs. 99-100. doi :10.1090/mbk/096. ISBN 978-1-4704-2535-7. SEÑOR  3443369.
59. Richeson, David S. (2008). La gema de Euler: la fórmula del poliedro y el nacimiento de la topología . Princeton, Nueva Jersey: Princeton University Press. pag. 171.ISBN _ 978-0-691-12677-7. SEÑOR  2440945.
60. Godinho, Leonor; Natário, José (2014). Introducción a la geometría de Riemann: con aplicaciones a la mecánica y la relatividad. Texto universitario. Springer, Cham. págs. 152-153. doi :10.1007/978-3-319-08666-8. ISBN 978-3-319-08665-1. SEÑOR  3289090.
61. Cantwell, Juan; Conlon, Lawrence (2015). "Geometría hiperbólica y homeomorfismos homotópicos de superficies". Geometriae Dedicata . 177 : 27–42. arXiv : 1305.1379 . doi :10.1007/s10711-014-9975-1. SEÑOR  3370020. S2CID  119640200.
62. Stillwell, John (1992). "4.6 Clasificación de isometrías". Geometría de Superficies . Texto universitario. Cham: Springer. págs. 96–98. doi :10.1007/978-1-4612-0929-4. ISBN 0-387-97743-0. SEÑOR  1171453.
63. Seifert, Herbert ; Threlfall, William (1980). Un libro de texto de topología. Matemática Pura y Aplicada. vol. 89. Traducido por Goldman, Michael A. Nueva York y Londres: Academic Press. pag. 12.ISBN _ 0-12-634850-2. SEÑOR  0575168.
64. López, Francisco J.; Martín, Francisco (1997). "Superficies mínimas completas no orientables con el grupo de simetría más alto". Revista Estadounidense de Matemáticas . 119 (1): 55–81. doi :10.1353/ajm.1997.0004. SEÑOR  1428058. S2CID  121366986.
65. Meeks, William H. III (1981). "La clasificación de superficies mínimas completas en con curvatura total mayor que ". Revista de Matemáticas de Duke . 48 (3): 523–535. doi :10.1215/S0012-7094-81-04829-8. SEÑOR  0630583. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle -8\pi }$
66. Pesci, Adriana I .; Goldstein, Raymond E .; Alejandro, Gareth P.; Moffatt, H. Keith (2015). "Inestabilidad de una superficie mínima de una tira de Möbius y su vínculo con la geometría sistólica" (PDF) . Cartas de revisión física . 114 (12): 127801. Código bibliográfico : 2015PhRvL.114l7801P. doi : 10.1103/PhysRevLett.114.127801. SEÑOR  3447638. PMID  25860771.
67. Mira, Pablo (2006). "Completa las tiras mínimas de Möbius y el problema de Björling". Revista de Geometría y Física . 56 (9): 1506-1515. Código Bib : 2006JGP....56.1506M. doi :10.1016/j.geomphys.2005.08.001. SEÑOR  2240407. ${\displaystyle \mathbb {R} ^{n}}$
68. Parker, Phillip E. (1993). "Espacios de geodésicas". En Del Riego, L. (ed.). Taller de Geometría Diferencial en Espacios de Geometría (Guanajuato, 1992) . Aportaciones Mat. Notas Investigación. vol. 8. Soc. Estera. Mexicana, México. págs. 67–79. SEÑOR  1304924.
69. Bickel, Holger (1999). "Dualidad en planos estables y operaciones de cierre y kernel relacionadas". Revista de Geometría . 64 (1–2): 8–15. doi :10.1007/BF01229209. SEÑOR  1675956. S2CID  122209943.
70. Mangahas, Johanna (julio de 2017). "Hora de oficina cinco: el lema del ping-pong". En arcilla, Matt; Margalit, Dan (eds.). Horas de oficina con un teórico de grupos geométricos . Prensa de la Universidad de Princeton. págs. 85-105. doi :10.1515/9781400885398. ISBN 9781400885398.Véase en particular el Proyecto 7, págs. 104-105.
71. Ramírez Galarza, Ana Irene; Seade, José (2007). Introducción a las Geometrías Clásicas . Basilea: Birkhäuser Verlag. págs. 83–88, 157–163. ISBN 978-3-7643-7517-1. SEÑOR  2305055.
72. Fomenko, Anatolij T .; Kunii, Tosiyasu L. (2013). Modelado topológico para visualización. Saltador. pag. 269.ISBN _ 9784431669562.
73. Isham, Chris J. (1999). Geometría diferencial moderna para físicos. Apuntes de conferencias de World Scientific sobre física. vol. 61 (2ª ed.). Científico mundial. pag. 269.ISBN _ 981-02-3555-0. SEÑOR  1698234.
74. Gorbatsevich, VV; Onishchik, AL; Vinberg, È. B. (1993). Grupos de mentiras y álgebras de mentiras I: fundamentos de la teoría de la mentira; Grupos de transformación de mentiras. Enciclopedia de Ciencias Matemáticas. vol. 20. Springer-Verlag, Berlín. págs. 164-166. doi :10.1007/978-3-642-57999-8. ISBN 3-540-18697-2. SEÑOR  1306737.
75. Yamashiro, Atsushi; Shimoi, Yukihiro; Harigaya, Kikuo; Wakabayashi, Katsunori (2004). "Nuevos estados electrónicos en cintas de grafeno: órdenes de carga y giro competitivas". Física E. 22 (1–3): 688–691. arXiv : cond-mat/0309636 . Código Bib : 2004PhyE...22..688Y. doi :10.1016/j.physe.2003.12.100. S2CID  17102453.
76. Rzepa, Henry S. (septiembre de 2005). "Romaticidad y deslocalización de Möbius". Reseñas químicas . 105 (10): 3697–3715. doi :10.1021/cr030092l. PMID  16218564.
77. Yoon, Zin Seok; Osuka, Atsuhiro; Kim, Dongho (mayo de 2009). "Aromaticidad y antiaromaticidad de Möbius en porfirinas expandidas". Química de la Naturaleza . 1 (2): 113–122. Código Bib : 2009NatCh...1..113Y. doi :10.1038/nchem.172. PMID  21378823.
78. "Hacer resistencias con matemáticas". Tiempo . vol. 84, núm. 13. 25 de septiembre de 1964.
79. Recogida (2005), págs. 45–46.
80. Estanque, JM (2000). "Filtros de paso de banda y resonadores de modo dual Mobius". Transacciones IEEE sobre teoría y técnicas de microondas . 48 (12): 2465–2471. Código Bib : 2000ITMTT..48.2465P. doi : 10.1109/22.898999.
81. Rohde, Ulrich L.; Poddar, Ajay; Sundararajan, D. (noviembre de 2013). "Resonadores impresos: teoría y aplicaciones de la tira de Möbius" (PDF) . Diario de microondas . 56 (11).
82. Bauer, Thomas; Bánzer, Peter; Karimi, Ebrahim; Orlov, Sergej; Rubano, Andrea; Marrucci, Lorenzo; Santamato, Enrico; Boyd, Robert W.; Leuchs, Gerd (febrero de 2015). "Observación de tiras de Möbius de polarización óptica". Ciencia . 347 (6225): 964–966. Código Bib : 2015 Ciencia... 347.. 964B. doi : 10.1126/ciencia.1260635. PMID  25636796. S2CID  206562350.
83. Candeal, Juan Carlos; Induráin, Esteban (enero de 1994). "La tira de Moebius y una paradoja de la elección social". Cartas de Economía . 45 (3): 407–412. doi :10.1016/0165-1765(94)90045-0.
84. Easdown, Martín (2012). Parque de diversiones. Publicación de Bloomsbury. pag. 43.ISBN _ 9781782001522.
85. Gancho, Patrick (2019). Ticket To Ride: la guía esencial de las montañas rusas y atracciones emocionantes más grandes del mundo. Libros de Chartwell. pag. 20.ISBN _ 9780785835776.
86. Tobler, Waldo R. (1961). "Un mapa del mundo en una cinta de Möbius". Topografía y cartografía . 21 : 486.
87. Kumler, Mark P .; Tobler, Waldo R. (enero de 1991). "Tres mapas del mundo en una franja de Moebius". Cartografía y Sistemas de Información Geográfica . 18 (4): 275–276. doi :10.1559/152304091783786781.
88. Courant, Richard (1940). "Experimentos con películas de jabón con superficies mínimas". El Mensual Matemático Estadounidense . 47 (3): 167-174. doi :10.1080/00029890.1940.11990957. JSTOR  2304225. SEÑOR  0001622.
89. Goldstein, Raymond E .; Moffatt, H. Keith ; Pesci, Adriana I. ; Ricca, Renzo L. (diciembre de 2010). "La tira de Möbius de película de jabón cambia la topología con un giro singular". Procedimientos de la Academia Nacional de Ciencias . 107 (51): 21979–21984. Código Bib : 2010PNAS..10721979G. doi : 10.1073/pnas.1015997107 . PMC 3009808 . 
90. Walba, David M.; Richards, Rodney M.; Haltiwanger, R. Curtis (junio de 1982). "Síntesis total de la primera tira molecular de Moebius". Revista de la Sociedad Química Estadounidense . 104 (11): 3219–3221. doi :10.1021/ja00375a051.
91. Recogida (2005), págs. 52–58.
92. Gitig, Diana (18 de octubre de 2010). "Origami químico utilizado para crear una tira de ADN de Möbius". Ars Técnica . Consultado el 28 de marzo de 2022 .
93. Emmer, Michele (primavera de 1980). "Artes visuales y matemáticas: la banda de Moebius". Leonardo . 13 (2): 108–111. doi :10.2307/1577979. JSTOR  1577979. S2CID  123908555.
94. Byers, Mark (2018). Charles Olson y el modernismo estadounidense: la práctica del yo. Prensa de la Universidad de Oxford. págs. 77–78. ISBN 9780198813255.
95. Crato, Nuño (2010). "Escher y la tira de Möbius". Descubrirlo: encuentros entretenidos con las matemáticas cotidianas . Saltador. págs. 123-126. doi :10.1007/978-3-642-04833-3_29.
96. Kersten, Erik (13 de marzo de 2017). "Franja de Moebius I". Escher en el Palacio . Consultado el 17 de abril de 2022 .
97. Pickover (2005), pág. 13.
98. Brecher, Kenneth (2017). "Arte del infinito". En Swart, David; Séquin, Carlo H.; Fenyvesi, Kristóf (eds.). Actas de Bridges 2017: Matemáticas, Arte, Música, Arquitectura, Educación, Cultura . Phoenix, Arizona: Publicación de Teselaciones. págs. 153-158. ISBN 978-1-938664-22-9.
99. Peterson, Ivars (2002). "Topología de reciclaje". Viajes matemáticos: de números surrealistas a círculos mágicos . Espectro MAA. Asociación Matemática de América, Washington, DC. págs. 31–35. ISBN 0-88385-537-2. SEÑOR  1874198.
100. "Símbolo de la Expo '74 seleccionado". La revisión del portavoz . 12 de marzo de 1972. p. 1.
101. Millward, Steven (30 de abril de 2012). "¿Google Drive copió su icono de una aplicación china?". Tecnología en Asia . Consultado el 27 de marzo de 2022 - a través de Yahoo! Noticias.
102. "Símbolo del IMPA". Para quem é fã do IMPA, estas curiosidades sobre el instituto . IMPA. 7 de mayo de 2020 . Consultado el 27 de marzo de 2022 .
103. Recogida (2005), págs. 156-157.
104. Decker, Heinz; Rígido, Eberhard (1983). "Möbius-Bänder: ... und natürlich auch auf Briefmarken". Praxis der Mathematik . 25 (7): 207–215. SEÑOR  0720681.
105. Thulaseedas, alegre; Krawczyk, Robert J. (2003). "Conceptos de Möbius en arquitectura". En Barrallo, Javier; Friedman, Nathaniel; Maldonado, Juan Antonio; Mart\'\inez-Aroza, José; Sarhangi, Reza; Séquin, Carlo (eds.). Encuentro Alhambra, Actas del Congreso ISAMA-BRIDGES . Granada, España: Universidad de Granada. págs. 353–360. ISBN 84-930669-1-5.
106. Séquin, Carlo H. (enero de 2018). "Puentes de Moebius". Revista de Matemáticas y Artes . 12 (2–3): 181–194. doi :10.1080/17513472.2017.1419331. S2CID  216116708.
107. Wainwright, Oliver (17 de octubre de 2017). "'Norman dijo que el presidente quiere una pirámide: cómo los arquitectos estrella construyeron Astana ". El guardián .
108. Muret, Don (17 de mayo de 2010). "El Salón de la Fama de NASCAR 'parece rápido estando quieto'". Revista de Negocios Deportivos .
109. Gopnik, Blake (17 de octubre de 2014). "Pedro Reyes hace un sofá de dos plazas infinito". Noticias de Artnet .
110. Thomas, Nancy J. (4 de octubre de 1998). "Hacer de Mobius una cuestión de matemáticas". Los tiempos (Trenton) . pag. aa3 - vía NewsBank .
111. Pashman, Dan (6 de agosto de 2015). "Corta tu bagel de la forma matemáticamente correcta". La sal . NPR.
112. Miller, Ross (5 de septiembre de 2014). "Cómo hacer una tira de tocino matemáticamente infinita". El borde .
113. Chang, Kenneth (9 de enero de 2012). "La pasta se gradúa de la sopa de letras a la geometría avanzada". Los New York Times .
114. Recogida (2005), págs. 174-177.
115. Recogida (2005), págs. 179-187.
116. Phillips, Tony (25 de noviembre de 2016). "Bach y la tira musical de Möbius". Revista Más .Reimpreso de una columna destacada de la Sociedad Estadounidense de Matemáticas.
117. Moskowitz, Clara (6 de mayo de 2008). "Música reducida a hermosas matemáticas". Ciencia Viva . Consultado el 21 de marzo de 2022 .
118. Tymoczko, Dmitri (7 de julio de 2006). «La geometría de los acordes musicales» (PDF) . Ciencia . 313 (5783): 72–4. Código Bib : 2006 Ciencia... 313... 72T. doi : 10.1126/ciencia.1126287. JSTOR  3846592. PMID  16825563. S2CID  2877171.
119. Parks, Andrew (30 de agosto de 2007). "Mobius Band: Fuego amigo". Imán .
120. Lawson, Dom (9 de febrero de 2021). "Anillo Van Möbius". Prog .
121. Prevos, Peter (2018). La franja de Möbius en la magia: un tratado sobre las bandas afganas. Piso Canguro: Tercer Hemisferio.
122. Gardner, Martín (1956). "Las bandas afganas". Matemáticas, Magia y Misterio . Nueva York: Dover Books. págs. 70–73.

enlaces externos

• Weisstein, Eric W. "La franja de Möbius". MundoMatemático .