ecuación cúbica

Ecuación polinómica de grado 3.

Gráfica de una función cúbica con 3 raíces reales (donde la curva cruza el eje horizontal en y = 0 ). El caso mostrado tiene dos puntos críticos . Aquí la función es . ${\displaystyle f(x)={\frac {1}{4}}\left(x^{3}+3x^{2}-6x-8\right)}$

En álgebra , una ecuación cúbica en una variable es una ecuación de la forma

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

en el que a es distinto de cero.

Las soluciones de esta ecuación se llaman raíces de la función cúbica definida por el lado izquierdo de la ecuación. Si todos los coeficientes a , b , c y d de la ecuación cúbica son números reales , entonces tiene al menos una raíz real (esto es cierto para todas las funciones polinomiales de grado impar ). Todas las raíces de la ecuación cúbica se pueden encontrar de la siguiente manera:

• algebraicamente : más precisamente, se pueden expresar mediante una fórmula cúbica que involucra los cuatro coeficientes, las cuatro operaciones aritméticas básicas , las raíces cuadradas y las raíces cúbicas . (Esto también es cierto para las ecuaciones cuadráticas (de segundo grado) y cuárticas (de cuarto grado), pero no para las ecuaciones de grado superior, según el teorema de Abel-Ruffini .)
• trigonométricamente
• Se pueden encontrar aproximaciones numéricas de las raíces utilizando algoritmos de búsqueda de raíces como el método de Newton .

No es necesario que los coeficientes sean números reales. Gran parte de lo que se cubre a continuación es válido para coeficientes en cualquier campo con características distintas a 2 y 3. Las soluciones de la ecuación cúbica no necesariamente pertenecen al mismo campo que los coeficientes. Por ejemplo, algunas ecuaciones cúbicas con coeficientes racionales tienen raíces que son números complejos irracionales (e incluso no reales) .

Historia

Las ecuaciones cúbicas eran conocidas por los antiguos babilonios, griegos, chinos, indios y egipcios. ^{[1] [2] [3]} Se han encontrado tablillas cuneiformes babilónicas (siglos XX al XVI a. C.) con tablas para calcular cubos y raíces cúbicas. ^{[4] [5]} Los babilonios podrían haber usado las tablas para resolver ecuaciones cúbicas, pero no existe evidencia que confirme que lo hicieran. ^[6] El problema de duplicar el cubo involucra la ecuación cúbica más simple y antigua estudiada, y una para la cual los antiguos egipcios no creían que existiera una solución. ^[7] En el siglo V a. C., Hipócrates redujo este problema al de encontrar dos proporcionales medias entre una línea y otra de dos veces su longitud, pero no pudo resolverlo con una construcción con compás y regla , ^[8] una tarea que ahora es Se sabe que es imposible. Los métodos para resolver ecuaciones cúbicas aparecen en Los nueve capítulos sobre el arte matemático , un texto matemático chino compilado alrededor del siglo II a. C. y comentado por Liu Hui en el siglo III. ^[2]

En el siglo III d.C., el matemático griego Diofanto encontró soluciones enteras o racionales para algunas ecuaciones cúbicas bivariadas ( ecuaciones diofánticas ). ^{[3] [9]} Se cree que Hipócrates, Menecmo y Arquímedes estuvieron cerca de resolver el problema de duplicar el cubo usando secciones cónicas que se cruzan , ^[8] aunque historiadores como Reviel Netz cuestionan si los griegos estaban pensando en ecuaciones cúbicas o simplemente Problemas que pueden conducir a ecuaciones cúbicas. Algunos otros, como TL Heath , que tradujo todas las obras de Arquímedes, no están de acuerdo y presentan evidencia de que Arquímedes realmente resolvió ecuaciones cúbicas usando intersecciones de dos cónicas , pero también discutió las condiciones en las que las raíces son 0, 1 o 2. ^[10]

Gráfica de la función cúbica f ( x ) = 2 x ³  − 3 x ²  − 3 x  + 2 = ( x  + 1) (2 x  − 1) ( x  − 2)

En el siglo VII, el matemático astrónomo de la dinastía Tang Wang Xiaotong en su tratado matemático titulado Jigu Suanjing estableció sistemáticamente y resolvió numéricamente 25 ecuaciones cúbicas de la forma x ³ + px ² + qx = N , 23 de ellas con p , q ≠ 0 , y dos de ellos con q = 0 . ^[11]

En el siglo XI, el poeta y matemático persa Omar Khayyam (1048-1131) logró avances significativos en la teoría de las ecuaciones cúbicas. En uno de sus primeros artículos, descubrió que una ecuación cúbica puede tener más de una solución y afirmó que no se puede resolver utilizando construcciones con compás y regla. También encontró una solución geométrica. ^{[12] [a]} En su trabajo posterior, el ''Tratado sobre la demostración de problemas de álgebra'', escribió una clasificación completa de ecuaciones cúbicas con soluciones geométricas generales encontradas mediante secciones cónicas que se cruzan . ^{[13] [14]} Khayyam intentó idear una fórmula algebraica para extraer raíces cúbicas. El escribio:

“Hemos intentado expresar estas raíces mediante álgebra pero hemos fracasado. Sin embargo, puede ser que los hombres que vengan después de nosotros tengan éxito”. ^[15]

En el siglo XII, el matemático indio Bhaskara II intentó resolver ecuaciones cúbicas sin éxito general. Sin embargo, dio un ejemplo de ecuación cúbica: x ³ + 12 x = 6 x ² + 35 . ^[16] En el siglo XII, otro matemático persa , Sharaf al-Dīn al-Tūsī (1135-1213), escribió el Al-Muʿādalāt ( Tratado de ecuaciones ), que trataba de ocho tipos de ecuaciones cúbicas con soluciones positivas y cinco tipos de ecuaciones cúbicas que pueden no tener soluciones positivas. Usó lo que más tarde se conocería como el " método Ruffini - Horner " para aproximar numéricamente la raíz de una ecuación cúbica. También utilizó los conceptos de máximos y mínimos de curvas para resolver ecuaciones cúbicas que pueden no tener soluciones positivas. ^[17] Comprendió la importancia del discriminante de la ecuación cúbica para encontrar soluciones algebraicas a ciertos tipos de ecuaciones cúbicas. ^[18]

En su libro Flos , Leonardo de Pisa, también conocido como Fibonacci (1170-1250), pudo aproximar estrechamente la solución positiva de la ecuación cúbica x ³ + 2 x ² + 10 x = 20 . Escribiendo en números babilónicos dio el resultado como 1,22,7,42,33,4,40 (equivalente a 1 + 22/60 + 7/60 ²  + 42/60 ³  + 33/60 ⁴  + 4/60 ⁵  + 40/60 ⁶ ), que tiene un error relativo de aproximadamente 10 ⁻⁹ . ^[19]

A principios del siglo XVI, el matemático italiano Scipione del Ferro (1465-1526) encontró un método para resolver una clase de ecuaciones cúbicas, concretamente aquellas de la forma x ³ + mx = n . De hecho, todas las ecuaciones cúbicas se pueden reducir a esta forma si se permite que m y n sean negativos, pero en ese momento no conocía los números negativos . Del Ferro mantuvo su logro en secreto hasta poco antes de su muerte, cuando se lo contó a su alumno Antonio Fior.

Niccolò Fontana Tartaglia

En 1535, Niccolò Tartaglia (1500-1557) recibió dos problemas de ecuaciones cúbicas de Zuanne da Coi y anunció que podía resolverlos. Pronto fue desafiado por Fior, lo que llevó a una famosa contienda entre los dos. Cada concursante tenía que aportar una determinada cantidad de dinero y proponer una serie de problemas para que los resolviera su rival. Quien resolviera más problemas en 30 días se quedaría con todo el dinero. Tartaglia recibió preguntas de la forma x ³ + mx = n , para las cuales había elaborado un método general. Fior recibió preguntas en la forma x ³ + mx ² = n , que le resultaron demasiado difíciles de resolver, y Tartaglia ganó el concurso.

Más tarde, Gerolamo Cardano (1501-1576) convenció a Tartaglia para que revelara su secreto para resolver ecuaciones cúbicas. En 1539, Tartaglia lo hizo sólo con la condición de que Cardano nunca lo revelara y que, si escribía un libro sobre cúbicas, le daría tiempo a Tartaglia para publicarlo. Algunos años más tarde, Cardano se enteró del trabajo anterior de Del Ferro y publicó el método de Del Ferro en su libro Ars Magna en 1545, lo que significa que Cardano le dio a Tartaglia seis años para publicar sus resultados (con crédito otorgado a Tartaglia por una solución independiente).

La promesa de Cardano a Tartaglia decía que no publicaría el trabajo de Tartaglia, y Cardano sintió que estaba publicando el de Del Ferro para eludir la promesa. Sin embargo, esto llevó a un desafío a Cardano por parte de Tartaglia, que Cardano negó. El desafío fue finalmente aceptado por el alumno de Cardano, Lodovico Ferrari (1522-1565). A Ferrari le fue mejor que a Tartaglia en la competición, y Tartaglia perdió tanto su prestigio como sus ingresos. ^[20]

Cardano notó que el método de Tartaglia a veces requería que extrajera la raíz cuadrada de un número negativo. Incluso incluyó un cálculo con estos números complejos en Ars Magna , pero realmente no lo entendió. Rafael Bombelli estudió esta cuestión en detalle ^[21] y, por lo tanto, a menudo se le considera el descubridor de los números complejos.

François Viète (1540-1603) derivó de forma independiente la solución trigonométrica para la cúbica con tres raíces reales, y René Descartes (1596-1650) amplió el trabajo de Viète. ^[22]

Factorización

Si los coeficientes de una ecuación cúbica son números racionales , se puede obtener una ecuación equivalente con coeficientes enteros, multiplicando todos los coeficientes por un múltiplo común de sus denominadores. tal ecuación

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

con coeficientes enteros, se dice que es reducible si el polinomio del lado izquierdo es el producto de polinomios de grados inferiores. Según el lema de Gauss , si la ecuación es reducible, se puede suponer que los factores tienen coeficientes enteros.

Encontrar las raíces de una ecuación cúbica reducible es más fácil que resolver el caso general. De hecho, si la ecuación es reducible, uno de los factores debe tener grado uno y, por tanto, tener la forma

${\displaystyle qx-p}$

siendo q y p números enteros coprimos . La prueba de la raíz racional permite encontrar q y p examinando un número finito de casos (porque q debe ser un divisor de a y p debe ser un divisor de d ).

Por lo tanto, una raíz es y las otras raíces son las raíces del otro factor, que se puede encontrar mediante división larga polinomial . Este otro factor es ${\displaystyle \textstyle x_{1}={\frac {p}{q}},}$

${\displaystyle {\frac {a}{q}}x^{2}+{\frac {bq+ap}{q^{2}}}x+{\frac {cq^{2}+bpq+ap^{2}}{q^{3}}}}$

(Los coeficientes parecen no ser números enteros, pero deben ser números enteros si p / q es una raíz).

Luego, las otras raíces son las raíces de este polinomio cuadrático y se pueden encontrar usando la fórmula cuadrática .

cúbico deprimido

Cubicos de la forma

${\displaystyle t^{3}+pt+q}$

se dice que están deprimidos. Son mucho más simples que las cúbicas generales, pero son fundamentales, porque el estudio de cualquier cúbica se puede reducir con un simple cambio de variable al de una cúbica deprimida.

Dejar

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

ser una ecuación cúbica. El cambio de variable

${\displaystyle x=t-{\frac {b}{3a}}}$

da una cúbica (en t ) que no tiene término en t ² .

Después de dividir por uno se obtiene la ecuación cúbica deprimida.

${\displaystyle t^{3}+pt+q=0,}$

con

${\displaystyle {\begin{aligned}t={}&x+{\frac {b}{3a}}\\p={}&{\frac {3ac-b^{2}}{3a^{2}}}\\q={}&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}}$

Las raíces de la ecuación original están relacionadas con las raíces de la ecuación deprimida por las relaciones ${\displaystyle x_{1},x_{2},x_{3}}$ ${\displaystyle t_{1},t_{2},t_{3}}$

$${\displaystyle x_{i}=t_{i}-{\frac {b}{3a}},}$$

${\displaystyle i=1,2,3}$

Discriminante y naturaleza de las raíces.

La naturaleza (real o no, distinta o no) de las raíces de una cúbica se puede determinar sin calcularlas explícitamente, utilizando el discriminante .

discriminante

El discriminante de un polinomio es una función de sus coeficientes que es cero si y sólo si el polinomio tiene raíz múltiple , o, si es divisible por el cuadrado de un polinomio no constante. En otras palabras, el discriminante es distinto de cero si y sólo si el polinomio no tiene cuadrados .

Si r ₁ , r ₂ , r ₃ son las tres raíces (no necesariamente distintas ni reales ) de la cúbica entonces el discriminante es ${\displaystyle ax^{3}+bx^{2}+cx+d,}$

${\displaystyle a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}.}$

El discriminante de la cúbica deprimida es ${\displaystyle t^{3}+pt+q}$

${\displaystyle -\left(4\,p^{3}+27\,q^{2}\right).}$

El discriminante de la cúbica general es ${\displaystyle ax^{3}+bx^{2}+cx+d}$

${\displaystyle 18\,abcd-4\,b^{3}d+b^{2}c^{2}-4\,ac^{3}-27\,a^{2}d^{2}.}$

Es el producto y el discriminante de la cúbica deprimida correspondiente. Usando la fórmula que relaciona la cúbica general y la cúbica deprimida asociada, esto implica que el discriminante de la cúbica general se puede escribir como ${\displaystyle a^{4}}$

${\displaystyle {\frac {4(b^{2}-3ac)^{3}-(2b^{3}-9abc+27a^{2}d)^{2}}{27a^{2}}}.}$

Se deduce que uno de estos dos discriminantes es cero si y sólo si el otro también es cero y, si los coeficientes son reales , los dos discriminantes tienen el mismo signo. En resumen, se puede deducir la misma información de cualquiera de estos dos discriminantes.

Para probar las fórmulas anteriores, se pueden usar las fórmulas de Vieta para expresar todo como polinomios en r ₁ , r ₂ , r ₃ y a . La prueba resulta entonces en la verificación de la igualdad de dos polinomios.

Naturaleza de las raíces

Si los coeficientes de un polinomio son números reales , y su discriminante no es cero, se dan dos casos: ${\displaystyle \Delta }$

• Si la cúbica tiene tres raíces reales distintas ${\displaystyle \Delta >0,}$
• Si la cúbica tiene una raíz real y dos raíces conjugadas complejas no reales . ${\displaystyle \Delta <0,}$

Esto se puede probar de la siguiente manera. Primero, si r es una raíz de un polinomio con coeficientes reales, entonces su conjugado complejo también es una raíz. Entonces, las raíces no reales, si las hay, se presentan como pares de raíces conjugadas complejas. Como un polinomio cúbico tiene tres raíces (no necesariamente distintas) según el teorema fundamental del álgebra , al menos una raíz debe ser real.

Como se indicó anteriormente, si r ₁ , r ₂ , r ₃ son las tres raíces de la cúbica , entonces el discriminante es ${\displaystyle ax^{3}+bx^{2}+cx+d}$

${\displaystyle \Delta =a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}}$

Si las tres raíces son reales y distintas, el discriminante es producto de reales positivos, es decir ${\displaystyle \Delta >0.}$

Si sólo una raíz, digamos r ₁ , es real, entonces r ₂ y r ₃ son conjugados complejos, lo que implica que r ₂ – r ₃ es un número puramente imaginario y, por tanto, que ( r ₂ – r ₃ ) ² es real y negativo. Por otro lado, r ₁ – r ₂ y r ₁ – r ₃ son conjugados complejos y su producto es real y positivo. ^[23] Así, el discriminante es el producto de un único número negativo y varios positivos. Eso es ${\displaystyle \Delta <0.}$

raíz múltiple

Si el discriminante de una cúbica es cero, la cúbica tiene raíz múltiple . Si además sus coeficientes son reales, entonces todas sus raíces son reales.

El discriminante de la cúbica deprimida es cero si Si p también es cero, entonces p = q = 0 y 0 es una raíz triple de la cúbica. Si y p ≠ 0 , entonces la cúbica tiene raíz simple ${\displaystyle t^{3}+pt+q}$ ${\displaystyle 4p^{3}+27q^{2}=0.}$ ${\displaystyle 4p^{3}+27q^{2}=0,}$

${\displaystyle t_{1}={\frac {3q}{p}}}$

y una doble raíz

${\displaystyle t_{2}=t_{3}=-{\frac {3q}{2p}}.}$

En otras palabras,

${\displaystyle t^{3}+pt+q=\left(t-{\frac {3q}{p}}\right)\left(t+{\frac {3q}{2p}}\right)^{2}.}$

Este resultado puede demostrarse expandiendo este último producto o recuperarse resolviendo el sistema bastante simple de ecuaciones resultante de las fórmulas de Vieta .

Al utilizar la reducción de una cúbica deprimida, estos resultados se pueden extender a la cúbica general. Esto da: Si el discriminante de la cúbica es cero, entonces ${\displaystyle ax^{3}+bx^{2}+cx+d}$

• tampoco, si la cúbica tiene raíz triple ${\displaystyle b^{2}=3ac,}$

${\displaystyle x_{1}=x_{2}=x_{3}=-{\frac {b}{3a}},}$

y

${\displaystyle ax^{3}+bx^{2}+cx+d=a\left(x+{\frac {b}{3a}}\right)^{3}}$

• o, si la cúbica tiene doble raíz ${\displaystyle b^{2}\neq 3ac,}$

${\displaystyle x_{2}=x_{3}={\frac {9ad-bc}{2(b^{2}-3ac)}},}$

y una raíz simple,

${\displaystyle x_{1}={\frac {4abc-9a^{2}d-b^{3}}{a(b^{2}-3ac)}}.}$

y por lo tanto

${\displaystyle ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})^{2}.}$

Característica 2 y 3

Los resultados anteriores son válidos cuando los coeficientes pertenecen a un campo de característica distinto de 2 o 3, pero deben modificarse para la característica 2 o 3, debido a las divisiones involucradas entre 2 y 3.

La reducción a una cúbica deprimida funciona para la característica 2, pero no para la característica 3. Sin embargo, en ambos casos, es más sencillo establecer y exponer los resultados para la cúbica general. La principal herramienta para ello es el hecho de que una raíz múltiple es una raíz común del polinomio y su derivada formal . En estas características, si la derivada no es una constante, es un polinomio lineal en la característica 3 y es el cuadrado de un polinomio lineal en la característica 2. Por lo tanto, para la característica 2 o 3, la derivada tiene una sola raíz. Esto permite calcular la raíz múltiple, y la raíz tercera se puede deducir de la suma de las raíces, que es proporcionada por las fórmulas de Vieta .

Una diferencia con otras características es que, en la característica 2, la fórmula de una raíz doble involucra una raíz cuadrada y, en la característica 3, la fórmula de una raíz triple involucra una raíz cúbica.

La fórmula de Cardano

A Gerolamo Cardano se le atribuye la publicación de la primera fórmula para resolver ecuaciones cúbicas, atribuyéndola a Scipione del Ferro y Niccolo Fontana Tartaglia . La fórmula se aplica a las cúbicas deprimidas, pero, como se muestra en § Cúbica deprimida, permite resolver todas las ecuaciones cúbicas.

El resultado de Cardano es que si

${\displaystyle t^{3}+pt+q=0}$

es una ecuación cúbica tal que p y q son números reales tales que es positiva (esto implica que el discriminante de la ecuación es negativo) entonces la ecuación tiene raíz real ${\displaystyle \Delta ={\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}$

${\displaystyle {\sqrt[{3}]{u_{1}}}+{\sqrt[{3}]{u_{2}}},}$

donde y son los dos números y ${\displaystyle u_{1}}$ ${\displaystyle u_{2}}$ ${\displaystyle -{\frac {q}{2}}+{\sqrt {\Delta }}}$ ${\displaystyle -{\frac {q}{2}}-{\sqrt {\Delta }}.}$

Consulte § Derivación de las raíces, a continuación, para conocer varios métodos para obtener este resultado.

Como se muestra en § Naturaleza de las raíces, las otras dos raíces son números conjugados complejos no reales , en este caso. Más tarde se demostró (Cardano no sabía números complejos ) que las otras dos raíces se obtienen multiplicando una de las raíces cúbicas por la raíz cúbica primitiva de la unidad y la otra raíz cúbica por la otra raíz cúbica primitiva de la unidad . Es decir, las otras raíces de la ecuación son y ^[24] ${\displaystyle \varepsilon _{1}={\frac {-1+i{\sqrt {3}}}{2}},}$ ${\displaystyle \varepsilon _{2}=\varepsilon _{1}^{2}={\frac {-1-i{\sqrt {3}}}{2}}.}$ ${\displaystyle \varepsilon _{1}{\sqrt[{3}]{u_{1}}}+\varepsilon _{2}{\sqrt[{3}]{u_{2}}}}$ ${\displaystyle \varepsilon _{2}{\sqrt[{3}]{u_{1}}}+\varepsilon _{1}{\sqrt[{3}]{u_{2}}}.}$

Si hay tres raíces reales, pero la teoría de Galois permite demostrar que, si no hay una raíz racional, las raíces no pueden expresarse mediante una expresión algebraica que involucre únicamente números reales. Por tanto, la ecuación no se puede resolver en este caso con el conocimiento de la época de Cardano. Por eso este caso ha sido llamado casus irreducibilis , que significa caso irreductible en latín. ${\displaystyle 4p^{3}+27q^{2}<0,}$

En casus irreducibilis , todavía se puede utilizar la fórmula de Cardano, pero se necesita cierto cuidado en el uso de raíces cúbicas. Un primer método consiste en definir los símbolos y como representantes de los valores principales de la función raíz (es decir, la raíz que tiene la parte real más grande). Con esta convención, la fórmula de Cardano para las tres raíces sigue siendo válida, pero no es puramente algebraica, como la definición de parte principal no es puramente algebraica, ya que implica desigualdades para comparar partes reales. Además, el uso de la raíz cúbica principal puede dar un resultado incorrecto si los coeficientes son números complejos no reales. Además, si los coeficientes pertenecen a otro campo , la raíz cúbica principal no está definida en general. ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$

La segunda forma de hacer que la fórmula de Cardano sea siempre correcta es observar que el producto de las dos raíces cúbicas debe ser –p / 3 . Resulta que una raíz de la ecuación es

${\displaystyle C-{\frac {p}{3C}}\quad {\text{with}}\quad C={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

En esta fórmula, los símbolos y denotan cualquier raíz cuadrada y cualquier raíz cúbica. Las otras raíces de la ecuación se obtienen cambiando la raíz cúbica o, de manera equivalente, multiplicando la raíz cúbica por una raíz cúbica primitiva de la unidad, es decir ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ ${\displaystyle \textstyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

Esta fórmula para las raíces siempre es correcta excepto cuando p = q = 0 , con la condición de que si p = 0 , se elige la raíz cuadrada de modo que C ≠ 0 . Sin embargo, la fórmula es inútil en estos casos ya que las raíces se pueden expresar sin raíz cúbica. Del mismo modo, la fórmula también es inútil en los otros casos en los que no se necesita raíz cúbica, es decir, cuando el polinomio cúbico no es irreducible . ${\displaystyle 4p^{3}+27q^{2}=0}$

Esta fórmula también es correcta cuando p y q pertenecen a cualquier campo de característica distinto de 2 o 3.

Fórmula cúbica general

Una fórmula cúbica para las raíces de la ecuación cúbica general (con a ≠ 0 )

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

se puede deducir de cada variante de la fórmula de Cardano mediante reducción a una cúbica deprimida. La variante que aquí se presenta es válida no sólo para coeficientes reales, sino también para coeficientes a , b , c , d pertenecientes a cualquier campo de característica distinto de 2 o 3.

Como la fórmula es bastante complicada, vale la pena dividirla en fórmulas más pequeñas.

Dejar

${\displaystyle {\begin{aligned}\Delta _{0}&=b^{2}-3ac,\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d.\end{aligned}}}$

(Ambos y se pueden expresar como resultantes de la cúbica y sus derivadas: es ${\displaystyle \Delta _{0}}$ ${\displaystyle \Delta _{1}}$ ${\displaystyle \Delta _{1}}$−1/8 unmultiplicado por la resultante de la cúbica y su segunda derivada, y es ${\displaystyle \Delta _{0}}$−1/12a _veces la resultante de la primera y segunda derivada del polinomio cúbico.)

Entonces deja

${\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},}$

donde los símbolos y se interpretan como cualquier raíz cuadrada y cualquier raíz cúbica, respectivamente (cada número complejo distinto de cero tiene dos raíces cuadradas y tres raíces cúbicas). El signo " ± " antes de la raíz cuadrada es " + " o " – "; la elección es casi arbitraria y cambiarla equivale a elegir una raíz cuadrada diferente. Sin embargo, si una elección produce C = 0 (esto ocurre si ), entonces se debe seleccionar el otro signo. Si ambas opciones dan C = 0 , es decir, si una fracción ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ ${\displaystyle \Delta _{0}=0}$ ${\displaystyle \Delta _{0}=\Delta _{1}=0,}$0/0ocurre en las siguientes fórmulas; esta fracción debe interpretarse como igual a cero (ver el final de esta sección). Con estas convenciones, una de las raíces es

${\displaystyle x=-{\frac {1}{3a}}\left(b+C+{\frac {\Delta _{0}}{C}}\right){\text{.}}}$

Las otras dos raíces se pueden obtener cambiando la elección de la raíz cúbica en la definición de C , o, de manera equivalente, multiplicando C por una raíz cúbica primitiva de la unidad , es decir–1 ± √ –3/2. En otras palabras, las tres raíces son

${\displaystyle x_{k}=-{\frac {1}{3a}}\left(b+\xi ^{k}C+{\frac {\Delta _{0}}{\xi ^{k}C}}\right),\qquad k\in \{0,1,2\}{\text{,}}}$

donde ξ =–1 + √ –3/2.

En cuanto al caso especial de una cúbica deprimida, se aplica esta fórmula, pero es inútil cuando las raíces se pueden expresar sin raíces cúbicas. En particular, si la fórmula da que las tres raíces son iguales , significa que el polinomio cúbico se puede factorizar como Un cálculo sencillo permite verificar que la existencia de esta factorización es equivalente a ${\displaystyle \Delta _{0}=\Delta _{1}=0,}$ ${\displaystyle {\frac {-b}{3a}},}$ ${\displaystyle \textstyle a(x+{\frac {b}{3a}})^{3}.}$ ${\displaystyle \Delta _{0}=\Delta _{1}=0.}$

Soluciones trigonométricas e hiperbólicas.

Solución trigonométrica para tres raíces reales.

Cuando una ecuación cúbica con coeficientes reales tiene tres raíces reales, las fórmulas que expresan estas raíces en términos de radicales involucran números complejos. La teoría de Galois permite demostrar que cuando las tres raíces son reales, y ninguna es racional ( casus irreducibilis ), no se pueden expresar las raíces en términos de radicales reales. Sin embargo, se pueden obtener expresiones puramente reales de las soluciones utilizando funciones trigonométricas , concretamente en términos de cosenos y arcocosenos . ^[25] Más precisamente, las raíces de la cúbica deprimida

${\displaystyle t^{3}+pt+q=0}$

son ^[26]

${\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[\,{\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,\right)-{\frac {2\pi k}{3}}\,\right]\qquad {\text{for }}k=0,1,2.}$

Esta fórmula se debe a François Viète . ^[22] Es puramente real cuando la ecuación tiene tres raíces reales (es decir ). De lo contrario, sigue siendo correcto, pero involucra cosenos y arcocosenos complejos cuando solo hay una raíz real, y no tiene sentido (división por cero) cuando p = 0 . ${\displaystyle 4p^{3}+27q^{2}<0}$

Esta fórmula se puede transformar directamente en una fórmula para las raíces de una ecuación cúbica general, utilizando la sustitución hacia atrás descrita en § Cúbica deprimida.

La fórmula se puede demostrar de la siguiente manera: Partiendo de la ecuación t ³ + pt + q = 0 , establezcamos t = u cos  θ . La idea es elegir u para que la ecuación coincida con la identidad 

${\displaystyle 4\cos ^{3}\theta -3\cos \theta -\cos(3\theta )=0.}$

Para esto, elija y divida la ecuación por Esto da ${\displaystyle u=2\,{\sqrt {-{\frac {p}{3}}}}\,,}$ ${\displaystyle {\frac {u^{3}}{4}}.}$

${\displaystyle 4\cos ^{3}\theta -3\cos \theta -{\frac {3q}{2p}}\,{\sqrt {\frac {-3}{p}}}=0.}$

Combinando con la identidad anterior, se obtiene

${\displaystyle \cos(3\theta )={\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,,}$

y las raíces son así

${\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[{\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right]\qquad {\text{for }}k=0,1,2.}$

Solución hiperbólica para una raíz real

Cuando solo hay una raíz real (y p ≠ 0 ), esta raíz se puede representar de manera similar usando funciones hiperbólicas , como ^{[27] [28]}

${\displaystyle {\begin{aligned}t_{0}&=-2{\frac {|q|}{q}}{\sqrt {-{\frac {p}{3}}}}\cosh \left[{\frac {1}{3}}\operatorname {arcosh} \left({\frac {-3|q|}{2p}}{\sqrt {\frac {-3}{p}}}\right)\right]\qquad {\text{if }}~4p^{3}+27q^{2}>0~{\text{ and }}~p<0,\\t_{0}&=-2{\sqrt {\frac {p}{3}}}\sinh \left[{\frac {1}{3}}\operatorname {arsinh} \left({\frac {3q}{2p}}{\sqrt {\frac {3}{p}}}\right)\right]\qquad {\text{if }}~p>0.\end{aligned}}}$

Si p ≠ 0 y las desigualdades de la derecha no se satisfacen (el caso de tres raíces reales), las fórmulas siguen siendo válidas pero involucran cantidades complejas.

Cuando p = ±3 , los valores anteriores de t ₀ a veces se denominan raíz cúbica de Chebyshev. ^[29] Más precisamente, los valores que involucran cosenos y cosenos hiperbólicos definen, cuando p = −3 , la misma función analítica denotada C _1/3 ( q ) , que es la raíz cúbica propia de Chebyshev. El valor que involucra senos hiperbólicos se denota de manera similar S _1/3 ( q ) , cuando p = 3 .

Soluciones geométricas

La solución de Omar Khayyám

Solución geométrica de Omar Khayyám de una ecuación cúbica, para el caso m = 2 , n = 16 , dando la raíz 2 . La intersección de la línea vertical en el eje x en el centro del círculo es una casualidad del ejemplo ilustrado.

Para resolver la ecuación cúbica x ³ + m ² x = n donde n > 0 , Omar Khayyám construyó la parábola y = x ² / m , la circunferencia que tiene como diámetro el segmento [0, n / m ² ] sobre el eje x positivo y una línea vertical que pasa por el punto donde el círculo y la parábola se cruzan sobre el eje x . La solución viene dada por la longitud del segmento de línea horizontal desde el origen hasta la intersección de la línea vertical y el eje x (ver figura).

Una prueba moderna simple es la siguiente. Multiplicar la ecuación por x / m ² y reagrupar los términos da

${\displaystyle {\frac {x^{4}}{m^{2}}}=x\left({\frac {n}{m^{2}}}-x\right).}$

El lado izquierdo es el valor de y ² en la parábola. La ecuación del círculo es y ² + x ( x −norte/metros ²) = 0 , el lado derecho es el valor de y ² en el círculo.

Solución con trisector de ángulo.

Una ecuación cúbica con coeficientes reales se puede resolver geométricamente usando compás, regla y un trisector de ángulos si y solo si tiene tres raíces reales. ^{[30] : Thm. 1}

Una ecuación cúbica se puede resolver mediante construcción con compás y regla (sin trisector) si y sólo si tiene una raíz racional . Esto implica que los viejos problemas de la trisección de ángulos y la duplicación del cubo , planteados por los antiguos matemáticos griegos , no pueden resolverse mediante la construcción con compás y regla.

Interpretación geométrica de las raíces.

Tres raíces reales

Para el cúbico ( 1 ) con tres raíces reales, las raíces son la proyección sobre el eje x de los vértices A , B y C de un triángulo equilátero . El centro del triángulo tiene la misma coordenada x que el punto de inflexión .

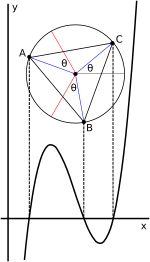
La expresión trigonométrica de Viète de las raíces en el caso de tres raíces reales se presta a una interpretación geométrica en términos de un círculo. ^{[22] [31]} Cuando la cúbica se escribe en forma deprimida ( 2 ) , t ³ + pt + q = 0 , como se muestra arriba, la solución se puede expresar como

${\displaystyle t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.}$

Aquí hay un ángulo en el círculo unitario; tomando ${\displaystyle \arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)}$1/3de ese ángulo corresponde a sacar la raíz cúbica de un número complejo; sumando − k2 π/3para k = 1, 2 encuentra las otras raíces cúbicas; y multiplicar los cosenos de estos ángulos resultantes por correcciones de escala. ${\displaystyle 2{\sqrt {-{\frac {p}{3}}}}}$

Para el caso no deprimido ( 1 ) (que se muestra en el gráfico adjunto), el caso deprimido como se indicó anteriormente se obtiene definiendo t tal que x = t −b/3a _entonces t = x +b/3a _. Gráficamente esto corresponde a simplemente desplazar el gráfico horizontalmente al cambiar entre las variables t y x , sin cambiar las relaciones de los ángulos. Este cambio mueve el punto de inflexión y el centro del círculo hacia el eje y . En consecuencia, las raíces de la ecuación en t suman cero.

Una raíz real

En el plano cartesiano

La pendiente de la línea RA es el doble que la de RH. Denotando las raíces complejas de la cúbica como g ± hi , g = OM (aquí negativo) y h = √ tan ORH = √ pendiente de la recta RH = BE = DA .

Cuando la gráfica de una función cúbica se traza en el plano cartesiano , si solo hay una raíz real, es la abscisa ( coordenada x ) de la intersección horizontal de la curva (punto R en la figura). Además, ^{[32] [33] [34]} si las raíces conjugadas complejas se escriben como g ± hi , entonces la parte real g es la abscisa del punto de tangencia H de la recta tangente a la cúbica que pasa por la intersección x R de el cúbico (es decir, la longitud con signo OM, negativa en la figura). Las partes imaginarias ±h son las raíces cuadradas de la tangente del ángulo entre esta tangente y el eje horizontal. ^{[ se necesita aclaración ]}

En el plano complejo

Con una raíz real y dos complejas, las tres raíces se pueden representar como puntos en el plano complejo, al igual que las dos raíces de la derivada cúbica. Existe una interesante relación geométrica entre todas estas raíces.

Los puntos en el plano complejo que representan las tres raíces sirven como vértices de un triángulo isósceles. (El triángulo es isósceles porque una raíz está en el eje horizontal (real) y las otras dos raíces, al ser conjugadas complejas, aparecen simétricamente por encima y por debajo del eje real.) El teorema de Marden dice que los puntos que representan las raíces de la derivada de la cúbicos son los focos de la inelipse de Steiner del triángulo, la única elipse que es tangente al triángulo en los puntos medios de sus lados. Si el ángulo en el vértice del eje real es menor queπ/3entonces el eje mayor de la elipse se encuentra en el eje real, al igual que sus focos y, por tanto, las raíces de la derivada. Si ese ángulo es mayor queπ/3, el eje mayor es vertical y sus focos, las raíces de la derivada, son conjugados complejos. Y si ese ángulo esπ/3, el triángulo es equilátero, la inelipse de Steiner es simplemente la circunferencia del triángulo, sus focos coinciden entre sí en el incentro, que se encuentra en el eje real y, por tanto, la derivada tiene raíces reales duplicadas.

grupo galois

Dado un polinomio cúbico irreducible sobre un campo K de característica diferente de 2 y 3, el grupo de Galois sobre K es el grupo de automorfismos de campo que fijan K de la extensión más pequeña de K ( campo de división ). Como estos automorfismos deben permutar las raíces de los polinomios, este grupo es el grupo S ₃ de las seis permutaciones de las tres raíces o el grupo A ₃ de las tres permutaciones circulares.

El discriminante Δ de la cúbica es el cuadrado de

${\displaystyle {\sqrt {\Delta }}=a^{2}(r_{1}-r_{2})(r_{1}-r_{3})(r_{2}-r_{3}),}$

donde a es el coeficiente principal de la cúbica y r ₁ , r ₂ y r ₃ son las tres raíces de la cúbica. Como cambios de signo si se intercambian dos raíces, queda fijado por el grupo de Galois sólo si el grupo de Galois es A ₃ . En otras palabras, el grupo de Galois es A ₃ si y sólo si el discriminante es el cuadrado de un elemento de K. ${\displaystyle {\sqrt {\Delta }}}$ ${\displaystyle {\sqrt {\Delta }}}$

Como la mayoría de los números enteros no son cuadrados, cuando se trabaja sobre el campo Q de los números racionales , el grupo de Galois de la mayoría de los polinomios cúbicos irreducibles es el grupo S ₃ con seis elementos. Un ejemplo de un grupo de Galois A ₃ con tres elementos viene dado por p ( x ) = x ³ − 3 x − 1 , cuyo discriminante es 81 = 9 ² .

Derivación de las raíces

Esta sección reagrupa varios métodos para derivar la fórmula de Cardano.

El método de Cardano.

Este método se debe a Scipione del Ferro y Tartaglia , pero lleva el nombre de Gerolamo Cardano quien lo publicó por primera vez en su libro Ars Magna (1545).

Este método se aplica a una cúbica deprimida t ³ + pt + q = 0 . La idea es introducir dos variables u y v tales que u + v = t y sustituir esto en la cúbica deprimida, dando

${\displaystyle u^{3}+v^{3}+(3uv+p)(u+v)+q=0.}$

En este punto Cardano impuso la condición 3uv + p = 0 . Esto elimina el tercer término de la igualdad anterior, lo que lleva al sistema de ecuaciones

${\displaystyle {\begin{aligned}u^{3}+v^{3}&=-q\\uv&=-{\frac {p}{3}}.\end{aligned}}}$

Conociendo la suma y el producto de u ³ y v ³ , se deduce que son las dos soluciones de la ecuación cuadrática

${\displaystyle {\begin{aligned}0&=(x-u^{3})(x-v^{3})\\&=x^{2}-(u^{3}+v^{3})x+u^{3}v^{3}\\&=x^{2}-(u^{3}+v^{3})x+(uv)^{3}\end{aligned}}}$

entonces

${\displaystyle x^{2}+qx-{\frac {p^{3}}{27}}=0.}$

El discriminante de esta ecuación es , y suponiendo que sea positivo, las soluciones reales de esta ecuación son (después de sumar la división por 4 bajo la raíz cuadrada): ${\displaystyle \Delta =q^{2}+{\frac {4p^{3}}{27}}}$

${\displaystyle -{\frac {q}{2}}\pm {\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}.}$

Entonces (sin pérdida de generalidad al elegir u o v ):

${\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

${\displaystyle v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Como u + v = t , la suma de las raíces cúbicas de estas soluciones es una raíz de la ecuación. Eso es

${\displaystyle t={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}}$

es una raíz de la ecuación; esta es la fórmula de Cardano.

Esto funciona bien cuando , pero, si la raíz cuadrada que aparece en la fórmula no es real. Como un número complejo tiene tres raíces cúbicas, usar la fórmula de Cardano sin cuidado proporcionaría nueve raíces, mientras que una ecuación cúbica no puede tener más de tres raíces. Esto fue aclarado por primera vez por Rafael Bombelli en su libro L'Algebra (1572). La solución es utilizar el hecho de que uv = ${\displaystyle 4p^{3}+27q^{2}>0,}$ ${\displaystyle 4p^{3}+27q^{2}<0,}$- pag/3, es decir v =- pag/3 tu. Esto significa que solo es necesario calcular una raíz cúbica y conduce a la segunda fórmula dada en § Fórmula de Cardano.

Las otras raíces de la ecuación se pueden obtener cambiando la raíz cúbica o, de manera equivalente, multiplicando la raíz cúbica por cada una de las dos raíces cúbicas primitivas de la unidad , que son ${\displaystyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

La sustitución de Vieta

La sustitución de Vieta es un método introducido por François Viète (Vieta es su nombre en latín) en un texto publicado póstumamente en 1615, que proporciona directamente la segunda fórmula del método de § Cardano y evita el problema de calcular dos raíces cúbicas diferentes. ^[35]

A partir de la cúbica deprimida t ³ + pt + q = 0 , la sustitución de Vieta es t = w –pag/3 semanas. ^[b]

La sustitución t = w –pag/3 semanastransforma la cúbica deprimida en

${\displaystyle w^{3}+q-{\frac {p^{3}}{27w^{3}}}=0.}$

Multiplicando por w ³ , se obtiene una ecuación cuadrática en w ³ :

${\displaystyle (w^{3})^{2}+q(w^{3})-{\frac {p^{3}}{27}}=0.}$

Dejar

${\displaystyle W=-{\frac {q}{2}}\pm {\sqrt {{\frac {p^{3}}{27}}+{\frac {q^{2}}{4}}}}}$

Sea cualquier raíz distinta de cero de esta ecuación cuadrática. Si w ₁ , w ₂ y w ₃ son las tres raíces cúbicas de W , entonces las raíces del cubo deprimido original son w ₁ −pag/3w ₁ _, w ₂ −pag/3w ₂ _, y w ₃ −pag/3 w ₃. La otra raíz de la ecuación cuadrática es. Esto implica que cambiar el signo de la raíz cuadrada intercambia wi _y − ${\displaystyle \textstyle -{\frac {p^{3}}{27W}}.}$pag/3 con _yopara i = 1, 2, 3 y por lo tanto no cambia las raíces. Este método sólo falla cuando ambas raíces de la ecuación cuadrática son cero, es decir, cuando p = q = 0 , en cuyo caso la única raíz de la ecuación cúbica deprimida es 0 .

método de lagrange

En su artículo Réflexions sur la résolution algébrique des équations ("Reflexiones sobre la resolución algebraica de ecuaciones"), ^[36] Joseph Louis Lagrange introdujo un nuevo método para resolver ecuaciones de bajo grado de manera uniforme, con la esperanza de poder generalizar. para grados superiores. Este método funciona bien para ecuaciones cúbicas y cuárticas , pero Lagrange no logró aplicarlo a una ecuación quíntica , porque requiere resolver un polinomio resolutivo de grado al menos seis. ^{[37] [38] [39]} Aparte del hecho de que nadie lo había logrado anteriormente, este fue el primer indicio de la inexistencia de una fórmula algebraica para los grados 5 y superiores; como lo demostró más tarde el teorema de Abel-Ruffini . Sin embargo, los métodos modernos para resolver ecuaciones quínticas resolubles se basan principalmente en el método de Lagrange. ^[39]

En el caso de ecuaciones cúbicas, el método de Lagrange da la misma solución que el de Cardano. El método de Lagrange se puede aplicar directamente a la ecuación cúbica general ax ³ + bx ² + cx + d = 0 , pero el cálculo es más sencillo con la ecuación cúbica deprimida, t ³ + pt + q = 0 .

La idea principal de Lagrange era trabajar con la transformada discreta de Fourier de las raíces en lugar de con las raíces mismas. Más precisamente, sea ξ una tercera raíz primitiva de la unidad , es decir, un número tal que ξ ³ = 1 y ξ ² + ξ + 1 = 0 (cuando se trabaja en el espacio de números complejos , se tiene , pero esta interpretación compleja no es utilizado aquí). Denotando x ₀ , x ₁ y x ₂ las tres raíces de la ecuación cúbica a resolver, sea ${\displaystyle \textstyle \xi ={\frac {-1\pm i{\sqrt {3}}}{2}}=e^{2i\pi /3},}$

${\displaystyle {\begin{aligned}s_{0}&=x_{0}+x_{1}+x_{2},\\s_{1}&=x_{0}+\xi x_{1}+\xi ^{2}x_{2},\\s_{2}&=x_{0}+\xi ^{2}x_{1}+\xi x_{2},\end{aligned}}}$

Sea la transformada discreta de Fourier de las raíces. Si se conocen s ₀ , s ₁ y s _{2 se pueden recuperar las raíces de los mismos con la transformada inversa de Fourier que consiste en invertir esta transformación lineal;} eso es,

${\displaystyle {\begin{aligned}x_{0}&={\tfrac {1}{3}}(s_{0}+s_{1}+s_{2}),\\x_{1}&={\tfrac {1}{3}}(s_{0}+\xi ^{2}s_{1}+\xi s_{2}),\\x_{2}&={\tfrac {1}{3}}(s_{0}+\xi s_{1}+\xi ^{2}s_{2}).\end{aligned}}}$

Según las fórmulas de Vieta , se sabe que s ₀ es cero en el caso de una cúbica deprimida, y −b/apara la cúbica general. Por lo tanto, sólo es necesario calcular s ₁ y s _{2 .} No son funciones simétricas de las raíces (al intercambiar x ₁ y x ₂ se intercambia también s ₁ y s ₂ ), pero algunas funciones simétricas simples de s ₁ y s ₂ también son simétricas en las raíces de la ecuación cúbica a resolver. Por lo tanto, estas funciones simétricas se pueden expresar en términos de los coeficientes (conocidos) de la cúbica original, y esto permite eventualmente expresar los s _i como raíces de un polinomio con coeficientes conocidos. Esto funciona bien para todos los grados, pero, en grados superiores a cuatro, el polinomio resultante que tiene s i _como raíces tiene un grado mayor que el del polinomio inicial y, por lo tanto, no es útil para resolver. Esta es la razón por la cual el método de Lagrange falla en grados cinco y superiores.

En el caso de una ecuación cúbica, y son polinomios simétricos (ver más abajo). De ello se deduce que y son las dos raíces de la ecuación cuadrática. Por lo tanto, la resolución de la ecuación puede finalizarse exactamente como con el método de Cardano, con y en lugar de u y v . ${\displaystyle P=s_{1}s_{2},}$ ${\displaystyle S=s_{1}^{3}+s_{2}^{3}}$ ${\displaystyle s_{1}^{3}}$ ${\displaystyle s_{2}^{3}}$ ${\displaystyle z^{2}-Sz+P^{3}=0.}$ ${\displaystyle s_{1}}$ ${\displaystyle s_{2}}$

En el caso de la cúbica deprimida, se tiene y mientras que en el método de Cardano hemos establecido y Por lo tanto, hasta el intercambio de u y v , tenemos y En otras palabras, en este caso, el método de Cardano y el método de Lagrange calculan exactamente lo mismo cosas, hasta un factor de tres en las variables auxiliares, siendo la principal diferencia que el método de Lagrange explica por qué aparecen estas variables auxiliares en el problema. ${\displaystyle x_{0}={\tfrac {1}{3}}(s_{1}+s_{2})}$ ${\displaystyle s_{1}s_{2}=-3p,}$ ${\displaystyle x_{0}=u+v}$ ${\displaystyle uv={\tfrac {1}{3}}p.}$ ${\displaystyle s_{1}=3u}$ ${\displaystyle s_{2}=3v.}$

Cálculo de S y P

Un cálculo sencillo utilizando las relaciones ξ ³ = 1 y ξ ² + ξ + 1 = 0 da

${\displaystyle {\begin{aligned}P&=s_{1}s_{2}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-(x_{0}x_{1}+x_{1}x_{2}+x_{2}x_{0}),\\S&=s_{1}^{3}+s_{2}^{3}=2(x_{0}^{3}+x_{1}^{3}+x_{2}^{3})-3(x_{0}^{2}x_{1}+x_{1}^{2}x_{2}+x_{2}^{2}x_{0}+x_{0}x_{1}^{2}+x_{1}x_{2}^{2}+x_{2}x_{0}^{2})+12x_{0}x_{1}x_{2}.\end{aligned}}}$

Esto muestra que P y S son funciones simétricas de las raíces. Utilizando las identidades de Newton , es sencillo expresarlas en términos de funciones simétricas elementales de las raíces, dando

${\displaystyle {\begin{aligned}P&=e_{1}^{2}-3e_{2},\\S&=2e_{1}^{3}-9e_{1}e_{2}+27e_{3},\end{aligned}}}$

con e ₁ = 0 , e ₂ = p y e ₃ = − q en el caso de una cúbica deprimida, y e ₁ = −b/a, mi ₂ =C/ay mi ₃ = −d/a, en el caso general.

Aplicaciones

Las ecuaciones cúbicas surgen en varios otros contextos.

En matemáticas

• La trisección de ángulos y la duplicación del cubo son dos antiguos problemas de geometría que se ha demostrado que no se pueden resolver mediante la construcción con regla y compás , porque equivalen a resolver una ecuación cúbica.
• El teorema de Marden establece que los focos de la elipse de Steiner de cualquier triángulo se pueden encontrar usando la función cúbica cuyas raíces son las coordenadas en el plano complejo de los tres vértices del triángulo. Las raíces de la primera derivada de esta cúbica son las coordenadas complejas de esos focos.
• El área de un heptágono regular se puede expresar en términos de las raíces de un cubo. Además, las razones de la diagonal larga al lado, del lado a la diagonal corta y del negativo de la diagonal corta a la diagonal larga satisfacen una ecuación cúbica particular. Además, la relación entre el inradio y el circunradio de un triángulo heptagonal es una de las soluciones de una ecuación cúbica. Los valores de funciones trigonométricas de ángulos relacionados para satisfacer ecuaciones cúbicas. ${\displaystyle 2\pi /7}$
• Dado el coseno (u otra función trigonométrica) de un ángulo arbitrario, el coseno de un tercio de ese ángulo es una de las raíces de un cúbico.
• La solución de la ecuación cuartica general depende de la solución de su resolutivo cúbico .
• Los valores propios de una matriz de 3×3 son las raíces de un polinomio cúbico que es el polinomio característico de la matriz.
• La ecuación característica de coeficientes constantes de tercer orden o ecuación diferencial lineal o ecuación en diferencias de Cauchy-Euler (coeficientes variables equidimensionales) es una ecuación cúbica.
• Los puntos de intersección de la curva de Bézier cúbica y la línea recta se pueden calcular utilizando una ecuación cúbica directa que representa la curva de Bézier.
• Los puntos críticos de una función cuártica se encuentran resolviendo una ecuación cúbica (la derivada igual a cero).
• Los puntos de inflexión de una función quíntica son la solución de una ecuación cúbica (la segunda derivada igual a cero).

en otras ciencias

• En química analítica , la ecuación de Charlot , que puede usarse para encontrar el pH de soluciones tampón , se puede resolver usando una ecuación cúbica.
• En termodinámica , las ecuaciones de estado (que relacionan la presión, el volumen y la temperatura de una sustancia), por ejemplo, la ecuación de estado de Van der Waals , son cúbicas en volumen.
• Las ecuaciones cinemáticas que involucran velocidades lineales de aceleración son cúbicas.
• La velocidad de las ondas sísmicas de Rayleigh es una solución de la ecuación cúbica de las ondas de Rayleigh .
• La velocidad en estado estacionario de un vehículo que se mueve sobre una pendiente con fricción del aire para una potencia de entrada dada se resuelve mediante una ecuación cúbica deprimida.
• La tercera ley del movimiento planetario de Kepler es cúbica en el semieje mayor.

Notas

1. En O'Connor, John J.; Robertson, Edmund F. , "Omar Khayyam", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrewsse puede leer Este problema, a su vez, llevó a Khayyam a resolver la ecuación cúbica x ³ + 200 x = 20 x ² + 2000 y encontró una raíz positiva de esta cúbica considerando la intersección de una hipérbola rectangular y un círculo. Luego se encontró una solución numérica aproximada mediante interpolación en tablas trigonométricas . La construcción geométrica era perfectamente adecuada para Omar Khayyam, ya que se trata de resolver un problema de construcción geométrica. Al final de su artículo sólo dice que, para este problema geométrico, si las aproximaciones son suficientes, entonces se puede obtener una solución más sencilla consultando tablas trigonométricas . Textualmente: Si el buscador está satisfecho con una estimación, le corresponde consultar la tabla de acordes de Almagesto, o la tabla de senos y senos versados ​​del Observatorio Mothmed. A esto le sigue una breve descripción de este método alternativo (siete líneas).
2. Más precisamente, Vieta introdujo una nueva variable w e impuso la condición w ( t + w ) =pag/3. Esto es equivalente a la sustitución t =pag/3 semanas– w , y difiere de la sustitución que se utiliza aquí sólo por un cambio de signo de w . Este cambio de signo permite obtener directamente las fórmulas de § Fórmula de Cardano.

Referencias

1. Høyrup, Jens (1992), "Retraducción y análisis del texto del sótano de Babilonia BM 85200 + VAT 6599", Ánfora: Festschrift para Hans Wussing con motivo de su 65 cumpleaños , Birkhäuser , págs. 315–358, doi :10.1007/978 -3-0348-8599-7_16, ISBN 978-3-0348-8599-7
2. Crossley, John; WC. Lun, Anthony (1999). Los nueve capítulos sobre el arte matemático: acompañamiento y comentario. Prensa de la Universidad de Oxford. pag. 176.ISBN _ 978-0-19-853936-0.
3. Van der Waerden, Geometría y álgebra de civilizaciones antiguas, capítulo 4, Zurich 1983 ISBN 0-387-12159-5 
4. Cooke, Roger (8 de noviembre de 2012). La Historia de las Matemáticas. John Wiley e hijos. pag. 63.ISBN _ 978-1-118-46029-0.
5. Nemet-Nejat, Karen Rhea (1998). La vida cotidiana en la antigua Mesopotamia . Grupo editorial Greenwood. pag. 306.ISBN _ 978-0-313-29497-6.
6. Cooke, Roger (2008). Álgebra clásica: su naturaleza, orígenes y usos. John Wiley e hijos. pag. 64.ISBN _ 978-0-470-27797-3.
7. Guilbeau (1930, p. 8) afirma que "los egipcios consideraban imposible la solución, pero los griegos se acercaron más a ella".
8. Guilbeau (1930, págs. 8-9)
9. Heath, Thomas L. (30 de abril de 2009). Diofanto de Alejandría: un estudio de la historia del álgebra griega. Pub Martín. págs. 87–91. ISBN 978-1578987542.
10. Arquímedes (8 de octubre de 2007). Las obras de Arquímedes . Traducción de TL Heath. Impresión de borradores. ISBN 978-1603860512.
11. Mikami, Yoshio (1974) [1913], "Capítulo 8 Wang Hsiao-Tung y ecuaciones cúbicas", El desarrollo de las matemáticas en China y Japón (2ª ed.), Nueva York: Chelsea Publishing Co., págs. 53–56 , ISBN 978-0-8284-0149-4
12. Un artículo de Omar Khayyam, Scripta Math. 26 (1963), páginas 323–337
13. JJ O'Connor y EF Robertson (1999), Omar Khayyam, archivo MacTutor History of Mathematics , afirma: "El propio Khayyam parece haber sido el primero en concebir una teoría general de ecuaciones cúbicas".
14. Guilbeau (1930, p. 9) afirma: "Omar Al Hay de Chorassan, alrededor de 1079 d.C., hizo todo lo posible para elevar a método la solución de las ecuaciones algebraicas mediante cónicas que se cruzan".
15. Berggren, JL (18 de enero de 2017). Episodios de las matemáticas del Islam medieval. Saltador. ISBN 978-1-4939-3780-6.
16. Datta, Bibhutibhushan ; Singh, Avadhesh Narayan (2004), "Ecuación de grado superior", Historia de las matemáticas hindúes: un libro de consulta , vol. 2, Delhi, India: Bharattya Kala Prakashan, pág. 76, ISBN 81-86050-86-8
17. O'Connor, John J.; Robertson, Edmund F. , "Sharaf al-Din al-Muzaffar al-Tusi", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
18. Berggren, JL (1990), "Innovación y tradición en Muʿādalāt de Sharaf al-Dīn al-Ṭūsī", Revista de la Sociedad Oriental Americana , 110 (2): 304–309, doi :10.2307/604533, JSTOR  604533
19. O'Connor, John J.; Robertson, Edmund F. , "Fibonacci", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
20. Katz, Víctor (2004). Una historia de las matemáticas. Boston: Addison Wesley. pag. 220.ISBN _ 9780321016188.
21. La Nave, Federica; Mazur, Barry (2002), "Reading Bombelli", The Mathematical Intelligencer , 24 (1): 12–21, doi :10.1007/BF03025306, S2CID  189888034
22. Nickalls, RWD (julio de 2006). "Viète, Descartes y la ecuación cúbica" (PDF) . Gaceta Matemática . 90 (518): 203–208. doi :10.1017/S0025557200179598. S2CID  124980170.
23. Pratt, Orson (1866). Método nuevo y sencillo de solución de ecuaciones cúbicas y bicuadráticas: adoptando varias fórmulas nuevas, simplificando enormemente este departamento de ciencias matemáticas. Longmans, Green, Reader y Dyer. pag. 13.ISBN _ 9781974130924. ...si dos raíces son imaginarias, el producto es positivo...
24. "Solución para una ecuación cúbica deprimida". Solución matemática . Consultado el 23 de noviembre de 2022 .
25. Zucker, IJ (julio de 2008). "La ecuación cúbica: una nueva mirada al caso irreducible". Gaceta Matemática . 92 : 264–268. doi :10.1017/S0025557200183135. S2CID  125986006.
26. Shelbey, Samuel, ed. (1975). Tablas matemáticas estándar CRC. Prensa CRC. ISBN 0-87819-622-6.
27. Estas son las fórmulas (80) y (83) de Weisstein, Eric W. 'Cubic Formula'. De MathWorld: un recurso web de Wolfram. http://mathworld.wolfram.com/CubicFormula.html, reescrito para tener una notación coherente.
28. Holmes, GC, "El uso de cosenos hiperbólicos en la resolución de polinomios cúbicos", Mathematical Gazette 86. Noviembre de 2002, 473–477.
29. Abramowitz, Milton; Stegun, Irene A., eds. Manual de funciones matemáticas con fórmulas, gráficas y tablas matemáticas , Dover (1965), cap. 22p. 773
30. Gleason, Andrew Mattei (marzo de 1988). "Trisección de ángulos, el heptágono y el triskaidecágono" (PDF) . El Mensual Matemático Estadounidense . 95 (3): 185-194. doi :10.2307/2323624. JSTOR  2323624. Archivado desde el original (PDF) el 19 de diciembre de 2015.
31. Nickalls, RWD (noviembre de 1993), "Un nuevo enfoque para resolver la cúbica: se revela la solución de Cardan" (PDF) , The Mathematical Gazette , 77 (480): 354–359, doi :10.2307/3619777, ISSN  0025-5572, JSTOR  3619777, S2CID  172730765Ver especialmente Figura 2.
32. Henriquez, García (junio-julio de 1935), "La interpretación gráfica de las raíces complejas de ecuaciones cúbicas", American Mathematical Monthly , 42 (6): 383–384, doi :10.2307/2301359, JSTOR  2301359
33. Barr, CF (1918), "Discusiones: relacionadas con la gráfica de una ecuación cúbica que tiene raíces complejas", American Mathematical Monthly , 25 (6): 268–269, doi :10.2307/2972885, JSTOR  2972885
34. Irwin, franco; Wright, HN (1917), "Algunas propiedades de las curvas polinomiales", Annals of Mathematics , 19 (2): 152–158, doi :10.2307/1967772, JSTOR  1967772
35. van der Waerden, Bartel Leenert (1985), "De Viète a Descartes", Una historia del álgebra: de al-Khwārizmī a Emmy Noether , Springer-Verlag , ISBN 3-540-13610-X
36. Lagrange, Joseph-Louis (1869) [1771], "Réflexions sur la résolution algébrique des équations", en Serret, Joseph-Alfred (ed.), Œuvres de Lagrange , vol. III, Gauthier-Villars, págs. 205–421
37. Prasolov, Víktor; Solovyev, Yuri (1997), Funciones elípticas e integrales elípticas, Librería AMS, ISBN 978-0-8218-0587-9, §6.2, pág. 134
38. Kline, Morris (1990), Pensamiento matemático desde la antigüedad hasta los tiempos modernos, Oxford University Press EE. UU., ISBN 978-0-19-506136-9, Álgebra en el siglo XVIII: la teoría de las ecuaciones
39. Daniel Lazard, "Resolver quinticas en radicales", en Olav Arnfinn Laudal, Ragni Piene , The Legacy of Niels Henrik Abel , págs. 207-225, Berlín, 2004. ISBN 3-540-43826-2 

Referencias

• Guilbeau, Lucye (1930), "La historia de la solución de la ecuación cúbica", Mathematics News Letter , 5 (4): 8–12, doi :10.2307/3027812, JSTOR  3027812

Otras lecturas

• Anglin, WS; Lambek, Joachim (1995), "Matemáticas en el Renacimiento", La herencia de Tales , Springers, págs. 125-131, ISBN 978-0-387-94544-6Cap. 24.
• Dence, T. (noviembre de 1997), "Cúbicos, caos y método de Newton", Mathematical Gazette , Mathematical Association , 81 (492): 403–408, doi :10.2307/3619617, ISSN  0025-5572, JSTOR  3619617, S2CID  125196796
• Dunnett, R. (noviembre de 1994), "Newton-Raphson and the cubic", Mathematical Gazette , Mathematical Association , 78 (483): 347–348, doi :10.2307/3620218, ISSN  0025-5572, JSTOR  3620218, S2CID  125643035
• Jacobson, Nathan (2009), Álgebra básica , vol. 1 (2ª ed.), Dover, ISBN 978-0-486-47189-1
• Mitchell, DW (noviembre de 2007), "Resolver cúbicas resolviendo triángulos", Mathematical Gazette , Mathematical Association , 91 : 514–516, doi :10.1017/S0025557200182178, ISSN  0025-5572, S2CID  124710259
• Mitchell, DW (noviembre de 2009), "Potencias de φ como raíces de cúbicas", Mathematical Gazette , Mathematical Association , 93 , doi :10.1017/S0025557200185237, ISSN  0025-5572, S2CID  126286653
• Prensa, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 5.6 Ecuaciones cuadráticas y cúbicas", Recetas numéricas: el arte de la informática científica (3.ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-521-88068-8
• Rechtschaffen, Edgar (julio de 2008), "Raíces reales de cúbicas: fórmula explícita para cuasi-soluciones", Mathematical Gazette , Mathematical Association , 92 : 268–276 , doi :10.1017/S0025557200183147, ISSN  0025-5572, S2CID  125870578
• Zucker, IJ (julio de 2008), "La ecuación cúbica: una nueva mirada al caso irreducible", Mathematical Gazette , Mathematical Association , 92 : 264–268, doi :10.1017/S0025557200183135, ISSN  0025-5572, S2CID  125986006

enlaces externos

• "Fórmula Cardano", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Historia de las ecuaciones cuadráticas, cúbicas y cuárticas en el archivo MacTutor .
• 500 años de NO enseñar LA FÓRMULA CÚBICA. ¿Qué es lo que creen que no puedes manejar? – Vídeo de YouTube de Mathologer sobre la historia de las ecuaciones cúbicas y la solución de Cardano, así como la solución de Ferrari a las ecuaciones de cuarto grado.