Teoría de la relatividad

Hay que indicar que las leyes del movimiento de Newton son un caso particular de esta teoría donde la masa, al viajar a velocidades muy pequeñas, no experimenta variación alguna en longitud ni se transforma en energía y al tiempo se le puede considerar absoluto.

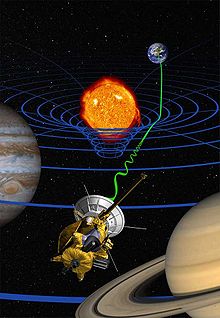
La teoría de la relatividad general, publicada en 1915, es una teoría de la gravedad que reemplaza a la gravedad newtoniana, aunque coincide numéricamente con ella para campos gravitatorios débiles y velocidades «pequeñas».

Anteriormente, a la interacción gravitatoria se la describía matemáticamente por medio de una distribución de masas, pero en esta teoría no solo la masa percibe esta interacción, sino también la energía, mediante la curvatura del espacio-tiempo y por eso se necesita otro lenguaje matemático para poder describirla, el cálculo tensorial.

La relatividad general también abrió otro campo de investigación en la física, conocido como cosmología y es ampliamente utilizado en la astrofísica.

Esta teoría describe correctamente el movimiento de los cuerpos incluso a grandes velocidades y sus interacciones electromagnéticas, se usa básicamente para estudiar sistemas de referencia inerciales (no es aplicable para problemas astrofísicos donde el campo gravitatorio desempeña un papel importante).

Estos conceptos fueron presentados anteriormente por Poincaré y Lorentz, que son considerados como precursores de la teoría.

Además, dada una curva arbitraria en el espacio-tiempo, puede definirse a lo largo de ella el llamado intervalo relativista, que se obtiene a partir del tensor métrico.

A su vez un campo dependiendo de su naturaleza puede representarse por un escalar, un vector o un tensor.

Por ejemplo el campo electromagnético se representa por un tensor de segundo orden totalmente antisimétrico o 2-forma.

En este contexto se dice que una magnitud es un invariante relativista si tiene el mismo valor para todos los observadores, obviamente todos los invariantes relativistas son escalares (0-tensores), frecuentemente formados por la contracción de magnitudes tensoriales.

El tensor métrico del espacio-tiempo plano de Minkowski se designa con la letra

Como el lector habrá podido comprobar, los intervalos nulos son aquellos que corresponden a partículas que se mueven a la velocidad de la luz, como los fotones: La distancia

, es decir, el intervalo es igual al tiempo local multiplicado por la velocidad de la luz.

Esta invarianza se expresa a través de la llamada geometría hiperbólica: La ecuación del intervalo

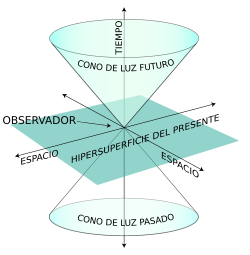
En el espacio-tiempo de Minkowski, las propiedades cinemáticas de las partículas se representan fundamentalmente por tres magnitudes: La cuadrivelocidad (o tetravelocidad), la cuadriaceleración y el cuadrimomentum (o tetramomentum).

), o lo que es lo mismo, a la velocidad de la luz c. Para partículas sin masa, como los fotones, el procedimiento anterior no se puede aplicar, y la cuadrivelocidad puede definirse simplemente como vector tangente a la trayectoria seguida por los mismos.

Su magnitud es igual a cero en los sistemas inerciales, cuyas líneas del mundo son geodésicas, rectas en el espacio-tiempo llano de Minkowski.

) multiplicada por la velocidad (en este caso, la cuadrivelocidad), y por lo tanto sus componentes son los siguientes:

El momentum conservado, al igual que el intervalo y la cuadrivelocidad propia, permanece invariante ante las transformaciones de coordenadas, aunque también aquí hay que distinguir entre los cuerpos con masa y los fotones.

En los primeros, la magnitud del cuadriomentum es igual a la masa multiplicada por la velocidad de la luz

Los primeros sostenían, siguiendo a Descartes y Huygens, que la magnitud conservada en todo movimiento venía constituida por el momentum total del sistema, mientras que los energetistas —que tomaban por base los estudios de Leibniz— consideraban que la magnitud conservada venía conformada por la suma de dos cantidades: La fuerza viva, equivalente a la mitad de la masa multiplicada por la velocidad al cuadrado (

Tres son las ecuaciones fundamentales que en física newtoniana describen el fenómeno de la gravitación universal: la primera, afirma que la fuerza gravitatoria entre dos cuerpos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de su distancia (1); la segunda, que el potencial gravitatorio (

) en un determinado punto es igual a la masa multiplicada por la constante G y dividida por la distancia r (2); y la tercera, finalmente, es la llamada ecuación de Poisson (3), que indica que el laplaciano[nota 5]​ del potencial gravitatorio es igual a

Sin embargo, estas ecuaciones no son compatibles con la Relatividad Especial por dos razones: Por todo ello, resulta necesario prescindir del término

Además, si los componentes del tensor se miden por un observador en reposo relativo respecto al fluido, entonces, el tensor métrico viene constituido simplemente por la métrica de Minkowski: Puesto que además la tetravelocidad del fluido respecto al observador en reposo es: como consecuencia de ello, los coeficientes del tensor de tensión-energía son los siguientes:

Podemos, a partir del tensor de tensión-energía, calcular cuánta masa contiene un determinado volumen del fluido: Retomando la definición de este tensor expuesta unas líneas más arriba, se puede definir al coeficiente

es aquella región que se define por las tres bases vectoriales normales al vector

es aquella región del espacio-tiempo definida por los tres vectores unitarios normales a

Las ecuaciones deducidas por el físico escocés James Clerk Maxwell demostraron que electricidad y magnetismo no son más que dos manifestaciones de un mismo fenómeno físico: el campo electromagnético.

Ahora bien, para describir las propiedades de este campo los físicos de finales del siglo XIX debían utilizar dos vectores diferentes, los correspondientes los campos eléctrico y magnético.