En matemáticas , un espacio es un conjunto (a veces denominado universo ) dotado de una estructura que define las relaciones entre los elementos del conjunto. Un subespacio es un subconjunto del espacio original que conserva la misma estructura. Si bien las matemáticas modernas utilizan muchos tipos de espacios, como los espacios euclidianos , los espacios lineales , los espacios topológicos , los espacios de Hilbert o los espacios de probabilidad , no definen la noción de "espacio" en sí. [1] [a]

Un espacio consiste en objetos matemáticos seleccionados que se tratan como puntos y relaciones seleccionadas entre estos puntos. La naturaleza de los puntos puede variar ampliamente: por ejemplo, los puntos pueden representar números, funciones en otro espacio o subespacios de otro espacio. Son las relaciones las que definen la naturaleza del espacio. Más precisamente, los espacios isomorfos se consideran idénticos, donde un isomorfismo entre dos espacios es una correspondencia uno a uno entre sus puntos que preserva las relaciones. Por ejemplo, las relaciones entre los puntos de un espacio euclidiano tridimensional están determinadas de manera única por los axiomas de Euclides, [b] y todos los espacios euclidianos tridimensionales se consideran idénticos.
Las nociones topológicas como la continuidad tienen definiciones naturales para cada espacio euclidiano. Sin embargo, la topología no distingue entre líneas rectas y líneas curvas, y la relación entre los espacios euclidianos y topológicos es, por tanto, "olvidable". Relaciones de este tipo se tratan con más detalle en la sección "Tipos de espacios".
No siempre está claro si un objeto matemático dado debe considerarse un "espacio" geométrico o una "estructura" algebraica . Una definición general de "estructura", propuesta por Bourbaki [2] , abarca todos los tipos comunes de espacios, proporciona una definición general de isomorfismo y justifica la transferencia de propiedades entre estructuras isomorfas.

En las matemáticas de la antigua Grecia, el "espacio" era una abstracción geométrica de la realidad tridimensional que se observa en la vida cotidiana. Alrededor del año 300 a. C., Euclides formuló axiomas para las propiedades del espacio. Euclides construyó toda la matemática sobre estos fundamentos geométricos, llegando incluso a definir los números comparando las longitudes de los segmentos de línea con la longitud de un segmento de referencia elegido.
El método de coordenadas ( geometría analítica ) fue adoptado por René Descartes en 1637. [3] En esa época, los teoremas geométricos eran tratados como verdades objetivas absolutas cognoscibles a través de la intuición y la razón, similares a los objetos de las ciencias naturales; [4] : 11 y los axiomas eran tratados como implicaciones obvias de las definiciones. [4] : 15
Se utilizaron dos relaciones de equivalencia entre figuras geométricas: congruencia y semejanza . Las traslaciones, rotaciones y reflexiones transforman una figura en figuras congruentes; las homotecias , en figuras semejantes. Por ejemplo, todos los círculos son mutuamente semejantes, pero las elipses no son semejantes a los círculos. Una tercera relación de equivalencia, introducida por Gaspard Monge en 1795, se da en geometría proyectiva : no sólo las elipses, sino también las parábolas e hipérbolas, se convierten en círculos bajo transformaciones proyectivas apropiadas; todas son figuras proyectivamente equivalentes.
La relación entre las dos geometrías, la euclidiana y la proyectiva, [4] : 133 muestra que los objetos matemáticos no nos son dados con su estructura . [4] : 21 Más bien, cada teoría matemática describe sus objetos por algunas de sus propiedades, precisamente aquellas que se ponen como axiomas en los fundamentos de la teoría. [4] : 20
Las distancias y los ángulos no pueden aparecer en los teoremas de la geometría proyectiva, ya que estos conceptos no se mencionan en los axiomas de la geometría proyectiva ni se definen a partir de los conceptos mencionados en ellos. La pregunta "¿cuál es la suma de los tres ángulos de un triángulo?" tiene sentido en la geometría euclidiana, pero carece de sentido en la geometría proyectiva.
En el siglo XIX se produjo una situación diferente: en algunas geometrías la suma de los tres ángulos de un triángulo está bien definida pero es diferente del valor clásico (180 grados). La geometría hiperbólica no euclidiana , introducida por Nikolai Lobachevsky en 1829 y János Bolyai en 1832 (y Carl Friedrich Gauss en 1816, inédito) [4] : 133 afirmó que la suma depende del triángulo y siempre es menor que 180 grados. Eugenio Beltrami en 1868 y Felix Klein en 1871 obtuvieron "modelos" euclidianos de la geometría hiperbólica no euclidiana, y con ello justificaron completamente esta teoría como una posibilidad lógica. [4] : 24 [5]
Este descubrimiento obligó a abandonar las pretensiones de verdad absoluta de la geometría euclidiana. Demostró que los axiomas no son "evidencias" ni "implicaciones de definiciones". Más bien, son hipótesis. ¿En qué medida corresponden a una realidad experimental? Este importante problema físico ya no tiene nada que ver con las matemáticas. Incluso si una "geometría" no corresponde a una realidad experimental, sus teoremas no dejan de ser "verdades matemáticas". [4] : 15
Un modelo euclidiano de una geometría no euclidiana es una elección de algunos objetos existentes en el espacio euclidiano y algunas relaciones entre estos objetos que satisfacen todos los axiomas (y por lo tanto, todos los teoremas) de la geometría no euclidiana. Estos objetos y relaciones euclidianos "representan" la geometría no euclidiana como actores contemporáneos que representan una representación antigua. Los actores pueden imitar una situación que nunca ocurrió en la realidad. Las relaciones entre los actores en el escenario imitan las relaciones entre los personajes de la obra. Del mismo modo, las relaciones elegidas entre los objetos elegidos del modelo euclidiano imitan las relaciones no euclidianas. Esto demuestra que las relaciones entre objetos son esenciales en matemáticas, mientras que la naturaleza de los objetos no lo es.
La palabra "geometría" (del griego antiguo: geo- "tierra", -metron "medición") inicialmente significaba una forma práctica de procesar longitudes, regiones y volúmenes en el espacio en que vivimos, pero luego se extendió ampliamente (al igual que la noción de espacio en cuestión aquí).
Según Bourbaki, [4] : 131 el período entre 1795 ( Géométrie descriptive de Monge) y 1872 (el "programa de Erlangen" de Klein) puede ser llamado "la edad de oro de la geometría". El espacio original investigado por Euclides es ahora llamado espacio euclidiano tridimensional . Su axiomatización, iniciada por Euclides hace 23 siglos, fue reformada con los axiomas de Hilbert , los axiomas de Tarski y los axiomas de Birkhoff . Estos sistemas axiomáticos describen el espacio a través de nociones primitivas (como "punto", "entre", "congruente") limitadas por un número de axiomas .
La geometría analítica hizo grandes progresos y logró reemplazar los teoremas de la geometría clásica por cálculos mediante invariantes de grupos de transformación. [4] : 134, 5 Desde entonces, los nuevos teoremas de la geometría clásica han sido de más interés para los aficionados que para los matemáticos profesionales. [4] : 136 Sin embargo, la herencia de la geometría clásica no se perdió. Según Bourbaki, [4] : 138 "pasada por alto en su papel como ciencia autónoma y viva, la geometría clásica se transfigura así en un lenguaje universal de las matemáticas contemporáneas".
Simultáneamente, los números comenzaron a desplazar a la geometría como fundamento de las matemáticas. Por ejemplo, en el ensayo de 1872 de Richard Dedekind Stetigkeit und irrationale Zahlen ( Continuidad y números irracionales ), afirma que los puntos de una línea deben tener las propiedades de los cortes de Dedekind y que, por lo tanto, una línea es lo mismo que el conjunto de números reales. Dedekind es cuidadoso al señalar que se trata de una suposición que no se puede demostrar. En los tratamientos modernos, la afirmación de Dedekind se toma a menudo como la definición de una línea, reduciendo así la geometría a la aritmética. El espacio euclidiano tridimensional se define como un espacio afín cuyo espacio vectorial asociado de diferencias de sus elementos está equipado con un producto interno. [6] Una definición "desde cero", como en Euclides, ya no se utiliza a menudo, ya que no revela la relación de este espacio con otros espacios. Además, un espacio proyectivo tridimensional se define ahora como el espacio de todos los subespacios unidimensionales (es decir, líneas rectas que pasan por el origen) de un espacio vectorial cuatridimensional. Este cambio de fundamentos requiere un nuevo conjunto de axiomas y, si se adoptan, los axiomas clásicos de la geometría se convierten en teoremas.
Un espacio ahora consta de objetos matemáticos seleccionados (por ejemplo, funciones en otro espacio, o subespacios de otro espacio, o simplemente elementos de un conjunto) tratados como puntos, y relaciones seleccionadas entre estos puntos. Por lo tanto, los espacios son simplemente estructuras matemáticas de conveniencia. Uno podría esperar que las estructuras llamadas "espacios" se perciban de manera más geométrica que otros objetos matemáticos, pero esto no siempre es cierto.
Según la famosa conferencia inaugural pronunciada por Bernhard Riemann en 1854, todo objeto matemático parametrizado por n números reales puede ser tratado como un punto del espacio n -dimensional de todos esos objetos. [4] : 140 Los matemáticos contemporáneos siguen esta idea rutinariamente y encuentran extremadamente sugerente utilizar la terminología de la geometría clásica casi en todas partes. [4] : 138
Las funciones son objetos matemáticos importantes. Normalmente forman espacios de funciones de dimensión infinita , como ya señaló Riemann [4] : 141 y se elaboró en el siglo XX mediante el análisis funcional .
Aunque cada tipo de espacio tiene su propia definición, la idea general de "espacio" escapa a la formalización. Algunas estructuras se denominan espacios y otras no, sin un criterio formal. Además, no hay consenso sobre la idea general de "estructura". Según Pudlák, [7] "Las matemáticas [...] no pueden explicarse completamente mediante un único concepto como la estructura matemática. Sin embargo, el enfoque estructuralista de Bourbaki es el mejor que tenemos". Volveremos al enfoque estructuralista de Bourbaki en la última sección "Espacios y estructuras", mientras que ahora esbozamos una posible clasificación de los espacios (y de las estructuras) en el espíritu de Bourbaki.
Clasificamos los espacios en tres niveles. Dado que cada teoría matemática describe sus objetos por algunas de sus propiedades, la primera pregunta que debemos hacernos es: ¿cuáles propiedades? Esto nos lleva al primer nivel de clasificación (superior). En el segundo nivel, se tienen en cuenta las respuestas a preguntas especialmente importantes (entre las preguntas que tienen sentido según el primer nivel). En el tercer nivel de clasificación, se tienen en cuenta las respuestas a todas las preguntas posibles.
Por ejemplo, la clasificación de nivel superior distingue entre espacios euclidianos y proyectivos , ya que la distancia entre dos puntos está definida en los espacios euclidianos pero no está definida en los espacios proyectivos. Otro ejemplo. La pregunta "¿cuál es la suma de los tres ángulos de un triángulo?" tiene sentido en un espacio euclidiano pero no en un espacio proyectivo. En un espacio no euclidiano la pregunta tiene sentido pero se responde de manera diferente, lo que no es una distinción de nivel superior.
Además, la distinción entre un plano euclidiano y un espacio tridimensional euclidiano no es una distinción de nivel superior; la pregunta "¿cuál es la dimensión?" tiene sentido en ambos casos.
La clasificación de segundo nivel distingue, por ejemplo, entre espacios euclidianos y no euclidianos; entre espacios de dimensión finita y de dimensión infinita; entre espacios compactos y no compactos, etc. En términos de Bourbaki, [2] la clasificación de segundo nivel es la clasificación por “especies”. A diferencia de la taxonomía biológica, un espacio puede pertenecer a varias especies.
La clasificación de tercer nivel distingue, por ejemplo, entre espacios de diferente dimensión, pero no distingue entre un plano de un espacio euclidiano tridimensional, tratado como un espacio euclidiano bidimensional, y el conjunto de todos los pares de números reales, también tratado como un espacio euclidiano bidimensional. Asimismo, no distingue entre diferentes modelos euclidianos del mismo espacio no euclidiano. Más formalmente, el tercer nivel clasifica los espacios hasta el isomorfismo . Un isomorfismo entre dos espacios se define como una correspondencia biunívoca entre los puntos del primer espacio y los puntos del segundo espacio, que conserva todas las relaciones estipuladas según el primer nivel. Los espacios mutuamente isomorfos se consideran copias de un único espacio. Si uno de ellos pertenece a una especie dada, entonces todos lo hacen.
La noción de isomorfismo arroja luz sobre la clasificación de nivel superior. Dada una correspondencia biunívoca entre dos espacios de la misma clase de nivel superior, uno puede preguntarse si se trata de un isomorfismo o no. Esta pregunta no tiene sentido para dos espacios de clases diferentes.
Un isomorfismo consigo mismo se denomina automorfismo. Los automorfismos de un espacio euclidiano son desplazamientos, rotaciones, reflexiones y composiciones de estos. El espacio euclidiano es homogéneo en el sentido de que cada punto puede transformarse en cualquier otro punto mediante algún automorfismo.
Los axiomas euclidianos [b] no dejan libertad; determinan de manera única todas las propiedades geométricas del espacio. Más exactamente: todos los espacios euclidianos tridimensionales son mutuamente isomorfos. En este sentido tenemos "el" espacio euclidiano tridimensional. En términos de Bourbaki, la teoría correspondiente es univalente . En contraste, los espacios topológicos son generalmente no isomorfos; su teoría es multivalente . Una idea similar ocurre en la lógica matemática: una teoría se llama categórica si todos sus modelos de la misma cardinalidad son mutuamente isomorfos. Según Bourbaki, [8] el estudio de las teorías multivalentes es la característica más llamativa que distingue las matemáticas modernas de las matemáticas clásicas.
Las nociones topológicas (continuidad, convergencia, conjuntos abiertos, conjuntos cerrados, etc.) se definen de forma natural en cada espacio euclidiano. En otras palabras, cada espacio euclidiano es también un espacio topológico. Todo isomorfismo entre dos espacios euclidianos es también un isomorfismo entre los espacios topológicos correspondientes (llamado " homeomorfismo "), pero lo inverso es erróneo: un homeomorfismo puede distorsionar las distancias. En términos de Bourbaki [2] , el "espacio topológico" es una estructura subyacente a la estructura del "espacio euclidiano". Ideas similares aparecen en la teoría de categorías : la categoría de los espacios euclidianos es una categoría concreta sobre la categoría de los espacios topológicos; el funtor olvidadizo (o "despojador") asigna la primera categoría a la segunda.
Un espacio euclidiano tridimensional es un caso especial de espacio euclidiano. En términos de Bourbaki, [2] la especie del espacio euclidiano tridimensional es más rica que la especie del espacio euclidiano. Asimismo, la especie del espacio topológico compacto es más rica que la especie del espacio topológico.
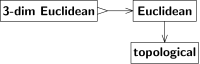
Tales relaciones entre especies de espacios pueden expresarse diagramáticamente como se muestra en la Fig. 3. Una flecha de A a B significa que cada espacio A es también un espacio B, o puede ser tratado como un espacio B, o proporciona un espacio B, etc. Tratando A y B como clases de espacios uno puede interpretar la flecha como una transición de A a B. (En términos de Bourbaki, [9] "procedimiento de deducción" de un espacio B a partir de un espacio A. No exactamente una función a menos que las clases A, B sean conjuntos; este matiz no invalida lo siguiente.) Las dos flechas en la Fig. 3 no son invertibles, pero por diferentes razones.
La transición de "euclidiano" a "topológico" es olvidadiza. La topología distingue entre continuo y discontinuo, pero no entre rectilíneo y curvilíneo. La intuición nos dice que la estructura euclidiana no puede restaurarse a partir de la topología. Una demostración utiliza un automorfismo del espacio topológico (es decir, un autohomeomorfismo ) que no es un automorfismo del espacio euclidiano (es decir, no es una composición de desplazamientos, rotaciones y reflexiones). Tal transformación convierte la estructura euclidiana dada en una estructura euclidiana (isomorfa pero) diferente; ambas estructuras euclidianas corresponden a una única estructura topológica.
En cambio, la transición de "euclidiano tridimensional" a "euclidiano" no es olvidable; un espacio euclidiano no necesita ser tridimensional, pero si resulta ser tridimensional, es completo, no se pierde ninguna estructura. En otras palabras, la última transición es inyectiva (uno a uno), mientras que la primera no lo es (muchos a uno). Denotamos las transiciones inyectivas con una flecha con una cola dentada, "↣" en lugar de "→".
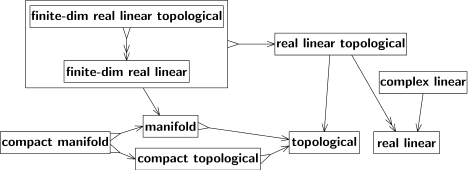
Ambas transiciones no son sobreyectivas , es decir, no todo B-espacio resulta de algún A-espacio. En primer lugar, un espacio euclidiano tridimensional es un caso especial (no general) de un espacio euclidiano. En segundo lugar, una topología de un espacio euclidiano es un caso especial de topología (por ejemplo, debe ser no compacto y conexo, etc.). Denotamos las transiciones sobreyectivas con una flecha de dos puntas, "↠" en lugar de "→". Véase, por ejemplo, la figura 4; allí, la flecha de "topológico lineal real" a "lineal real" tiene dos puntas, ya que todo espacio lineal real admite alguna (al menos una) topología compatible con su estructura lineal.
En general, esta topología no es única, pero sí lo es cuando el espacio lineal real es de dimensión finita. Para estos espacios, la transición es tanto inyectiva como sobreyectiva, es decir, biyectiva ; véase la flecha que va de "topología lineal real finita-dim" a "lineal real finita-dim" en la figura 4. La transición inversa existe (y podría mostrarse con una segunda flecha hacia atrás). Por lo tanto, las dos especies de estructuras son equivalentes. En la práctica, no se hace distinción entre especies equivalentes de estructuras. [10] Las estructuras equivalentes pueden tratarse como una única estructura, como se muestra con un gran recuadro en la figura 4.
Las transiciones señaladas por las flechas obedecen a isomorfismos, es decir, dos espacios A isomorfos conducen a dos espacios B isomorfos .
El diagrama de la Fig. 4 es conmutativo . Es decir, todos los caminos dirigidos en el diagrama con los mismos puntos de inicio y fin conducen al mismo resultado. Otros diagramas a continuación también son conmutativos, excepto las flechas discontinuas de la Fig. 9. La flecha de "topológico" a "medible" es discontinua por la razón explicada allí: "Para convertir un espacio topológico en un espacio medible, se le dota de un σ-álgebra. El σ-álgebra de los conjuntos de Borel es la opción más popular, pero no la única". Una flecha sólida denota una transición predominante, llamada "canónica", que se sugiere de forma natural y se utiliza ampliamente, a menudo de forma implícita, por defecto. Por ejemplo, al hablar de una función continua en un espacio euclidiano, no es necesario especificar su topología explícitamente. De hecho, existen topologías alternativas y se utilizan a veces, por ejemplo, la topología fina ; pero estas siempre se especifican explícitamente, ya que son mucho menos notables que la topología predominante. Una flecha discontinua indica que se utilizan varias transiciones y que ninguna es muy frecuente.
Dos espacios básicos son los espacios lineales (también llamados espacios vectoriales) y los espacios topológicos .
Los espacios lineales son de naturaleza algebraica ; hay espacios lineales reales (sobre el cuerpo de los números reales ), espacios lineales complejos (sobre el cuerpo de los números complejos ) y, de manera más general, espacios lineales sobre cualquier cuerpo. Todo espacio lineal complejo es también un espacio lineal real (el último subyace al primero), ya que cada número complejo puede especificarse mediante dos números reales. Por ejemplo, el plano complejo tratado como un espacio lineal complejo unidimensional puede degradarse a un espacio lineal real bidimensional. En contraste, la línea real puede tratarse como un espacio lineal real unidimensional pero no como un espacio lineal complejo. Véase también extensiones de cuerpo . De manera más general, un espacio vectorial sobre un cuerpo también tiene la estructura de un espacio vectorial sobre un subcuerpo de ese cuerpo. Las operaciones lineales, dadas en un espacio lineal por definición, conducen a nociones tales como líneas rectas (y planos, y otros subespacios lineales); líneas paralelas; elipses (y elipsoides). Sin embargo, es imposible definir líneas ortogonales (perpendiculares) o distinguir círculos entre elipses, porque en un espacio lineal no hay una estructura como un producto escalar que pueda usarse para medir ángulos. La dimensión de un espacio lineal se define como el número máximo de vectores linealmente independientes o, equivalentemente, como el número mínimo de vectores que abarcan el espacio; puede ser finito o infinito. Dos espacios lineales sobre el mismo cuerpo son isomorfos si y solo si tienen la misma dimensión. Un espacio lineal complejo n -dimensional es también un espacio lineal real 2n - dimensional .
Los espacios topológicos son de naturaleza analítica . Los conjuntos abiertos , dados en un espacio topológico por definición, conducen a nociones tales como funciones continuas , caminos, aplicaciones; sucesiones convergentes, límites ; interior, frontera, exterior. Sin embargo, la continuidad uniforme , los conjuntos acotados , las sucesiones de Cauchy y las funciones diferenciables (caminos, aplicaciones) permanecen sin definir. Los isomorfismos entre espacios topológicos se denominan tradicionalmente homeomorfismos; estos son correspondencias biunívocas continuas en ambas direcciones. El intervalo abierto (0,1) es homeomorfo a toda la línea real (−∞,∞) pero no homeomorfo al intervalo cerrado [0,1], ni a un círculo. La superficie de un cubo es homeomorfa a una esfera (la superficie de una pelota) pero no homeomorfa a un toro. Los espacios euclidianos de diferentes dimensiones no son homeomorfos, lo que parece evidente, pero no es fácil de demostrar. La dimensión de un espacio topológico es difícil de definir; Se pueden utilizar la dimensión inductiva (basada en la observación de que la dimensión del borde de una figura geométrica suele ser una menos que la dimensión de la propia figura) y la dimensión de recubrimiento de Lebesgue . En el caso de un espacio euclidiano n -dimensional , ambas dimensiones topológicas son iguales a n .
Cada subconjunto de un espacio topológico es en sí mismo un espacio topológico (en contraste, sólo los subconjuntos lineales de un espacio lineal son espacios lineales). Los espacios topológicos arbitrarios, investigados por la topología general (también llamada topología de conjuntos puntuales) son demasiado diversos para una clasificación completa hasta el homeomorfismo. Los espacios topológicos compactos son una clase importante de espacios topológicos ("especies" de este "tipo"). Toda función continua está acotada en dicho espacio. El intervalo cerrado [0,1] y la línea real extendida [−∞,∞] son compactos; el intervalo abierto (0,1) y la línea (−∞,∞) no lo son. La topología geométrica investiga las variedades (otra "especie" de este "tipo"); estos son espacios topológicos localmente homeomorfos a los espacios euclidianos (y que satisfacen algunas condiciones adicionales). Las variedades de baja dimensión se clasifican completamente hasta el homeomorfismo.
Tanto la estructura lineal como la topológica subyacen a la estructura del espacio topológico lineal (en otras palabras, el espacio vectorial topológico). Un espacio topológico lineal es a la vez un espacio lineal real o complejo y un espacio topológico, de modo que las operaciones lineales son continuas. Por lo tanto, un espacio lineal que también es topológico no es, en general, un espacio topológico lineal.
Todo espacio lineal real o complejo de dimensión finita es un espacio topológico lineal en el sentido de que tiene una y sólo una topología que lo convierte en un espacio topológico lineal. Las dos estructuras, "espacio lineal real o complejo de dimensión finita" y "espacio topológico lineal de dimensión finita", son, por tanto, equivalentes, es decir, mutuamente subyacentes. En consecuencia, toda transformación lineal invertible de un espacio topológico lineal de dimensión finita es un homeomorfismo. Las tres nociones de dimensión (una algebraica y dos topológicas) coinciden para los espacios lineales reales de dimensión finita. Sin embargo, en los espacios de dimensión infinita, diferentes topologías pueden ajustarse a una estructura lineal dada, y las transformaciones lineales invertibles generalmente no son homeomorfismos.

Es conveniente introducir espacios afines y proyectivos por medio de espacios lineales, como sigue. Un subespacio lineal n -dimensional de un espacio lineal ( n +1)-dimensional , siendo en sí mismo un espacio lineal n -dimensional , no es homogéneo; contiene un punto especial, el origen. Desplazándolo por un vector externo a él, se obtiene un subespacio afín n -dimensional . Es homogéneo. Un espacio afín no necesita estar incluido en un espacio lineal, pero es isomorfo a un subespacio afín de un espacio lineal. Todos los espacios afines n -dimensionales sobre un cuerpo dado son mutuamente isomorfos. En palabras de John Baez , "un espacio afín es un espacio vectorial que ha olvidado su origen". En particular, todo espacio lineal es también un espacio afín.
Dado un subespacio afín de n dimensiones A en un espacio lineal de ( n + 1) dimensiones L , una línea recta en A puede definirse como la intersección de A con un subespacio lineal bidimensional de L que interseca a A : en otras palabras, con un plano que pasa por el origen y que no es paralelo a A . De manera más general, un subespacio afín de k dimensiones de A es la intersección de A con un subespacio lineal de ( k + 1) dimensiones de L que interseca a A .
Cada punto del subespacio afín A es la intersección de A con un subespacio lineal unidimensional de L . Sin embargo, algunos subespacios unidimensionales de L son paralelos a A ; en cierto sentido, intersecan a A en el infinito. El conjunto de todos los subespacios lineales unidimensionales de un espacio lineal de ( n + 1)-dimensional es, por definición, un espacio proyectivo de n -dimensional . Y el subespacio afín A está incrustado en el espacio proyectivo como un subconjunto propio. Sin embargo, el espacio proyectivo en sí es homogéneo. Una línea recta en el espacio proyectivo corresponde a un subespacio lineal bidimensional del espacio lineal de ( n + 1)-dimensional. De manera más general, un subespacio proyectivo de k -dimensional del espacio proyectivo corresponde a un subespacio lineal de ( k + 1)-dimensional del espacio lineal de ( n + 1)-dimensional, y es isomorfo al espacio proyectivo de k -dimensional .
Definidos de esta manera, los espacios afines y proyectivos son de naturaleza algebraica; pueden ser reales, complejos y, más generalmente, sobre cualquier cuerpo.
Todo espacio afín o proyectivo real o complejo es también un espacio topológico. Un espacio afín es una variedad no compacta; un espacio proyectivo es una variedad compacta. En un espacio proyectivo real una línea recta es homeomorfa a un círculo, por lo tanto compacta, en contraste con una línea recta en un espacio lineal o afín.

Las distancias entre puntos se definen en un espacio métrico . Los isomorfismos entre espacios métricos se denominan isometrías. Todo espacio métrico es también un espacio topológico. Un espacio topológico se denomina metrizable si subyace a un espacio métrico. Todas las variedades son metrizables.
En un espacio métrico, podemos definir conjuntos acotados y sucesiones de Cauchy. Un espacio métrico se denomina completo si todas las sucesiones de Cauchy convergen. Todo espacio incompleto está isométricamente inserto, como un subconjunto denso, en un espacio completo (la completitud). Todo espacio métrico compacto es completo; la recta real no es compacta pero está completa; el intervalo abierto (0,1) es incompleto.
Todo espacio euclidiano es también un espacio métrico completo. Además, todas las nociones geométricas inmanentes a un espacio euclidiano pueden caracterizarse en términos de su métrica. Por ejemplo, el segmento recto que une dos puntos dados A y C está formado por todos los puntos B tales que la distancia entre A y C es igual a la suma de dos distancias, entre A y B y entre B y C.
La dimensión de Hausdorff (relacionada con la cantidad de bolitas que cubren el conjunto dado) se aplica a espacios métricos y puede ser no entera (especialmente para fractales ). Para un espacio euclidiano n -dimensional , la dimensión de Hausdorff es igual a n .
Los espacios uniformes no introducen distancias, pero permiten utilizar continuidad uniforme, sucesiones de Cauchy (o filtros o redes ), completitud y terminación. Todo espacio uniforme es también un espacio topológico. Todo espacio topológico lineal (metrizable o no) es también un espacio uniforme, y es completo en dimensión finita pero generalmente incompleto en dimensión infinita. De manera más general, todo grupo topológico conmutativo es también un espacio uniforme. Un grupo topológico no conmutativo, sin embargo, tiene dos estructuras uniformes, una invariante por la izquierda y la otra invariante por la derecha.

Los vectores en un espacio euclidiano forman un espacio lineal, pero cada vector tiene también una longitud, es decir, una norma, . Un espacio lineal real o complejo dotado de una norma es un espacio normado . Todo espacio normado es a la vez un espacio topológico lineal y un espacio métrico. Un espacio de Banach es un espacio normado completo. Muchos espacios de sucesiones o funciones son espacios de Banach de dimensión infinita.
El conjunto de todos los vectores de norma menor que uno se denomina bola unidad de un espacio normado. Es un conjunto convexo, simétrico centralmente, generalmente no un elipsoide; por ejemplo, puede ser un polígono (en el plano) o, más generalmente, un politopo (en una dimensión finita arbitraria). La ley del paralelogramo (también llamada identidad del paralelogramo)
generalmente falla en espacios normados, pero es válido para vectores en espacios euclidianos, lo que se deduce del hecho de que la norma euclidiana al cuadrado de un vector es su producto interno consigo mismo, .
Un espacio producto interior es un espacio lineal real o complejo, dotado de una forma bilineal o respectivamente sesquilineal, que satisface algunas condiciones y se denomina producto interior. Todo espacio producto interior es también un espacio normado. Un espacio normado subyace a un espacio producto interior si y sólo si satisface la ley del paralelogramo, o equivalentemente, si su bola unidad es un elipsoide. Los ángulos entre vectores se definen en espacios producto interior. Un espacio de Hilbert se define como un espacio producto interior completo. (Algunos autores insisten en que debe ser complejo, otros admiten también espacios de Hilbert reales.) Muchos espacios de sucesiones o funciones son espacios de Hilbert de dimensión infinita. Los espacios de Hilbert son muy importantes para la teoría cuántica . [11]
Todos los espacios producto interior real de n dimensiones son mutuamente isomorfos. Se puede decir que el espacio euclidiano de n dimensiones es el espacio producto interior real de n dimensiones que olvidó su origen.

Las variedades suaves no se denominan "espacios", pero podrían serlo. Toda variedad suave es una variedad topológica y puede estar incluida en un espacio lineal de dimensión finita. Las superficies suaves en un espacio lineal de dimensión finita son variedades suaves: por ejemplo, la superficie de un elipsoide es una variedad suave, un politopo no lo es. Los espacios lineales, afines y proyectivos de dimensión finita reales o complejos también son variedades suaves.
En cada uno de sus puntos, una trayectoria suave en una variedad suave tiene un vector tangente que pertenece al espacio tangente de la variedad en ese punto. Los espacios tangentes a una variedad suave de n dimensiones son espacios lineales de n dimensiones . La diferencial de una función suave en una variedad suave proporciona una función lineal en el espacio tangente en cada punto.
Una variedad de Riemann , o espacio de Riemann, es una variedad suave cuyos espacios tangentes están dotados de productos internos que satisfacen ciertas condiciones. Los espacios euclidianos también son espacios de Riemann. Las superficies suaves en espacios euclidianos son espacios de Riemann. Un espacio hiperbólico no euclidiano también es un espacio de Riemann. Una curva en un espacio de Riemann tiene una longitud, y la longitud de la curva más corta entre dos puntos define una distancia, de modo que el espacio de Riemann es un espacio métrico. El ángulo entre dos curvas que se cortan en un punto es el ángulo entre sus líneas tangentes.
Renunciando a la positividad de los productos internos en los espacios tangentes, se obtienen espacios pseudo-Riemann , incluidos los espacios lorentzianos que son muy importantes para la relatividad general .

Dejando de lado las distancias y los ángulos, pero conservando los volúmenes (de los cuerpos geométricos), se llega a la teoría de la medida . Además del volumen, la medida generaliza las nociones de área, longitud, distribución de masa (o carga) y también distribución de probabilidad, según el enfoque de Andrey Kolmogorov sobre la teoría de la probabilidad .
Un "cuerpo geométrico" de las matemáticas clásicas es mucho más regular que un simple conjunto de puntos. El límite del cuerpo es de volumen cero. Por lo tanto, el volumen del cuerpo es el volumen de su interior, y el interior puede agotarse con una secuencia infinita de cubos. En cambio, el límite de un conjunto arbitrario de puntos puede ser de volumen distinto de cero (un ejemplo: el conjunto de todos los puntos racionales dentro de un cubo dado). La teoría de la medida logró extender la noción de volumen a una vasta clase de conjuntos, los llamados conjuntos medibles . De hecho, los conjuntos no medibles casi nunca aparecen en las aplicaciones.
Los conjuntos medibles, dados en un espacio medible por definición, conducen a funciones y aplicaciones medibles. Para convertir un espacio topológico en un espacio medible, se lo dota de una σ-álgebra. La σ-álgebra de conjuntos de Borel es la opción más popular, pero no la única. ( A veces también se utilizan conjuntos de Baire , conjuntos universalmente medibles , etc.). La topología no está determinada únicamente por la σ-álgebra de Borel; por ejemplo, la topología normativa y la topología débil en un espacio de Hilbert separable conducen a la misma σ-álgebra de Borel . No todas las σ-álgebras son las σ-álgebras de Borel de alguna topología. [c] En realidad, una σ-álgebra puede generarse mediante una colección dada de conjuntos (o funciones) independientemente de cualquier topología. Cada subconjunto de un espacio medible es en sí mismo un espacio medible.
Los espacios medibles estándar (también llamados espacios de Borel estándar ) son especialmente útiles debido a cierta similitud con los espacios compactos (ver EoM). Toda aplicación medible biyectiva entre espacios medibles estándar es un isomorfismo; es decir, la aplicación inversa también es medible. Y una aplicación entre tales espacios es medible si y solo si su gráfico es medible en el espacio del producto. De manera similar, toda aplicación continua biyectiva entre espacios métricos compactos es un homeomorfismo; es decir, la aplicación inversa también es continua. Y una aplicación entre tales espacios es continua si y solo si su gráfico es cerrado en el espacio del producto.
Todo conjunto de Borel en un espacio euclidiano (y, más generalmente, en un espacio métrico separable completo), dotado de la σ-álgebra de Borel, es un espacio medible estándar. Todos los espacios mesurables estándar incontables son mutuamente isomorfos.
Un espacio de medida es un espacio medible dotado de una medida. Un espacio euclidiano con la medida de Lebesgue es un espacio de medida. La teoría de la integración define la integrabilidad y las integrales de funciones mensurables en un espacio de medida.
Los conjuntos de medida 0, llamados conjuntos nulos, son despreciables. Por lo tanto, un "isomorfismo módulo 0" se define como un isomorfismo entre subconjuntos de medida completa (es decir, con complemento despreciable).
Un espacio de probabilidad es un espacio de medida tal que la medida de todo el espacio es igual a 1. El producto de cualquier familia (finita o no) de espacios de probabilidad es un espacio de probabilidad. En cambio, para los espacios de medida en general, solo se define el producto de un número finito de espacios. En consecuencia, hay muchas medidas de probabilidad de dimensión infinita (especialmente, medidas gaussianas ), pero ninguna medida de Lebesgue de dimensión infinita.
Los espacios de probabilidad estándar son especialmente útiles . En un espacio de probabilidad estándar, una esperanza condicional puede tratarse como la integral sobre la medida condicional ( probabilidades condicionales regulares , véase también desintegración de la medida ). Dados dos espacios de probabilidad estándar, cada homomorfismo de sus álgebras de medida es inducido por alguna función que preserva la medida. Cada medida de probabilidad en un espacio medible estándar conduce a un espacio de probabilidad estándar. El producto de una secuencia (finita o no) de espacios de probabilidad estándar es un espacio de probabilidad estándar. Todos los espacios de probabilidad estándar no atómicos son mutuamente isomorfos módulo 0; uno de ellos es el intervalo (0,1) con la medida de Lebesgue.
Estos espacios son menos geométricos. En particular, la idea de dimensión, aplicable (de una forma u otra) a todos los demás espacios, no se aplica a los espacios mensurables, de medida y de probabilidad.
El estudio teórico del cálculo, conocido como análisis matemático , condujo a principios del siglo XX a la consideración de espacios lineales de funciones de valor real o de valor complejo. Los primeros ejemplos de estos fueron los espacios de funciones , cada uno adaptado a su propia clase de problemas. Estos ejemplos compartían muchas características comunes, y estas características pronto se abstrajeron en espacios de Hilbert, espacios de Banach y espacios vectoriales topológicos más generales. Estos fueron un poderoso conjunto de herramientas para la solución de una amplia gama de problemas matemáticos.
La información más detallada la llevaba una clase de espacios llamados álgebras de Banach . Se trata de espacios de Banach junto con una operación de multiplicación continua. Un ejemplo temprano importante fue el álgebra de Banach de funciones medibles esencialmente acotadas en un espacio de medida X. Este conjunto de funciones es un espacio de Banach bajo la adición puntual y la multiplicación escalar. Con la operación de multiplicación puntual, se convierte en un tipo especial de espacio de Banach, uno que ahora se llama álgebra de von Neumann conmutativa . La multiplicación puntual determina una representación de esta álgebra en el espacio de Hilbert de funciones integrables al cuadrado en X. Una observación temprana de John von Neumann fue que esta correspondencia también funcionaba a la inversa: dadas algunas hipótesis técnicas suaves, un álgebra de von Neumann conmutativa junto con una representación en un espacio de Hilbert determina un espacio de medida, y estas dos construcciones (de un álgebra de von Neumann más una representación y de un espacio de medida) son mutuamente inversas.
Von Neumann propuso entonces que las álgebras de von Neumann no conmutativas deberían tener un significado geométrico, al igual que las álgebras de von Neumann conmutativas. Junto con Francis Murray , produjo una clasificación de las álgebras de von Neumann. La construcción integral directa muestra cómo descomponer cualquier álgebra de von Neumann en una colección de álgebras más simples llamadas factores . Von Neumann y Murray clasificaron los factores en tres tipos. El tipo I era casi idéntico al caso conmutativo. Los tipos II y III exhibieron nuevos fenómenos. Un álgebra de von Neumann de tipo II determinó una geometría con la característica peculiar de que la dimensión podría ser cualquier número real no negativo, no solo un entero. Las álgebras de tipo III eran aquellas que no eran ni de tipo I ni de tipo II, y después de varias décadas de esfuerzo, se demostró que estaban estrechamente relacionadas con los factores de tipo II.
Un enfoque ligeramente diferente a la geometría de los espacios funcionales se desarrolló al mismo tiempo que el trabajo de von Neumann y Murray sobre la clasificación de factores. Este enfoque es la teoría de las C*-álgebras . Aquí, el ejemplo motivador es la C*-álgebra , donde X es un espacio topológico de Hausdorff localmente compacto. Por definición, esta es el álgebra de funciones continuas de valor complejo en X que se desvanecen en el infinito (lo que significa vagamente que cuanto más se aleja de un punto elegido, más se acerca la función a cero) con las operaciones de adición y multiplicación puntuales. El teorema de Gelfand-Naimark implicaba que existe una correspondencia entre las C*-álgebras conmutativas y los objetos geométricos: Toda C*-álgebra conmutativa tiene la forma para algún espacio de Hausdorff localmente compacto X. En consecuencia, es posible estudiar los espacios de Hausdorff localmente compactos puramente en términos de C*-álgebras conmutativas. La geometría no conmutativa toma esto como inspiración para el estudio de las C*-álgebras no conmutativas: si existiera algo así como un "espacio no conmutativo X ", entonces sería una C*-álgebra no conmutativa ; si además se aplicara el teorema de Gelfand-Naimark a estos objetos inexistentes, entonces los espacios (conmutativos o no) serían lo mismo que las C*-álgebras; así que, a falta de un enfoque directo para la definición de un espacio no conmutativo, un espacio no conmutativo se define como una C*-álgebra no conmutativa. Muchas herramientas geométricas estándar se pueden reformular en términos de C*-álgebras, y esto proporciona técnicas inspiradas en la geometría para estudiar C*-álgebras no conmutativas .
Ambos ejemplos son ahora casos de un campo llamado geometría no conmutativa . Los ejemplos específicos de álgebras de von Neumann y C*-álgebras se conocen como teoría de la medida no conmutativa y topología no conmutativa, respectivamente. La geometría no conmutativa no es meramente una búsqueda de generalidad por sí misma y no es solo una curiosidad. Los espacios no conmutativos surgen de manera natural, incluso inevitable, a partir de algunas construcciones. Por ejemplo, considere los mosaicos de Penrose no periódicos del plano por cometas y dardos. Es un teorema que, en tal mosaico, cada parche finito de cometas y dardos aparece infinitamente a menudo. Como consecuencia, no hay forma de distinguir dos mosaicos de Penrose mirando una porción finita. Esto hace imposible asignar al conjunto de todos los mosaicos una topología en el sentido tradicional. A pesar de esto, los mosaicos de Penrose determinan un C*-álgebra no conmutativa y, en consecuencia, pueden estudiarse mediante las técnicas de la geometría no conmutativa. Otro ejemplo, de gran interés en el campo de la geometría diferencial , son las foliaciones de variedades. Se trata de formas de dividir la variedad en subvariedades de menor dimensión llamadas hojas , cada una de las cuales es localmente paralela a otras cercanas. El conjunto de todas las hojas se puede convertir en un espacio topológico. Sin embargo, el ejemplo de una rotación irracional muestra que este espacio topológico puede ser inaccesible a las técnicas de la teoría clásica de la medida. Sin embargo, existe un álgebra de von Neumann no conmutativa asociada al espacio de hojas de una foliación y, una vez más, esto le da a un espacio que de otro modo sería ininteligible una buena estructura geométrica.
La geometría algebraica estudia las propiedades geométricas de las ecuaciones polinómicas . Los polinomios son un tipo de función que se define a partir de las operaciones aritméticas básicas de suma y multiplicación. Por ello, están estrechamente vinculados al álgebra. La geometría algebraica ofrece una forma de aplicar técnicas geométricas a cuestiones de álgebra pura, y viceversa.
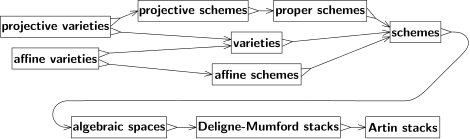
Antes de la década de 1940, la geometría algebraica trabajaba exclusivamente sobre los números complejos, y la variedad más fundamental era el espacio proyectivo. La geometría del espacio proyectivo está estrechamente relacionada con la teoría de la perspectiva , y su álgebra se describe mediante polinomios homogéneos . Todas las demás variedades se definían como subconjuntos del espacio proyectivo. Las variedades proyectivas eran subconjuntos definidos por un conjunto de polinomios homogéneos. En cada punto de la variedad proyectiva, todos los polinomios del conjunto debían ser iguales a cero. El complemento del conjunto cero de un polinomio lineal es un espacio afín, y una variedad afín era la intersección de una variedad proyectiva con un espacio afín.
André Weil se dio cuenta de que el razonamiento geométrico podía aplicarse en ocasiones en situaciones de teoría de números en las que los espacios en cuestión podían ser discretos o incluso finitos. En pos de esta idea, Weil reescribió los fundamentos de la geometría algebraica, liberando a la geometría algebraica de su dependencia de los números complejos e introduciendo variedades algebraicas abstractas que no estaban insertas en el espacio proyectivo. Estas ahora se denominan simplemente variedades .
El tipo de espacio que subyace a la mayor parte de la geometría algebraica moderna es incluso más general que las variedades algebraicas abstractas de Weil. Fue introducido por Alexander Grothendieck y se denomina esquema . Una de las motivaciones de la teoría de esquemas es que los polinomios están inusualmente estructurados entre funciones y, en consecuencia, las variedades algebraicas son rígidas. Esto presenta problemas cuando se intenta estudiar situaciones degeneradas. Por ejemplo, casi cualquier par de puntos en un círculo determina una línea única llamada línea secante y, a medida que los dos puntos se mueven alrededor del círculo, la línea secante varía continuamente. Sin embargo, cuando los dos puntos chocan, la línea secante degenera en una línea tangente. La línea tangente es única, pero la geometría de esta configuración (un solo punto en un círculo) no es lo suficientemente expresiva como para determinar una línea única. Estudiar situaciones como esta requiere una teoría capaz de asignar datos adicionales a las situaciones degeneradas.
Uno de los componentes básicos de un esquema es un espacio topológico. Los espacios topológicos tienen funciones continuas, pero las funciones continuas son demasiado generales para reflejar la estructura algebraica subyacente de interés. Por lo tanto, el otro ingrediente de un esquema es un haz en el espacio topológico, llamado "haz de estructura". En cada subconjunto abierto del espacio topológico, el haz especifica una colección de funciones, llamadas "funciones regulares". El espacio topológico y el haz de estructura juntos son necesarios para satisfacer las condiciones que significan que las funciones provienen de operaciones algebraicas.
Al igual que las variedades, los esquemas se definen como espacios que se modelan localmente en un espacio familiar. En el caso de las variedades, el espacio familiar es el espacio euclidiano. Para un esquema, los modelos locales se denominan esquemas afines . Los esquemas afines proporcionan un vínculo directo entre la geometría algebraica y el álgebra conmutativa . Los objetos fundamentales de estudio en el álgebra conmutativa son los anillos conmutativos . Si es un anillo conmutativo, entonces existe un esquema afín correspondiente que traduce la estructura algebraica de en geometría. A la inversa, cada esquema afín determina un anillo conmutativo, es decir, el anillo de secciones globales de su haz de estructura. Estas dos operaciones son mutuamente inversas, por lo que los esquemas afines proporcionan un nuevo lenguaje con el que estudiar cuestiones de álgebra conmutativa. Por definición, cada punto de un esquema tiene un vecindario abierto que es un esquema afín.
Existen muchos esquemas que no son afines. En particular, los espacios proyectivos satisfacen una condición llamada propiedad, que es análoga a la compacidad. Los esquemas afines no pueden ser propios (excepto en situaciones triviales, como cuando el esquema tiene un solo punto), y por lo tanto ningún espacio proyectivo es un esquema afín (excepto los espacios proyectivos de dimensión cero). Los esquemas proyectivos, es decir, aquellos que surgen como subesquemas cerrados de un espacio proyectivo, son la familia de esquemas más importante. [12]
Se han introducido varias generalizaciones de esquemas. Michael Artin definió un espacio algebraico como el cociente de un esquema por las relaciones de equivalencia que definen los morfismos de étale . Los espacios algebraicos conservan muchas de las propiedades útiles de los esquemas y, al mismo tiempo, son más flexibles. Por ejemplo, el teorema de Keel-Mori se puede utilizar para demostrar que muchos espacios de módulos son espacios algebraicos.
Más general que un espacio algebraico es una pila de Deligne-Mumford . Las pilas DM son similares a los esquemas, pero permiten singularidades que no se pueden describir únicamente en términos de polinomios. Desempeñan el mismo papel para los esquemas que los orbifolds para las variedades . Por ejemplo, el cociente del plano afín por un grupo finito de rotaciones alrededor del origen produce una pila de Deligne-Mumford que no es un esquema ni un espacio algebraico. Lejos del origen, el cociente por la acción de grupo identifica conjuntos finitos de puntos igualmente espaciados en un círculo. Pero en el origen, el círculo consta de un solo punto, el origen mismo, y la acción de grupo fija este punto. En la pila DM de cociente, sin embargo, este punto viene con el dato adicional de ser un cociente. Este tipo de estructura refinada es útil en la teoría de espacios de módulos y, de hecho, se introdujo originalmente para describir módulos de curvas algebraicas .
Otra generalización son las pilas algebraicas , también llamadas pilas de Artin. Las pilas de DM están limitadas a cocientes por acciones de grupos finitos. Si bien esto es suficiente para muchos problemas en la teoría de módulos, es demasiado restrictivo para otros, y las pilas de Artin permiten cocientes más generales.

En su trabajo sobre las conjeturas de Weil , Grothendieck introdujo un nuevo tipo de topología, ahora llamada topología de Grothendieck . Un espacio topológico (en el sentido ordinario) axiomatiza la noción de "proximidad", haciendo que dos puntos estén cerca si y solo si se encuentran en muchos de los mismos conjuntos abiertos. Por el contrario, una topología de Grothendieck axiomatiza la noción de "cobertura". Una cobertura de un espacio es una colección de subespacios que contienen en conjunto toda la información del espacio circundante. Dado que los haces se definen en términos de coberturas, una topología de Grothendieck también puede verse como una axiomatización de la teoría de haces.
El trabajo de Grothendieck sobre sus topologías lo llevó a la teoría de los topos . En sus memorias Récoltes et Semailles , los llamó su "concepción más vasta". [13] Un haz (ya sea en un espacio topológico o con respecto a una topología de Grothendieck) se utiliza para expresar datos locales. La categoría de todos los haces conlleva todas las formas posibles de expresar datos locales. Dado que los espacios topológicos se construyen a partir de puntos, que son en sí mismos un tipo de datos locales, la categoría de haces puede usarse como reemplazo del espacio original. En consecuencia, Grothendieck definió un topos como una categoría de haces y estudió los topos como objetos de interés por derecho propio. Estos ahora se denominan topos de Grothendieck .
Todo espacio topológico determina un topos, y viceversa. Hay espacios topológicos en los que al tomar el topos asociado se pierde información, pero estos generalmente se consideran patológicos. (Una condición necesaria y suficiente es que el espacio topológico sea un espacio sobrio ). Por el contrario, hay topos cuyos espacios topológicos asociados no capturan el topos original. Pero, lejos de ser patológicos, estos topos pueden ser de gran interés matemático. Por ejemplo, la teoría de la cohomología étale de Grothendieck (que eventualmente condujo a la prueba de las conjeturas de Weil) puede formularse como cohomología en el topos étale de un esquema, y este topos no proviene de un espacio topológico.
Los espacios topológicos, de hecho, conducen a topos muy especiales llamados locales . El conjunto de subconjuntos abiertos de un espacio topológico determina una red . Los axiomas para un espacio topológico hacen que estas redes sean álgebras de Heyting completas . La teoría de locales toma esto como su punto de partida. Un local se define como un álgebra de Heyting completa, y las propiedades elementales de los espacios topológicos se vuelven a expresar y refutar en estos términos. El concepto de local resulta ser más general que el de espacio topológico, en el sentido de que cada espacio topológico sobrio determina una única local, pero muchos locales interesantes no provienen de espacios topológicos. Debido a que los locales no necesitan tener puntos, el estudio de los locales se llama, en tono de broma, topología sin sentido .
Los topos también muestran profundas conexiones con la lógica matemática. Cada topo de Grothendieck tiene un haz especial llamado clasificador de subobjetos. Este clasificador de subobjetos funciona como el conjunto de todos los valores de verdad posibles. En el topo de conjuntos, el clasificador de subobjetos es el conjunto , que corresponde a "Falso" y "Verdadero". Pero en otros topos, el clasificador de subobjetos puede ser mucho más complicado. Lawvere y Tierney reconocieron que la axiomatización del clasificador de subobjetos producía un tipo de topo más general, ahora conocido como topo elemental , y que los topos elementales eran modelos de lógica intuicionista . Además de proporcionar una forma poderosa de aplicar herramientas de la lógica a la geometría, esto hizo posible el uso de métodos geométricos en lógica.
Según Kevin Arlin,
Sin embargo, Bourbaki propuso una definición general de “estructura” [2] que abarca todos los tipos de espacios mencionados anteriormente, (¿casi?) todos los tipos de estructuras matemáticas utilizadas hasta ahora, y más. Proporciona una definición general de isomorfismo y justifica la transferencia de propiedades entre estructuras isomorfas. Sin embargo, nunca se utilizó activamente en la práctica matemática (ni siquiera en los tratados matemáticos escritos por el propio Bourbaki). He aquí las últimas frases de una reseña de Robert Reed [14] de un libro de Leo Corry:
Para obtener más información sobre estructuras matemáticas, consulte Wikipedia: estructura matemática , definiciones equivalentes de estructuras matemáticas y transporte de estructura .
La distinción entre "espacios" geométricos y "estructuras" algebraicas es a veces clara, a veces elusiva. Claramente, los grupos son algebraicos, mientras que los espacios euclidianos son geométricos. Los módulos sobre anillos son tan algebraicos como los grupos. En particular, cuando el anillo parece ser un cuerpo , el módulo parece ser un espacio lineal ; ¿es algebraico o geométrico? En particular, cuando es de dimensión finita, sobre números reales, y dotado de producto interno , se convierte en espacio euclidiano ; ahora geométrico. El cuerpo (¿algebraico?) de números reales es el mismo que la línea real (¿geométrica?) . Su cierre algebraico , el cuerpo (¿algebraico?) de números complejos , es el mismo que el plano complejo (¿geométrico?) . Es, en primer lugar, "un lugar en el que hacemos análisis " (en lugar de álgebra o geometría).
Todo espacio tratado en la sección "Tipos de espacios" anterior, excepto las subsecciones "Geometría no conmutativa", "Esquemas" y "Topoi", es un conjunto (el "conjunto base principal" de la estructura, según Bourbaki) dotado de alguna estructura adicional; los elementos del conjunto base se denominan habitualmente "puntos" de este espacio. Por el contrario, los elementos de (el conjunto base de) una estructura algebraica no suelen denominarse "puntos".
Sin embargo, a veces se utiliza más de un conjunto base principal. Por ejemplo, la geometría proyectiva bidimensional puede formalizarse mediante dos conjuntos base , el conjunto de puntos y el conjunto de líneas. Además, una característica sorprendente de los planos proyectivos es la simetría de los papeles que desempeñan los puntos y las líneas . Un ejemplo menos geométrico: un grafo puede formalizarse mediante dos conjuntos base , el conjunto de vértices (también llamados nodos o puntos) y el conjunto de aristas (también llamados arcos o líneas). En general, Bourbaki estipula un número finito de conjuntos base principales y un número finito de conjuntos base auxiliares .
Muchas estructuras matemáticas de carácter geométrico tratadas en las subsecciones "Geometría no conmutativa", "Esquemas" y "Topos" anteriores no estipulan un conjunto base de puntos. Por ejemplo, la " topología sin puntos " (en otras palabras, topología sin puntos o teoría de localidades) comienza con un único conjunto base cuyos elementos imitan conjuntos abiertos en un espacio topológico (pero no son conjuntos de puntos); véase también mereotopología y geometría sin puntos .
![]() Este artículo fue enviado a WikiJournal of Science para su revisión académica externa por pares en 2017 (informes de los revisores). El contenido actualizado fue reintegrado a la página de Wikipedia bajo una licencia CC-BY-SA-3.0 ( 2018 ). La versión de registro revisada es: Boris Tsirelson ; et al. (1 de junio de 2018). "Espacios en matemáticas" (PDF) . WikiJournal of Science . 1 (1): 2. doi : 10.15347/WJS/2018.002 . ISSN 2470-6345. Wikidata Q55120290.
Este artículo fue enviado a WikiJournal of Science para su revisión académica externa por pares en 2017 (informes de los revisores). El contenido actualizado fue reintegrado a la página de Wikipedia bajo una licencia CC-BY-SA-3.0 ( 2018 ). La versión de registro revisada es: Boris Tsirelson ; et al. (1 de junio de 2018). "Espacios en matemáticas" (PDF) . WikiJournal of Science . 1 (1): 2. doi : 10.15347/WJS/2018.002 . ISSN 2470-6345. Wikidata Q55120290.