
Una constante matemática es un número cuyo valor está fijado por una definición inequívoca, a menudo referida mediante un símbolo especial (por ejemplo, una letra del alfabeto ) o mediante nombres matemáticos para facilitar su uso en múltiples problemas matemáticos . [1] Las constantes surgen en muchas áreas de las matemáticas , y constantes como e y π aparecen en contextos tan diversos como la geometría , la teoría de números , la estadística y el cálculo .
Algunas constantes surgen de manera natural por un principio fundamental o una propiedad intrínseca, como la relación entre la circunferencia y el diámetro de un círculo ( π ). Otras constantes son notables más por razones históricas que por sus propiedades matemáticas. Las constantes más populares se han estudiado a lo largo de los siglos y se han calculado hasta muchos decimales.
Todas las constantes matemáticas nombradas son números definibles y, por lo general, también son números computables ( la constante de Chaitin es una excepción significativa).
Estas son constantes que uno probablemente encontrará durante la educación preuniversitaria en muchos países.

La raíz cuadrada de 2 , a menudo conocida como raíz de 2 o constante de Pitágoras , y escrita como √ 2 , es el único número real positivo que, al multiplicarse por sí mismo, da el número 2. Se le llama con más precisión raíz cuadrada principal de 2 , para distinguirla del número negativo con la misma propiedad.
Geométricamente, la raíz cuadrada de 2 es la longitud de la diagonal de un cuadrado cuyos lados miden una unidad de longitud ; esto se desprende del teorema de Pitágoras . Es un número irracional , posiblemente el primer número conocido como tal, y un número algebraico . Su valor numérico truncado a 50 decimales es:
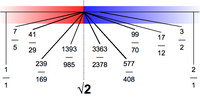
Alternativamente, la aproximación rápida 99/70 (≈ 1,41429) para la raíz cuadrada de dos se utilizaba con frecuencia antes del uso común de calculadoras electrónicas y computadoras . A pesar de tener un denominador de solo 70, difiere del valor correcto en menos de 1/10 000 (aproximadamente 7,2 × 10 −5 ).
Su fracción continua simple es periódica y está dada por:
La constante π (pi) tiene una definición natural en la geometría euclidiana como la relación entre la circunferencia y el diámetro de un círculo. Se puede encontrar en muchos otros lugares de las matemáticas: por ejemplo, la integral de Gauss , las raíces complejas de la unidad y las distribuciones de Cauchy en probabilidad . Sin embargo, su ubicuidad no se limita a las matemáticas puras. Aparece en muchas fórmulas de la física, y varias constantes físicas se definen de forma más natural con π o su recíproco factorizado. Por ejemplo, la función de onda del estado fundamental del átomo de hidrógeno es
¿Dónde está el radio de Bohr ?
π es un número irracional , un número trascendental y un período algebraico .
El valor numérico de π es aproximadamente:
Las fracciones 22/7 y 355/113 dan aproximaciones inusualmente buenas .
Memorizar y calcular cada vez más dígitos de π es una tarea que supone un récord mundial.
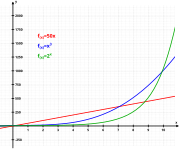
El número de Euler e , también conocido como constante de crecimiento exponencial , aparece en muchas áreas de las matemáticas, y una posible definición del mismo es el valor de la siguiente expresión:
La constante e está intrínsecamente relacionada con la función exponencial .
El matemático suizo Jacob Bernoulli descubrió que e surge en el interés compuesto : si una cuenta comienza en $1 y produce intereses a una tasa anual R , entonces, como el número de períodos de capitalización por año tiende a infinito (una situación conocida como capitalización continua ), la cantidad de dinero al final del año se acercará a e R dólares.
La constante e también tiene aplicaciones en la teoría de la probabilidad , donde surge de una manera que no está obviamente relacionada con el crecimiento exponencial. Como ejemplo, supongamos que se juega n veces a una máquina tragamonedas con una probabilidad de ganar de uno en n ; entonces, para un valor n grande (por ejemplo, un millón), la probabilidad de que no se gane nada tenderá a 1/ e a medida que n tiende a infinito.
Otra aplicación de e , descubierta en parte por Jacob Bernoulli junto con el matemático francés Pierre Raymond de Montmort , se encuentra en el problema de los trastornos , también conocido como el problema del guardarropa . [2] Aquí, n invitados son invitados a una fiesta, y en la puerta cada invitado guarda su sombrero con el mayordomo, quien luego los coloca en cajas etiquetadas. El mayordomo no sabe el nombre de los invitados y, por lo tanto, debe colocarlos en cajas seleccionadas al azar. El problema de de Montmort es: ¿cuál es la probabilidad de que ninguno de los sombreros se coloque en la caja correcta? La respuesta es
que, a medida que n tiende a infinito, se acerca a 1/ e .
e es un número irracional y un número trascendental.
El valor numérico de e es aproximadamente:

La unidad imaginaria o número imaginario unitario , denotada como i , es un concepto matemático que extiende el sistema de números reales al sistema de números complejos . La propiedad principal de la unidad imaginaria es que i 2 = −1 . El término " imaginario " fue acuñado porque no existe ningún número ( real ) que tenga un cuadrado negativo .
De hecho, hay dos raíces cuadradas complejas de −1, a saber, i y − i , así como hay dos raíces cuadradas complejas de cualquier otro número real (excepto cero , que tiene una raíz cuadrada doble).
En contextos en los que el símbolo i es ambiguo o problemático, a veces se utiliza j o la iota griega ( ι ). Este es el caso en particular de la ingeniería eléctrica y la ingeniería de sistemas de control , donde la unidad imaginaria se suele denotar con j , porque i se utiliza comúnmente para denotar la corriente eléctrica .
Estas son constantes que se encuentran con frecuencia en las matemáticas superiores .

El número φ , también llamado proporción áurea , aparece con frecuencia en geometría , particularmente en figuras con simetría pentagonal . De hecho, la longitud de la diagonal de un pentágono regular es φ por su lado. Los vértices de un icosaedro regular son los de tres rectángulos áureos mutuamente ortogonales . También aparece en la sucesión de Fibonacci , relacionada con el crecimiento por recursión . [3] Kepler demostró que es el límite de la proporción de números de Fibonacci consecutivos. [4] La proporción áurea tiene la convergencia más lenta de cualquier número irracional. [5] Es, por esa razón, uno de los peores casos del teorema de aproximación de Lagrange y es un caso extremo de la desigualdad de Hurwitz para aproximaciones diofánticas . Esta puede ser la razón por la que los ángulos cercanos a la proporción áurea a menudo aparecen en la filotaxis (el crecimiento de las plantas). [6] Es aproximadamente igual a:
o, más precisamente

La constante de Euler o constante de Euler-Mascheroni se define como la diferencia límite entre la serie armónica y el logaritmo natural :
Aparece con frecuencia en matemáticas, especialmente en contextos de teoría de números como el tercer teorema de Mertens o la tasa de crecimiento de la función divisor . Tiene relaciones con la función gamma y sus derivadas , así como con la función zeta y existen muchas integrales y series diferentes que involucran .
A pesar de la ubicuidad de la constante de Euler-Mascheroni, muchas de sus propiedades siguen siendo desconocidas. Entre ellas, las grandes preguntas abiertas sobre si es un número racional o irracional y si es algebraico o trascendental. De hecho, se la ha descrito como una constante matemática "sólo a la sombra y en importancia". [7]
El valor numérico de es aproximadamente:
La constante de Apery se define como la suma de los recíprocos de los cubos de los números naturales: Es el valor especial de la función zeta de Riemann en . La búsqueda para encontrar un valor exacto para esta constante en términos de otras constantes conocidas y funciones elementales se originó cuando Euler resolvió el famoso problema de Basilea al obtener . Hasta la fecha, no se ha encontrado tal valor y se conjetura que no existe ninguno. [8] Sin embargo, existen muchas representaciones de en términos de series infinitas.
La constante de Apéry surge naturalmente en una serie de problemas físicos, incluidos los términos de segundo y tercer orden de la relación giromagnética del electrón , calculada utilizando electrodinámica cuántica . [9]
Se sabe que es un número irracional que fue demostrado por el matemático francés Roger Apéry en 1979. Sin embargo, no se sabe si es algebraico o trascendental.
El valor numérico de la constante de Apéry es aproximadamente:
La constante de Catalan se define por la suma alternada de los cuadrados de los números impares:
Es el valor especial de la función beta de Dirichlet en . La constante de Catalan aparece con frecuencia en combinatoria y teoría de números y también fuera de las matemáticas, como en el cálculo de la distribución de masa de las galaxias espirales . [10]
Las preguntas sobre la naturaleza aritmética de esta constante también permanecen sin respuesta, habiéndosela llamado "posiblemente la constante más básica cuya irracionalidad y trascendencia (aunque fuertemente sospechadas) siguen sin demostrarse". [11] Existen muchas representaciones integrales y en serie de la constante de Catalan.
Debe su nombre al matemático francés y belga Charles Eugène Catalan .
El valor numérico de es aproximadamente:
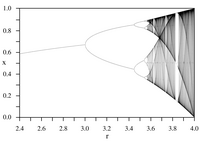
Las iteraciones de mapas continuos sirven como los ejemplos más simples de modelos para sistemas dinámicos . [12] Nombradas en honor al físico matemático Mitchell Feigenbaum , las dos constantes de Feigenbaum aparecen en tales procesos iterativos: son invariantes matemáticos de mapas logísticos con puntos máximos cuadráticos [7] y sus diagramas de bifurcación . Específicamente, la constante α es la relación entre el ancho de una púa y el ancho de una de sus dos subpúas, y la constante δ es la relación límite de cada intervalo de bifurcación con el siguiente entre cada bifurcación de duplicación de período .
El mapa logístico es una aplicación polinómica , citada a menudo como un ejemplo arquetípico de cómo el comportamiento caótico puede surgir de ecuaciones dinámicas no lineales muy simples . El mapa se popularizó en un artículo seminal de 1976 del biólogo australiano Robert May [13] , en parte como un modelo demográfico de tiempo discreto análogo a la ecuación logística creada por primera vez por Pierre François Verhulst . La ecuación diferencial pretende capturar los dos efectos de la reproducción y la inanición.
Las constantes de Feigenbaum en la teoría de bifurcaciones son análogas a π en geometría y a e en cálculo . No se sabe si alguna de ellas es irracional o incluso trascendental. Sin embargo, existen pruebas de su universalidad . [14]
Los respectivos valores numéricos aproximados de δ y α son:
Algunas constantes, como la raíz cuadrada de 2 , la constante de Liouville y la constante de Champernowne :

no son invariantes matemáticos importantes pero conservan interés al ser simples representantes de conjuntos especiales de números, los números irracionales , [16] los números trascendentales [17] y los números normales (en base 10) [18] respectivamente. El descubrimiento de los números irracionales se suele atribuir al pitagórico Hipaso de Metaponto , quien demostró, muy probablemente geométricamente, la irracionalidad de la raíz cuadrada de 2. En cuanto a la constante de Liouville, llamada así por el matemático francés Joseph Liouville , fue el primer número que se demostró trascendental. [19]
En el subcampo de la informática de la teoría de la información algorítmica , la constante de Chaitin es el número real que representa la probabilidad de que una máquina de Turing elegida al azar se detenga, formada a partir de una construcción debida al matemático y científico informático argentino - estadounidense Gregory Chaitin . La constante de Chaitin, aunque no es computable , se ha demostrado que es trascendental y normal . La constante de Chaitin no es universal, depende en gran medida de la codificación numérica utilizada para las máquinas de Turing; sin embargo, sus propiedades interesantes son independientes de la codificación.
Es habitual expresar el valor numérico de una constante dando su representación decimal (o solo los primeros dígitos de la misma). Por dos razones, esta representación puede causar problemas. En primer lugar, aunque todos los números racionales tienen una expansión decimal finita o que se repite constantemente, los números irracionales no tienen dicha expresión, lo que hace que sea imposible describirlos completamente de esta manera. Además, la expansión decimal de un número no es necesariamente única. Por ejemplo, las dos representaciones 0,999... y 1 son equivalentes [20] [21] en el sentido de que representan el mismo número.
Calcular los dígitos de la expansión decimal de las constantes ha sido una tarea común durante muchos siglos. Por ejemplo, el matemático alemán Ludolph van Ceulen del siglo XVI pasó gran parte de su vida calculando los primeros 35 dígitos de pi. [22] Utilizando computadoras y supercomputadoras , algunas de las constantes matemáticas, incluidas π, e y la raíz cuadrada de 2, se han calculado hasta alcanzar más de cien mil millones de dígitos. Se han desarrollado algoritmos rápidos , algunos de los cuales, como la constante de Apéry , son inesperadamente rápidos.
Algunas constantes difieren tanto de las habituales que se ha inventado una nueva notación para representarlas de forma razonable. El número de Graham ilustra esto, ya que se utiliza la notación de flecha hacia arriba de Knuth . [23] [24]
Puede resultar interesante representarlas mediante fracciones continuas para realizar diversos estudios, incluido el análisis estadístico. Muchas constantes matemáticas tienen una forma analítica , es decir, se pueden construir utilizando operaciones bien conocidas que se prestan fácilmente al cálculo. Sin embargo, no todas las constantes tienen formas analíticas conocidas; la constante de Grossman [25] y la constante de Foias [26] son ejemplos.
La simbolización de constantes con letras es un método frecuente para hacer que la notación sea más concisa. Una convención común , iniciada por René Descartes en el siglo XVII y Leonhard Euler en el siglo XVIII, es utilizar letras minúsculas del comienzo del alfabeto latino o del alfabeto griego cuando se trabaja con constantes en general.
Sin embargo, para constantes más importantes, los símbolos pueden ser más complejos y tener una letra extra, un asterisco , un número, una lemniscata o utilizar alfabetos diferentes como el hebreo , el cirílico o el gótico . [24]
A veces, el símbolo que representa una constante es una palabra entera. Por ejemplo, el sobrino de 9 años del matemático estadounidense Edward Kasner acuñó los nombres de googol y googolplex . [24] [27]
Otros nombres están relacionados con el significado de la constante ( constante parabólica universal , constante de primos gemelos , ...) o con una persona específica ( constante de Sierpiński , constante de Josephson , etc.).
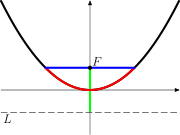
*Se desconoce el valor de la constante de Mill, pero se ha calculado que es aproximadamente 1,3063778838... si la hipótesis de Riemann es cierta.
Abreviaturas utilizadas: