Paralaje
Muchos animales, junto con los humanos, tienen dos ojos con campos visuales superpuestos que utilizan el paralaje para obtener percepción de profundidad; este proceso se conoce como estereopsis.
En visión por ordenador el efecto se utiliza para la visión estereoscópica por ordenador, y existe un dispositivo llamado telémetro de paralaje que lo utiliza para encontrar la distancia, y en algunas variaciones también la altitud a un objetivo.
Esta es la base de la estereopsis, el proceso por el cual el cerebro explota el paralaje debido a las diferentes vistas del ojo para obtener la percepción de la profundidad y estimar las distancias a los objetos.
Al observar el paralaje, medir ángulos, y utilizando la geometría, se puede determinar la distancia.
En la paralaje, el triángulo es extremadamente largo y estrecho, y midiendo tanto su lado más corto (el movimiento del observador) como el pequeño ángulo superior (siempre inferior a 1 arcosegundo,[5] dejando los otros dos cerca de 90 grados), se puede determinar la longitud de los lados largos (en la práctica considerados iguales).
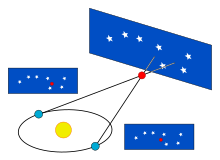
Cuando la Tierra orbita alrededor del Sol, la posición de las estrellas cercanas parece desplazarse ligeramente respecto al fondo más lejano.
[8][9] La misión espacial Gaia proporcionó distancias igualmente precisas a la mayoría de las estrellas más brillantes que la 15.ª magnitud.
En el año 1838, Friedrich Bessel fue el primero en determinar el paralaje de una estrella, 61 Cygni, en la constelación del Cisne.
A mayor distancia el paralaje es menor, y los errores cometidos se van haciendo más y más significativos, de modo que a partir de los 100 años luz ya no es fiable el paralaje anual trigonométrico para determinar distancias estelares.
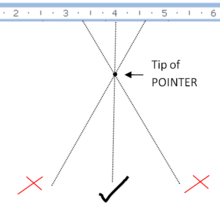
Un error similar ocurre cuando se lee la posición de un puntero contra una escala en un instrumento como un multímetro analógico.
Para ayudar al usuario a evitar este problema, la escala se imprime a veces sobre una estrecha franja de espejo, y el ojo del usuario se coloca de modo que el puntero oculte su reflejo, garantizando que la línea de visión del usuario sea perpendicular al espejo y, por tanto, a la escala.
El mismo efecto altera la velocidad leída en el velocímetro de un coche por un conductor situado delante y un pasajero situado a un lado, los valores leídos en un gratícula, no en contacto real con la pantalla de un osciloscopio, etc.
Es decir, el visor no previsualiza la propia imagen que le ofrece el objetivo.
En una cámara réflex de un solo objetivo no hay error de paralaje, ya que el fotógrafo observa la imagen a través del objetivo, reflejada por el espejo hacia el pentaprisma y el visor.
Este tipo de error también afecta al ojo humano; si no está a la altura del objeto observado, se pueden percibir falsas imágenes.
En los laboratorios, hay que tener en cuenta este error, pues al llenar probetas u otros envases aforados, si no se observan desde la altura correcta, se aprecian mal las cantidades de materia, con los consecuentes errores en los cálculos.
Para la correcta lectura la aguja debía ocultar su propio reflejo (la observación se efectuaba cerrando un ojo).
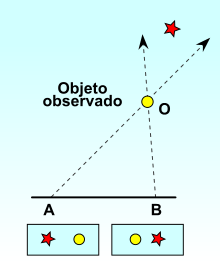
Al proyectar el objeto observado O contra un fondo suficientemente distante, la posición de O varía según el punto de vista en A o en B. Desde A, el objeto observado parece estar a la derecha de la lejana estrella roja, mientras que desde B se ve a la izquierda de aquella.
El ángulo AOB se denomina ángulo de paralaje , que abarca el segmento AB desde O.