Péndulo

El péndulo (del latín pendŭlus, pendiente)[1]​ es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla, u otro dispositivo que pueda mantener fijo el sistema.

[3]​ Muchas fuentes[4]​[5]​[6]​[7]​ afirman que el astrónomo egipcio del siglo X Ibn Yunus utilizaba un péndulo para medir el tiempo, pero se trata de un error originado en 1684 por el historiador británico Edward Bernard.

[8]​[9]​[10]​[11]​ Durante el Renacimiento, se utilizaban grandes péndulos bombeados a mano como fuentes de energía para máquinas manuales de movimiento alternativo, como sierras, fuelles y bombas.

[12]​ Leonardo da Vinci hizo muchos dibujos del movimiento de los péndulos, aunque sin darse cuenta de su valor para la medición del tiempo.

[14]​ Su biógrafo y estudiante, Vincenzo Viviani, indica que su interés se había despertado hacia 1582 por el movimiento oscilatorio de un candelabro suspendido en la catedral de Pisa.

[15]​[16]​ Galileo descubrió que la propiedad importante que hace al péndulo una herramienta útil para medir el tiempo, denominada isocronismo; el período del péndulo es aproximadamente independiente de la amplitud o el desplazamiento del balanceo.

En 1656 el científico neerlandés Christiaan Huygens construyó el primer reloj de péndulo.

[19]​ Esto supuso una gran mejora respecto a los relojes mecánicos existentes; su mayor precisión pasó de unos 15 minutos de desviación al día a unos 15 segundos al día.

[20]​ Los péndulos se extendieron por Europa a medida que los relojes existentes eran adaptados con ellos.

[21]​ El científico inglés Robert Hooke estudió el péndulo cónico hacia 1666, consistente en un péndulo que se balancea libremente en dos dimensiones, con la bobina girando en un círculo o elipse.

[23]​ Hooke sugirió a Isaac Newton en 1679 que los componentes del movimiento orbital consistían en un movimiento inercial a lo largo de una dirección tangente más un movimiento atractivo en la dirección radial, lo que pudo jugar un papel en la formulación de Newton de la ley de la gravitación universal.

[22]​ Durante su expedición a Cayena, Guayana Francesa en 1671, Jean Richer descubrió que un reloj de péndulo era 2 1⁄2 minutos por día más lento en Cayena que en París.

[26]​[27]​ También llamado péndulo ideal, está constituido por un hilo inextensible de masa despreciable, sostenido por su extremo superior de un punto fijo, con una masa puntual sujeta en su extremo inferior que oscila libremente en un plano vertical fijo.

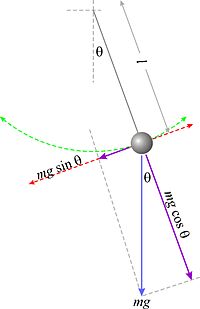
La flecha azul representa el peso de la masa pendular.

Las flechas en color violeta representan las componentes del peso en las direcciones tangencial y normal a la trayectoria.

Aplicando la Segunda ley de Newton en la dirección del movimiento, tenemos

tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura).

El astrónomo y físico italiano Galileo Galilei observó que el periodo de oscilación es independiente de la amplitud, al menos para pequeñas oscilaciones.

Para oscilaciones mayores la relación exacta para el período no es constante con la amplitud e involucra integrales elípticas de primera especie: Donde φ0 es la amplitud angular máxima.

La ecuación anterior puede desarrollarse en serie de Taylor obteniéndose una expresión más útil: Para amplitudes pequeñas, la oscilación puede aproximarse como combinación lineal de funciones trigonométricas.

Para amplitudes grandes puede probarse el ángulo puede expresarse como combinación lineal de funciones elípticas de Jacobi.

Donde, en la última expresión se ha usado la fórmula del ángulo doble y donde además: Realizando en variable

, la solución de las ecuaciones del movimiento puede expresarse como:

es el ángulo que forma la cuerda del péndulo a lo largo de sus oscilaciones (es la variable), y

Es decir, la masa no influye en el movimiento de un péndulo.

Existen dos integrales de movimiento, la energía E y la componente del momento angular paralela al eje vertical Mz.

es el ángulo que forma el hilo o barra del péndulo con la vertical.

La segunda ecuación expresa la constancia de la componente Z del momento angular y por tanto lleva a la relación entre la velocidad de giro polar y el momento angular y por tanto a reescribir la lagrangiana como:

Sin embargo, el movimiento resulta cuasiperiódico, lo cual significa que fijado una posición y una velocidad previas del movimiento existe un tiempo T tal que el movimiento pasará a una distancia tan pequeña como se desee de esa posición con una velocidad tan parecida como se quiera, pero sin repetirse exactamente.

Dada que la región de movimiento además resulta compacta, el conjunto de puntos la trayectoria de un péndulo esférico constituye un conjunto denso sobre una área esférica comprendida entre dos casquetes esféricos.