Oscilador armónico
Se dice que un sistema cualquiera, mecánico, eléctrico, neumático, etc., es un oscilador armónico si, cuando se deja en libertad fuera de su posición de equilibrio, vuelve hacia ella describiendo oscilaciones sinusoidales, o sinusoidales amortiguadas en torno a dicha posición estable.
A medida que la masa se acerca a la posición de equilibrio y que aumenta su velocidad, la energía potencial elástica del resorte se transforma en energía cinética de la masa.
En la realidad, siempre hay una parte de la energía que se transforma en otra forma, debido a la viscosidad del aire o porque el resorte no es perfectamente elástico.
Se supondrá que la fuerza del resorte es estrictamente proporcional al desequilibrio:
La solución de esta ecuación diferencial ordinaria es inmediata: las únicas funciones reales (no complejas) cuya segunda derivada es la misma función con el signo invertido son seno y coseno.
La solución se escribe: Es fácil comprobar que el valor de
Se tratará únicamente el caso más simple, es decir, cuando la fuerza sea proporcional a la velocidad.
y corresponde a la rápida cancelación del efecto de la velocidad inicial.
es más grande y describe la lenta tendencia hacia la posición de equilibrio.
El amortiguamiento crítico corresponde a la tendencia más rápida hacia la situación de equilibrio cuando no sobrepasa esa posición.
Si se disminuye un poco el amortiguamiento el sistema se acerca más rápidamente a la posición de equilibrio, pero sobrepasando la posición oscila en torno a ese punto (tomando valores positivos y negativos).
Como ejemplos, el Q de un vehículo con los amortiguadores en buen estado es algo mayor que 1.
Alternativamente, podemos aplicarle una fuerza cuya intensidad varíe de manera sinusoidal con el tiempo.
La solución de la parte transitoria es la misma la que ya hemos visto (ecuación homogénea).
Ahora la ecuación a resolver es: Pero por supuesto, como en electricidad, sólo la parte real de
El oscilador armónico no perturbado en una dimensión es un ejemplo de sistema integrable, con comportamiento regular.
Sin embargo, el oscilador armónico perturbado puede presentar un comportamiento caótico[3] caracterizado por un atractor extraño.
[4] El oscilador de van der Pol es un caso especial de oscilador con amortiguamiento no lineal, que responde a la ecuación: Fue descrito por primera vez en 1935 por Balthasar van der Pol[5] y presenta comportamiento caótico.
Considérese el caso de un cuerpo sometido a una fuerza unidimensional:
son lo suficientemente pequeñas, uno se puede quedar con la aproximación lineal y despreciar los términos de orden superior: Llamándole
Aquí radica la importancia del oscilador armónico: supone una primera aproximación para el estudio de un sistema cuando se producen pequeñas oscilaciones en torno a su posición (o estado) de equilibrio.
[6] En la figura de la derecha se ha dibujado un circuito oscilante LC (una bobina y un condensador) ideal, es decir sin pérdidas.
La situación continúa así, con la tensión del condensador que disminuye cada vez más rápidamente (porque la corriente aumenta) y la corriente que aumenta más lentamente (porque la tensión disminuye).
La situación continúa del siguiente modo: el condensador se va cargando cada vez más lentamente (porque la corriente disminuye), mientras que la corriente va disminuyendo cada vez más rápidamente (porque la tensión inversa aumenta).
Así, se llega a la situación en la cual la corriente se anula y la tensión del condensador es máxima y del mismo valor que la tensión inicial, pero con sentido opuesto.
Se tiene, pues, este sistema de ecuaciones diferenciales: Para eliminar
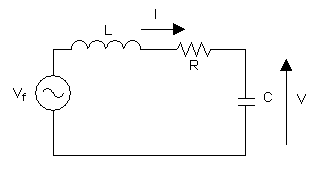
El esquema de la derecha representa un circuito oscilante LC con pérdidas.
El esquema de la derecha muestra un generador conectado a un circuito LC en serie.
, la ecuación es: La expresión se puede reescribir, dándole un aspecto similar a las formas precedentes: Como en el ejemplo mecánico, en régimen estacionario la solución es: donde y
Esta situación es la que se da en el caso clásico, si se define para él una densidad de probabilidad inversamente proporcional a la velocidad de la partícula en cada punto.



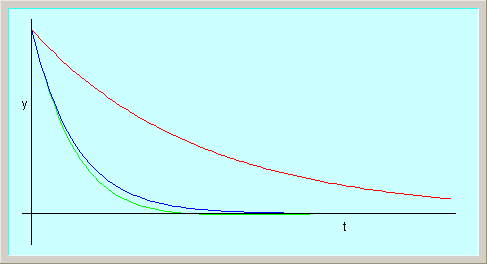
| curva azul: amortiguamiento crítico. |
| curva roja: amortiguamiento doble que el crítico. |
| curva verde: amortiguamiento igual a 90% del amortiguamiento crítico. |