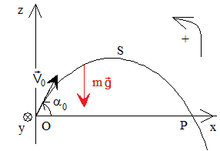
Ecuación de movimiento
Esta ecuación relaciona la derivada temporal de una o varias variables que caracterizan el estado físico del sistema, con otras magnitudes físicas que provocan los cambios en este.
En la dinámica del punto material, la ecuación de movimiento determina la posición futura de un objeto o partícula móvil en función de otras variables como, su velocidad, su aceleración, su masa y cuantas variables le puedan afectar en su movimiento junto con las condiciones iniciales.
Se concibieron dos enfoques básicamente equivalentes conocidos como mecánica lagrangiana y mecánica hamiltoniana, que pueden llegar a un elevado grado de abstracción y formalización en ecuaciones diferenciales.
Los ejemplos clásicos de ecuación del movimiento más conocidos son: {{ap|Mecánica de evolución temporal que involucran ecuaciones diferenciales en derivadas parciales.
Aunque en última instancia, tal como establece la teoría cuántica de campos, las partículas son campos materiales altamente localizados, en teoría de la relatividad se pueden tratar las partículas como entes físicos localizados en el espacio-tiempo.
) la anterior ecuación se reduce a la segunda ley de Newton.
Así la evolución en el tiempo del campo electromagnético, si nos fijamos en un punto concreto del espacio viene medida por las derivadas respecto a la coordenada x
La propia geometría del espacio-tiempo viene representada por un campo tensorial llamado tensor métrico.
El propio campo gravitatorio es una manifestación de que la geometría del espacio-tiempo no es plana o euclídea.
El campo gravitatorio de hecho es proporcional a la curvatura del espacio-tiempo.
A diferencia de las ecuaciones del campo electromagnético, estas ecuaciones del campo gravitatorio o geometría del espacio-tiempo son ecuaciones no lineales debido a la presencia de términos que son el producto de dos Γ.
Los ejemplos más conocidos de ecuación del movimiento son: