Velocidad angular
La magnitud del pseudovector representa la velocidad angular, la tasa a la que el objeto rota o gira, y su dirección es normal respecto al plano de rotación instantáneo o desplazamiento angular.
La unidad SI de velocidad angular es radianes por segundo,[3] siendo el radián una cantidad adimensional, por lo que las unidades SI de velocidad angular pueden enumerarse como s−1.
Por ejemplo, un satélite geoestacionaria completa una órbita por día sobre el ecuador, o 360 grados por 24 horas, y tiene velocidad angular ω = (360°)/(24 h) = 15°/h, o (2π rad)/(24 h) ≈ 0,26 rad/h.
Con un radio orbital de 42.000 km desde el centro de la Tierra, la velocidad del satélite en el espacio es, por tanto, "v" = 42.000 km x 0,26/h ≈ 11.000 km/h.
En un movimiento circular uniforme, dado que una revolución completa representa 2π radianes, tenemos:
Lo que apunta a que puede escribirse en función del producto vectorial r x v Se define el vector velocidad angular ω, como un vector axial paralelo al eje de rotación, cuyo módulo es el valor de la velocidad angular anteriormente definida, o sea (1)
, cuya dirección es la del eje de giro y cuyo sentido coincide con el del avance de un tornillo que girase en el sentido en que lo hace el sólido (regla de la mano derecha).
Llamando et y en a los vectores tangencial y normal, respectivamente, a la trayectoria del punto genérico P, la velocidad de ese punto puede expresarse en la forma (3)
de modo que podemos afirmar: Así pues, conocida la velocidad angular ω queda determinada la distribución de velocidades en todos los puntos del sólido rígido en rotación.
Cualquier vector tridimensional que gira alrededor de un eje con velocidad angular
Y por tanto la velocidad angular se puede definir simplemente como:
Coincide con la definición dada antes para el tensor velocidad angular.
En dicho marco, cada vector puede considerarse como una partícula en movimiento con radio escalar constante.
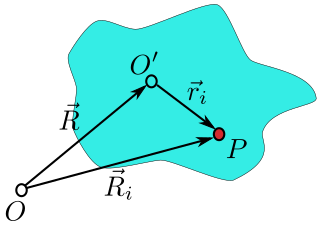
de cualquier punto del cuerpo viene dada por Considere un cuerpo rígido que gira alrededor de un punto fijo O.
es la tasa de cambio temporal del vector marco
Esta fórmula es incompatible con la expresión de la velocidad angular orbital ya que esa fórmula define la velocidad angular para un único punto alrededor de O, mientras que la fórmula de esta sección se aplica a un marco o cuerpo rígido.
tiene que dar cuenta del movimiento de todas las partículas en el cuerpo.
Por lo tanto:[4] Esta base no es ortonormal y es difícil de usar, pero ahora el vector velocidad puede cambiarse al marco fijo o al marco móvil con sólo cambiar las bases.
Este ejemplo se ha realizado utilizando la convención Z-X-Z para los ángulos de Euler.
Las mismas ecuaciones para la velocidad angular pueden obtenerse razonando sobre un cuerpo rígido en rotación.
Aquí no se supone que el cuerpo rígido gire alrededor del origen.
En su lugar, se puede suponer que gira alrededor de un punto arbitrario que se mueve con una velocidad lineal V(t) en cada instante.
Para obtener las ecuaciones, es conveniente imaginar un cuerpo rígido unido a las cuadernas y considerar un sistema de coordenadas fijo respecto al cuerpo rígido.
es la posición de la partícula en algún punto fijo del tiempo, digamos t = 0.
Esta sustitución es útil, porque ahora es sólo la matriz de rotación
, como el cuerpo rígido gira alrededor del punto O.
no giraría si el eje de rotación fuera paralelo a él, y por tanto sólo describiría una rotación sobre un eje perpendicular a él (es decir, no vería la componente del pseudovector velocidad angular paralela a ella, y sólo permitiría calcular la componente perpendicular a ella).
Esta velocidad angular es lo que los físicos llaman velocidad angular de espín del cuerpo rígido, en contraposición a la velocidad angular orbital del punto de referencia O' respecto al origen O.
aunque esa unidad no forma parte del sistema internacional.
Muchos textos emplean aún el "radián por segundo", aunque el radián es una pseudounidad que no forma parte del sistema internacional de unidades y su uso está desrecomendado profesionalmente, aunque se mantiene en algunos contextos con fines didácticos nada más.