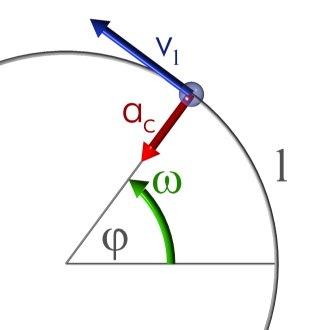
Movimiento circular uniforme
es el que describe un cuerpo que se mueve alrededor de un eje de giro con un radio y una velocidad angular (ω) constantes, trazando una circunferencia y con una aceleración centrípeta.
En este movimiento, la dirección varía en cada instante.
El ángulo abarcado en un movimiento circular es igual al cociente entre la longitud del arco de circunferencia recorrida y el radio.
La longitud del arco y el radio de la circunferencia son magnitudes de longitud, por lo que el desplazamiento angular es una magnitud adimensional, llamada radián.
Partiendo de estos conceptos se estudian las condiciones del movimiento circular uniforme, en cuanto a su trayectoria y espacio recorrido, velocidad y aceleración, según el modelo físico cinemático.
Se considera un sistema de referencia en el plano x,y, con vectores unitarios en la dirección de estos ejes
De modo que el vector de posición de la partícula en función del tiempo es: siendo: Al ser un movimiento uniforme, a iguales incrementos de tiempo le corresponden iguales desplazamientos angulares, lo que se define como velocidad angular (ω):
El ángulo (φ), debe medirse en radianes:
donde s es la longitud del arco de circunferencia Según esta definición: 1 vuelta = 360° = 2π radianes ½ vuelta = 180° = π radianes ¼ de vuelta = 90° = π/2 radianes La velocidad se obtiene a partir del vector de posición mediante derivación tangencial:
El vector velocidad es tangente a la trayectoria y perpendicular al vector posición, lo que puede comprobarse fácilmente efectuando el producto escalar
La aceleración, que para el movimiento circular uniforme es siempre normal, se obtiene a partir del vector velocidad con la derivación:
Así pues, el vector aceleración tiene dirección opuesta al vector de posición, normal a la trayectoria y apuntando siempre hacia el centro de la trayectoria circular, por lo que acostumbramos a referirnos a ella como aceleración normal o centrípeta.
Esta aceleración es la única que experimenta la partícula cuando se mueve con rapidez constante en una trayectoria circular, por lo que la partícula deberá ser atraída hacia el centro mediante una fuerza centrípeta que la aparte de una trayectoria rectilínea, como correspondería por la ley de inercia.
En dos dimensiones la composición de dos movimientos armónicos de la misma frecuencia y amplitud, convenientemente desfasados, dan lugar a un movimiento circular uniforme.
Por ejemplo un movimiento bidimensional dado por las ecuaciones:
De hecho las órbitas planetarias circulares pueden entenderse como la composición de dos movimientos armónicos según dos direcciones mutuamente perpendiculares.
representa el tiempo necesario para que el móvil complete una vuelta y viene dado por:
mide el número de revoluciones o vueltas completadas por el móvil en la unidad de tiempo y viene dada por:
Por consiguiente, la frecuencia es la inversa del período:
Si bien la teoría especial de la relatividad permite que una partícula no cargada esté en movimiento circular uniforme, esto en general no resulta posible para una partícula cargada a la que no se le suministra energía adicional.
Esto se debe a que una partícula cargada acelerada emite radicación electromagnética perdiendo energía en ese proceso.
Además, en la mecánica relativista el cociente entre la fuerza centrípeta y la aceleración centrípeta, es diferente del cociente entre la fuerza tangencial y la aceleración tangencial.
Esto introduce una diferencia fundamental con el caso newtoniano: la aceleración y la fuerza relativistas no son vectores necesariamente paralelos:
De la relación anterior, se deduce que la fuerza y la aceleración solo son paralelas en dos casos:
El primer caso se da cuando la aceleración y la velocidad son perpendiculares, cosa que sucede en el movimiento circular uniforme (o helicoidal uniforme).
El segundo caso se da en un movimiento rectilíneo.
En cualquier otro tipo de movimiento en general la fuerza y la aceleración no serán permanentemente paralelas.
Los estados estacionarios de una partícula en un anillo son el análogo cuántico del movimiento circular uniforme.
Para una partícula moviéndose sobre un anillo con momento angular bien definido la función de onda viene dada por:
Un hecho interesante es que las predicciones para una partícula cargada, en movimiento circular uniforme, es que esta no tiene porqué emitir fotones, de la misma manera que el electrón orbitante alrededor del núcleo atómico no emite energía, por ser el valor resultante de la aceleración vectorial nula, al ser la distribución simétrica respecto al núcleo atómico.