Fuerza centrípeta

Se conoce como fuerza centrípeta a la fuerza o al componente de la fuerza que actúa sobre un objeto en movimiento que pasa por una trayectoria curvilínea y que está dirigida hacia el centro de curvatura de la trayectoria.En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.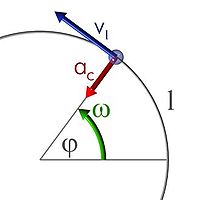La fuerza centrípeta se dirige perpendicularmente al movimiento y también a lo largo del radio hacia el centro de la trayectoria circular.[3]​[4]​ La descripción matemática fue derivada en 1659 por el físico holandés Christiaan Huygens.Por segunda ley de Newton, la causa de la aceleración es una fuerza neta que actúa sobre el objeto y que es proporcional a su masa m y a su aceleración.En el caso de movimiento circular uniforme, las velocidades tienen magnitud constante.Expresado mediante el período orbital T para una revolución del círculo,En los aceleradores de partículas, la velocidad puede ser muy alta (cercana a la velocidad de la luz en el vacío) por lo que la misma masa en reposo ejerce ahora una mayor inercia (masa relativista) requiriendo así una mayor fuerza para la misma aceleración centrípeta, por lo que la ecuación se convierte en:[10]​que es la tasa de cambio del momento relativistaCuando un satélite está en órbita alrededor de un planeta, se considera que la gravedad es una fuerza centrípeta aunque en el caso de las órbitas excéntricas, la fuerza gravitatoria se dirige hacia el foco, y no hacia el centro instantáneo de curvatura.[11]​ Otro ejemplo de fuerza centrípeta surge en la hélice que se traza cuando una partícula cargada se mueve en un campo magnético uniforme en ausencia de otras fuerzas externas.Los objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad.Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración.en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:Supongamos que atamos una pelota con una cuerda y la hacemos girar en círculo a velocidad angular constante.La pelota se mueve en una trayectoria circular porque la cuerda ejerce sobre ella una fuerza centrípeta.Por tanto, esta fuerza siempre va actuar hacia el centro de la trayectoria.El problema reside en que en un sistema de referencia en rotación, la fuerza centrífuga (ficticia) intuida por un observador en reposo en dicho referencial coincide en magnitud –pero en sentido contrario– con la fuerza centrípeta (real) necesaria para mantener un cuerpo en reposo en tal sistema de referencia en rotación.Una excepción ocurre cuando el centro de masas no coincide con el centro geométrico del objeto sobre el cual actúan las fuerzas, con lo que hay que poner especial énfasis sobre la dirección de la fuerza centrípeta y los puntos donde actúa.Un ejemplo claro de este fenómeno ocurre con la dinámica de un cilindro inhomogéneo que rueda sobre un plano inclinado hasta despegarse del mismo.[12]​ Puesto que la velocidad es siempre tangente a la trayectoria, el vector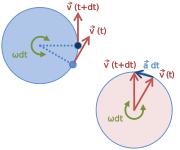La circunferencia a la derecha muestra la forma en que cambia la velocidad con el tiempo.Ya que los vectores de posición y velocidad giran conjuntamente, el período T (tiempo empleado en una vuelta completa) será el mismo en ambos casos.Comparando la trayectoria (izquierda) con su hodógrafa (derecha), se deduce que la aceleración apunta hacia el centro de la circunferencia, en forma opuesta al vector, se podrá notar el hecho de que estos últimos efectivamente apuntan hacia el centro.En mecánica relativista el cociente entre la fuerza centrípeta y la aceleración centrípeta, es diferente del cociente entre la fuerza tangencial y la aceleración tangencial.Esto introduce una diferencia fundamental con el caso newtoniano: la aceleración y la fuerza relativistas no son vectores necesariamente paralelos:De la relación anterior, se deduce que la fuerza y la aceleración sólo son paralelas en dos casos:El primer caso se da cuando la aceleración y la velocidad son perpendiculares, cosa que sucede por ejemplo el movimiento circular uniforme.En cualquier otro tipo de movimiento en general la fuerza y la aceleración no serán permanentemente paralelas.