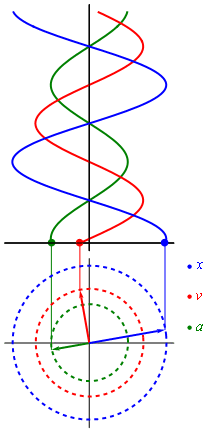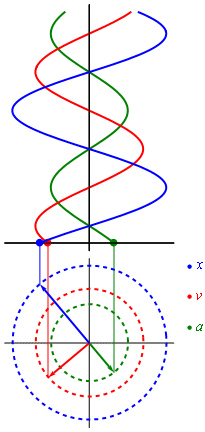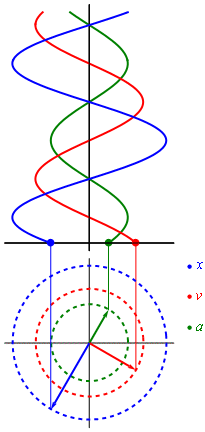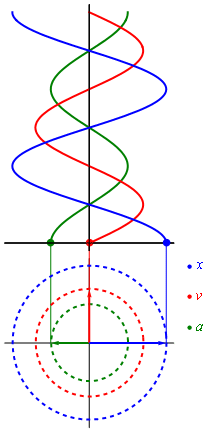
Movimiento armónico simple
En el caso de que la trayectoria sea rectilínea, la partícula que realiza un MAS oscila alejándose y acercándose de un punto situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide.
En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia este.
En este caso el cuerpo sube y baja.
En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacia la posición de equilibrio; esto es, en dirección contraria a su elongación (la «atrae» hacia la posición de equilibrio).
Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial: (1)
donde: Además, la frecuencia de oscilación puede escribirse como esto: (4)
La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión
La oscilación instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo: (5)
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional al desplazamiento: (11)
Un ejemplo, sería el que realiza un objeto unido al extremo de un muelle.
En ese caso k sería la constante de elasticidad del muelle.
Aplicando la segunda ley de newton tendríamos: (12)
Comparando esta ecuación y la que teníamos para la aceleración (6) se deduce: (13)
Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas.
En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza.
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad: (16)
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.
Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M172[1]) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
A partir de este dato, y conociendo la constante de fuerza del resorte unido a la silla, es posible entonces calcular la masa del individuo: (21)
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico.
En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:[2]
Sin embargo, puede una solución aproximada con las condiciones de contorno
donde: Una partícula de masa m sin espín sometida a un potencial cuadrático ejecuta en mecánica clásica un movimiento armónico simple, el equivalente cuántico de este movimiento, es el de una partícula sometida al potencial:
y las funciones de onda asociadas son: