Fricción
Se genera debido a las imperfecciones, que en mayor parte son microscópicas, entre las superficies en contacto,[cita requerida] aunque también existen fenómenos de interacción electrostática entre superficies.
Estas imperfecciones hacen que la fuerza perpendicular R entre ambas superficies no lo sea perfectamente, sino que forme un ángulo con la normal N (el ángulo de rozamiento).
En el rozamiento entre dos cuerpos se ha observado los siguientes hechos: El rozamiento puede variar en una medida mucho menor debido a otros factores: Algunos autores sintetizan las leyes del comportamiento de la fricción en los siguientes dos postulados básicos:[1] La segunda ley puede ilustrarse arrastrando un bloque sobre una superficie plana.
La fuerza de arrastre será la misma aunque el bloque descanse sobre la cara ancha o sobre un borde más angosto.
Estas leyes fueron establecidas primeramente por Leonardo da Vinci al final del siglo XV, olvidándose después durante largo tiempo; posteriormente fueron redescubiertas por el ingeniero francés Amontons en 1699.
La fuerza cinética, en cambio, es igual al coeficiente de rozamiento dinámico, denotado por la letra griega
No se tiene una idea perfectamente clara de la diferencia entre el rozamiento dinámico y el estático, pero se tiende a pensar que el estático es algo mayor que el dinámico, porque al permanecer en reposo ambas superficies pueden aparecer enlaces iónicos, o incluso microsoldaduras entre las superficies, factores que desaparecen en estado de movimiento.
Este fenómeno es tanto mayor cuanto más perfectas son las superficies.
Un caso más o menos común es el del gripaje de un motor por estar mucho tiempo parado (no solo se arruina por una temperatura muy elevada), ya que las superficies del pistón y la camisa, al permanecer en contacto y reposo durante largo tiempo, pueden llegar a soldarse entre sí.
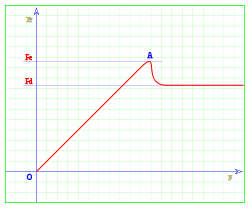
Como comprobación de lo anterior, se realiza el siguiente ensayo, sobre una superficie horizontal se coloca un cuerpo, y le aplica una fuerza horizontal F , muy pequeña en un principio, se puede ver que el cuerpo no se desplaza, la fuerza de rozamiento iguala a la fuerza aplicada y el cuerpo permanece en reposo, en la gráfica se representa en el eje horizontal la fuerza F aplicada, y en el eje vertical la fuerza de rozamiento Fr.
Entre los puntos O y A, ambas fuerzas son iguales y el cuerpo permanece estático; al sobrepasar el punto A el cuerpo súbitamente se comienza a desplazar, la fuerza ejercida en A es la máxima que el cuerpo puede soportar sin deslizarse, se denomina Fe o fuerza estática de fricción; la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado el desplazamiento es Fd o fuerza dinámica, es menor que la que fue necesaria para iniciarlo (Fe).
corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
El ángulo máximo en el que el objeto permanece en reposo se utiliza para calcular el coeficiente de fricción estática.
Este procedimiento se repite con diferentes combinaciones de materiales.
[2] Por otro lado, para calcular el coeficiente de fricción cinética, se comienza también con un ángulo pequeño y se aumenta hasta que el objeto empieza a moverse al aplicarle una pequeña perturbación externa.
con el plano tangente entre sólidos y el peso forma un ángulo
, la fuerza tractiz aplicada F horizontal máxima que se puede aplicar a un cuerpo en reposo es igual al coeficiente de rozamiento estático por su masa y por la aceleración de la gravedad.
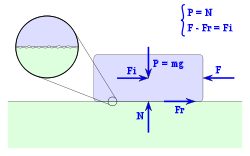
Dado un cuerpo en movimiento sobre una superficie horizontal, deben considerarse las siguientes fuerzas: Como equilibrio dinámico, se puede establecer que:
De esa misma expresión se deduce que la aceleración
, y sobre este plano inclinado se coloca un cuerpo con rozamiento, se tendrán tres fuerzas que intervienen: Si el cuerpo está en equilibrio, no se desliza, la suma vectorial de estas tres fuerzas es cero:
Lo que gráficamente sería un triángulo cerrado formado por estas tres fuerzas, puestas una a continuación de otra, como se ve en la figura.
El peso puede descomponerse en una componente normal al plano Pn y una componentes tangente al plano Pt y la ecuación anterior puede escribirse componente a componentes simplemente como: Dividiendo la primera componente entre la segunda se obtiene como resultado: El coeficiente de rozamiento estático es igual a la tangente del ángulo del plano inclinado, en el que el cuerpo se mantiene en equilibrio sin deslizar, ello permite calcular los distintos coeficientes de rozamiento, simplemente colocando un cuerpo de un material concreto sobre un plano inclinado del material con el que se pretende calcular su coeficiente de rozamiento, inclinando el plano progresivamente se observa el momento en el que el cuerpo comienza a deslizarse, la tangente de este ángulo es el valor del coeficiente de rozamiento.
teniendo en cuenta que: y como en el caso de equilibrio estático, se tiene: Con estas ecuaciones se determina las condiciones de equilibrio dinámico del cuerpo con fricción en un plano inclinado.
Si el cuerpo se desliza sin aceleración (a velocidad constante) su fuerza de inercia Fi será cero, y se puede ver que: esto es, de forma semejante al caso estático: Con lo que se puede decir que el coeficiente de rozamiento dinámico
Stribeck[3] demostró que a muy bajas velocidades predomina un rozamiento como el que ocurre entre dos superficies secas, y a velocidades muy altas predomina un rozamiento hidrodinámico.
La mínima fricción se alcanza para una velocidad intermedia dependiente de la presión del fluido, su "viscosidad cinemática".
En términos generales, es la resistencia de un líquido a fluir, comúnmente dicho, es su "espesor".
Todos los fluidos reales (excepto los superfluidos) tienen cierta resistencia a la tensión.
Por ejemplo, un magma de alta viscosidad creará un volcán alto, porque no se puede propagar hacia abajo con suficiente rapidez; la lava de baja viscosidad va a crear un volcán en escudo, que es grande y ancho.
Donde: Para un flujo unidimensional la anterior ecuación se reduce a la conocida expresión: