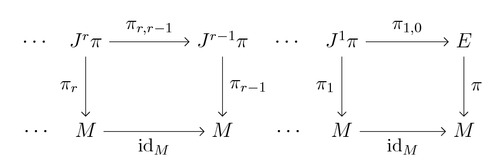
Haz de jets
Históricamente, los haces de jets se atribuyen a Ehresmann, y fueron un avance en el método (prolongación) de Élie Cartan, de tratar geométricamente con derivadas sucesivas, al imponer condiciones diferenciales a las variables formales recientemente introducidas.
Los haces de jets a veces se llaman espráis, aunque los espráis por lo general se refieren más específicamente al campo vectorial asociado inducido en el haz correspondiente (por ejemplo, el espray geodésico en variedades de Finsler).
En consecuencia, ahora se reconoce que el haz de jets es el dominio correcto para la teoría de campo covariante geométrica clásica, y se realiza mucho trabajo en las formulaciones de campos en la relatividad general que utilizan este enfoque.
Para p ∈ M, sea Γ(p) el conjunto de todas las secciones locales cuyo dominio contiene p. Se define I = (I(1), I(2), ..., I(m)) como una entidad multi indexada no ordenada (una m-tupla de enteros), tal que Defínanse las secciones locales σ, η ∈ Γ(p) que tienen el mismo r-jet en p si La relación de que dos aplicaciones tienen el mismo r-jet es una relación de equivalencia.
Sea σ una sección local de π con dominio W ⊂ M. La r-prolongación del jet de σ es la aplicación jrσ: W → Jr (π) definido por Téngase en cuenta que πr o jrσ = idW, por lo que jrσ realmente es una sección.
A continuación se da una construcción motivada independientemente del haz de secciones
el haz de gérmenes diferenciables que se anulan en
Entonces, cada vez que p ∈ M En consecuencia, la aplicación está bien definida y es claramente una función inyectiva.
El espacio de formas únicas diferenciables en Jr(π) se denota por
Una 1-forma general en J1(π) tiene la expresión Una sección σ en Γp(π) tiene una primera prolongación Por lo tanto, (j1σ) * θ se puede calcular como Esta expresión se anulará para todas las secciones σ si y solo si c = 0 y a = -bσ'(x).
En coordenadas locales, cada contacto de una forma en Jr+1(π) se puede escribir como una combinación lineal con coeficientes diferenciables
Téngase en cuenta que las formas de contacto en Jr+1(π) tienen órdenes r como máximo.
, es Un campo vectorial se llama horizontal si todos los coeficientes verticales desaparecen cuando
Un campo vectorial se llama vertical si todos los coeficientes horizontales desaparecen cuando ρi = 0.
Una sección se llama un campo vectorial en E con y ψ en Γ(TE).
Para (x, u, w) fijo, se identifica con las coordenadas con un elemento en el haz
Una sección es un campo vectorial en Jr(π), y se dice que
Una solución es una sección local σ ∈ W(π) que satisface
, para todo p en M. Considérese un ejemplo de una ecuación diferencial parcial de primer orden: Sea π el haz trivial (R 2 × R, pr1, R2) con coordenadas globales (x1, x' '2, u1).
Entonces la aplicación F: J1 (π) → R definida por da lugar a la ecuación diferencial que se puede escribir como En particular tiene una primera prolongación dada por y es una solución de esta ecuación diferencial, porque y entonces
satisface estas ecuaciones, Vr se denomina r-ésima prolongación de V a un campo vectorial en Jr(π).
Estos resultados se entienden mejor cuando se aplican a un ejemplo particular: Considérese el caso (E, π, M), donde E ≅ R2 y M ≃ R. Entonces, (J1(π), π, E) define el primer haz del jet, y puede ser coordenado por (x, u, u1), donde para todos los p ∈ M y σ en Γp(π).
Por lo tanto, para la preservación del contacto ideal, se requiere que Y entonces la primera prolongación de V a un campo de vectores en J1(π) es Calculando también la segunda prolongación de V a un campo vectorial en J2(π), se tienen
Por lo tanto, el vector prolongado tiene la forma Las formas de contacto son Para preservar el contacto ideal, se requiere Ahora, θ no tiene dependencia de u2.
Por lo tanto, a partir de esta ecuación se deduce la fórmula para ρ, que necesariamente será el mismo resultado encontrado para V1.
da lugar al "espacio de jets infinito J∞(π).
, que nace como un límite directo, tiene una estructura adicional: es un álgebra conmutativa filtrada.
, por lo que es una función suave en variedad de dimensión finita Jk (π) en el sentido habitual.
que ahora se cierra bajo la operación de poseer derivada total.
Sin embargo, esta restricción no simplifica la teoría, ya que la trivialidad global de π no implica la trivialidad global de π1.