

En topología , la teoría de nudos es el estudio de nudos matemáticos . Si bien está inspirado en nudos que aparecen en la vida cotidiana, como los de los cordones de los zapatos y las cuerdas, un nudo matemático se diferencia en que los extremos están unidos de modo que no se pueden deshacer, siendo el nudo más simple un anillo (o " desanudado "). En lenguaje matemático, un nudo es la incrustación de un círculo en un espacio euclidiano tridimensional . Dos nudos matemáticos son equivalentes si uno puede transformarse en el otro mediante una deformación sobre sí mismo (conocida como isotopía ambiental ); estas transformaciones corresponden a manipulaciones de una cuerda anudada que no implican cortarla ni pasarla por sí misma.
Los nudos se pueden describir de varias maneras. Utilizando diferentes métodos de descripción, puede haber más de una descripción de un mismo nudo. Por ejemplo, un método común para describir un nudo es un diagrama plano llamado diagrama de nudos, en el que cualquier nudo se puede dibujar de muchas maneras diferentes. Por tanto, un problema fundamental en la teoría de nudos es determinar cuándo dos descripciones representan el mismo nudo.
Existe una solución algorítmica completa a este problema, que tiene una complejidad desconocida . [ cita necesaria ] En la práctica, los nudos a menudo se distinguen utilizando una invariante de nudo , una "cantidad" que es la misma cuando se calcula a partir de diferentes descripciones de un nudo. Los invariantes importantes incluyen polinomios de nudos , grupos de nudos e invariantes hiperbólicas.
La motivación original de los fundadores de la teoría de nudos fue crear una tabla de nudos y eslabones , que son nudos de varios componentes entrelazados entre sí. Se han tabulado más de seis mil millones de nudos y eslabones desde los inicios de la teoría de nudos en el siglo XIX.
Para obtener más información, los matemáticos han generalizado el concepto de nudo de varias maneras. Los nudos se pueden considerar en otros espacios tridimensionales y se pueden utilizar objetos distintos de los círculos; ver nudo (matemáticas) . Por ejemplo, un nudo de dimensiones superiores es una esfera de n dimensiones incrustada en un espacio euclidiano de ( n +2) dimensiones.

Los arqueólogos han descubierto que hacer nudos se remonta a tiempos prehistóricos. Además de sus usos, como registrar información y unir objetos, los nudos han interesado a los humanos por su estética y simbolismo espiritual. Los nudos aparecen en diversas formas de obras de arte chinas que datan de varios siglos antes de Cristo (ver nudos chinos ). El nudo sin fin aparece en el budismo tibetano , mientras que los anillos borromeos han aparecido repetidas veces en diferentes culturas, representando a menudo la fuerza en la unidad. Los monjes celtas que crearon el Libro de Kells llenaron páginas enteras de intrincados nudos celtas .

Alexandre-Théophile Vandermonde desarrolló por primera vez una teoría matemática de los nudos en 1771, quien señaló explícitamente la importancia de las características topológicas al discutir las propiedades de los nudos relacionadas con la geometría de posición. Los estudios matemáticos de los nudos comenzaron en el siglo XIX con Carl Friedrich Gauss , quien definió la integral de enlace (Silver 2006). En la década de 1860, la teoría de Lord Kelvin de que los átomos eran nudos en el éter llevó a Peter Guthrie Tait a crear las primeras tablas de nudos para una clasificación completa. Tait, en 1885, publicó una tabla de nudos con hasta diez cruces, y lo que se conoció como las conjeturas de Tait . Este registro motivó a los primeros teóricos de nudos, pero la teoría de nudos finalmente se convirtió en parte del tema emergente de la topología .
Estos topólogos de principios del siglo XX ( Max Dehn , JW Alexander y otros) estudiaron los nudos desde el punto de vista del grupo de nudos y las invariantes de la teoría de la homología , como el polinomio de Alexander . Este sería el principal enfoque de la teoría de nudos hasta que una serie de avances transformaron el tema.
A finales de la década de 1970, William Thurston introdujo la geometría hiperbólica en el estudio de los nudos con el teorema de hiperbolización . Se demostró que muchos nudos eran hiperbólicos , lo que permitió el uso de la geometría para definir nuevas y poderosas invariantes de nudos . El descubrimiento del polinomio de Jones por Vaughan Jones en 1984 (Sossinsky 2002, pp. 71-89), y las contribuciones posteriores de Edward Witten , Maxim Kontsevich y otros, revelaron conexiones profundas entre la teoría de nudos y los métodos matemáticos en la mecánica estadística y el campo cuántico. teoría . Desde entonces se ha inventado una gran cantidad de invariantes de nudos, utilizando herramientas sofisticadas como grupos cuánticos y homología de Floer .
En las últimas décadas del siglo XX, los científicos se interesaron en estudiar los nudos físicos para comprender los fenómenos de nudos en el ADN y otros polímeros. La teoría de nudos se puede utilizar para determinar si una molécula es quiral (tiene "lateralidad") o no (Simon 1986). Los ovillos , cuerdas con ambos extremos fijados en su lugar, se han utilizado eficazmente para estudiar la acción de la topoisomerasa en el ADN (Flapan 2000). La teoría de nudos puede ser crucial en la construcción de computadoras cuánticas, a través del modelo de computación cuántica topológica (Collins 2006).
Un nudo se crea comenzando con un segmento de línea unidimensional , envolviéndolo alrededor de sí mismo arbitrariamente y luego fusionando sus dos extremos libres para formar un bucle cerrado (Adams 2004) (Sossinsky 2002). Simplemente, podemos decir que un nudo es una "curva cerrada simple" (ver Curva ), es decir: una función "casi" inyectiva y continua , siendo la única "no inyectividad" . Los topólogos consideran que los nudos y otros enredos, como eslabones y trenzas, son equivalentes si el nudo se puede empujar suavemente, sin cruzarse, para que coincida con otro nudo.
La idea de equivalencia de nudos es dar una definición precisa de cuándo dos nudos deben considerarse iguales incluso cuando están colocados de manera muy diferente en el espacio. Una definición matemática formal es que dos nudos son equivalentes si existe un homeomorfismo que preserva la orientación con .
Lo que significa esta definición de equivalencia de nudos es que dos nudos son equivalentes cuando existe una familia continua de homeomorfismos del espacio sobre sí mismo, de modo que el último de ellos lleva el primer nudo al segundo nudo. (En detalle: dos nudos y son equivalentes si existe un mapeo continuo tal que a) para cada uno, el mapeo que lleva a es un homeomorfismo de sobre sí mismo; b) para todos ; y C) . Esta función se conoce como isotopía ambiental ).
Estas dos nociones de equivalencia de nudos concuerdan exactamente sobre qué nudos son equivalentes: dos nudos que son equivalentes según la definición de homeomorfismo que preserva la orientación también son equivalentes según la definición de isotopía ambiental, porque cualquier homeomorfismo de hacia sí mismo que preserve la orientación es la etapa final de una isotopía ambiental a partir de la identidad. Por el contrario, dos nudos equivalentes según la definición de isotopía ambiental también son equivalentes según la definición de homeomorfismo que preserva la orientación, porque la etapa (final) de la isotopía ambiental debe ser un homeomorfismo que preserva la orientación que lleva un nudo al otro.
El problema básico de la teoría de nudos, el problema de reconocimiento , es determinar la equivalencia de dos nudos. Existen algoritmos para resolver este problema; el primero fue propuesto por Wolfgang Haken a finales de los años 1960 (Hass 1998). No obstante, estos algoritmos pueden consumir mucho tiempo y una cuestión importante en la teoría es comprender cuán difícil es realmente este problema (Hass 1998). El caso especial de reconocer el desanudado , llamado problema del desanudado , es de particular interés (Hoste 2005). En febrero de 2021, Marc Lackenby anunció un nuevo algoritmo de reconocimiento de nudos que se ejecuta en tiempo cuasi polinómico . [1]

Una forma útil de visualizar y manipular nudos es proyectar el nudo en un plano; piense en el nudo proyectando una sombra en la pared. Un pequeño cambio en la dirección de la proyección asegurará que sea uno a uno excepto en los puntos dobles, llamados cruces , donde la "sombra" del nudo se cruza una vez transversalmente (Rolfsen 1976). En cada cruce, para poder recrear el nudo original, es necesario distinguir el hilo superior del hilo inferior. Esto a menudo se hace creando una ruptura en el hilo que va debajo. El diagrama resultante es una curva plana sumergida con el dato adicional de qué hilo está por encima y cuál por debajo en cada cruce. (Estos diagramas se denominan diagramas de nudos cuando representan un nudo y diagramas de vínculos cuando representan un vínculo ). De manera análoga, las superficies anudadas en 4 espacios se pueden relacionar con superficies sumergidas en 3 espacios.
Un diagrama reducido es un diagrama de nudos en el que no hay cruces reducibles (también cruces nugatorios o removibles ), o en el que se han eliminado todos los cruces reducibles. [2] [3] Una proyección de pétalos es un tipo de proyección en la que, en lugar de formar puntos dobles, todas las hebras del nudo se encuentran en un único punto de cruce, conectado a él mediante bucles que forman "pétalos" no anidados. [4]
En 1927, trabajando con esta forma esquemática de nudos, JW Alexander y Garland Baird Briggs, e independientemente Kurt Reidemeister , demostraron que dos diagramas de nudos que pertenecen al mismo nudo pueden relacionarse mediante una secuencia de tres tipos de movimientos en el diagrama, como se muestra a continuación. . Estas operaciones, ahora llamadas movimientos de Reidemeister , son:
La prueba de que los diagramas de nudos equivalentes están conectados mediante movimientos de Reidemeister se basa en un análisis de lo que sucede bajo la proyección plana del movimiento que lleva de un nudo a otro. El movimiento se puede organizar de modo que casi todo el tiempo la proyección sea un diagrama de nudos, excepto en un número finito de momentos en los que ocurre un "evento" o "catástrofe", como cuando más de dos hilos se cruzan en un punto o múltiples hilos. volverse tangente en un punto. Una inspección minuciosa mostrará que los eventos complicados pueden eliminarse, dejando sólo los más simples: (1) una "torcedura" que se forma o se endereza; (2) dos hilos que se vuelven tangentes en un punto y lo atraviesan; y (3) tres hilos que se cruzan en un punto. Estos son precisamente los movimientos de Reidemeister (Sossinsky 2002, cap. 3) (Lickorish 1997, cap. 1).

Una invariante de nudo es una "cantidad" que es la misma para nudos equivalentes (Adams 2004) (Lickorish 1997) (Rolfsen 1976). Por ejemplo, si el invariante se calcula a partir de un diagrama de nudos, debería dar el mismo valor para dos diagramas de nudos que representen nudos equivalentes. Un invariante puede tomar el mismo valor en dos nudos diferentes, por lo que por sí solo puede ser incapaz de distinguir todos los nudos. Una invariante elemental es la tricolorabilidad .
Los invariantes de nudos "clásicos" incluyen el grupo de nudos , que es el grupo fundamental del complemento de nudos , y el polinomio de Alexander , que puede calcularse a partir del invariante de Alexander, un módulo construido a partir de la cobertura cíclica infinita del complemento de nudos (Lickorish 1997) (Rolfsen 1976). A finales del siglo XX, se descubrieron invariantes como los polinomios de nudos "cuánticos", los invariantes de Vassiliev y los invariantes hiperbólicos. Estas invariantes antes mencionadas son sólo la punta del iceberg de la teoría de nudos moderna.
Un polinomio de nudo es una invariante de nudo que es un polinomio . Ejemplos bien conocidos incluyen los polinomios de Jones y Alexander . Una variante del polinomio de Alexander, el polinomio de Alexander-Conway , es un polinomio en la variable z con coeficientes enteros (Lickorish 1997).
El polinomio de Alexander-Conway en realidad se define en términos de enlaces , que consisten en uno o más nudos entrelazados entre sí. Los conceptos explicados anteriormente para nudos, p. ej. diagramas y movimientos de Reidemeister, también son válidos para enlaces.
Considere un diagrama de enlace orientado, es decir, uno en el que cada componente del enlace tiene una dirección preferida indicada por una flecha. Para un cruce dado del diagrama, sean los diagramas de enlaces orientados resultantes de cambiar el diagrama como se indica en la figura:

El diagrama original podría ser o , dependiendo de la configuración del cruce elegido. Entonces el polinomio de Alexander-Conway , se define recursivamente según las reglas:
La segunda regla es lo que a menudo se denomina relación de madeja . Para comprobar que estas reglas dan una invariante de un enlace orientado, se debe determinar que el polinomio no cambia bajo los tres movimientos de Reidemeister. De esta manera se pueden definir muchos polinomios de nudos importantes.
El siguiente es un ejemplo de un cálculo típico utilizando una relación de madeja. Calcula el polinomio de Alexander-Conway del nudo trébol . Las manchas amarillas indican dónde se aplica la relación.
da el desanudado y el enlace de Hopf . Aplicando la relación al enlace Hopf donde se indica,
da un vínculo deformable a uno con 0 cruces (en realidad es el desvío de dos componentes) y un desanudado. La desvinculación requiere un poco de astucia:
lo que implica que C (desvinculación de dos componentes) = 0, ya que los dos primeros polinomios son desanudados y por tanto iguales.
Poniendo todo esto junto se mostrará:
Dado que el polinomio de Alexander-Conway es un invariante de nudo, esto muestra que el trébol no es equivalente al desanudado. Entonces el trébol realmente está "anudado".
En realidad, hay dos nudos de trébol, llamados tréboles derecho e izquierdo, que son imágenes especulares entre sí (tome un diagrama del trébol que se muestra arriba y cambie cada cruce hacia el otro lado para obtener la imagen especular). Estos no son equivalentes entre sí, lo que significa que no son anfiquirales. Esto fue demostrado por Max Dehn , antes de la invención de los polinomios de nudos, utilizando métodos teóricos de grupos (Dehn 1914). Pero el polinomio de Alexander-Conway de cada tipo de trébol será el mismo, como se puede ver al realizar el cálculo anterior con la imagen especular. De hecho, el polinomio de Jones puede distinguir entre nudos de trébol diestros y zurdos (Lickorish 1997).
William Thurston demostró que muchos nudos son nudos hiperbólicos , lo que significa que el complemento del nudo (es decir, el conjunto de puntos del espacio tridimensional que no están en el nudo) admite una estructura geométrica, en particular la de geometría hiperbólica . La estructura hiperbólica depende sólo del nudo, por lo que cualquier cantidad calculada a partir de la estructura hiperbólica es una invariante del nudo (Adams 2004).
La geometría nos permite visualizar cómo se ve el interior de un nudo o complemento de eslabón imaginando rayos de luz viajando a lo largo de las geodésicas de la geometría. Un ejemplo lo proporciona la imagen del complemento de los anillos borromeos . El habitante de este complemento de enlace está viendo el espacio desde cerca del componente rojo. Las bolas de la imagen son vistas de los barrios de horoball del enlace. Al engrosar el enlace de forma estándar, se obtienen las vecindades horoball de los componentes del enlace. Aunque el límite de una vecindad es un toroide, visto desde dentro del complemento del enlace, parece una esfera. Cada componente del enlace aparece como infinitas esferas (de un color) ya que hay infinitos rayos de luz desde el observador hasta el componente del enlace. El paralelogramo fundamental (que se indica en la imagen), se mosaico tanto vertical como horizontalmente y muestra cómo extender el patrón de esferas infinitamente.
Este patrón, el patrón horoball, es en sí mismo un invariante útil. Otras invariantes hiperbólicas incluyen la forma del paralelogramo fundamental, la longitud de la geodésica más corta y el volumen. Los esfuerzos modernos de tabulación de nudos y enlaces han utilizado estas invariantes de manera efectiva. Las computadoras rápidas y los métodos inteligentes para obtener estas invariantes hacen que calcularlas, en la práctica, sea una tarea sencilla (Adams, Hildebrand y Weeks 1991).
Un nudo en tres dimensiones se puede desatar cuando se coloca en un espacio de cuatro dimensiones. Esto se hace cambiando los cruces. Supongamos que una hebra está detrás de otra vista desde un punto elegido. Levántelo a la cuarta dimensión, para que no haya ningún obstáculo (el hilo frontal no tiene ningún componente allí); luego deslízalo hacia adelante y déjalo caer hacia atrás, ahora al frente. Las analogías con el avión serían levantar una cuerda de la superficie o quitar un punto del interior de un círculo.
De hecho, en cuatro dimensiones, cualquier bucle cerrado de cuerda unidimensional que no se cruce es equivalente a un nudo. Primero "empuje" el bucle hacia un subespacio tridimensional, lo cual siempre es posible, aunque técnico, de explicar.
Sin embargo, el espacio de cuatro dimensiones ocurre en la teoría clásica de nudos, y un tema importante es el estudio de los nudos cortados y los nudos de cinta . Un problema notorio y abierto es si cada nudo cortado es también una cinta.
Dado que un nudo puede considerarse topológicamente como una esfera unidimensional, la siguiente generalización es considerar una esfera bidimensional ( ) incrustada en un espacio euclidiano de 4 dimensiones ( ). Tal incrustación está anudada si no hay un homeomorfismo sobre sí mismo, llevando las 2 esferas incrustadas a la incrustación "redonda" estándar de las 2 esferas. Los nudos suspendidos y los nudos hilados son dos familias típicas de este tipo de nudos de dos esferas.
La técnica matemática llamada "posición general" implica que para una n -esfera dada en un espacio euclidiano de m dimensiones, si m es lo suficientemente grande (dependiendo de n ), la esfera debe estar sin nudos. En general, las n -esferas lineales por tramos forman nudos sólo en el espacio ( n + 2)-dimensional (Zeeman 1963), aunque esto ya no es un requisito para esferas suavemente anudadas. De hecho, hay esferas suavemente anudadas en un espacio de 6 k dimensiones; por ejemplo, hay tres esferas suavemente anudadas en (Haefliger 1962) (Levine 1965). Así, la codimensión de un nudo liso puede ser arbitrariamente grande cuando no se fija la dimensión de la esfera anudada; sin embargo, cualquier k -esfera lisa incrustada en ella no está anudada. La noción de nudo tiene más generalizaciones en matemáticas, ver: Nudo (matemáticas) , clasificación isotópica de incrustaciones .
Cada nudo en la n -esfera es el vínculo de un conjunto algebraico real con singularidad aislada en (Akbulut & King 1981).
Un nudo n es un nudo único incrustado en . Un enlace n consta de k copias de elementos incrustados , donde k es un número natural . Tanto el como los casos están bien estudiados, y el caso también. [5] [6]

Se pueden añadir dos nudos cortando ambos nudos y uniendo los pares de extremos. La operación se llama suma de nudos o, a veces, suma o composición conexa de dos nudos. Esto se puede definir formalmente de la siguiente manera (Adams 2004): considere una proyección plana de cada nudo y suponga que estas proyecciones son disjuntas. Encuentra un rectángulo en el plano donde un par de lados opuestos son arcos a lo largo de cada nudo mientras que el resto del rectángulo está separado de los nudos. Forme un nuevo nudo eliminando el primer par de lados opuestos y uniendo el otro par de lados opuestos. El nudo resultante es una suma de los nudos originales. Dependiendo de cómo se haga esto, pueden resultar dos nudos diferentes (pero no más). Esta ambigüedad en la suma se puede eliminar considerando que los nudos estén orientados , es decir, que tengan una dirección de desplazamiento preferida a lo largo del nudo, y que requieran que los arcos de los nudos en la suma estén orientados consistentemente con el límite orientado del rectángulo.
La suma de nudos de nudos orientados es conmutativa y asociativa . Un nudo es primo si no es trivial y no puede escribirse como la suma de dos nudos no triviales. Un nudo que puede escribirse como tal suma es compuesto . Existe una descomposición prima para los nudos, análoga a la de los números primos y compuestos (Schubert 1949). Para nudos orientados, esta descomposición también es única. También se pueden agregar nudos de dimensiones mayores, pero existen algunas diferencias. Si bien no se puede desatar el nudo en tres dimensiones agregando dos nudos no triviales, se puede hacerlo en dimensiones más altas, al menos cuando se consideran nudos lisos en codimensión al menos 3.
Los nudos también se pueden construir utilizando el enfoque de topología de circuitos . Esto se hace combinando unidades básicas llamadas contactos suaves usando cinco operaciones (paralela, serie, cruzada, concertada y secundaria). [7] [8] El enfoque es aplicable también a cadenas abiertas y también puede ampliarse para incluir los llamados contactos duros.
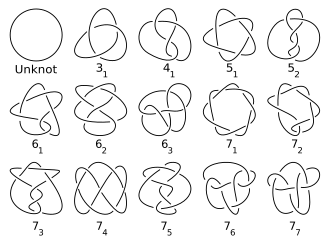
Tradicionalmente los nudos se han catalogado en función del número de cruce . Las tablas de nudos generalmente incluyen sólo nudos principales y sólo una entrada para un nudo y su imagen especular (incluso si son diferentes) (Hoste, Thistlethwaite y Weeks 1998). El número de nudos no triviales de un número de cruce determinado aumenta rápidamente, lo que dificulta computacionalmente la tabulación (Hoste 2005, p. 20). Los esfuerzos de tabulación han logrado enumerar más de 6 mil millones de nudos y enlaces (Hoste 2005, p. 28). La secuencia del número de nudos primos de un número de cruce dado, hasta el número de cruce 16, es 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988,46 972 ,253 293 ,1 388 705 ... (secuencia A002863 en la OEIS ). Si bien se conocen los límites exponenciales superior e inferior de esta secuencia, no se ha demostrado que esta secuencia sea estrictamente creciente (Adams 2004).
Las primeras tablas de nudos de Tait, Little y Kirkman utilizaron diagramas de nudos, aunque Tait también utilizó un precursor de la notación Dowker . Se han inventado diferentes notaciones para los nudos que permiten una tabulación más eficiente (Hoste 2005).
Las primeras tablas intentaron enumerar todos los nudos de como máximo 10 cruces y todos los nudos alternos de 11 cruces (Hoste, Thistlethwaite y Weeks 1998). El desarrollo de la teoría de nudos debido a Alexander, Reidemeister, Seifert y otros facilitó la tarea de verificación y Alexander-Briggs y Reidemeister publicaron tablas de nudos de hasta 9 cruces a finales de la década de 1920.
La primera verificación importante de este trabajo fue realizada en la década de 1960 por John Horton Conway , quien no sólo desarrolló una nueva notación sino también el polinomio de Alexander-Conway (Conway 1970) (Doll y Hoste 1991). Se verificó la lista de nudos de como máximo 11 cruces y una nueva lista de enlaces de hasta 10 cruces. Conway encontró varias omisiones pero sólo una duplicación en las tablas Tait-Little; sin embargo, se perdió los duplicados llamados el par Perko , que sólo serían notados en 1974 por Kenneth Perko (Perko 1974). Este famoso error se propagaría cuando Dale Rolfsen añadió una tabla de nudos en su influyente texto, basado en el trabajo de Conway. El artículo de Conway de 1970 sobre la teoría de nudos también contiene una duplicación tipográfica en su página de 11 nudos cruzados no alternos y omite cuatro ejemplos: dos enumerados anteriormente en la tesis senior de Princeton de 1968 de D. Lombardero y dos más descubiertos posteriormente por Alain Caudron. [ver Perko (1982), Primalidad de ciertos nudos, Procedimientos de topología] Menos famoso es el duplicado en su tabla de 10 enlaces cruzados: 2.-2.-20.20 es el espejo de 8*-20:-20. [Ver Perko (2016), Aspectos destacados históricos de la teoría de nudos no cíclicos, J. Knot Theory Ramifications].
A finales de la década de 1990, Hoste, Thistlethwaite y Weeks tabularon todos los nudos a través de 16 cruces (Hoste, Thistlethwaite y Weeks 1998). En 2003, Rankin, Flint y Schermann tabularon los nudos alternos a través de 22 cruces (Hoste 2005). En 2020, Burton tabuló todos los nudos principales con hasta 19 cruces (Burton 2020).
Esta es la notación más tradicional, debido al artículo de 1927 de James W. Alexander y Garland B. Briggs y posteriormente ampliado por Dale Rolfsen en su tabla de nudos (ver imagen arriba y Lista de nudos principales ). La notación simplemente organiza los nudos por su número de cruce. Se escribe el número de cruce con un subíndice para indicar su orden entre todos los nudos con ese número de cruce. Este orden es arbitrario y, por tanto, no tiene ningún significado especial (aunque en cada número de cruces el nudo torcido viene después del nudo toroidal ). Los enlaces se escriben por el número de cruce con un superíndice para indicar el número de componentes y un subíndice para indicar su orden dentro de los enlaces con el mismo número de componentes y cruces. Así, el nudo trébol se anota como 3 1 y el enlace de Hopf es 2.2
1. Los nombres de Alexander-Briggs en el rango 10 162 a 10 166 son ambiguos, debido al descubrimiento del par Perko en las tablas de nudos originales y posteriores de Charles Newton Little , y a las diferencias en el enfoque para corregir este error en las tablas de nudos y otras publicaciones creadas. después de este punto. [9]

La notación Dowker-Thistlethwaite , también llamada notación o código de Dowker, para un nudo es una secuencia finita de números enteros pares. Los números se generan siguiendo el nudo y marcando los cruces con números enteros consecutivos. Dado que cada cruce se visita dos veces, esto crea un emparejamiento de números enteros pares con números enteros impares. Se coloca una señal adecuada para indicar el cruce por encima y por debajo. Por ejemplo, en esta figura el diagrama de nudos tiene cruces etiquetados con los pares (1,6) (3,−12) (5,2) (7,8) (9,−4) y (11,−10). La notación de Dowker-Thistlethwaite para este etiquetado es la secuencia: 6, −12, 2, 8, −4, −10. Un diagrama de nudos tiene más de una notación Dowker posible y existe una ambigüedad bien entendida al reconstruir un nudo a partir de una notación Dowker-Thistlethwaite.
La notación de Conway para nudos y eslabones, que lleva el nombre de John Horton Conway , se basa en la teoría de los enredos (Conway 1970). La ventaja de esta notación es que refleja algunas propiedades del nudo o eslabón.
La notación describe cómo construir un diagrama de enlace particular del enlace. Comience con un poliedro básico , un gráfico plano conectado de 4 valencias sin regiones digón . Un poliedro de este tipo se indica primero por el número de vértices y luego por un número de asteriscos que determinan la posición del poliedro en una lista de poliedros básicos. Por ejemplo, 10** denota el segundo poliedro de 10 vértices en la lista de Conway.
Luego, cada vértice tiene una maraña algebraica sustituida (cada vértice está orientado, por lo que no hay elección arbitraria en la sustitución). Cada uno de estos enredos tiene una notación que consta de números y signos + o −.
Un ejemplo es 1*2 −3 2. El 1* denota el único poliedro básico de 1 vértice. El 2 −3 2 es una secuencia que describe la fracción continua asociada a un nudo racional . Se inserta esta maraña en el vértice del poliedro básico 1*.
Un ejemplo más complicado es 8*3.1.2 0.1.1.1.1.1 Aquí nuevamente 8* se refiere a un poliedro básico con 8 vértices. Los puntos separan la notación de cada enredo.
Cualquier enlace admite tal descripción, y está claro que se trata de una notación muy compacta incluso para números de cruce muy grandes. Generalmente se utilizan algunas taquigrafías adicionales. El último ejemplo generalmente se escribe 8*3:2 0, donde se omiten los unos y se mantiene el número de puntos excepto los puntos al final. Para un nudo algebraico como el del primer ejemplo, a menudo se omite 1*.
El artículo pionero de Conway sobre el tema enumera poliedros básicos de hasta 10 vértices que utiliza para tabular enlaces, que se han convertido en estándar para esos enlaces. Para obtener una lista adicional de poliedros de vértices superiores, hay opciones no estándar disponibles.
El código Gauss , similar a la notación Dowker-Thistlethwaite, representa un nudo con una secuencia de números enteros. Sin embargo, en lugar de que cada cruce esté representado por dos números diferentes, los cruces están etiquetados con un solo número. Cuando el cruce es un cruce excesivo, se enumera un número positivo. En un cruce inferior, un número negativo. Por ejemplo, el nudo trébol en código Gauss se puede dar como: 1,−2,3,−1,2,−3
El código Gauss tiene una capacidad limitada para identificar nudos. Este problema se soluciona parcialmente con el código Gauss extendido .
Hay varias introducciones a la teoría de nudos. Una introducción clásica para estudiantes de posgrado o estudiantes universitarios avanzados es (Rolfsen 1976). Otros buenos textos de las referencias son (Adams 2004) y (Lickorish 1997). Adams es informal y accesible en su mayor parte para los estudiantes de secundaria. Lickorish es una introducción rigurosa para estudiantes de posgrado, que cubre una buena combinación de temas clásicos y modernos. (Cromwell 2004) es adecuado para estudiantes universitarios que conocen la topología de conjuntos de puntos; No se requieren conocimientos de topología algebraica.