Mediana

Cuantil medio de un conjunto de datos o distribución de probabilidad

Cálculo de la mediana en conjuntos de datos de observaciones impares (arriba) y pares (abajo)

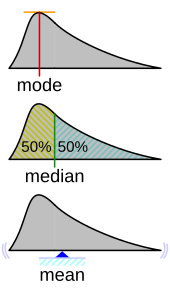
La mediana de un conjunto de números es el valor que separa la mitad superior de la mitad inferior de una muestra de datos , una población o una distribución de probabilidad . Para un conjunto de datos , puede considerarse como el valor "medio". La característica básica de la mediana al describir los datos en comparación con la media (a menudo descrita simplemente como el "promedio") es que no está sesgada por una pequeña proporción de valores extremadamente grandes o pequeños y, por lo tanto, proporciona una mejor representación del centro. La mediana de ingresos , por ejemplo, puede ser una mejor manera de describir el centro de la distribución de ingresos porque los aumentos en los ingresos más altos por sí solos no tienen efecto sobre la mediana. Por esta razón, la mediana es de importancia central en las estadísticas robustas .

Conjunto finito de números

La mediana de una lista finita de números es el número "medio", cuando esos números se enumeran en orden del más pequeño al más grande.

Si el conjunto de datos tiene un número impar de observaciones, se selecciona la del medio (después de ordenarlas en orden ascendente). Por ejemplo, la siguiente lista de siete números:

1, 3, 3, 6 , 7, 8, 9

tiene una mediana de 6 , que es el cuarto valor.

Si el conjunto de datos tiene un número par de observaciones, no hay un valor medio definido y la mediana suele definirse como la media aritmética de los dos valores medios. ^{[1] [2]} Por ejemplo, este conjunto de datos de 8 números

1, 2, 3, 4, 5 , 6, 8, 9

tiene un valor medio de 4,5 , es decir (en términos más técnicos, esto interpreta la mediana como el rango medio completamente recortado ). ${\displaystyle (4+5)/2}$

En general, con esta convención, la mediana se puede definir de la siguiente manera: Para un conjunto de datos de elementos, ordenados del menor al mayor, ${\displaystyle x}$ ${\displaystyle n}$

Si es impar, ${\displaystyle n}$ ${\displaystyle \operatorname {med} (x)=x_{(n+1)/2}}$

Si es par, ${\displaystyle n}$ ${\displaystyle \operatorname {med} (x)={\frac {x_{(n/2)}+x_{((n/2)+1)}}{2}}}$

Definición y notación

Formalmente, la mediana de una población es cualquier valor tal que al menos la mitad de la población sea menor o igual a la mediana propuesta y al menos la mitad sea mayor o igual a la mediana propuesta. Como se vio anteriormente, las medianas pueden no ser únicas. Si cada conjunto contiene más de la mitad de la población, entonces una parte de la población es exactamente igual a la mediana única.

La mediana está bien definida para cualquier dato ordenado (unidimensional) y es independiente de cualquier métrica de distancia . Por lo tanto, la mediana se puede aplicar a clases escolares que están clasificadas pero no son numéricas (por ejemplo, calcular una calificación mediana cuando las calificaciones de los exámenes de los estudiantes se califican de F a A), aunque el resultado podría estar a medio camino entre las clases si hay un número par de clases. (Para las clases con números impares, se determina una clase específica como la mediana).

Por otra parte, una mediana geométrica se define en cualquier número de dimensiones. Un concepto relacionado, en el que el resultado se ve obligado a corresponder a un miembro de la muestra, es el medoide .

No existe una notación estándar ampliamente aceptada para la mediana, pero algunos autores representan la mediana de una variable x como med( x ), x͂ , ^[3] como μ _1/2 , ^[1] o como M . ^{[3] [4]} En cualquiera de estos casos, el uso de estos u otros símbolos para la mediana debe definirse explícitamente cuando se introducen.

La mediana es un caso especial de otras formas de resumir los valores típicos asociados con una distribución estadística : es el segundo cuartil , el quinto decil y el percentil 50 .

Usos

La mediana se puede utilizar como medida de ubicación cuando se concede poca importancia a los valores extremos, normalmente porque una distribución está sesgada , los valores extremos no se conocen o los valores atípicos no son confiables, es decir, pueden ser errores de medición o transcripción.

Por ejemplo, considere el multiconjunto

1, 2, 2, 2, 3, 14.

En este caso, la mediana es 2, al igual que la moda , y podría considerarse una mejor indicación del centro que la media aritmética de 4, que es mayor que todos los valores menos uno. Sin embargo, la relación empírica ampliamente citada de que la media se desplaza "más hacia la cola" de una distribución que la mediana no es generalmente cierta. Como máximo, se puede decir que las dos estadísticas no pueden estar "demasiado alejadas"; véase § Desigualdad que relaciona medias y medianas más abajo. ^[5]

Como la mediana se basa en los datos intermedios de un conjunto, no es necesario conocer el valor de los resultados extremos para calcularla. Por ejemplo, en una prueba de psicología que investiga el tiempo necesario para resolver un problema, si un pequeño número de personas no logra resolverlo en absoluto en el tiempo dado, aún se puede calcular una mediana. ^[6]

Debido a que la mediana es fácil de entender y calcular, y además es una aproximación robusta a la media , la mediana es una estadística de resumen popular en las estadísticas descriptivas . En este contexto, existen varias opciones para medir la variabilidad : el rango , el rango intercuartil , la desviación absoluta media y la desviación absoluta mediana .

Para fines prácticos, las diferentes medidas de localización y dispersión se comparan a menudo sobre la base de lo bien que se pueden estimar los valores poblacionales correspondientes a partir de una muestra de datos. La mediana, estimada utilizando la mediana de la muestra, tiene buenas propiedades en este sentido. Si bien no suele ser óptima si se supone una distribución poblacional dada, sus propiedades siempre son razonablemente buenas. Por ejemplo, una comparación de la eficiencia de los estimadores candidatos muestra que la media de la muestra es estadísticamente más eficiente cuando, y solo cuando, los datos no están contaminados por datos de distribuciones de cola pesada o de mezclas de distribuciones. ^{[ cita requerida ]} Incluso entonces, la mediana tiene una eficiencia del 64% en comparación con la media de varianza mínima (para muestras normales grandes), lo que significa que la varianza de la mediana será ~50% mayor que la varianza de la media. ^{[7] [8]}

Distribuciones de probabilidad

Para cualquier distribución de probabilidad de valor real con función de distribución acumulativa F , una mediana se define como cualquier número real  m que satisface las desigualdades (cf. el dibujo en la definición de valor esperado para variables aleatorias arbitrarias de valor real ). Una redacción equivalente utiliza una variable aleatoria X distribuida según F :   $${\displaystyle \lim _{x\to m-}F(x)\leq {\frac {1}{2}}\leq F(m)}$$ $${\displaystyle \operatorname {P} (X\leq m)\geq {\frac {1}{2}}{\text{ and }}\operatorname {P} (X\geq m)\geq {\frac {1}{2}}\,.}$$

Moda , mediana y media ( valor esperado ) de una función de densidad de probabilidad ^[9]

Nótese que esta definición no requiere que X tenga una distribución absolutamente continua (que tiene una función de densidad de probabilidad f ), ni requiere una discreta . En el primer caso, las desigualdades se pueden actualizar a igualdad: una mediana satisface y $${\displaystyle \operatorname {P} (X\leq m)=\int _{-\infty }^{m}{f(x)\,dx}={\frac {1}{2}}}$$ $${\displaystyle \operatorname {P} (X\geq m)=\int _{m}^{\infty }{f(x)\,dx}={\frac {1}{2}}\,.}$$

Cualquier distribución de probabilidad en el conjunto de números reales tiene al menos una mediana, pero en casos patológicos puede haber más de una mediana: si F es constante 1/2 en un intervalo (de modo que f = 0 allí), entonces cualquier valor de ese intervalo es una mediana. ${\displaystyle \mathbb {R} }$

Medianas de distribuciones particulares

Las medianas de ciertos tipos de distribuciones se pueden calcular fácilmente a partir de sus parámetros; además, existen incluso para algunas distribuciones que carecen de una media bien definida, como la distribución de Cauchy :

• La mediana de una distribución unimodal simétrica coincide con la moda.
• La mediana de una distribución simétrica que posee una media μ también toma el valor μ .
  • La mediana de una distribución normal con media μ y varianza σ ² es μ. De hecho, para una distribución normal, media = mediana = moda.
  • La mediana de una distribución uniforme en el intervalo [ a ,  b ] es ( a  +  b ) / 2, que también es la media.
• La mediana de una distribución de Cauchy con parámetro de ubicación x ₀ y parámetro de escala y es  x ₀ , el parámetro de ubicación.
• La mediana de una distribución de ley de potencia x ^{− a} , con exponente a  > 1 es 2 ^{1/( a  − 1)} x _min , donde x _min es el valor mínimo para el cual se cumple la ley de potencia ^[10]
• La mediana de una distribución exponencial con parámetro de velocidad λ es el logaritmo natural de 2 dividido por el parámetro de velocidad: λ ⁻¹ ln 2.
• La mediana de una distribución de Weibull con parámetro de forma k y parámetro de escala λ es  λ (ln 2) ^{1/ k} .

Propiedades

Propiedad de optimalidad

El error absoluto medio de una variable real c con respecto a la variable aleatoria  X es

${\displaystyle E(\left|X-c\right|)\,}$

Siempre que la distribución de probabilidad de X sea tal que exista la expectativa anterior, entonces m es una mediana de X si y solo si m es un minimizador del error absoluto medio con respecto a X. ^[11] En particular, si m es una mediana de muestra , entonces minimiza la media aritmética de las desviaciones absolutas. ^[12] Nótese, sin embargo, que en los casos donde la muestra contiene un número par de elementos, este minimizador no es único.

De manera más general, una mediana se define como un mínimo de

${\displaystyle E(|X-c|-|X|),}$

como se analiza más adelante en la sección sobre medianas multivariadas (específicamente, la mediana espacial ).

Esta definición de la mediana basada en la optimización es útil en el análisis de datos estadísticos, por ejemplo, en la agrupación de k -medianas .

Desigualdad que relaciona medias y medianas

Comparación de la media , la mediana y la moda de dos distribuciones log-normales con diferente asimetría

Si la distribución tiene varianza finita, entonces la distancia entre la mediana y la media está limitada por una desviación estándar . ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\bar {X}}}$

Este límite fue demostrado por Book y Sher en 1979 para muestras discretas, ^[13] y de manera más general por Page y Murty en 1982. ^[14] En un comentario sobre una prueba posterior de O'Cinneide, ^[15] Mallows en 1991 presentó una prueba compacta que utiliza la desigualdad de Jensen dos veces, ^[16] de la siguiente manera. Usando |·| para el valor absoluto , tenemos

${\displaystyle {\begin{aligned}|\mu -m|=|\operatorname {E} (X-m)|&\leq \operatorname {E} (|X-m|)\\&\leq \operatorname {E} (|X-\mu |)\\&\leq {\sqrt {\operatorname {E} \left((X-\mu )^{2}\right)}}=\sigma .\end{aligned}}}$

La primera y la tercera desigualdad provienen de la desigualdad de Jensen aplicada a la función de valor absoluto y a la función al cuadrado, que son ambas convexas. La segunda desigualdad proviene del hecho de que la mediana minimiza la función de desviación absoluta . ${\displaystyle a\mapsto \operatorname {E} (|X-a|)}$

La prueba de Mallows se puede generalizar para obtener una versión multivariada de la desigualdad ^[17] simplemente reemplazando el valor absoluto con una norma :

${\displaystyle \|\mu -m\|\leq {\sqrt {\operatorname {E} \left(\|X-\mu \|^{2}\right)}}={\sqrt {\operatorname {trace} \left(\operatorname {var} (X)\right)}}}$

donde m es una mediana espacial , es decir, un minimizador de la función La mediana espacial es única cuando la dimensión del conjunto de datos es dos o más. ^{[18] [19]} ${\displaystyle a\mapsto \operatorname {E} (\|X-a\|).\,}$

Una prueba alternativa utiliza la desigualdad unilateral de Chebyshev; aparece en una desigualdad sobre los parámetros de escala y ubicación . Esta fórmula también se deduce directamente de la desigualdad de Cantelli . ^[20]

Distribuciones unimodales

Para el caso de distribuciones unimodales , se puede lograr un límite más preciso en la distancia entre la mediana y la media:

${\displaystyle \left|{\tilde {X}}-{\bar {X}}\right|\leq \left({\frac {3}{5}}\right)^{\frac {1}{2}}\sigma \approx 0.7746\sigma }$. ^[21]

Una relación similar existe entre la mediana y la moda:

${\displaystyle \left|{\tilde {X}}-\mathrm {mode} \right|\leq 3^{\frac {1}{2}}\sigma \approx 1.732\sigma .}$

La media es mayor que la mediana para distribuciones monótonas.

Media, mediana y asimetría

Una heurística típica es que las distribuciones sesgadas positivamente tienen media > mediana. Esto es cierto para todos los miembros de la familia de distribuciones de Pearson . Sin embargo, esto no siempre es cierto. Por ejemplo, la familia de distribuciones de Weibull tiene miembros con media positiva, pero media < mediana. Las violaciones de la regla son particularmente comunes para distribuciones discretas. Por ejemplo, cualquier distribución de Poisson tiene sesgo positivo, pero su media < mediana siempre que . ^[22] Ver ^[23] para un esbozo de prueba. ${\displaystyle \mu {\bmod {1}}>\ln 2}$

Cuando la distribución tiene una densidad de probabilidad monótonamente decreciente, entonces la mediana es menor que la media, como se muestra en la figura.

Desigualdad de Jensen para medianas

La desigualdad de Jensen establece que para cualquier variable aleatoria X con una expectativa finita E [ X ] y para cualquier función convexa f

${\displaystyle f[E(x)]\leq E[f(x)]}$

Esta desigualdad se generaliza también a la mediana. Decimos que una función f : R → R es una función C si, para cualquier t ,

${\displaystyle f^{-1}\left(\,(-\infty ,t]\,\right)=\{x\in \mathbb {R} \mid f(x)\leq t\}}$

es un intervalo cerrado (permitiendo los casos degenerados de un único punto o un conjunto vacío ). Toda función convexa es una función C, pero lo inverso no se cumple. Si f es una función C, entonces

${\displaystyle f(\operatorname {med} [X])\leq \operatorname {med} [f(X)]}$

Si las medianas no son únicas, la afirmación es válida para la suprema correspondiente. ^[24]

Medianas para muestras

Cálculo eficiente de la mediana de la muestra

Aunque la ordenación por comparación de n elementos requiere Ω ( n log n ) operaciones, los algoritmos de selección pueden calcular el k -ésimo más pequeño de n elementos con solo Θ( n ) operaciones. Esto incluye la mediana, que es la ⁠norte/2estadística de orden n (o para un número par de muestras, la media aritmética de las dos estadísticas de orden medio). ^[25]

Los algoritmos de selección aún tienen la desventaja de requerir Ω( n ) de memoria, es decir, necesitan tener la muestra completa (o una porción de tamaño lineal de ella) en la memoria. Debido a que esto, así como el requisito de tiempo lineal, puede ser prohibitivo, se han desarrollado varios procedimientos de estimación para la mediana. Uno simple es la regla de la mediana de tres, que estima la mediana como la mediana de una submuestra de tres elementos; esto se usa comúnmente como una subrutina en el algoritmo de ordenamiento quicksort , que usa una estimación de la mediana de su entrada. Un estimador más robusto es el noveno de Tukey , que es la regla de la mediana de tres aplicada con recursión limitada: ^[26] si A es la muestra dispuesta como una matriz , y

med3( A ) = med( A [1], A [ ⁠norte/2⁠ ], A [ n ]) ,

entonces

noveno( A ) = med3(med3( A [1 ... ⁠1/3⁠ n ]), med3( A [ ⁠1/3⁠ n ... ⁠2/3⁠ n ]), med3( A [ ⁠2/3⁠ n ... n ]))

El remedian es un estimador de la mediana que requiere tiempo lineal pero memoria sublineal, operando en una sola pasada sobre la muestra. ^[27]

Distribución de muestreo

Las distribuciones tanto de la media de la muestra como de la mediana de la muestra se determinaron mediante Laplace . ^[28] La distribución de la mediana de la muestra de una población con una función de densidad es asintóticamente normal con media y varianza ^[29] ${\displaystyle f(x)}$ ${\displaystyle \mu }$

${\displaystyle {\frac {1}{4nf(m)^{2}}}}$

donde es la mediana de y es el tamaño de la muestra: ${\displaystyle m}$ ${\displaystyle f(x)}$ ${\displaystyle n}$

${\displaystyle {\text{Sample median}}\sim {\mathcal {N}}\left(\mu =m,\sigma ^{2}={\frac {1}{4nf(m)^{2}}}\right)}$

A continuación se presenta una demostración moderna. El resultado de Laplace se entiende ahora como un caso especial de la distribución asintótica de cuantiles arbitrarios .

Para muestras normales, la densidad es , por lo tanto, para muestras grandes la varianza de la mediana es igual a ^[7] (ver también la sección #Eficiencia a continuación). ${\displaystyle f(m)=1/{\sqrt {2\pi \sigma ^{2}}}}$ ${\displaystyle ({\pi }/{2})\cdot (\sigma ^{2}/n).}$

Derivación de la distribución asintótica

Suponemos que el tamaño de la muestra es un número impar y que nuestra variable es continua; la fórmula para el caso de variables discretas se proporciona a continuación en § Densidad local empírica. La muestra se puede resumir como "por debajo de la mediana", "en la mediana" y "por encima de la mediana", lo que corresponde a una distribución trinomial con probabilidades , y . Para una variable continua, la probabilidad de que varios valores de la muestra sean exactamente iguales a la mediana es 0, por lo que se puede calcular la densidad de en el punto directamente a partir de la distribución trinomial: ${\displaystyle N=2n+1}$ ${\displaystyle F(v)}$ ${\displaystyle f(v)}$ ${\displaystyle 1-F(v)}$ ${\displaystyle v}$

${\displaystyle \Pr[\operatorname {med} =v]\,dv={\frac {(2n+1)!}{n!n!}}F(v)^{n}(1-F(v))^{n}f(v)\,dv}$.

Ahora presentamos la función beta. Para argumentos enteros y , esto se puede expresar como . Además, recuerde que . El uso de estas relaciones y la configuración de y iguales a permite que la última expresión se escriba como ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \mathrm {B} (\alpha ,\beta )={\frac {(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}}}$ ${\displaystyle f(v)\,dv=dF(v)}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle n+1}$

${\displaystyle {\frac {F(v)^{n}(1-F(v))^{n}}{\mathrm {B} (n+1,n+1)}}\,dF(v)}$

Por lo tanto, la función de densidad de la mediana es una distribución beta simétrica impulsada hacia adelante por . Su media, como esperaríamos, es 0,5 y su varianza es . Por la regla de la cadena , la varianza correspondiente de la mediana de la muestra es ${\displaystyle F}$ ${\displaystyle 1/(4(N+2))}$

${\displaystyle {\frac {1}{4(N+2)f(m)^{2}}}}$.

El 2 adicional es despreciable en el límite .

Densidad local empírica

En la práctica, las funciones y anteriores no suelen conocerse ni suponerse. Sin embargo, se pueden estimar a partir de una distribución de frecuencias observada. En esta sección, ofrecemos un ejemplo. Considere la siguiente tabla, que representa una muestra de 3800 observaciones (de valor discreto): ${\displaystyle f}$ ${\displaystyle F}$

Como las observaciones tienen valores discretos, construir la distribución exacta de la mediana no es una traducción inmediata de la expresión anterior para ; uno puede (y normalmente lo hace) tener múltiples instancias de la mediana en su muestra. Por lo tanto, debemos sumar todas estas posibilidades: ${\displaystyle \Pr(\operatorname {med} =v)}$

${\displaystyle \Pr(\operatorname {med} =v)=\sum _{i=0}^{n}\sum _{k=0}^{n}{\frac {N!}{i!(N-i-k)!k!}}F(v-1)^{i}(1-F(v))^{k}f(v)^{N-i-k}}$

Aquí, i es el número de puntos estrictamente menores que la mediana y k el número estrictamente mayor.

Con estos datos preliminares, es posible investigar el efecto del tamaño de la muestra sobre los errores estándar de la media y la mediana. La media observada es 3,16, la mediana bruta observada es 3 y la mediana interpolada observada es 3,174. La siguiente tabla ofrece algunas estadísticas de comparación.

El valor esperado de la mediana disminuye ligeramente a medida que aumenta el tamaño de la muestra, mientras que, como cabría esperar, los errores estándar tanto de la mediana como de la media son proporcionales a la raíz cuadrada inversa del tamaño de la muestra. La aproximación asintótica es demasiado cautelosa al sobreestimar el error estándar.

Estimación de la varianza a partir de datos de muestra

Varios autores han estudiado el valor de —el valor asintótico de donde es la mediana de la población—. El método estándar de " eliminar uno" produce resultados inconsistentes . ^[30] Se ha demostrado que una alternativa —el método de "eliminar k"— donde crece con el tamaño de la muestra es asintóticamente consistente. ^[31] Este método puede ser computacionalmente costoso para grandes conjuntos de datos. Se sabe que una estimación bootstrap es consistente, ^[32] pero converge muy lentamente ( orden de ). ^[33] Se han propuesto otros métodos pero su comportamiento puede diferir entre muestras grandes y pequeñas. ^[34] ${\displaystyle (2f(x))^{-2}}$ ${\displaystyle n^{-1/2}(\nu -m)}$ ${\displaystyle \nu }$ ${\displaystyle k}$ ${\displaystyle n^{-{\frac {1}{4}}}}$

Eficiencia

La eficiencia de la mediana de la muestra, medida como la relación entre la varianza de la media y la varianza de la mediana, depende del tamaño de la muestra y de la distribución de la población subyacente. Para una muestra de tamaño de distribución normal , la eficiencia para un N grande es ${\displaystyle N=2n+1}$

${\displaystyle {\frac {2}{\pi }}{\frac {N+2}{N}}}$

La eficiencia tiende a medida que tiende a infinito. ${\displaystyle {\frac {2}{\pi }}}$ ${\displaystyle N}$

En otras palabras, la varianza relativa de la mediana será , o 57% mayor que la varianza de la media – el error estándar relativo de la mediana será , o 25% mayor que el error estándar de la media , (ver también la sección #Distribución de muestreo arriba). ^[35] ${\displaystyle \pi /2\approx 1.57}$ ${\displaystyle (\pi /2)^{\frac {1}{2}}\approx 1.25}$ ${\displaystyle \sigma /{\sqrt {n}}}$

Otros estimadores

Para distribuciones univariadas que son simétricas respecto de una mediana, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la mediana de la población. ^[36]

Si los datos se representan mediante un modelo estadístico que especifica una familia particular de distribuciones de probabilidad , entonces se pueden obtener estimaciones de la mediana ajustando esa familia de distribuciones de probabilidad a los datos y calculando la mediana teórica de la distribución ajustada. La interpolación de Pareto es una aplicación de esto cuando se supone que la población tiene una distribución de Pareto .

Mediana multivariada

Anteriormente, en este artículo se habló de la mediana univariante, cuando la muestra o población tenía una dimensión. Cuando la dimensión es dos o más, hay múltiples conceptos que amplían la definición de la mediana univariante; cada una de esas medianas multivariantes concuerda con la mediana univariante cuando la dimensión es exactamente una. ^{[36] [37] [38] [39]}

Mediana marginal

La mediana marginal se define para vectores definidos con respecto a un conjunto fijo de coordenadas. Una mediana marginal se define como el vector cuyos componentes son medianas univariadas. La mediana marginal es fácil de calcular y sus propiedades fueron estudiadas por Puri y Sen. ^{[36] [40]}

Mediana geométrica

La mediana geométrica de un conjunto discreto de puntos de muestra en un espacio euclidiano es el punto ^[a] que minimiza la suma de las distancias a los puntos de muestra. ${\displaystyle x_{1},\ldots x_{N}}$

${\displaystyle {\hat {\mu }}={\underset {\mu \in \mathbb {R} ^{m}}{\operatorname {arg\,min} }}\sum _{n=1}^{N}\left\|\mu -x_{n}\right\|_{2}}$

A diferencia de la mediana marginal, la mediana geométrica es equivariante con respecto a las transformaciones de similitud euclidiana, como las traslaciones y las rotaciones .

Mediana en todas las direcciones

Si las medianas marginales de todos los sistemas de coordenadas coinciden, entonces su ubicación común puede denominarse "mediana en todas las direcciones". ^[42] Este concepto es relevante para la teoría de la votación debido al teorema del votante mediano . Cuando existe, la mediana en todas las direcciones coincide con la mediana geométrica (al menos para distribuciones discretas).

Punto central

En estadística y geometría computacional , la noción de punto central es una generalización de la mediana a los datos en el espacio euclidiano de dimensiones superiores . Dado un conjunto de puntos en el espacio d -dimensional, un punto central del conjunto es un punto tal que cualquier hiperplano que pase por ese punto divide el conjunto de puntos en dos subconjuntos aproximadamente iguales: la parte más pequeña debe tener al menos una fracción de 1/( d  + 1) de los puntos. Al igual que la mediana, un punto central no necesita ser uno de los puntos de datos. Cada conjunto de puntos no vacío (sin duplicados) tiene al menos un punto central.

Mediana condicional

La mediana condicional se da en el contexto en el que buscamos estimar una variable aleatoria a partir de una variable aleatoria , que es una versión ruidosa de . La mediana condicional en este contexto está dada por ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$

${\displaystyle m(X|Y=y)=F_{X|Y=y}^{-1}\left({\frac {1}{2}}\right)}$

donde es la inversa de la función de distribución acumulativa condicional (es decir, la función cuantil condicional) de . Por ejemplo, un modelo popular es donde es la normal estándar independiente de . La mediana condicional es el estimador bayesiano óptimo: ${\displaystyle t\mapsto F_{X|Y=y}^{-1}(t)}$ ${\displaystyle x\mapsto F_{X|Y}(x|y)}$ ${\displaystyle Y=X+Z}$ ${\displaystyle Z}$ ${\displaystyle X}$ ${\displaystyle L_{1}}$

${\displaystyle m(X|Y=y)=\arg \min _{f}\mathbb {E} \left[|X-f(Y)|\right]}$

Se sabe que para el modelo donde es normal estándar independiente de , el estimador es lineal si y sólo si es gaussiano. ^[43] ${\displaystyle Y=X+Z}$ ${\displaystyle Z}$ ${\displaystyle X}$ ${\displaystyle X}$

Otros conceptos relacionados con la mediana

Mediana interpolada

Cuando se trabaja con una variable discreta, a veces es útil considerar los valores observados como puntos medios de intervalos continuos subyacentes. Un ejemplo de esto es una escala de Likert , en la que se expresan opiniones o preferencias en una escala con un número determinado de respuestas posibles. Si la escala consta de números enteros positivos, una observación de 3 podría considerarse como la representación del intervalo de 2,50 a 3,50. Es posible estimar la mediana de la variable subyacente. Si, por ejemplo, el 22% de las observaciones tienen un valor de 2 o inferior y el 55,0% tienen un valor de 3 o inferior (por lo que el 33% tiene el valor 3), entonces la mediana es 3, ya que la mediana es el valor más pequeño de para el cual es mayor que la mitad. Pero la mediana interpolada está en algún lugar entre 2,50 y 3,50. Primero sumamos la mitad del ancho del intervalo a la mediana para obtener el límite superior del intervalo de la mediana. Luego restamos esa proporción del ancho del intervalo que es igual a la proporción del 33% que se encuentra por encima de la marca del 50%. En otras palabras, dividimos el ancho del intervalo en proporción a la cantidad de observaciones. En este caso, el 33% se divide en un 28% por debajo de la mediana y un 5% por encima de ella, por lo que restamos 5/33 del ancho del intervalo del límite superior de 3,50 para obtener una mediana interpolada de 3,35. Más formalmente, si se conocen los valores, la mediana interpolada se puede calcular a partir de ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle F(x)}$ ${\displaystyle w}$ ${\displaystyle f(x)}$

${\displaystyle m_{\text{int}}=m+w\left[{\frac {1}{2}}-{\frac {F(m)-{\frac {1}{2}}}{f(m)}}\right].}$

Alternativamente, si en una muestra observada hay puntuaciones por encima de la categoría mediana, puntuaciones en ella y puntuaciones por debajo de ella, entonces la mediana interpolada se da por ${\displaystyle k}$ ${\displaystyle j}$ ${\displaystyle i}$

${\displaystyle m_{\text{int}}=m+{\frac {w}{2}}\left[{\frac {k-i}{j}}\right].}$

Pseudo-mediana

Para distribuciones univariadas que son simétricas respecto de una mediana, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la mediana poblacional; para distribuciones no simétricas, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la pseudomediana poblacional , que es la mediana de una distribución simetrizada y que está cerca de la mediana poblacional. ^[44] El estimador de Hodges-Lehmann se ha generalizado a distribuciones multivariadas. ^[45]

Variantes de regresión

El estimador de Theil-Sen es un método de regresión lineal robusta basado en la búsqueda de medianas de pendientes . ^[46]

Filtro de mediana

El filtro mediano es una herramienta importante de procesamiento de imágenes , que puede eliminar eficazmente cualquier ruido de sal y pimienta de las imágenes en escala de grises .

Análisis de conglomerados

En el análisis de conglomerados , el algoritmo de agrupamiento de k-medianas proporciona una forma de definir conglomerados, en la que el criterio de maximizar la distancia entre las medias de los conglomerados que se utiliza en el agrupamiento de k-medias se reemplaza por la maximización de la distancia entre las medianas de los conglomerados.

Línea mediana-mediana

Este es un método de regresión robusta. La idea se remonta a Wald en 1940, quien sugirió dividir un conjunto de datos bivariados en dos mitades dependiendo del valor del parámetro independiente : una mitad izquierda con valores menores que la mediana y una mitad derecha con valores mayores que la mediana. ^[47] Sugirió tomar las medias de las variables dependientes e independientes de las mitades izquierda y derecha y estimar la pendiente de la línea que une estos dos puntos. La línea podría luego ajustarse para adaptarse a la mayoría de los puntos en el conjunto de datos. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$

En 1942, Nair y Shrivastava sugirieron una idea similar, pero en su lugar propusieron dividir la muestra en tres partes iguales antes de calcular las medias de las submuestras. ^[48] En 1951, Brown y Mood propusieron la idea de utilizar las medianas de dos submuestras en lugar de las medias. ^[49] Tukey combinó estas ideas y recomendó dividir la muestra en tres submuestras de igual tamaño y estimar la línea basándose en las medianas de las submuestras. ^[50]

Estimadores medianamente imparciales

Cualquier estimador insesgado a la media minimiza el riesgo ( pérdida esperada ) con respecto a la función de pérdida por error al cuadrado , como observó Gauss . Un estimador insesgado a la mediana minimiza el riesgo con respecto a la función de pérdida por desviación absoluta , como observó Laplace . Otras funciones de pérdida se utilizan en la teoría estadística , particularmente en la estadística robusta .

La teoría de los estimadores medianamente imparciales fue revivida por George W. Brown en 1947: ^[51]

Se dirá que una estimación de un parámetro unidimensional θ es insesgada respecto de la mediana si, para un valor θ fijo, la mediana de la distribución de la estimación se encuentra en el valor θ; es decir, la estimación subestima con la misma frecuencia con la que sobreestima. Este requisito parece cumplir, para la mayoría de los propósitos, tanto como el requisito de insesgada respecto de la media y tiene la propiedad adicional de que es invariante ante una transformación uno a uno.

—  página 584

Se han informado otras propiedades de los estimadores medianamente imparciales. ^{[52] [53] [54] [55]}

Existen métodos para construir estimadores insesgados a la mediana que son óptimos (en un sentido análogo a la propiedad de varianza mínima para estimadores insesgados a la media). Tales construcciones existen para distribuciones de probabilidad que tienen funciones de verosimilitud monótonas . ^{[56] [57]} Uno de estos procedimientos es un análogo del procedimiento de Rao-Blackwell para estimadores insesgados a la media: el procedimiento se aplica a una clase más pequeña de distribuciones de probabilidad que el procedimiento de Rao-Blackwell, pero a una clase más grande de funciones de pérdida . ^[58]

Historia

Parece que los investigadores científicos del antiguo Oriente Próximo no utilizaron estadísticas resumidas en su totalidad, sino que eligieron valores que ofrecían la máxima coherencia con una teoría más amplia que integraba una amplia variedad de fenómenos. ^[59] En la comunidad académica mediterránea (y, más tarde, europea), las estadísticas como la media son fundamentalmente un desarrollo medieval y moderno temprano. (La historia de la mediana fuera de Europa y sus predecesoras sigue siendo relativamente poco estudiada.)

La idea de la mediana apareció en el siglo VI en el Talmud , con el fin de analizar de manera justa las valoraciones divergentes . ^{[60] [61]} Sin embargo, el concepto no se extendió a la comunidad científica más amplia.

En cambio, el antepasado más cercano de la mediana moderna es el rango medio , inventado por Al-Biruni ^{[62] : 31  [63]} La transmisión de su trabajo a los eruditos posteriores no está clara. Aplicó su técnica para ensayar metales monetarios, pero, después de publicar su trabajo, la mayoría de los ensayadores todavía adoptaban el valor más desfavorable de sus resultados, para que no parecieran hacer trampa . ^{[62] : 35–8  [64]} Sin embargo, el aumento de la navegación en el mar durante la Era de los Descubrimientos significó que los navegantes de los barcos tenían que intentar cada vez más determinar la latitud en condiciones meteorológicas desfavorables contra costas hostiles, lo que llevó a un renovado interés en las estadísticas resumidas. Ya sea redescubierto o inventado independientemente, el rango medio se recomienda a los navegantes náuticos en "Instrucciones para el viaje de Raleigh a Guayana, 1595" de Harriot. ^{[62] : 45–8}

La idea de la mediana puede haber aparecido por primera vez en el libro de Edward Wright de 1599 Certaine Errors in Navigation en una sección sobre navegación con brújula . ^[65] Wright era reacio a descartar valores medidos, y puede haber sentido que la mediana, que incorpora una mayor proporción del conjunto de datos que el rango medio , tenía más probabilidades de ser correcta. Sin embargo, Wright no dio ejemplos del uso de su técnica, lo que dificulta verificar que describiera la noción moderna de mediana. ^{[59] [63] [b]} La mediana (en el contexto de la probabilidad) ciertamente apareció en la correspondencia de Christiaan Huygens , pero como un ejemplo de una estadística que era inapropiada para la práctica actuarial . ^[59]

La primera recomendación de la mediana data de 1757, cuando Roger Joseph Boscovich desarrolló un método de regresión basado en la norma L 1 y, por lo tanto, implícitamente en la mediana. ^{[59] [66]} En 1774, Laplace hizo explícito este deseo: sugirió que la mediana se utilizara como el estimador estándar del valor de una PDF posterior . El criterio específico era minimizar la magnitud esperada del error; donde es la estimación y es el valor verdadero. Con este fin, Laplace determinó las distribuciones tanto de la media de la muestra como de la mediana de la muestra a principios del siglo XIX. ^{[28] [67]} Sin embargo, una década después, Gauss y Legendre desarrollaron el método de mínimos cuadrados , que minimiza para obtener la media; la fuerte justificación de este estimador por referencia a la estimación de máxima verosimilitud basada en una distribución normal significa que ha reemplazado en gran medida la sugerencia original de Laplace. ^[68] ${\displaystyle |\alpha -\alpha ^{*}|}$ ${\displaystyle \alpha ^{*}}$ ${\displaystyle \alpha }$ ${\displaystyle (\alpha -\alpha ^{*})^{2}}$

Antoine Augustin Cournot en 1843 fue el primero ^[69] en utilizar el término mediana ( valeur médiane ) para el valor que divide una distribución de probabilidad en dos mitades iguales. Gustav Theodor Fechner utilizó la mediana ( Centralwerth ) en fenómenos sociológicos y psicológicos. ^[70] Anteriormente se había utilizado solo en astronomía y campos relacionados. Gustav Fechner popularizó la mediana en el análisis formal de datos, aunque había sido utilizada previamente por Laplace, ^[70] y la mediana apareció en un libro de texto de FY Edgeworth . ^[71] Francis Galton utilizó el término mediana en 1881, ^{[72] [73]} habiendo utilizado anteriormente los términos valor más intermedio en 1869, y medio en 1880. ^{[74] [75]}

Véase también

• Portal de matemáticas

• Desviación absoluta  : diferencia entre el valor observado de una variable y un valor de referenciaPages displaying short descriptions of redirect targets
• Sesgo de un estimador  – Propiedad estadística
• Tendencia central  : Valor estadístico que representa el centro o el promedio de una distribución.
• Concentración de medida  – Parámetro estadístico de las funciones de Lipschitz  – Forma fuerte de continuidad uniformePages displaying short descriptions of redirect targets
• Gráfica mediana  : Gráfica con una mediana para cada tres vértices
• Mediana de medianas  – Algoritmo rápido de mediana aproximada – Algoritmo para calcular la mediana aproximada en tiempo lineal
• Búsqueda de mediana  : método para encontrar el k-ésimo valor más pequeñoPages displaying short descriptions of redirect targets
• Pendiente mediana  : método estadístico para ajustar una líneaPages displaying short descriptions of redirect targets
• Teoría del votante mediano  : teorema en ciencia políticaPages displaying short descriptions of redirect targets
• Medoid  – objetos representativos de un conjunto de datos o un grupo dentro de un conjunto de datos cuya suma de diferencias con todos los objetos del grupo es mínima Pages displaying wikidata descriptions as a fallbacks – Generalización de la mediana en dimensiones superiores
• Media móvil#Mediana móvil  – Tipo de medida estadística sobre subconjuntos de un conjunto de datos
• Desviación absoluta media  : medida estadística de variabilidad

Notas

1. La mediana geométrica es única a menos que la muestra sea colineal. ^[41]
2. Los estudiosos posteriores parecen coincidir con Eisenhart en que las cifras de Boroughs de 1580, aunque sugieren la mediana, de hecho describen una media aritmética.; ^{[62] : 62–3} Boroughs no es mencionado en ningún otro trabajo.

Referencias

1. Weisstein, Eric W. "Mediana estadística". MathWorld .
2. Simon, Laura J.; "Estadísticas descriptivas" Archivado el 30 de julio de 2010 en Wayback Machine , Kit de recursos de educación estadística , Departamento de Estadística del Estado de Pensilvania
3. Derek Bissell (1994). Métodos estadísticos para Spc y Tqm. CRC Press. pp. 26–. ISBN 978-0-412-39440-9. Recuperado el 25 de febrero de 2013 .
4. David J. Sheskin (27 de agosto de 2003). Manual de procedimientos estadísticos paramétricos y no paramétricos (tercera edición). CRC Press. pág. 7. ISBN 978-1-4200-3626-8. Recuperado el 25 de febrero de 2013 .
5. Paul T. von Hippel (2005). "Media, mediana y asimetría: corrección de una regla de libro de texto". Journal of Statistics Education . 13 (2). Archivado desde el original el 14 de octubre de 2008 . Consultado el 18 de junio de 2015 .
6. Robson, Colin (1994). Experimento, diseño y estadística en psicología . Penguin. Págs. 42-45. ISBN. 0-14-017648-9.
7. Williams, D. (2001). Weighing the Odds (Pesando las probabilidades) . Cambridge University Press. pág. 165. ISBN 052100618X.
8. Maindonald, John; Braun, W. John (6 de mayo de 2010). Análisis de datos y gráficos con R: un enfoque basado en ejemplos. Cambridge University Press. pág. 104. ISBN 978-1-139-48667-5.
9. "AP Statistics Review - Curvas de densidad y distribuciones normales". Archivado desde el original el 8 de abril de 2015 . Consultado el 16 de marzo de 2015 .
10. Newman, MEJ (2005). "Leyes de potencia, distribuciones de Pareto y ley de Zipf". Contemporary Physics . 46 (5): 323–351. arXiv : cond-mat/0412004 . Código Bibliográfico :2005ConPh..46..323N. doi :10.1080/00107510500052444. S2CID  2871747.
11. Stroock, Daniel (2011). Probability Theory . Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3.
12. DeGroot, Morris H. (1970). Decisiones estadísticas óptimas. McGraw-Hill Book Co., Nueva York-Londres-Sydney. pág. 232. ISBN 9780471680291.Sr. 0356303  .
13. Stephen A. Book; Lawrence Sher (1979). "¿Qué tan cerca están la media y la mediana?". The Two-Year College Mathematics Journal . 10 (3): 202–204. doi :10.2307/3026748. JSTOR  3026748 . Consultado el 12 de marzo de 2022 .
14. Warren Page; Vedula N. Murty (1982). "Relaciones de proximidad entre medidas de tendencia central y dispersión: Parte 1". The Two-Year College Mathematics Journal . 13 (5): 315–327. doi :10.1080/00494925.1982.11972639 (inactivo el 1 de noviembre de 2024) . Consultado el 12 de marzo de 2022 .{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
15. O'Cinneide, Colm Art (1990). "La media está dentro de una desviación estándar de cualquier mediana". The American Statistician . 44 (4): 292–293. doi :10.1080/00031305.1990.10475743 . Consultado el 12 de marzo de 2022 .
16. Mallows, Colin (agosto de 1991). "Otro comentario sobre O'Cinneide". The American Statistician . 45 (3): 257. doi :10.1080/00031305.1991.10475815.
17. Piché, Robert (2012). Vectores aleatorios y secuencias aleatorias . Lambert Academic Publishing. ISBN 978-3659211966.
18. Kemperman, Johannes HB (1987). Dodge, Yadolah (ed.). "La mediana de una medida finita en un espacio de Banach: análisis estadístico de datos basado en la norma L1 y métodos relacionados". Documentos de la Primera Conferencia Internacional celebrada en Neuchâtel, del 31 de agosto al 4 de septiembre de 1987. Ámsterdam: North-Holland Publishing Co.: 217–230. MR  0949228.
19. Milasevic, Philip; Ducharme, Gilles R. (1987). "Singularidad de la mediana espacial". Anales de Estadística . 15 (3): 1332–1333. doi : 10.1214/aos/1176350511 . MR  0902264.
20. K. Van Steen Notas sobre probabilidad y estadística
21. Basu, S.; Dasgupta, A. (1997). "La media, la mediana y la moda de distribuciones unimodales: una caracterización". Teoría de la probabilidad y sus aplicaciones . 41 (2): 210–223. doi :10.1137/S0040585X97975447. S2CID  54593178.
22. von Hippel, Paul T. (enero de 2005). "Media, mediana y asimetría: corrección de una regla de libro de texto". Revista de educación estadística . 13 (2). doi : 10.1080/10691898.2005.11910556 . ISSN  1069-1898.
23. Groeneveld, Richard A.; Meeden, Glen (agosto de 1977). "La desigualdad de la moda, la mediana y la media". The American Statistician . 31 (3): 120–121. doi :10.1080/00031305.1977.10479215. ISSN  0003-1305.
24. Merkle, M. (2005). "Desigualdad de Jensen para medianas". Statistics & Probability Letters . 71 (3): 277–281. doi :10.1016/j.spl.2004.11.010.
25. Alfred V. Aho y John E. Hopcroft y Jeffrey D. Ullman (1974). El diseño y análisis de algoritmos informáticos . Reading/MA: Addison-Wesley. ISBN 0-201-00029-6.Aquí: Sección 3.6 "Estadísticas de órdenes", p.97-99, en particular Algoritmo 3.6 y Teorema 3.9.
26. Bentley, Jon L.; McIlroy, M. Douglas (1993). "Ingeniería de una función de ordenación". Software: práctica y experiencia . 23 (11): 1249–1265. doi :10.1002/spe.4380231105. S2CID  8822797.
27. Rousseeuw, Peter J.; Bassett, Gilbert W. Jr. (1990). "El remediador: un método de promediado robusto para grandes conjuntos de datos" (PDF) . J. Amer. Statist. Assoc . 85 (409): 97–104. doi :10.1080/01621459.1990.10475311.
28. Stigler, Stephen (diciembre de 1973). "Estudios en la historia de la probabilidad y la estadística. XXXII: Laplace, Fisher y el descubrimiento del concepto de suficiencia". Biometrika . 60 (3): 439–445. doi :10.1093/biomet/60.3.439. JSTOR  2334992. MR  0326872.
29. Rider, Paul R. (1960). "Varianza de la mediana de muestras pequeñas de varias poblaciones especiales". J. Amer. Statist. Assoc. 55 (289): 148–150. doi :10.1080/01621459.1960.10482056.
30. Efron, B. (1982). El Jackknife, el Bootstrap y otros planes de remuestreo . Filadelfia: SIAM. ISBN 0898711797.
31. Shao, J.; Wu, CF (1989). "Una teoría general para la estimación de la varianza con el método Jackknife". Ann. Stat. 17 (3): 1176–1197. doi : 10.1214/aos/1176347263 . JSTOR  2241717.
32. Efron, B. (1979). "Métodos Bootstrap: otra mirada al método Jackknife". Ann. Stat. 7 (1): 1–26. doi : 10.1214/aos/1176344552 . JSTOR  2958830.
33. Hall, P.; Martin, MA (1988). "Tasa de convergencia exacta del estimador de varianza cuantil bootstrap". Campos relacionados con la teoría probabilística . 80 (2): 261–268. doi : 10.1007/BF00356105 . S2CID  119701556.
34. Jiménez-Gamero, MD; Muñoz-García, J.; Pino-Mejías, R. (2004). "Bootstrap reducido para la mediana". Estadística Sínica . 14 (4): 1179-1198.
35. Maindonald, John; John Braun, W. (6 de mayo de 2010). Análisis de datos y gráficos con R: un enfoque basado en ejemplos. Cambridge University Press. ISBN 9781139486675.
36. Hettmansperger, Thomas P.; McKean, Joseph W. (1998). Métodos estadísticos no paramétricos robustos . Biblioteca de Estadística de Kendall. Vol. 5. Londres: Edward Arnold. ISBN 0-340-54937-8.Sr. 1604954  .
37. Small, Christopher G. "Un estudio de medianas multidimensionales". Revista Internacional de Estadística (1990): 263-277. doi :10.2307/1403809 JSTOR  1403809
38. Niinimaa, A. y H. Oja. "Mediana multivariada". Enciclopedia de ciencias estadísticas (1999).
39. Mosler, Karl. Dispersión multivariante, regiones centrales y profundidad: el enfoque de la zona de sustentación. Vol. 165. Springer Science & Business Media, 2012.
40. Puri, Madan L.; Sen, Pranab K.; Métodos no paramétricos en análisis multivariante , John Wiley & Sons, Nueva York, NY, 1971. (Reimpreso por Krieger Publishing)
41. Vardi, Yehuda; Zhang, Cun-Hui (2000). "La mediana L1 multivariante y la profundidad de los datos asociados". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 97 (4): 1423–1426 (electrónico). Bibcode :2000PNAS...97.1423V. doi : 10.1073/pnas.97.4.1423 . MR  1740461. PMC 26449 . PMID  10677477. 
42. Davis, Otto A.; DeGroot, Morris H.; Hinich, Melvin J. (enero de 1972). "Ordenamientos de preferencias sociales y regla de la mayoría" (PDF) . Econometrica . 40 (1): 147–157. doi :10.2307/1909727. JSTOR  1909727.Los autores, trabajando en un tema en el que se supone la unicidad, utilizan de hecho la expresión " mediana única en todas las direcciones".
43. Barnes, Leighton; Dytso, Alex J.; Jingbo, Liu; Poor, H. Vincent (22 de agosto de 2024). "Estimación L1: sobre la optimalidad de los estimadores lineales". IEEE Transactions on Information Theory . 70 (11): 8026–8039. doi :10.1109/TIT.2024.3440929.
44. Pratt, William K.; Cooper, Ted J.; Kabir, Ihtisham (11 de julio de 1985). Corbett, Francis J (ed.). "Filtro pseudomediano". Arquitecturas y algoritmos para el procesamiento de imágenes digitales II . 0534 : 34. Bibcode :1985SPIE..534...34P. doi :10.1117/12.946562. S2CID  173183609.
45. Oja, Hannu (2010). Métodos no paramétricos multivariados con  R : un enfoque basado en signos y rangos espaciales . Lecture Notes in Statistics. Vol. 199. Nueva York, NY: Springer. pp. xiv+232. doi :10.1007/978-1-4419-0468-3. ISBN. 978-1-4419-0467-6.Señor 2598854  .
46. Wilcox, Rand R. (2001), "Estimador de Theil–Sen", Fundamentos de los métodos estadísticos modernos: mejora sustancial de la potencia y la precisión, Springer-Verlag, págs. 207-210, ISBN 978-0-387-95157-7.
47. Wald, A. (1940). "El ajuste de líneas rectas si ambas variables están sujetas a error" (PDF) . Anales de estadística matemática . 11 (3): 282–300. doi : 10.1214/aoms/1177731868 . JSTOR  2235677.
48. Nair, KR; Shrivastava, MP (1942). "Sobre un método simple de ajuste de curvas". Sankhyā: The Indian Journal of Statistics . 6 (2): 121–132. JSTOR  25047749.
49. Brown, GW; Mood, AM (1951). "Sobre las pruebas de mediana para hipótesis lineales". Actas del Segundo Simposio de Berkeley sobre Estadística Matemática y Probabilidad . Berkeley, CA: University of California Press. págs. 159–166. Zbl  0045.08606.
50. Tukey, JW (1977). Análisis exploratorio de datos. Reading, MA: Addison-Wesley. ISBN 0201076160.
51. Brown, George W. (1947). "Sobre la estimación de muestras pequeñas". Anales de estadística matemática . 18 (4): 582–585. doi : 10.1214/aoms/1177730349 . JSTOR  2236236.
52. Lehmann, Erich L. (1951). "Un concepto general de imparcialidad". Anales de estadística matemática . 22 (4): 587–592. doi : 10.1214/aoms/1177729549 . JSTOR  2236928.
53. Birnbaum, Allan (1961). "Una teoría unificada de la estimación, I". Anales de estadística matemática . 32 (1): 112–135. doi : 10.1214/aoms/1177705145 . JSTOR  2237612.
54. van der Vaart, H. Robert (1961). "Algunas extensiones de la idea de sesgo". Anales de estadística matemática . 32 (2): 436–447. doi : 10.1214/aoms/1177705051 . JSTOR  2237754. MR  0125674.
55. Pfanzagl, Johann; con la ayuda de R. Hamböker (1994). Teoría estadística paramétrica . Walter de Gruyter. ISBN 3-11-013863-8.Señor 1291393  .
56. Pfanzagl, Johann. "Sobre estimadores óptimos de mediana no sesgados en presencia de parámetros molestos". Anales de estadística (1979): 187-193.
57. Brown, LD; Cohen, Arthur; Strawderman, WE (1976). "Un teorema de clase completo para la razón de verosimilitud monótona estricta con aplicaciones". Ann. Statist . 4 (4): 712–722. doi : 10.1214/aos/1176343543 .
58. Página; Brown, LD; Cohen, Arthur; Strawderman, WE (1976). "Un teorema de clase completo para la razón de verosimilitud estrictamente monótona con aplicaciones". Ann. Statist . 4 (4): 712–722. doi : 10.1214/aos/1176343543 .
59. Bakker, Arthur; Gravemeijer, Koeno PE (1 de junio de 2006). "Una fenomenología histórica de la media y la mediana". Estudios Educativos en Matemáticas . 62 (2): 149-168. doi :10.1007/s10649-006-7099-8. ISSN  1573-0816. S2CID  143708116.
60. Adler, Dan (31 de diciembre de 2014). "Talmud y economía moderna". Asuntos judíos estadounidenses e israelíes . Archivado desde el original el 6 de diciembre de 2015. Consultado el 22 de febrero de 2020 .
61. Teoría económica moderna en el Talmud de Yisrael Aumann
62. Eisenhart, Churchill (24 de agosto de 1971). El desarrollo del concepto de la mejor media de un conjunto de mediciones desde la antigüedad hasta la actualidad (PDF) (Discurso). 131.ª Reunión Anual de la Asociación Estadounidense de Estadística. Universidad Estatal de Colorado.
63. "Cómo el promedio triunfó sobre la mediana". Priceonomics . 5 de abril de 2016 . Consultado el 23 de febrero de 2020 .
64. Sangster, Alan (marzo de 2021). "La vida y obra de Luca Pacioli (1446/7–1517), educador humanista". Abacus . 57 (1): 126–152. doi :10.1111/abac.12218. hdl : 2164/16100 . ISSN  0001-3072. S2CID  233917744.
65. Wright, Edward; Parsons, EJS; Morris, WF (1939). "Edward Wright y su obra". Imago Mundi . 3 : 61–71. doi :10.1080/03085693908591862. ISSN  0308-5694. JSTOR  1149920.
66. Stigler, SM (1986). Historia de la estadística: la medición de la incertidumbre antes de 1900. Harvard University Press. ISBN 0674403401.
67. Laplace PS de (1818) Deuxième supplément à la Théorie Analytique des Probabilités , París, Courcier
68. Jaynes, ET (2007). Teoría de la probabilidad: la lógica de la ciencia (5.ª edición impresa). Cambridge [ua]: Cambridge Univ. Press. p. 172. ISBN 978-0-521-59271-0.
69. Howarth, Richard (2017). Diccionario de geociencias matemáticas: con notas históricas . Springer. pág. 374.
70. Keynes, JM (1921) Tratado sobre probabilidad . Parte II, capítulo XVII, apartado 5 (p. 201) (reimpresión de 2006, Cosimo Classics, ISBN 9781596055308  : varias otras reimpresiones) 
71. Stigler, Stephen M. (2002). Estadísticas sobre la mesa: la historia de los conceptos y métodos estadísticos. Harvard University Press. pp. 105–7. ISBN 978-0-674-00979-0.
72. Galton F (1881) "Informe del Comité Antropométrico", págs. 245-260. Informe de la 51.ª reunión de la Asociación Británica para el Avance de la Ciencia
73. David, HA (1995). "Primera (?) aparición de términos comunes en estadística matemática". The American Statistician . 49 (2): 121–133. doi :10.2307/2684625. ISSN  0003-1305. JSTOR  2684625.
74. enciclopediaofmath.org
75. personal.psu.edu

Enlaces externos

• "Mediana (en estadística)", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Mediana como media aritmética ponderada de todas las observaciones de la muestra
• Calculadora en línea
• Calcular la mediana
• Un problema que involucra la media, la mediana y la moda.
• Weisstein, Eric W. "Mediana estadística". MathWorld .
• Script de Python para cálculos de mediana y métricas de desigualdad de ingresos
• Cálculo rápido de la mediana mediante binning sucesivo
• 'Media, mediana, moda y asimetría', un tutorial diseñado para estudiantes de psicología de primer año en la Universidad de Oxford, basado en un ejemplo práctico.
• El complejo problema matemático del SAT que incluso el College Board resolvió mal: Andrew Daniels en Popular Mechanics

Este artículo incorpora material de Median de una distribución en PlanetMath , que está licenciada bajo la Licencia Creative Commons Atribución/Compartir-Igual .