En ciencias políticas y teoría de la elección social , el teorema del votante mediano establece que si los votantes y los candidatos se distribuyen a lo largo de un espectro unidimensional y los votantes tienen preferencias máximas únicas , cualquier método de votación que satisfaga el criterio de Condorcet elegirá al candidato preferido por el votante mediano.
Por tanto, el teorema del votante mediano tiene dos propósitos importantes:
La votación de segunda vuelta instantánea y la pluralidad no cumplen con este criterio, mientras que la votación de aprobación , [1] [2] el método de Coombs y todos los métodos de Condorcet [3] lo satisfacen. En cambio, la votación por puntuación satisface una propiedad del votante promedio (media) estrechamente relacionada y satisface el teorema del votante mediano en la votación estratégica e informada (donde es equivalente a la votación de aprobación ). Los sistemas que no cumplen el criterio del votante medio exhiben un fenómeno de compresión del centro , que fomenta el extremismo en lugar de la moderación.
Harold Hotelling hizo una afirmación similar anteriormente (en 1929) , quien argumentó que los políticos en una democracia representativa convergerían al punto de vista del votante medio, [4] basando esto en su modelo de competencia económica . [4] [5] Sin embargo, esta afirmación se basa en un modelo de votación profundamente simplificado y sólo es parcialmente aplicable a sistemas que satisfacen la propiedad del votante medio. No se puede aplicar en absoluto a sistemas como la votación de segunda vuelta instantánea o la pluralidad. [2]
Consideremos un grupo de votantes que tienen que elegir a uno de un conjunto de dos o más candidatos. Para simplificar, supongamos que el número de votantes es impar.
Las elecciones son unidimensionales . Esto significa que las opiniones tanto de los candidatos como de los votantes se distribuyen a lo largo de un espectro unidimensional, y cada votante clasifica a los candidatos en orden de proximidad, de modo que el candidato más cercano al votante recibe su primera preferencia, el siguiente más cercano recibe su segunda preferencia. preferencia, etcétera.
Un ganador de Condorcet es un candidato preferido por la mayoría de los votantes sobre cualquier otro candidato. En las elecciones generales, es posible que no exista un ganador Condorcet. El teorema del votante mediano dice que:
En el ejemplo anterior, el votante mediano se denota por M y el candidato más cercano a él es C, por lo que el teorema del votante mediano dice que C es el ganador de Condorcet. De ello se deduce que Carlos ganará cualquier elección realizada utilizando un método que satisfaga el criterio de Condorcet. En particular, cuando sólo hay dos candidatos, la regla de la mayoría satisface el criterio de Condorcet; para votaciones multidireccionales, varios métodos lo satisfacen (ver método de Condorcet ).
Bosquejo de prueba : Sea Marlene el votante medio. El candidato más cercano a ella recibirá su primer voto preferencial. Supongamos que este candidato es Charles y que se encuentra a su izquierda. Entonces Marlene y todos los votantes a su izquierda (que representan la mayoría del electorado) preferirán a Carlos a todos los candidatos a su derecha, y Marlene y todos los votantes a su derecha preferirán a Carlos a todos los candidatos a su izquierda.
El teorema fue expuesto por primera vez por Duncan Black en 1948. Escribió que veía una gran brecha en la teoría económica sobre cómo la votación determina el resultado de las decisiones, incluidas las decisiones políticas. El artículo de Black desencadenó una investigación sobre cómo la economía puede explicar los sistemas de votación. En 1957 , Anthony Downs expuso el teorema del votante mediano en su libro Una teoría económica de la democracia . [8]
Diremos que un método de votación tiene la "propiedad del votante mediano en una dimensión" si siempre elige al candidato más cercano al votante mediano bajo un modelo espacial unidimensional. Podemos resumir el teorema del votante mediano diciendo que todos los métodos de Condorcet poseen la propiedad del votante mediano en una dimensión.
Resulta que los métodos de Condorcet no son únicos en esto: el método de Coombs no es consistente con Condorcet pero, aun así, satisface la propiedad del votante mediano en una dimensión. [9] La votación de aprobación satisface la misma propiedad en varios modelos de votación estratégica.
En general, es imposible generalizar el teorema del votante mediano a modelos espaciales en más de una dimensión, aunque se han hecho varios intentos para hacerlo.
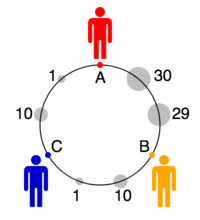
La tabla de la izquierda muestra un ejemplo de una elección dada por el Marqués de Condorcet , quien concluyó que mostraba un problema con el conteo de Borda . [10] : 90 El ganador Condorcet de la izquierda es A, que es preferido a B por 41:40 y a C por 60:21. El ganador de Borda es B. Sin embargo, Donald Saari construye un ejemplo en dos dimensiones donde es el recuento de Borda el que identifica correctamente al candidato más cercano al centro (según lo determinado por la mediana geométrica ). [11]
El diagrama muestra una posible configuración de los votantes y candidatos consistente con las papeletas, con los votantes colocados en la circunferencia de un círculo unitario. En este caso, la desviación absoluta media de A es 1,15, mientras que la de B es 1,09 (y la de C es 1,70), lo que convierte a B en el ganador espacial.
Por tanto, la elección es ambigua en el sentido de que dos representaciones espaciales diferentes implican dos ganadores óptimos diferentes. Ésta es la ambigüedad que buscamos evitar anteriormente al adoptar una métrica mediana para los modelos espaciales; pero aunque la métrica mediana logra su objetivo en una sola dimensión, la propiedad no se generaliza a dimensiones superiores.
A pesar de este resultado, el teorema del votante mediano se puede aplicar a distribuciones que son rotacionalmente simétricas, por ejemplo, gaussianas , que tienen una única mediana que es la misma en todas las direcciones. Siempre que la distribución de votantes tiene una mediana única en todas las direcciones y los votantes clasifican a los candidatos en orden de proximidad, se aplica el teorema del votante mediano: el candidato más cercano a la mediana tendrá una preferencia mayoritaria sobre todos sus rivales y será elegido. por cualquier método de votación que satisfaga la propiedad del votante mediano en una dimensión. [12]
De ello se deduce que todos los métodos de Condorcet (y también el método de Coombs) satisfacen la propiedad del votante mediano en espacios de cualquier dimensión para distribuciones de votantes con medianas omnidireccionales.
Es fácil construir distribuciones de votantes que no tengan una mediana en todas las direcciones. El ejemplo más simple consiste en una distribución limitada a 3 puntos que no están en línea recta, como 1, 2 y 3 en el segundo diagrama. Cada ubicación de votante coincide con la mediana según un determinado conjunto de proyecciones unidimensionales. Si A, B y C son los candidatos, entonces '1' votará por ABC, '2' votará por BCA y '3' votará por CAB, lo que da un ciclo de Condorcet. Este es el tema del teorema de McKelvey-Schofield .
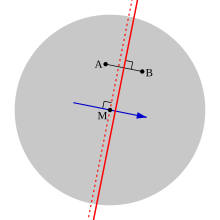
Prueba . Vea el diagrama, en el que el disco gris representa la distribución de votantes uniforme en un círculo y M es la mediana en todas las direcciones. Sean A y B dos candidatos, de los cuales A es el más cercano a la mediana. Entonces los votantes que clasifican a A por encima de B son precisamente los que están a la izquierda (es decir, el lado 'A') de la línea roja continua; y como A está más cerca de M que B, la mediana también está a la izquierda de esta línea.

Ahora bien, como M es mediana en todas las direcciones, coincide con la mediana unidimensional en el caso particular de la dirección que muestra la flecha azul, que es perpendicular a la línea roja continua. Así, si trazamos una línea roja discontinua que pase por M, perpendicular a la flecha azul, entonces podemos decir que la mitad de los votantes se encuentran a la izquierda de esta línea. Pero como esta línea está a la izquierda de la línea roja continua, se deduce que más de la mitad de los votantes clasificarán A por encima de B.
Siempre que existe una mediana omnidireccional única, ésta determina el resultado de los métodos de votación de Condorcet. Al mismo tiempo, podría decirse que se puede identificar a la mediana geométrica como el ganador ideal de una elección de preferencia clasificada (ver comparación de sistemas electorales ). Por tanto, es importante conocer la relación entre ambos. De hecho, siempre que existe una mediana en todas las direcciones (al menos para el caso de distribuciones discretas), coincide con la mediana geométrica.

Lema . Siempre que una distribución discreta tiene una mediana M en todas las direcciones, los puntos de datos que no están ubicados en M deben venir en pares equilibrados ( A , A ') a cada lado de M con la propiedad de que A – M – A ' es una línea recta ( es decir, no como A 0 – M – A 2 en el diagrama).
Prueba . Este resultado fue demostrado algebraicamente por Charles Plott en 1967. [13] Aquí damos una prueba geométrica simple por contradicción en dos dimensiones.
Supongamos, por el contrario, que existe un conjunto de puntos Ai que tienen M como mediana en todas las direcciones, pero para los cuales los puntos que no coinciden con M no vienen en pares equilibrados. Entonces podemos eliminar de este conjunto cualquier punto en M y cualquier par equilibrado alrededor de M , sin que M deje de ser una mediana en cualquier dirección; entonces M sigue siendo una mediana omnidireccional.
Si el número de puntos restantes es impar, entonces podemos trazar fácilmente una línea que pase por M de manera que la mayoría de los puntos se encuentren en un lado de ella, lo que contradice la propiedad mediana de M.
Si el número es par, digamos 2 n , entonces podemos etiquetar los puntos A 0 , A 1 ,... en el sentido de las agujas del reloj alrededor de M comenzando en cualquier punto (ver el diagrama). Sea θ el ángulo subtendido por el arco desde M – A 0 hasta M – A n . Entonces, si θ < 180° como se muestra, podemos dibujar una línea similar a la línea roja discontinua que pasa por M que tiene la mayoría de los puntos de datos en un lado, contradiciendo nuevamente la propiedad mediana de M ; mientras que si θ > 180° lo mismo se aplica con la mayoría de los puntos del otro lado. Y si θ = 180°, entonces A 0 y An forman un par equilibrado , contradiciendo otra suposición.
Teorema . Siempre que una distribución discreta tiene una mediana M en todas las direcciones, coincide con su mediana geométrica.
Prueba . La suma de distancias desde cualquier punto P a un conjunto de puntos de datos en pares equilibrados ( A , A ' ) es la suma de las longitudes A – P – A '. Cada longitud individual de esta forma se minimiza sobre P cuando la línea es recta, como ocurre cuando P coincide con M . La suma de distancias desde P a cualquier punto de datos ubicado en M también se minimiza cuando P y M coinciden. , la suma de distancias desde los puntos de datos a P se minimiza cuando P coincide con M.
Una afirmación más informal –el modelo del votante mediano– está relacionada con el “principio de diferenciación mínima” de Harold Hotelling , también conocido como “ ley de Hotelling ”. Afirma que los políticos gravitan hacia la posición ocupada por el votante medio o, más generalmente, hacia la posición favorecida por el sistema electoral. Fue planteado por primera vez (como una observación, sin ninguna pretensión de rigor) por Hotelling en 1929. [5]
Hotelling veía el comportamiento de los políticos a través de los ojos de un economista. Le llamó la atención el hecho de que las tiendas que venden un determinado bien a menudo se congregan en la misma zona de una ciudad, y vio esto como algo análogo a la convergencia de los partidos políticos. En ambos casos puede ser una política racional para maximizar la participación de mercado .
Como ocurre con cualquier caracterización de la motivación humana, depende de factores psicológicos que no son fácilmente predecibles y está sujeta a muchas excepciones. También depende del sistema de votación: los políticos no convergerán hacia el votante medio a menos que el proceso electoral lo haga. Myerson y Weber demostraron que no se puede esperar que tal resultado ocurra en absoluto en una votación por pluralidad o en una segunda vuelta instantánea . [2]
El teorema es valioso por la luz que arroja sobre la optimización (y los límites de la optimización) de ciertos sistemas de votación.
Valerio Dotti destaca áreas de aplicación más amplias:
El teorema del votante mediano resultó extremadamente popular en la literatura de economía política. La razón principal es que puede adoptarse para derivar implicaciones comprobables sobre la relación entre algunas características de la población votante y el resultado de la política, haciendo abstracción de otras características del proceso político. [12]
Agrega que...
El resultado del votante medio se ha aplicado a una increíble variedad de preguntas. Algunos ejemplos son el análisis de la relación entre la desigualdad de ingresos y el tamaño de la intervención gubernamental en las políticas redistributivas (Meltzer y Richard, 1981), [14] el estudio de los determinantes de las políticas de inmigración (Razin y Sadka, 1999), [15] de la alcance de la tributación sobre diferentes tipos de ingresos (Bassetto y Benhabib, 2006), [16] y muchos más.