En matemáticas , la equivarianza es una forma de simetría para funciones de un espacio con simetría a otro (como los espacios simétricos ). Se dice que una función es una aplicación equivariante cuando su dominio y codominio son afectados por el mismo grupo de simetría , y cuando la función conmuta con la acción del grupo. Es decir, aplicar una transformación de simetría y luego calcular la función produce el mismo resultado que calcular la función y luego aplicar la transformación.
Los mapas equivariantes generalizan el concepto de invariantes , funciones cuyo valor no cambia mediante una transformación de simetría de su argumento. El valor de un mapa equivariante a menudo se denomina (de manera imprecisa) invariante.
En inferencia estadística , la equivarianza bajo transformaciones estadísticas de datos es una propiedad importante de varios métodos de estimación; consulte el estimador invariante para obtener más detalles. En matemáticas puras, la equivarianza es un objeto central de estudio en la topología equivariante y sus subtemas cohomología equivariante y teoría de la homotopía estable equivariante .

En la geometría de los triángulos , el área y el perímetro de un triángulo son invariantes bajo transformaciones euclidianas : trasladar, rotar o reflejar un triángulo no cambia su área ni su perímetro. Sin embargo, los centros de triángulos como el centroide , el circuncentro , el incentro y el ortocentro no son invariantes, porque mover un triángulo también hará que sus centros se muevan. En cambio, estos centros son equivariantes: aplicar cualquier congruencia euclidiana (una combinación de traslación y rotación) a un triángulo y luego construir su centro, produce el mismo punto que construir primero el centro y luego aplicar la misma congruencia al centro. De manera más general, todos los centros de los triángulos también son equivariantes bajo transformaciones de similitud (combinaciones de traslación, rotación, reflexión y escala), [1] y el centroide es equivariante bajo transformaciones afines . [2]
La misma función puede ser invariante para un grupo de simetrías y equivariante para un grupo diferente de simetrías. Por ejemplo, bajo transformaciones de similitud en lugar de congruencias, el área y el perímetro ya no son invariantes: escalar un triángulo también cambia su área y perímetro. Sin embargo, estos cambios ocurren de una manera predecible: si un triángulo se escala por un factor de s , el perímetro también se escala por s y el área se escala por s 2 . De esta manera, la función que asigna cada triángulo a su área o perímetro puede verse como equivariante para una acción grupal multiplicativa de las transformaciones de escala en los números reales positivos.
Otra clase de ejemplos simples proviene de la estimación estadística . La media de una muestra (un conjunto de números reales) se utiliza comúnmente como tendencia central de la muestra. Es equivariante en transformaciones lineales de los números reales, por lo que, por ejemplo, no se ve afectado por la elección de las unidades utilizadas para representar los números. Por el contrario, la media no es equivariante con respecto a transformaciones no lineales como las exponenciales.
La mediana de una muestra es equivariante para un grupo mucho mayor de transformaciones, las funciones (estrictamente) monótonas de los números reales. Este análisis indica que la mediana es más robusta frente a ciertos tipos de cambios en un conjunto de datos y que (a diferencia de la media) es significativa para datos ordinales . [3]
Los conceptos de estimador invariante y estimador equivariante se han utilizado para formalizar este estilo de análisis.
En la teoría de la representación de grupos finitos , un espacio vectorial dotado de un grupo que actúa mediante transformaciones lineales del espacio se denomina representación lineal del grupo. Un mapa lineal que conmuta con la acción se llama entrelazador . Es decir, un entrelazador es simplemente un mapa lineal equivariante entre dos representaciones. Alternativamente, un entrelazador para representaciones de un grupo G sobre un campo K es lo mismo que un homomorfismo de módulo de K [ G ] - módulos , donde K [ G ] es el anillo de grupo de G . [4]
Bajo algunas condiciones, si X e Y son ambas representaciones irreducibles , entonces un entrelazador (distinto del mapa cero ) solo existe si las dos representaciones son equivalentes (es decir, son isomorfas como módulos ). Ese entrelazador es entonces único hasta un factor multiplicativo (un escalar distinto de cero de K ). Estas propiedades se mantienen cuando la imagen de K [ G ] es un álgebra simple, con centro K (por lo que se llama el lema de Schur : ver módulo simple ). Como consecuencia, en casos importantes la construcción de un entrelazador es suficiente para mostrar que las representaciones son efectivamente las mismas. [5]
La equivarianza se puede formalizar utilizando el concepto de conjunto G para un grupo G. Este es un objeto matemático que consta de un conjunto matemático S y una acción grupal (a la izquierda) de G sobre S. Si X e Y son ambos conjuntos G para el mismo grupo G , entonces se dice que una función f : X → Y es equivariante si
para todo g ∈ G y todo x en X . [6]
Si una o ambas acciones son correctas, la condición de equivarianza podrá modificarse adecuadamente:
Los mapas equivariantes son homomorfismos en la categoría de G -conjuntos (para un G fijo ). [7] De ahí que también se les conozca como G -morfismos , [7] G -maps , [8] o G -homomorfismos . [9] Los isomorfismos de conjuntos G son simplemente mapas equivariantes biyectivos . [7]
La condición de equivarianza también puede entenderse como el siguiente diagrama conmutativo . Tenga en cuenta que denota el mapa que toma un elemento y devuelve .
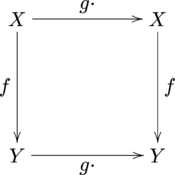
Los mapas equivalentes se pueden generalizar a categorías arbitrarias de forma sencilla. Cada grupo G puede verse como una categoría con un solo objeto ( los morfismos en esta categoría son solo los elementos de G ). Dada una categoría arbitraria C , una representación de G en la categoría C es un functor de G a C. Tal funtor selecciona un objeto de C y un subgrupo de automorfismos de ese objeto. Por ejemplo, un conjunto G es equivalente a un funtor de G a la categoría de conjuntos , Set , y una representación lineal es equivalente a un funtor de la categoría de espacios vectoriales sobre un campo , Vect K.
Dadas dos representaciones, ρ y σ, de G en C , una aplicación equivariante entre esas representaciones es simplemente una transformación natural de ρ a σ. Usando transformaciones naturales como morfismos , se puede formar la categoría de todas las representaciones de G en C. Esta es solo la categoría de functor C G.
Para otro ejemplo, tomemos C = Top , la categoría de espacios topológicos . Una representación de G en Top es un espacio topológico sobre el cual G actúa continuamente . Una aplicación equivariante es entonces una aplicación continua f : X → Y entre representaciones que conmuta con la acción de G .