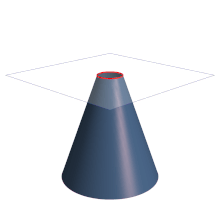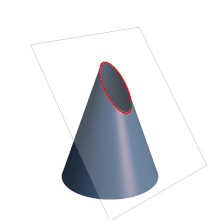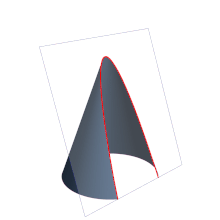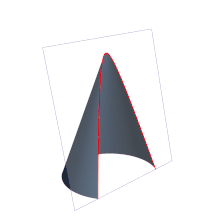
Elipse

[2]​ Su excentricidad es inferior a la unidad, no tiene puntos impropios por lo que nos encontramos ante una curva cerrada.

La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Pérgamo.

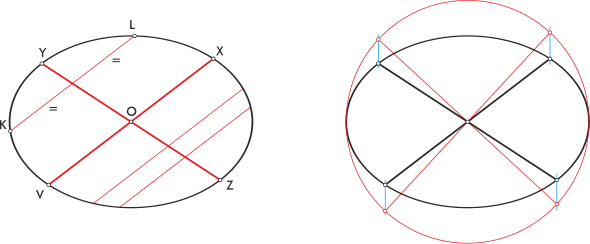
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor.

Existen varios métodos para hallar los diámetros principales a partir de los conjugados.

Trazamos una perpendicular al diámetro mayor por un foco hasta la circunferencia principal, dibujamos por el punto de corte una tangente a dicha circunferencia; en el lugar donde esa tangente encuentra la prolongación del diámetro mayor está la directriz, que es perpendicular al diámetro mayor.

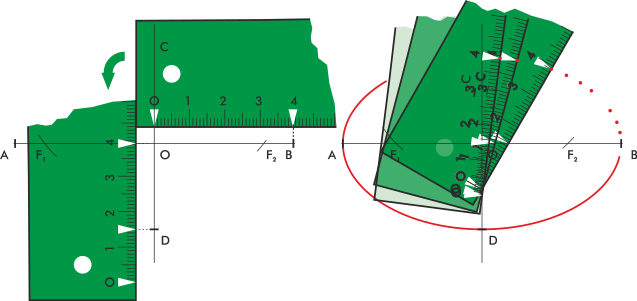
Con la cuerda tensa se mueve el lápiz o material de dibujo rodeando por completo los dos focos.

Se denomina “del jardinero” a este método porque sirve para trazar en el suelo elipses de gran tamaño y precisión suficiente, con medios modestos.

Dibujados los dos ejes principales, se toma con el compás la medida a de la mitad del eje mayor.

A continuación tomamos el resto de la medida del eje mayor, desde el punto (1) al otro extremo (B), y con esa medida, haciendo centro de nuevo en los focos, cruzamos los arcos trazados antes.

Repitiendo la operación tantas veces como sea necesario obtenemos puntos de la elipse.

Se completa el dibujo a mano o mediante plantillas de curvas.

Para construirla con reglas y compás marcamos puntos arbitrarios en el eje menor.

Sobre esas rectas, con el compás y desde cada punto del eje mayor, tomamos la medida de la mitad del eje menor, marcándola sobre la línea, lo que nos da los puntos de la elipse.

Existe una máquina sencilla (un elipsógrafo) hecha a base de guías o raíles y barras y llamada compás de Arquímedes, que se basa en este principio.

Desde el extremo del radio trazamos una recta auxiliar, paralela al eje menor, hacia dentro de la circunferencia.

Desde el punto donde el radio corta la circunferencia menor trazamos una recta auxiliar paralela al eje mayor, que cruce la línea auxiliar que acabamos de hacer.

Normalmente por comodidad el dibujo se sistematiza; en lugar de los radios dibujamos diámetros completos, los trazos auxiliares verticales y horizontales se hacen de una vez mediante paralelas a los ejes.

Una construcción corriente para dibujar una elipse o un arco de elipse en un paralelogramo es hacerlo afín a otro ortogonal en el que podamos trazar un arco de circunferencia o una circunferencia completa.

Esto es útil en particular para elipses proyectadas en axonométrica u otra proyección cilíndrica.

Es importante señalar que en axonométrica este procedimiento no equivale en general a un abatimiento.

En la segunda imagen vemos el mismo procedimiento aplicado a dos diámetros conjugados; el rectángulo se hace romboide, pero sigue funcionando la construcción como una proyección afín de la otra.

Vamos uniendo en orden cada punto correspondiente como se ve en la imagen, desde los extremos el eje mayor.

Los puntos que se cortan de las rectas correspondientes pertenecen a la elipse.

El término anamorfosis proviene del idioma griego y significa trasformar.

Este procedimiento era muy utilizado para realizar perspectivas ilusionistas, anamórficas, llamadas trampantojos.

sea concordante con el ángulo polar respecto al centro desplazado

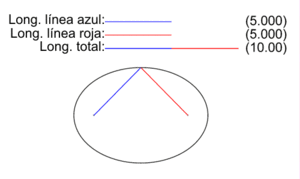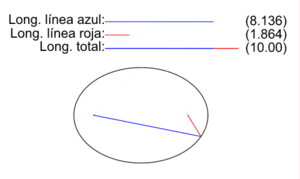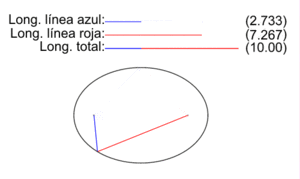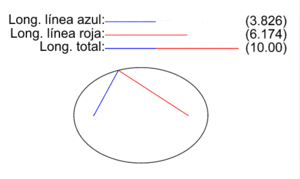
Sin embargo, el matemático Ramanujan dio una expresión sencilla que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas.

Teorema: Si la intersección de una recta con la corona comprendida entre dos elipses semejantes con el mismo centro y ejes correspondientes colineales consta de dos segmentos, entonces éstos tienen igual longitud.

Contrayendo o dilatando uniformemente una de las direcciones coordenadas, mediante anamorfosis, podemos transformar cualquier caso en este caso particular, pues todos los segmentos con la misma pendiente cambian su longitud en la misma proporción.

Esto ocurre porque las palabras se transmiten por al aire mediante ondas y llegan a algún lugar.