Epiciclo
En el modelo geocéntrico estos datos implican que el planeta se mueve en círculos además de orbitar la Tierra y los datos suponen que cada planeta tiene diferentes velocidades y diámetros en sus epiciclos respectivos.
El epiciclo gira y rota a lo largo del deferente con un movimiento uniforme.
Fue el uso de ese ecuante lo que distinguía al sistema ptolemaico.
Ptolomeo no predijo los tamaños relativos de los deferentes planetarios en el Almagesto.
Cada noche, el planeta aparecería "desfasado" un poco por detrás de las estrellas próximas, en lo que se llama movimiento progrado.
La regularidad en los movimientos de los cuerpos errantes sugería que sus posiciones podrían ser predecibles.
Sin embargo, Aristarco de Samos especuló que los planetas orbitaban el Sol.
Empero, le faltaban herramientas matemáticas y ópticas, que llegaron mucho después, en la Modernidad.
Por otra parte, la física aristotélica afirmaba con énfasis la tesis de que el mundo supralunar era perfecto y que, por ello, los cuerpos celestes solo podían desplazarse con movimientos circulares y uniformes.
A continuación, Johannes Kepler, tomando las observaciones de Tycho Brahe, pudo formular sus famosas tres leyes del movimiento planetario y describió las órbitas de los planetas del sistema solar con una precisión increíble nunca antes vista.
Apolonio de Perga se dio cuenta de que esta variación cíclica podría representarse visualmente por pequeñas órbitas circulares o epiciclos, que giraban en órbitas circulares más grandes, o deferentes.
Hiparco de Nicea calculó las órbitas necesarias y añadió que el centro de los deferentes no coincidía con la Tierra, considerada el centro del universo, sino que eran excéntricos.
Owen Gingerich[2] describió una conjunción planetaria ocurrida en 1504 que aparentemente observó Copérnico.
Usando modernos programas informáticos, Gingerich descubrió que, en el momento de la conjunción, Saturno, en efecto, iba rezagado según las tablas en un grado y medio y Marte fallaba en las predicciones en casi dos grados.
Sin embargo, encontró que las predicciones de Ptolomeo para Júpiter eran al mismo tiempo bastante precisas.
Cuando Copérnico transformó las observaciones realizadas desde la Tierra a coordenadas heliocéntricas,[3] se encontró con un problema totalmente nuevo.
Mientras trabajaba con las matemáticas, sin embargo, descubrió que sus modelos podían combinarse en un sistema unificado.
Mercurio orbitaba más cercano al Sol y la posición del resto de los planetas se desplazó hacia el espacio exterior, dispuestas sus órbitas en distancias proporcionales a sus períodos de revolución.
Varios libros del siglo XVI basados en Ptolomeo y Copérnico utilizan aproximadamente el mismo número de epiciclos.
Empero, cuando publicó De revolutionibus orbium coelestium, ya había añadido más círculos.
[10] La referencia popular de unos 80 círculos para el sistema ptolomeico parece haber surgido en 1898.
Los trabajos de Copérnico proporcionaban explicaciones a fenómenos como el movimiento retrógrado, pero realmente no probaban que los planetas giraran alrededor del Sol.
Este modelo funcionaba tan bien como lo hizo debido a la extraordinaria estabilidad orbital del sistema solar.
La mecánica clásica o newtoniana eliminó la necesidad de métodos deferente-epiciclo y produjo teorías mucho más poderosas.
El más complejo problema de los n cuerpos requiere métodos numéricos para su solución.
Se creía erróneamente que se añadieron más niveles de epiciclos (círculos dentro de círculos) a los modelos para que coincidiesen con mayor precisión con los movimientos planetarios observados.
Las Tablas alfonsinas, por ejemplo, se calcularon aparentemente utilizando los métodos originales de Ptolomeo sin adornos.
Los astrónomos experimentados habrían conocido estas deficiencias y habían recurrido a atajos para resolverlos.
Puede usarse, por ejemplo, para describir el continuo ajuste de una teoría para hacer predicciones que coincidan con los hechos.
Esto se debe a que los epiciclos pueden representarse como series de Fourier complejas; así que, con un amplio número de epiciclos, las trayectorias muy complicadas pueden representarse en el plano complejo.



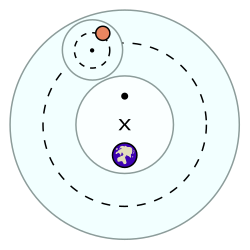
* El centro del deferente es X , pero el movimiento angular del epiciclo es aparentemente acorde solo respecto al punto ( · ) que es el ecuante.
* El deferente es el recorrido circular que describe el centro del epiciclo.
* El ecuante es el punto en torno al cual se mueve el planeta en su trayectoria, aparentemente.