

En matemáticas , una variedad es un espacio topológico que localmente se parece al espacio euclidiano cerca de cada punto. Más precisamente, una variedad -dimensional, o -variedad para abreviar, es un espacio topológico con la propiedad de que cada punto tiene una vecindad que es homeomorfa a un subconjunto abierto del espacio euclidiano -dimensional.
Las variedades unidimensionales incluyen líneas y círculos , pero no curvas que se cruzan solas, como la figura 8 . Las variedades bidimensionales también se llaman superficies . Los ejemplos incluyen el plano , la esfera y el toroide , y también la botella de Klein y el plano proyectivo real .
El concepto de variedad es fundamental para muchas partes de la geometría y la física matemática moderna porque permite describir estructuras complicadas en términos de propiedades topológicas bien entendidas de espacios más simples. Las variedades surgen naturalmente como conjuntos solución de sistemas de ecuaciones y como gráficas de funciones. El concepto tiene aplicaciones en gráficos por computadora dada la necesidad de asociar imágenes con coordenadas (por ejemplo, tomografías computarizadas ).
Los colectores pueden equiparse con estructura adicional. Una clase importante de variedades son las variedades diferenciables ; su estructura diferenciable permite realizar cálculos . Una métrica de Riemann en una variedad permite medir distancias y ángulos . Las variedades simplécticas sirven como espacios de fase en el formalismo hamiltoniano de la mecánica clásica , mientras que las variedades lorentzianas de cuatro dimensiones modelan el espacio-tiempo en la relatividad general .
El estudio de variedades requiere conocimientos prácticos de cálculo y topología .

Después de una línea, un círculo es el ejemplo más simple de variedad topológica. La topología ignora la flexión, por lo que una pequeña porción de un círculo se trata de la misma manera que una pequeña porción de una línea. Considerando, por ejemplo, la parte superior del círculo unitario , x 2 + y 2 = 1, donde la coordenada y es positiva (indicada por el arco amarillo en la Figura 1 ). Cualquier punto de este arco puede describirse de forma única mediante su coordenada x . Entonces, la proyección sobre la primera coordenada es un mapeo continuo e invertible desde el arco superior hasta el intervalo abierto (−1, 1):
Estas funciones, junto con las regiones abiertas que mapean, se denominan gráficos . De manera similar, hay gráficos para las partes inferior (roja), izquierda (azul) y derecha (verde) del círculo:
Juntas, estas partes cubren todo el círculo y los cuatro gráficos forman un atlas del círculo.
Los gráficos superior y derecho, y respectivamente, se superponen en su dominio: su intersección se encuentra en el cuarto del círculo donde ambas coordenadas y son positivas. Ambos asignan esta parte al intervalo , aunque de manera diferente. Por lo tanto, se puede construir una función que toma valores del codominio de regreso al círculo usando la inversa, seguido de regreso al intervalo. Si a es cualquier número en , entonces:
Esta función se llama mapa de transición .
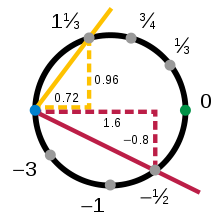
Los gráficos superior, inferior, izquierdo y derecho no forman el único atlas posible. Los gráficos no tienen por qué ser proyecciones geométricas y el número de gráficos es una cuestión de elección. Considere los gráficos
Aquí s es la pendiente de la línea que pasa por el punto en las coordenadas ( x , y ) y el punto de pivote fijo (−1, 0); de manera similar, t es lo opuesto a la pendiente de la línea que pasa por los puntos en las coordenadas ( x , y ) y (+1, 0). La aplicación inversa de s a ( x , y ) viene dada por
Se puede confirmar que x 2 + y 2 = 1 para todos los valores de s y t . Estos dos mapas proporcionan un segundo atlas para el círculo, con el mapa de transición
Cada gráfico omite un solo punto, ya sea (−1, 0) para s o (+1, 0) para t , por lo que ninguno de los gráficos por sí solo es suficiente para cubrir todo el círculo. Se puede demostrar que no es posible cubrir el círculo completo con un solo gráfico. Por ejemplo, aunque es posible construir un círculo a partir de un intervalo de una sola línea superponiendo y "pegando" los extremos, esto no produce un gráfico; una parte del círculo se asignará a ambos extremos a la vez, perdiendo invertibilidad.
La esfera es un ejemplo de superficie. La esfera unitaria de la ecuación implícita.
puede estar cubierto por un atlas de seis cartas : el plano z = 0 divide la esfera en dos medias esferas ( z > 0 y z < 0 ), que pueden representarse ambas en el disco x 2 + y 2 < 1 mediante la proyección en el plano de coordenadas xy . Esto proporciona dos gráficos; los otros cuatro gráficos se obtienen mediante una construcción similar con los otros dos planos de coordenadas.
Al igual que con el círculo, se puede definir un gráfico que cubra toda la esfera excluyendo un punto. Por tanto, dos cartas son suficientes, pero la esfera no puede ser cubierta por una sola carta.
Este ejemplo es históricamente significativo, ya que ha motivado la terminología; Se hizo evidente que toda la superficie de la Tierra no puede tener una representación plana que consista en un solo mapa (también llamado "carta", ver carta náutica ), y por lo tanto se necesitan atlas para cubrir toda la superficie de la Tierra.

No es necesario conectar los colectores (todos en "una sola pieza"); un ejemplo es un par de círculos separados.
No es necesario cerrar los colectores ; por tanto, un segmento de recta sin sus puntos finales es una variedad. Nunca son contables , a menos que la dimensión de la variedad sea 0. Juntando estas libertades, otros ejemplos de variedades son una parábola , una hipérbola y el lugar geométrico de los puntos en una curva cúbica y 2 = x 3 − x (un circuito cerrado pieza y una pieza abierta e infinita).
Sin embargo, se excluyen ejemplos como dos círculos que se tocan y que comparten un punto para formar una figura de 8; en el punto compartido, no se puede crear un gráfico satisfactorio. Incluso con la curvatura permitida por la topología, la vecindad del punto compartido parece un "+", no una línea. Un "+" no es homeomorfo a un segmento de línea, ya que eliminar el punto central del "+" da un espacio con cuatro componentes (es decir, piezas), mientras que eliminar un punto de un segmento de línea da un espacio con como máximo dos piezas; Las operaciones topológicas siempre preservan el número de piezas.
Informalmente, una variedad es un espacio que está "modelado sobre" el espacio euclidiano.
Hay muchos tipos diferentes de variedades. En geometría y topología , todas las variedades son variedades topológicas , posiblemente con estructura adicional. Se puede construir una variedad dando una colección de gráficos de coordenadas, es decir, una cobertura de conjuntos abiertos con homeomorfismos a un espacio euclidiano y funciones de parche [ aclaración necesaria ] : homeomorfismos de una región del espacio euclidiano a otra región si corresponden a la misma parte de la variedad en dos gráficos de coordenadas diferentes. A una variedad se le puede dar una estructura adicional si las funciones de parcheo satisfacen axiomas más allá de la continuidad. Por ejemplo, las variedades diferenciables tienen homeomorfismos en vecindades superpuestas difeomorfas entre sí, de modo que la variedad tiene un conjunto bien definido de funciones que son diferenciables en cada vecindad, por lo tanto diferenciables en la variedad en su conjunto.
Formalmente, una variedad (topológica) es un segundo espacio de Hausdorff contable que es localmente homeomorfo a un espacio euclidiano.
El segundo contable y Hausdorff son condiciones puntuales ; el segundo contable excluye espacios que son en algún sentido "demasiado grandes", como la línea larga , mientras que Hausdorff excluye espacios como "la línea con dos orígenes" (estas generalizaciones de variedades se analizan en variedades que no son de Hausdorff ).
Localmente homeomorfo a un espacio euclidiano significa que cada punto tiene una vecindad homeomorfa a un subconjunto abierto del espacio euclidiano para algún entero no negativo n .
Esto implica que el punto es un punto aislado (si ), o tiene una vecindad homeomorfa a la bola abierta.
La n que aparece en la definición anterior se llama dimensión local de la variedad. Generalmente se considera que las variedades tienen una dimensión local constante, y la dimensión local se denomina dimensión de la variedad. Éste es especialmente el caso cuando se conectan colectores . Sin embargo, algunos autores admiten variedades que no están conexas y donde diferentes puntos pueden tener diferentes dimensiones . [1] Si una variedad tiene una dimensión fija, esto se puede enfatizar llamándolamúltiple puro . Por ejemplo, la (superficie de una) esfera tiene una dimensión constante de 2 y, por lo tanto, es una variedad pura, mientras que launión disjuntade una esfera y una línea en el espacio tridimensionalnouna variedad pura. Dado que la dimensión es una invariante local (es decir, el mapa que envía cada punto a la dimensión de su vecindad sobre la cual se define un gráfico eslocalmente constante), cadacomponente conectadotiene una dimensión fija.
Teóricamente , una variedad es un espacio localmente anillado , cuya estructura es localmente isomorfa al haz de funciones continuas (o diferenciables, o analíticas complejas, etc.) en el espacio euclidiano . Esta definición se utiliza principalmente cuando se analizan variedades analíticas en geometría algebraica .
La Tierra esférica se navega utilizando mapas o cartas planas, recopiladas en un atlas. De manera similar, una variedad se puede describir utilizando mapas matemáticos , llamados gráficos de coordenadas , recopilados en un atlas matemático . Generalmente no es posible describir una variedad con un solo gráfico, porque la estructura global de la variedad es diferente de la estructura simple de los gráficos. Por ejemplo, ningún mapa plano puede representar toda la Tierra sin separación de entidades adyacentes a través de los límites del mapa o duplicación de cobertura. Cuando se construye una variedad a partir de múltiples gráficos superpuestos, las regiones donde se superponen contienen información esencial para comprender la estructura global.
Un mapa de coordenadas , un gráfico de coordenadas o simplemente un gráfico de una variedad es un mapa invertible entre un subconjunto de la variedad y un espacio simple tal que tanto el mapa como su inverso preservan la estructura deseada. [2] Para una variedad topológica, el espacio simple es un subconjunto de algún espacio euclidiano y el interés se centra en la estructura topológica. Esta estructura se conserva mediante homeomorfismos , mapas invertibles que son continuos en ambas direcciones.
En el caso de una variedad diferenciable, un conjunto de gráficos llamado atlas , cuyas funciones de transición (ver más abajo) son todas diferenciables, nos permite hacer cálculos sobre ella. Las coordenadas polares , por ejemplo, forman un gráfico para el plano menos el eje x positivo y el origen. Otro ejemplo de gráfico es el mapa χ arriba mencionado anteriormente, un gráfico para el círculo.
La descripción de la mayoría de los colectores requiere más de un gráfico. Una colección específica de cartas que cubre una variedad se llama atlas . Un atlas no es único, ya que todas las variedades se pueden cubrir de múltiples maneras utilizando diferentes combinaciones de gráficos. Se dice que dos atlas son equivalentes si su unión es también un atlas.
El atlas que contiene todas las cartas posibles consistentes con un atlas dado se llama atlas máximo (es decir, una clase de equivalencia que contiene ese atlas dado). A diferencia de un atlas ordinario, el atlas máximo de una variedad determinada es único. Aunque es útil para definiciones, es un objeto abstracto y no se utiliza directamente (por ejemplo, en cálculos).
Las cartas de un atlas pueden superponerse y un único punto de una variedad puede representarse en varias cartas. Si dos cartas se superponen, partes de ellas representan la misma región de la variedad, del mismo modo que un mapa de Europa y un mapa de Rusia pueden contener Moscú. Dados dos gráficos superpuestos, se puede definir una función de transición que va de una bola abierta al colector y luego regresa a otra (o quizás la misma) bola abierta . El mapa resultante, como el mapa T en el ejemplo del círculo anterior, se llama cambio de coordenadas , transformación de coordenadas , función de transición o mapa de transición .
También se puede utilizar un atlas para definir una estructura adicional en el colector. La estructura se define primero en cada gráfico por separado. Si todos los mapas de transición son compatibles con esta estructura, la estructura se transfiere a la variedad.
Esta es la forma estándar en que se definen las variedades diferenciables. Si las funciones de transición de un atlas para una variedad topológica preservan la estructura diferencial natural de (es decir, si son difeomorfismos ), la estructura diferencial se transfiere a la variedad y la convierte en una variedad diferenciable. Las variedades complejas se introducen de manera análoga al requerir que las funciones de transición de un atlas sean funciones holomorfas . Para variedades simplécticas , las funciones de transición deben ser simplectomorfismos .
La estructura de la variedad depende del atlas, pero a veces se puede decir que diferentes atlas dan lugar a la misma estructura. Estos atlas se denominan compatibles .
Estas nociones se precisan en general mediante el uso de pseudogrupos .
Una variedad con límite es una variedad con arista. Por ejemplo, una hoja de papel es una variedad bidimensional con un límite unidimensional. El límite de una variedad con límite es una variedad. Un disco (círculo más interior) es una variedad de 2 con límite. Su límite es un círculo, una variedad 1 . Un cuadrado con interior también es una variedad de 2 con límite. Una bola (esfera más interior) es una variedad de 3 con límite. Su límite es una esfera, una variedad 2. (No confundir con Límite (topología) ).
En lenguaje técnico, una variedad con límite es un espacio que contiene tanto puntos interiores como puntos límite. Cada punto interior tiene una vecindad homeomorfa a la bola abierta . Cada punto límite tiene una vecindad homeomorfa a la "media" -bola . Cualquier homeomorfismo entre medias bolas debe enviar puntos con a puntos con . Esta invariancia permite "definir" puntos límite; ver el siguiente párrafo.
Sea una variedad con límite. El interior de , denotado , es el conjunto de puntos en los que tienen vecindades homeomorfas a un subconjunto abierto de . El límite de , denotado , es el complemento de in . Los puntos límite se pueden caracterizar como aquellos puntos que aterrizan en el hiperplano límite bajo algún gráfico de coordenadas.
Si es una variedad con límite de dimensión , entonces es una variedad (sin límite) de dimensión y es una variedad (sin límite) de dimensión .
Una sola variedad se puede construir de diferentes maneras, cada una de las cuales enfatiza un aspecto diferente de la variedad, lo que lleva a un punto de vista ligeramente diferente.

Quizás la forma más sencilla de construir una variedad sea la utilizada en el ejemplo anterior del círculo. Primero, se identifica un subconjunto y luego se construye un atlas que cubre este subconjunto. El concepto de variedad surgió históricamente a partir de construcciones como ésta. Aquí hay otro ejemplo, aplicando este método a la construcción de una esfera:
Una esfera se puede tratar casi de la misma manera que un círculo. En matemáticas una esfera es sólo la superficie (no el interior sólido), que puede definirse como un subconjunto de :
La esfera es bidimensional, por lo que cada gráfico asignará parte de la esfera a un subconjunto abierto de . Considere el hemisferio norte, que es la parte con la coordenada z positiva (coloreada en rojo en la imagen de la derecha). La función χ definida por
asigna el hemisferio norte al disco unitario abierto proyectándolo en el plano ( x , y ). Existe un gráfico similar para el hemisferio sur. Junto con dos cartas proyectadas en el plano ( x , z ) y dos cartas proyectadas en el plano ( y , z ), se obtiene un atlas de seis cartas que cubre toda la esfera.
Esto se puede generalizar fácilmente a esferas de dimensiones superiores.
Se puede construir una variedad pegando piezas de manera consistente, convirtiéndolas en gráficos superpuestos. Esta construcción es posible para cualquier variedad y, por lo tanto, se utiliza a menudo como caracterización, especialmente para variedades diferenciables y riemannianas. Se centra en un atlas, ya que los parches proporcionan naturalmente gráficos, y dado que no hay espacio exterior involucrado, conduce a una vista intrínseca de la variedad.
La variedad se construye especificando un atlas, que a su vez está definido por mapas de transición. Por lo tanto, un punto de la variedad es una clase de equivalencia de puntos que se asignan entre sí mediante aplicaciones de transición. Los gráficos asignan clases de equivalencia a puntos de un solo parche. Generalmente existen fuertes exigencias sobre la coherencia de los mapas de transición. Para variedades topológicas se requiere que sean homeomorfismos; si también son difeomorfismos, la variedad resultante es una variedad diferenciable.
Esto se puede ilustrar con el mapa de transición t = 1 ⁄ s de la segunda mitad del ejemplo del círculo. Comience con dos copias de la línea. Utilice la coordenada s para la primera copia y t para la segunda copia. Ahora, pegue ambas copias identificando el punto t en la segunda copia con el punto s = 1 ⁄ t en la primera copia (los puntos t = 0 y s = 0 no están identificados con ningún punto en la primera y segunda copia, respectivamente). Esto da un círculo.
La primera construcción y esta construcción son muy similares, pero representan puntos de vista bastante diferentes. En la primera construcción, la variedad se ve incrustada en algún espacio euclidiano. Esta es la visión extrínseca . Cuando una variedad se ve de esta manera, es fácil utilizar la intuición de los espacios euclidianos para definir una estructura adicional. Por ejemplo, en un espacio euclidiano, siempre está claro si un vector en algún punto es tangencial o normal a alguna superficie que pasa por ese punto.
La construcción de mosaico no utiliza ninguna incrustación, sino que simplemente ve la variedad como un espacio topológico en sí mismo. Este punto de vista abstracto se llama visión intrínseca . Puede hacer que sea más difícil imaginar qué podría ser un vector tangente, y no existe una noción intrínseca de un paquete normal , sino que existe un paquete normal estable intrínseco .
La n -esfera S n es una generalización de la idea de círculo (1 esfera) y esfera (2 esferas) a dimensiones superiores. Se puede construir una n -esfera S n pegando dos copias de . El mapa de transición entre ellos es la inversión en una esfera , definida como
Esta función es su propia inversa y, por tanto, se puede utilizar en ambas direcciones. Como el mapa de transición es una función suave , este atlas define una variedad suave. En el caso n = 1, el ejemplo se simplifica al ejemplo del círculo dado anteriormente.
Es posible definir diferentes puntos de una variedad para que sean iguales. Esto se puede visualizar como unir estos puntos en un solo punto, formando un espacio cociente . Sin embargo, no hay razón para esperar que tales espacios cocientes sean múltiples. Entre los posibles espacios de cociente que no son necesariamente variedades, se considera que los orbifolds y los complejos CW se comportan relativamente bien . Un ejemplo de espacio cociente de una variedad que también lo es es el espacio proyectivo real , identificado como espacio cociente de la esfera correspondiente.
Un método para identificar puntos (pegarlos) es mediante una acción derecha (o izquierda) de un grupo , que actúa sobre la variedad. Se identifican dos puntos si algún elemento del grupo mueve uno sobre el otro. Si M es la variedad y G es el grupo, el espacio cociente resultante se denota por M / G (o G \ M ).
Las variedades que se pueden construir identificando puntos incluyen toros y espacios proyectivos reales (comenzando con un plano y una esfera, respectivamente).
Se pueden pegar dos variedades con límites a lo largo de un límite. Si esto se hace de la manera correcta, el resultado también es múltiple. De manera similar, se pueden pegar dos límites de una sola variedad.
Formalmente, el pegado se define por una biyección entre los dos límites [ dudoso ] . Se identifican dos puntos cuando se asignan entre sí. Para una variedad topológica, esta biyección debe ser un homeomorfismo; de lo contrario, el resultado no será una variedad topológica. De manera similar, para una variedad diferenciable, tiene que ser un difeomorfismo. Para otras variedades, se deben conservar otras estructuras.
Un cilindro finito se puede construir como una variedad comenzando con una tira [0,1] × [0,1] y pegando un par de bordes opuestos en el límite mediante un difeomorfismo adecuado. Se puede obtener un plano proyectivo pegando una esfera con un agujero a una tira de Möbius a lo largo de sus respectivos límites circulares.
El producto cartesiano de variedades también es una variedad.
La dimensión de la variedad de productos es la suma de las dimensiones de sus factores. Su topología es la topología del producto , y un producto cartesiano de gráficos es un gráfico para la variedad de productos. Por lo tanto, se puede construir un atlas para la variedad de productos utilizando atlas para sus factores. Si estos atlas definen una estructura diferencial sobre los factores, el atlas correspondiente define una estructura diferencial sobre la variedad de productos. Lo mismo ocurre con cualquier otra estructura definida sobre los factores. Si uno de los factores tiene un límite, la variedad de productos también tiene un límite. Los productos cartesianos se pueden utilizar para construir toros y cilindros finitos , por ejemplo, como S 1 × S 1 y S 1 × [0,1], respectivamente.

El estudio de variedades combina muchas áreas importantes de las matemáticas: generaliza conceptos como curvas y superficies, así como ideas del álgebra lineal y la topología.
Antes del concepto moderno de variedad hubo varios resultados importantes.
La geometría no euclidiana considera espacios donde falla el postulado de las paralelas de Euclides . Saccheri estudió por primera vez tales geometrías en 1733, pero sólo intentó refutarlas. Gauss , Bolyai y Lobachevsky los descubrieron de forma independiente 100 años después. Su investigación descubrió dos tipos de espacios cuyas estructuras geométricas difieren de la del espacio euclidiano clásico; estos dieron lugar a la geometría hiperbólica y la geometría elíptica . En la teoría moderna de las variedades, estas nociones corresponden a variedades de Riemann con curvatura negativa y positiva constante , respectivamente.
Carl Friedrich Gauss pudo haber sido el primero en considerar los espacios abstractos como objetos matemáticos por derecho propio. Su teorema egregium proporciona un método para calcular la curvatura de una superficie sin considerar el espacio ambiental en el que se encuentra la superficie. Una superficie así se llamaría, en terminología moderna, variedad; y en términos modernos, el teorema demostró que la curvatura de la superficie es una propiedad intrínseca . La teoría múltiple ha llegado a centrarse exclusivamente en estas propiedades intrínsecas (o invariantes), ignorando en gran medida las propiedades extrínsecas del espacio ambiental.
Otro ejemplo más topológico de una propiedad intrínseca de una variedad es su característica de Euler . Leonhard Euler demostró que para un politopo convexo en el espacio euclidiano tridimensional con V vértices (o esquinas), E aristas y F caras,
Las investigaciones de Niels Henrik Abel y Carl Gustav Jacobi sobre la inversión de integrales elípticas en la primera mitad del siglo XIX los llevaron a considerar tipos especiales de variedades complejas, ahora conocidas como jacobianas . Bernhard Riemann contribuyó aún más a su teoría, aclarando el significado geométrico del proceso de continuación analítica de funciones de variables complejas.
Otra fuente importante de variedades en las matemáticas del siglo XIX fue la mecánica analítica , desarrollada por Siméon Poisson , Jacobi y William Rowan Hamilton . Se cree que los posibles estados de un sistema mecánico son puntos de un espacio abstracto, espacio de fases en los formalismos lagrangiano y hamiltoniano de la mecánica clásica. Este espacio es, de hecho, una variedad de alta dimensión, cuya dimensión corresponde a los grados de libertad del sistema y donde los puntos están especificados por sus coordenadas generalizadas . Para un movimiento ilimitado de partículas libres, la variedad es equivalente al espacio euclidiano, pero varias leyes de conservación la limitan a formaciones más complicadas, por ejemplo, los tori de Liouville. La teoría de un cuerpo sólido en rotación, desarrollada en el siglo XVIII por Leonhard Euler y Joseph-Louis Lagrange , ofrece otro ejemplo en el que la variedad no es trivial. Henri Poincaré , uno de los fundadores de la topología, enfatizó los aspectos geométricos y topológicos de la mecánica clásica .
Riemann fue el primero en realizar un extenso trabajo generalizando la idea de superficie a dimensiones superiores. El nombre variedad proviene del término alemán original de Riemann, Mannigfaltigkeit , que William Kingdon Clifford tradujo como "multiplicidad". En su conferencia inaugural en Gotinga, Riemann describió el conjunto de todos los valores posibles de una variable con ciertas restricciones como Mannigfaltigkeit , porque la variable puede tener muchos valores. Distingue entre stetige Mannigfaltigkeit y diskrete Mannigfaltigkeit ( variedad continua y variedad discontinua ), dependiendo de si el valor cambia continuamente o no. Como ejemplos continuos, Riemann se refiere no sólo a los colores y la ubicación de los objetos en el espacio, sino también a las posibles formas de una figura espacial. Usando inducción , Riemann construye una n-fach ausgedehnte Mannigfaltigkeit ( n veces variedad extendida o variedad n-dimensional ) como una pila continua de (n−1) variedades dimensionales. La noción intuitiva de Riemann de Mannigfaltigkeit evolucionó hasta convertirse en lo que hoy se formaliza como una variedad. Las variedades de Riemann y las superficies de Riemann llevan el nombre de Riemann.
En su muy influyente artículo, Analysis Situs , [4] Henri Poincaré dio una definición de variedad diferenciable ( variété ) que sirvió como precursora del concepto moderno de variedad. [5]
En la primera sección de Análisis Situs, Poincaré define una variedad como el conjunto de niveles de una función continuamente diferenciable entre espacios euclidianos que satisface la hipótesis de no degeneración del teorema de la función implícita . En la tercera sección, comienza señalando que la gráfica de una función continuamente diferenciable es una variedad en el último sentido. Luego propone una nueva definición, más general, de variedad basada en una "cadena de variedades" ( une chaîne des variétés ).
La noción de Poincaré de una cadena de variedades es precursora de la noción moderna de atlas. En particular, considera dos variedades definidas respectivamente como gráficas de funciones y . Si estas variedades se superponen ( a une partie commune ), entonces requiere que las coordenadas dependan continuamente de manera diferenciable de las coordenadas y viceversa (' ...les sont fonctions analytiques des et inversement '). De esta manera introduce un precursor de la noción de gráfico y de mapa de transición.
Por ejemplo, el círculo unitario en el plano puede considerarse como la gráfica de la función o bien como la función en una vecindad de cada punto excepto los puntos (1, 0) y (−1, 0); y en una vecindad de esos puntos, se puede considerar como la gráfica de, respectivamente, y . El círculo se puede representar mediante una gráfica en la vecindad de cada punto porque el lado izquierdo de su ecuación definitoria tiene un gradiente distinto de cero en cada punto del círculo. Según el teorema de la función implícita , cada subvariedad del espacio euclidiano es localmente la gráfica de una función.
Hermann Weyl dio una definición intrínseca de variedades diferenciables en su curso sobre superficies de Riemann en 1911-1912, abriendo el camino hacia el concepto general de espacio topológico que siguió poco después. Durante la década de 1930, Hassler Whitney y otros aclararon los aspectos fundamentales del tema y, por lo tanto, las intuiciones que se remontaban a la segunda mitad del siglo XIX se volvieron precisas y se desarrollaron a través de la geometría diferencial y la teoría de grupos de Lie . En particular, el teorema de incrustación de Whitney [6] mostró que la definición intrínseca en términos de gráficos era equivalente a la definición de Poincaré en términos de subconjuntos del espacio euclidiano.
Las variedades bidimensionales, también conocidas como superficies 2D incrustadas en nuestro espacio 3D común, fueron consideradas por Riemann bajo la apariencia de superficies de Riemann y clasificadas rigurosamente a principios del siglo XX por Poul Heegaard y Max Dehn . Poincaré fue pionero en el estudio de variedades tridimensionales y planteó una pregunta fundamental sobre ellas, hoy conocida como conjetura de Poincaré . Después de casi un siglo, Grigori Perelman demostró la conjetura de Poincaré (ver Solución de la conjetura de Poincaré ). El programa de geometrización de William Thurston , formulado en la década de 1970, proporcionó una extensión de gran alcance de la conjetura de Poincaré a las variedades tridimensionales generales. Las variedades de cuatro dimensiones fueron llevadas a la vanguardia de la investigación matemática en la década de 1980 por Michael Freedman y, en un entorno diferente, por Simon Donaldson , quien fue motivado por el entonces reciente progreso en la física teórica ( teoría de Yang-Mills ), donde sirven como un sustituto del espacio-tiempo 'plano' ordinario . Andrey Markov Jr. demostró en 1960 que no existe ningún algoritmo para clasificar variedades de cuatro dimensiones. René Thom , John Milnor , Stephen Smale y Sergei Novikov habían realizado anteriormente trabajos importantes sobre variedades de dimensiones superiores, incluidos análogos de la conjetura de Poincaré . Una técnica muy generalizada y flexible que subyace a gran parte del trabajo sobre la topología de variedades es la teoría de Morse .
El tipo de variedad más simple de definir es la variedad topológica, que localmente se parece a algún espacio euclidiano "ordinario" . Por definición, todas las variedades son variedades topológicas, por lo que la frase "variedad topológica" se usa generalmente para enfatizar que una variedad carece de estructura adicional, o que solo se están considerando sus propiedades topológicas. Formalmente, una variedad topológica es un espacio topológico localmente homeomorfo a un espacio euclidiano. Esto significa que cada punto tiene una vecindad para la cual existe un homeomorfismo (una función biyectiva continua cuya inversa también es continua) que asigna esa vecindad a . Estos homeomorfismos son las cartas de la variedad.
Una variedad topológica se parece localmente a un espacio euclidiano de una manera bastante débil: mientras que para cada carta individual es posible distinguir funciones diferenciables o medir distancias y ángulos, simplemente por el hecho de ser una variedad topológica un espacio no tiene ninguna característica particular y consistente. elección de tales conceptos. [7] Para discutir tales propiedades para una variedad, es necesario especificar una estructura adicional y considerar variedades diferenciables y variedades de Riemann que se analizan a continuación. En particular, la misma variedad topológica subyacente puede tener varias clases de funciones diferenciables mutuamente incompatibles y un número infinito de formas de especificar distancias y ángulos.
Generalmente se hacen suposiciones técnicas adicionales sobre el espacio topológico para excluir casos patológicos. Se acostumbra exigir que el espacio sea Hausdorff y segundo contable .
La dimensión de la variedad en un punto determinado es la dimensión del espacio euclidiano al que se asignan los gráficos en ese punto (número n en la definición). Todos los puntos en una variedad conectada tienen la misma dimensión. Algunos autores requieren que todos los gráficos de una variedad topológica se correspondan con espacios euclidianos de la misma dimensión. En ese caso, cada variedad topológica tiene un invariante topológico, su dimensión.
Para la mayoría de las aplicaciones, se utiliza un tipo especial de variedad topológica, es decir, una variedad diferenciable . Si los gráficos locales de una variedad son compatibles en cierto sentido, se pueden definir direcciones, espacios tangentes y funciones diferenciables en esa variedad. En particular, es posible utilizar cálculo en una variedad diferenciable. Cada punto de una variedad diferenciable de n dimensiones tiene un espacio tangente . Este es un espacio euclidiano de n dimensiones que consta de los vectores tangentes de las curvas que pasan por el punto.
Dos clases importantes de variedades diferenciables son las variedades suaves y analíticas . Para variedades suaves, los mapas de transición son suaves, es decir, infinitamente diferenciables. Las variedades analíticas son variedades suaves con la condición adicional de que los mapas de transición sean analíticos (se pueden expresar como series de potencias ). A la esfera se le puede dar una estructura analítica, al igual que a la mayoría de las curvas y superficies familiares.
Un conjunto rectificable generaliza la idea de una curva rectificable o suave por partes a dimensiones superiores; sin embargo, los conjuntos rectificables no son en general variedades.
Para medir distancias y ángulos en variedades, la variedad debe ser riemanniana. Una variedad de Riemann es una variedad diferenciable en la que cada espacio tangente está equipado con un producto interno de una manera que varía suavemente de un punto a otro. Dados dos vectores tangentes y , el producto interno da un número real. El producto escalar (o escalar) es un ejemplo típico de producto interno. Esto permite definir varias nociones como longitud, ángulos , áreas (o volúmenes ), curvatura y divergencia de campos vectoriales .
A todas las variedades diferenciables (de dimensión constante) se les puede dar la estructura de una variedad de Riemann. El espacio euclidiano en sí tiene una estructura natural de variedad de Riemann (los espacios tangentes se identifican naturalmente con el espacio euclidiano mismo y llevan el producto escalar estándar del espacio). Muchas curvas y superficies familiares, incluidas, por ejemplo, todas las n -esferas, se especifican como subespacios de un espacio euclidiano y heredan una métrica de su incrustación en él.
Una variedad de Finsler permite la definición de distancia pero no requiere el concepto de ángulo; es una variedad analítica en la que cada espacio tangente está equipado con una norma , , de una manera que varía suavemente de un punto a otro. Esta norma se puede extender a una métrica , definiendo la longitud de una curva; pero en general no se puede utilizar para definir un producto interno.
Cualquier variedad de Riemann es una variedad de Finsler.
Los grupos de Lie , que llevan el nombre de Sophus Lie , son variedades diferenciables que también llevan la estructura de un grupo tal que las operaciones del grupo están definidas por mapas suaves.
Un espacio vectorial euclidiano con la operación grupal de suma de vectores es un ejemplo de un grupo de Lie no compacto. Un ejemplo sencillo de un grupo de Lie compacto es el círculo: la operación del grupo es simplemente rotación. Este grupo, conocido como , también se puede caracterizar como el grupo de números complejos de módulo 1 con la multiplicación como operación grupal.
Otros ejemplos de grupos de Lie incluyen grupos especiales de matrices , que son todos subgrupos del grupo lineal general , el grupo de matrices con determinante distinto de cero. Si las entradas de la matriz son números reales , esta será una variedad desconectada de dimensiones. Los grupos ortogonales , los grupos de simetría de la esfera y las hiperesferas , son variedades dimensionales, donde es la dimensión de la esfera. Se pueden encontrar más ejemplos en la tabla de grupos de Lie .
Diferentes nociones de variedades tienen diferentes nociones de clasificación e invariante; En esta sección nos centramos en colectores cerrados y suaves.
La clasificación de variedades cerradas lisas se comprende bien en principio , excepto en la dimensión 4 : en dimensiones bajas (2 y 3) es geométrica, mediante el teorema de uniformización y la solución de la conjetura de Poincaré , y en dimensión alta (5 y superiores) es algebraico, a través de la teoría de la cirugía . Esta es una clasificación en principio: la cuestión general de si dos variedades suaves son difeomorfas no es computable en general. Además, los cálculos específicos siguen siendo difíciles y hay muchas preguntas abiertas.
Las superficies orientables se pueden visualizar y enumerar sus clases de difeomorfismo por género. Dadas dos superficies orientables, se puede determinar si son difeomorfas calculando sus respectivos géneros y comparando: son difeomorfas si y sólo si los géneros son iguales, por lo que el género forma un conjunto completo de invariantes .
Esto es mucho más difícil en dimensiones superiores: las variedades de dimensiones superiores no se pueden visualizar directamente (aunque la intuición visual es útil para comprenderlas), ni se pueden enumerar sus clases de difeomorfismo, ni se puede en general determinar si dos descripciones diferentes de una dimensión superior múltiple se refieren al mismo objeto.
Sin embargo, se puede determinar si dos variedades son diferentes si existe alguna característica intrínseca que las diferencia. Estos criterios se denominan comúnmente invariantes porque, si bien pueden definirse en términos de alguna presentación (como el género en términos de una triangulación), son los mismos en relación con todas las descripciones posibles de una variedad particular: son invariantes. bajo diferentes descripciones.
Se podría esperar desarrollar un arsenal de criterios invariantes que clasificarían definitivamente todas las variedades hasta el isomorfismo. Se sabe que para variedades de dimensión 4 y superiores, no existe ningún programa que pueda decidir si dos variedades son difeomorfas.
Las variedades suaves tienen un rico conjunto de invariantes , provenientes de la topología de conjuntos de puntos , la topología algebraica clásica y la topología geométrica . Las invariantes más familiares, que son visibles para las superficies, son la orientabilidad (una invariante normal, también detectada por homología ) y el género (una invariante homológica).
Las variedades cerradas suaves no tienen invariantes locales (aparte de la dimensión), aunque las variedades geométricas tienen invariantes locales, en particular la curvatura de una variedad de Riemann y la torsión de una variedad equipada con una conexión afín . Esta distinción entre invariantes locales y no invariantes locales es una forma común de distinguir entre geometría y topología . Por tanto, todos los invariantes de una variedad cerrada suave son globales.
La topología algebraica es una fuente de una serie de importantes propiedades invariantes globales. Algunos criterios clave incluyen la propiedad simplemente conectada y la orientabilidad (ver más abajo). De hecho, varias ramas de las matemáticas, como la teoría de la homología y la homotopía , y la teoría de clases características, se fundaron para estudiar las propiedades invariantes de las variedades.
En dimensiones dos y superiores, un criterio invariante simple pero importante es la cuestión de si una variedad admite una orientación significativa. Considere una variedad topológica con gráficos asignados a . Dada una base ordenada para , un gráfico hace que su parte de la variedad adquiera un sentido de ordenamiento, que en 3 dimensiones puede verse como diestro o zurdo. No es necesario que los gráficos superpuestos coincidan en su sentido de ordenamiento, lo que otorga a las variedades una libertad importante. Para algunas variedades, como la esfera, los gráficos se pueden elegir de modo que las regiones superpuestas coincidan en su "orientación"; estas son variedades orientables . Para otros esto es imposible. Esta última posibilidad es fácil de pasar por alto, porque cualquier superficie cerrada incrustada (sin autointersección) en un espacio tridimensional es orientable.
Algunos ejemplos ilustrativos de variedades no orientables incluyen: (1) la tira de Möbius , que es una variedad con límite, (2) la botella de Klein , que debe intersectarse a sí misma en su representación de 3 espacios, y (3) el plano proyectivo real , que surge naturalmente en la geometría.
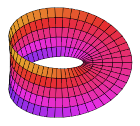
Comience con un cilindro circular infinito colocado verticalmente, una variedad sin límites. Córtalo alto y bajo para producir dos límites circulares y la franja cilíndrica entre ellos. Se trata de una variedad orientable con límite, sobre la cual se realizará la "cirugía". Corta la tira para que pueda desenrollarse y convertirse en un rectángulo, pero sujeta los extremos cortados. Gire un extremo 180°, haciendo que la superficie interior quede hacia afuera, y pegue los extremos nuevamente sin problemas. El resultado es una tira con una media torsión permanente: la tira de Möbius. Su límite ya no es un par de círculos, sino (topológicamente) un círculo único; y lo que una vez fue su "interior" se ha fusionado con su "exterior", de modo que ahora tiene un solo lado. De manera similar a la botella de Klein a continuación, esta superficie bidimensional necesitaría intersectarse en dos dimensiones, pero puede construirse fácilmente en tres o más dimensiones.
Tome dos tiras de Möbius; cada uno tiene un único bucle como límite. Endereza esos bucles formando círculos y deja que las tiras se distorsionen formando tapas cruzadas . Al pegar los círculos se producirá una nueva variedad cerrada y sin límites, la botella de Klein. Cerrar la superficie no mejora la falta de orientabilidad, simplemente elimina el límite. Así, la botella de Klein es una superficie cerrada sin distinción entre interior y exterior. En el espacio tridimensional, la superficie de una botella de Klein debe atravesarse a sí misma. Construir una botella de Klein que no se interseca requiere cuatro o más dimensiones de espacio.
Comience con una esfera centrada en el origen. Cada línea que pasa por el origen atraviesa la esfera en dos puntos opuestos llamados antípodas . Aunque no hay forma de hacerlo físicamente, es posible (considerando un espacio cociente ) fusionar matemáticamente cada par de antípodas en un solo punto. La superficie cerrada así producida es el plano proyectivo real, otra superficie más no orientable. Tiene varias descripciones y construcciones equivalentes, pero esta ruta explica su nombre: todos los puntos de cualquier línea dada que pasa por el origen se proyectan hasta el mismo "punto" en este "plano".
Para variedades bidimensionales, una propiedad invariante clave es el género , o "número de identificadores" presentes en una superficie. Un toroide es una esfera con un asa, un toro doble es una esfera con dos asas, y así sucesivamente. De hecho, es posible caracterizar completamente variedades bidimensionales compactas sobre la base del género y la orientabilidad. En variedades de dimensiones superiores, el género se reemplaza por la noción de característica de Euler y, de manera más general, los números de Betti y la homología y cohomología .
Así como existen varios tipos de variedades, existen varios tipos de mapas de variedades . Además de las funciones continuas y las funciones suaves en general, existen mapas con propiedades especiales. En topología geométrica, un tipo básico son las incrustaciones , de las cuales la teoría de nudos es un ejemplo central, y las generalizaciones como inmersiones , sumersiones , espacios de cobertura y espacios de cobertura ramificados . Los resultados básicos incluyen el teorema de incrustación de Whitney y el teorema de inmersión de Whitney .
En la geometría de Riemann, uno puede pedir mapas para preservar la métrica de Riemann, lo que lleva a nociones de incrustaciones isométricas , inmersiones isométricas e inmersiones de Riemann ; un resultado básico es el teorema de incrustación de Nash .

Un ejemplo básico de aplicaciones entre variedades son las funciones con valores escalares en una variedad,
a veces llamadas funciones regulares o funcionales , por analogía con la geometría algebraica o el álgebra lineal. Estos son de interés tanto por derecho propio como para estudiar la variedad subyacente.
En topología geométrica, las más comúnmente estudiadas son las funciones Morse , que producen descomposiciones del cuerpo del mango , mientras que en análisis matemático , a menudo se estudia la solución de ecuaciones diferenciales parciales , un ejemplo importante de lo cual es el análisis armónico , donde se estudian funciones armónicas : el núcleo de Laplace . operador . Esto conduce a funciones como los armónicos esféricos y a métodos de núcleo caliente para estudiar variedades, como escuchar la forma de un tambor y algunas pruebas del teorema del índice de Atiyah-Singer .