Superficie (matemáticas)

En matemáticas , una superficie es un modelo matemático del concepto común de superficie . Es una generalización de un plano , pero, a diferencia de este, puede ser curva ; esto es análogo a una curva que generaliza una línea recta .

Existen varias definiciones más precisas, dependiendo del contexto y de las herramientas matemáticas que se utilicen para el estudio. Las superficies matemáticas más simples son los planos y esferas en el espacio euclidiano de 3 dimensiones . La definición exacta de una superficie puede depender del contexto. Por lo general, en geometría algebraica , una superficie puede cruzarse a sí misma (y puede tener otras singularidades ), mientras que, en topología y geometría diferencial , puede que no.

Una superficie es un espacio topológico de dimensión dos; esto significa que un punto móvil sobre una superficie puede moverse en dos direcciones (tiene dos grados de libertad ). En otras palabras, alrededor de casi cada punto, hay un parche de coordenadas en el que se define un sistema de coordenadas bidimensional . Por ejemplo, la superficie de la Tierra se asemeja (idealmente) a una esfera, y la latitud y la longitud proporcionan coordenadas bidimensionales en ella (excepto en los polos y a lo largo del meridiano 180 ).

Definiciones

A menudo, una superficie se define mediante ecuaciones que se satisfacen por las coordenadas de sus puntos. Este es el caso de la gráfica de una función continua de dos variables. El conjunto de los ceros de una función de tres variables es una superficie, que se denomina superficie implícita . ^[1] Si la función de tres variables que la define es un polinomio , la superficie es una superficie algebraica . Por ejemplo, la esfera unitaria es una superficie algebraica, ya que puede definirse mediante la ecuación implícita

x^{2}+y^{2}+z^{2}-1=0.

Una superficie también puede definirse como la imagen , en algún espacio de dimensión al menos 3, de una función continua de dos variables (se requieren algunas condiciones adicionales para garantizar que la imagen no sea una curva ). En este caso, se dice que se tiene una superficie paramétrica , que está parametrizada por estas dos variables, llamadas parámetros . Por ejemplo, la esfera unitaria puede estar parametrizada por los ángulos de Euler , también llamados longitud $u$ y latitud $v$ por

{\begin{aligned}x&=\cos(u)\cos(v)\\y&=\sin(u)\cos(v)\\z&=\sin(v)\,.\end{aligned}}

Las ecuaciones paramétricas de superficies suelen ser irregulares en algunos puntos. Por ejemplo, todos los puntos de la esfera unitaria, excepto dos, son la imagen, por la parametrización anterior, de exactamente un par de ángulos de Euler ( módulo $2 π$ ). Para los dos puntos restantes (los polos norte y sur ), se tiene $cos v = 0$ y la longitud $u$ puede tomar cualquier valor. Además, hay superficies para las que no puede existir una única parametrización que cubra toda la superficie. Por lo tanto, a menudo se consideran superficies que están parametrizadas por varias ecuaciones paramétricas, cuyas imágenes cubren la superficie. Esto se formaliza mediante el concepto de variedad : en el contexto de las variedades, típicamente en topología y geometría diferencial , una superficie es una variedad de dimensión dos; esto significa que una superficie es un espacio topológico tal que cada punto tiene un entorno que es homeomorfo a un subconjunto abierto del plano euclidiano (véase Superficie (topología) y Superficie (geometría diferencial) ). Esto permite definir superficies en espacios de dimensión superior a tres, e incluso superficies abstractas , que no están contenidas en ningún otro espacio. Por otro lado, esto excluye superficies que tienen singularidades , como el vértice de una superficie cónica o los puntos donde una superficie se cruza consigo misma.

En geometría clásica , una superficie se define generalmente como el lugar geométrico de un punto o una línea. Por ejemplo, una esfera es el lugar geométrico de un punto que se encuentra a una distancia dada de un punto fijo, llamado centro; una superficie cónica es el lugar geométrico de una línea que pasa por un punto fijo y cruza una curva ; una superficie de revolución es el lugar geométrico de una curva que gira alrededor de una línea. Una superficie reglada es el lugar geométrico de una línea en movimiento que satisface ciertas restricciones; en la terminología moderna, una superficie reglada es una superficie que es una unión de líneas.

Terminología

Existen varios tipos de superficies que se consideran en matemáticas. Por lo tanto, es necesaria una terminología unívoca para distinguirlas cuando sea necesario. Una superficie topológica es una superficie que es una variedad de dimensión dos (véase § Superficie topológica). Una superficie diferenciable es una superficie que es una variedad diferenciable (véase § Superficie diferenciable). Toda superficie diferenciable es una superficie topológica, pero la recíproca es falsa.

A menudo se supone implícitamente que una "superficie" está contenida en un espacio euclidiano de dimensión 3, normalmente $R 3$ . Una superficie que está contenida en un espacio proyectivo se denomina superficie proyectiva (véase § Superficie proyectiva). Una superficie que no se supone que esté incluida en otro espacio se denomina superficie abstracta .

Ejemplos

La gráfica de una función continua de dos variables, definida sobre un subconjunto abierto conexo de $R$ $2$ es una superficie topológica . Si la función es diferenciable , la gráfica es una superficie diferenciable .
Un plano es a la vez una superficie algebraica y una superficie diferenciable. También es una superficie reglada y una superficie de revolución .
Un cilindro circular (es decir, el lugar geométrico de una línea que cruza un círculo y es paralela a una dirección dada) es una superficie algebraica y una superficie diferenciable.
Un cono circular (lugar geométrico de una línea que corta un círculo y pasa por un punto fijo, el vértice , que está fuera del plano del círculo) es una superficie algebraica que no es una superficie diferenciable. Si se elimina el vértice, el resto del cono es la unión de dos superficies diferenciables.
La superficie de un poliedro es una superficie topológica, que no es una superficie diferenciable ni una superficie algebraica.
Un paraboloide hiperbólico (la gráfica de la función $z = xy$ ) es una superficie diferenciable y una superficie algebraica. También es una superficie reglada y, por este motivo, se utiliza a menudo en arquitectura .
Un hiperboloide de dos hojas es una superficie algebraica y la unión de dos superficies diferenciables que no se intersecan.

Superficie paramétrica

Una superficie paramétrica es la imagen de un subconjunto abierto del plano euclidiano (normalmente ) por una función continua , en un espacio topológico , generalmente un espacio euclidiano de dimensión al menos tres. Habitualmente se supone que la función es continuamente diferenciable , y este será siempre el caso en este artículo. $\mathbb {R} ^{2}$

En concreto, una superficie paramétrica en está dada por tres funciones de dos variables $u$ y $v$ , llamadas parámetros $\mathbb {R} ^{3}$

{\begin{aligned}x&=f_{1}(u,v),\\[4pt]y&=f_{2}(u,v),\\[4pt]z&=f_{3}(u,v)\,.\end{aligned}}

Como la imagen de dicha función puede ser una curva (por ejemplo, si las tres funciones son constantes con respecto a $v$ ), se requiere una condición adicional, generalmente que, para casi todos los valores de los parámetros, la matriz jacobiana

{\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial u}}&{\dfrac {\partial f_{1}}{\partial v}}\\[6pt]{\dfrac {\partial f_{2}}{\partial u}}&{\dfrac {\partial f_{2}}{\partial v}}\\[6pt]{\dfrac {\partial f_{3}}{\partial u}}&{\dfrac {\partial f_{3}}{\partial v}}\end{bmatrix}}

tiene rango dos. Aquí "casi todos" significa que los valores de los parámetros donde el rango es dos contienen un subconjunto denso y abierto del rango de la parametrización. Para superficies en un espacio de mayor dimensión, la condición es la misma, excepto por el número de columnas de la matriz jacobiana.

Plano tangente y vector normal

Un punto $p$ donde la matriz jacobiana anterior tiene rango dos se llama regular o, más apropiadamente, la parametrización se llama regular en $p$ .

El plano tangente en un punto regular $p$ es el único plano que pasa por $p$ y que tiene una dirección paralela a los dos vectores fila de la matriz jacobiana. El plano tangente es un concepto afín , porque su definición es independiente de la elección de una métrica . En otras palabras, cualquier transformación afín asigna el plano tangente a la superficie en un punto al plano tangente a la imagen de la superficie en la imagen del punto.

La línea normal en un punto de una superficie es la única línea que pasa por el punto y es perpendicular al plano tangente; el vector normal es un vector que es paralelo a la normal.

Para otros invariantes diferenciales de superficies, en la vecindad de un punto, véase Geometría diferencial de superficies .

Punto irregular y punto singular

Un punto de una superficie paramétrica que no es regular es irregular . Existen varios tipos de puntos irregulares.

Puede ocurrir que un punto irregular se vuelva regular si se cambia la parametrización. Es el caso de los polos en la parametrización de la esfera unidad por los ángulos de Euler : basta con permutar el papel de los diferentes ejes de coordenadas para cambiar los polos.

Por otra parte, consideremos el cono circular de ecuación paramétrica

{\begin{aligned}x&=t\cos(u)\\y&=t\sin(u)\\z&=t\,.\end{aligned}}

El vértice del cono es el origen $(0, 0, 0)$ , y se obtiene para $t = 0$ . Es un punto irregular que permanece irregular, cualquiera que sea la parametrización elegida (de lo contrario, existiría un único plano tangente). Un punto irregular de este tipo, donde el plano tangente no está definido, se dice singular .

Existe otro tipo de puntos singulares. Son los puntos de autocruce , es decir, los puntos en los que la superficie se cruza consigo misma. En otras palabras, son los puntos que se obtienen para (al menos) dos valores distintos de los parámetros.

Gráfica de una función bivariada

Sea $z = f (x, y)$ una función de dos variables reales. Esta es una superficie paramétrica, parametrizada como

{\begin{aligned}x&=t\\y&=u\\z&=f(t,u)\,.\end{aligned}}

Cada punto de esta superficie es regular, ya que las dos primeras columnas de la matriz jacobiana forman la matriz identidad de rango dos.

Superficie racional

Una superficie racional es una superficie que puede ser parametrizada por funciones racionales de dos variables. Es decir, si $f i (t, u)$ son, para $i = 0, 1, 2, 3$ , polinomios en dos indeterminados, entonces la superficie paramétrica, definida por

{\begin{aligned}x&={\frac {f_{1}(t,u)}{f_{0}(t,u)}},\\[6pt]y&={\frac {f_{2}(t,u)}{f_{0}(t,u)}},\\[6pt]z&={\frac {f_{3}(t,u)}{f_{0}(t,u)}}\,,\end{aligned}}

es una superficie racional.

Una superficie racional es una superficie algebraica , pero la mayoría de las superficies algebraicas no son racionales.

Superficie implícita

Una superficie implícita en un espacio euclidiano (o, más generalmente, en un espacio afín ) de dimensión 3 es el conjunto de los ceros comunes de una función diferenciable de tres variables.

f(x,y,z)=0.

Implícito significa que la ecuación define implícitamente una de las variables como función de las otras variables. Esto se hace más exacto mediante el teorema de la función implícita : si $f (x 0, y 0, z 0) = 0$ , y la derivada parcial en $z$ de $f$ no es cero en $(x 0, y 0, z 0)$ , entonces existe una función diferenciable $φ (x, y)$ tal que

f(x,y,\varphi (x,y))=0

en un entorno de $(x 0, y 0, z 0)$ . En otras palabras, la superficie implícita es el gráfico de una función cerca de un punto de la superficie donde la derivada parcial en $z$ es distinta de cero. Una superficie implícita tiene, por tanto, localmente, una representación paramétrica, excepto en los puntos de la superficie donde las tres derivadas parciales son cero.

Puntos regulares y plano tangente

Un punto de la superficie donde al menos una derivada parcial de $f$ es distinta de cero se llama regular . En tal punto , el plano tangente y la dirección de la normal están bien definidos, y pueden deducirse, con el teorema de la función implícita de la definición dada anteriormente, en § Plano tangente y vector normal . La dirección de la normal es el gradiente , es decir, el vector $(x_{0},y_{0},z_{0})$

\left[{\frac {\partial f}{\partial x}}(x_{0},y_{0},z_{0}),{\frac {\partial f}{\partial y}}(x_{0},y_{0},z_{0}),{\frac {\partial f}{\partial z}}(x_{0},y_{0},z_{0})\right].

El plano tangente se define por su ecuación implícita

{\frac {\partial f}{\partial x}}(x_{0},y_{0},z_{0})(x-x_{0})+{\frac {\partial f}{\partial y}}(x_{0},y_{0},z_{0})(y-y_{0})+{\frac {\partial f}{\partial z}}(x_{0},y_{0},z_{0})(z-z_{0})=0.

Punto singular

Un punto singular de una superficie implícita (en ) es un punto de la superficie donde se cumple la ecuación implícita y las tres derivadas parciales de su función definitoria son todas cero. Por lo tanto, los puntos singulares son las soluciones de un sistema de cuatro ecuaciones en tres indeterminadas. Como la mayoría de estos sistemas no tienen solución, muchas superficies no tienen ningún punto singular. Una superficie sin ningún punto singular se llama regular o no singular . $\mathbb {R} ^{3}$

El estudio de las superficies cerca de sus puntos singulares y la clasificación de estos puntos singulares es la teoría de la singularidad . Un punto singular está aislado si no hay otro punto singular en sus proximidades. De lo contrario, los puntos singulares pueden formar una curva. Este es en particular el caso de las superficies que se cruzan entre sí.

Superficie algebraica

Originalmente, una superficie algebraica era una superficie que podía definirse mediante una ecuación implícita

f(x,y,z)=0,

donde $f$ es un polinomio en tres indeterminados , con coeficientes reales.

El concepto se ha ampliado en varias direcciones, definiendo superficies sobre cuerpos arbitrarios y considerando superficies en espacios de dimensión arbitraria o en espacios proyectivos . También se consideran superficies algebraicas abstractas, que no están explícitamente insertas en otro espacio.

Superficies sobre campos arbitrarios

Los polinomios con coeficientes en cualquier campo se aceptan para definir una superficie algebraica. Sin embargo, el campo de coeficientes de un polinomio no está bien definido, ya que, por ejemplo, un polinomio con coeficientes racionales también puede considerarse como un polinomio con coeficientes reales o complejos . Por lo tanto, el concepto de punto de la superficie se ha generalizado de la siguiente manera. ^[2]^{[ página necesaria ]}

Dado un polinomio $f (x, y, z)$ , sea $k$ el cuerpo más pequeño que contiene los coeficientes, y $K$ una extensión algebraicamente cerrada de $k$ , de grado de trascendencia infinito . ^[3] Entonces un punto de la superficie es un elemento de $K 3$ que es una solución de la ecuación

f(x,y,z)=0.

Si el polinomio tiene coeficientes reales, el cuerpo $K$ es el cuerpo complejo , y un punto de la superficie que pertenece a (un punto usual) se llama punto real . Un punto que pertenece a $k$ $3$ se llama racional sobre $k$ , o simplemente un punto racional , si $k$ es el cuerpo de números racionales . $\mathbb {R} ^{3}$

Superficie proyectiva

Una superficie proyectiva en un espacio proyectivo de dimensión tres es el conjunto de puntos cuyas coordenadas homogéneas son ceros de un único polinomio homogéneo de cuatro variables. En términos más generales, una superficie proyectiva es un subconjunto de un espacio proyectivo, que es una variedad proyectiva de dimensión dos.

Las superficies proyectivas están fuertemente relacionadas con las superficies afines (es decir, las superficies algebraicas ordinarias). Se pasa de una superficie proyectiva a la superficie afín correspondiente fijando en una de ellas alguna coordenada o indeterminación de los polinomios definitorios (normalmente el último). A la inversa, se pasa de una superficie afín a su superficie proyectiva asociada (llamada completitud proyectiva ) homogeneizando el polinomio definitorio (en el caso de superficies en un espacio de dimensión tres), o homogeneizando todos los polinomios del ideal definitorio (para superficies en un espacio de dimensión superior).

En espacios de dimensiones superiores

No se puede definir el concepto de superficie algebraica en un espacio de dimensión superior a tres sin una definición general de variedad algebraica y de la dimensión de una variedad algebraica . De hecho, una superficie algebraica es una variedad algebraica de dimensión dos .

Más precisamente, una superficie algebraica en un espacio de dimensión $n$ es el conjunto de los ceros comunes de al menos $n - 2$ polinomios, pero estos polinomios deben satisfacer otras condiciones que pueden no ser inmediatas de verificar. En primer lugar, los polinomios no deben definir una variedad o un conjunto algebraico de mayor dimensión, lo que suele ser el caso si uno de los polinomios está en el ideal generado por los otros. Generalmente, $n - 2$ polinomios definen un conjunto algebraico de dimensión dos o superior. Si la dimensión es dos, el conjunto algebraico puede tener varios componentes irreducibles . Si solo hay un componente, los $n - 2$ polinomios definen una superficie, que es una intersección completa . Si hay varios componentes, entonces se necesitan más polinomios para seleccionar un componente específico.

La mayoría de los autores consideran como superficies algebraicas sólo las variedades algebraicas de dimensión dos, pero algunos también consideran como superficies todos los conjuntos algebraicos cuyos componentes irreducibles tienen dimensión dos.

En el caso de superficies en un espacio de dimensión tres, toda superficie es una intersección completa, y una superficie está definida por un único polinomio, que es irreducible o no, dependiendo de si los conjuntos algebraicos no irreducibles de dimensión dos se consideran superficies o no.

Superficie topológica

En topología , una superficie se define generalmente como una variedad de dimensión dos. Esto significa que una superficie topológica es un espacio topológico tal que cada punto tiene un entorno que es homeomorfo a un subconjunto abierto de un plano euclidiano .

Toda superficie topológica es homeomorfa a una superficie poliédrica tal que todas sus facetas son triángulos . El estudio combinatorio de tales disposiciones de triángulos (o, más generalmente, de símplex de dimensiones superiores ) es el objeto de partida de la topología algebraica . Esto permite la caracterización de las propiedades de las superficies en términos de invariantes puramente algebraicos , como los grupos de género y homología .

Las clases de homeomorfismo de superficies se han descrito completamente (ver Superficie (topología) ).

Superficie diferenciable

En matemáticas , la geometría diferencial de superficies se ocupa de la geometría diferencial de superficies lisas ^[a] con varias estructuras adicionales, más frecuentemente, una métrica de Riemann . ^[b]

Las superficies han sido ampliamente estudiadas desde varias perspectivas: extrínsecamente , en relación con su inserción en el espacio euclidiano e intrínsecamente , reflejando sus propiedades determinadas únicamente por la distancia dentro de la superficie medida a lo largo de las curvas de la superficie. Uno de los conceptos fundamentales investigados es la curvatura gaussiana , estudiada en profundidad por primera vez por Carl Friedrich Gauss , ^[4] quien demostró que la curvatura era una propiedad intrínseca de una superficie, independiente de su inserción isométrica en el espacio euclidiano.

Las superficies surgen naturalmente como gráficos de funciones de un par de variables , y a veces aparecen en forma paramétrica o como lugares geométricos asociados a curvas espaciales . Un papel importante en su estudio lo han desempeñado los grupos de Lie (en el espíritu del programa de Erlangen ), a saber, los grupos de simetría del plano euclidiano , la esfera y el plano hiperbólico . Estos grupos de Lie se pueden utilizar para describir superficies de curvatura gaussiana constante; también proporcionan un ingrediente esencial en el enfoque moderno de la geometría diferencial intrínseca a través de conexiones . Por otro lado, las propiedades extrínsecas que dependen de una incrustación de una superficie en el espacio euclidiano también se han estudiado ampliamente. Esto está bien ilustrado por las ecuaciones no lineales de Euler-Lagrange en el cálculo de variaciones : aunque Euler desarrolló las ecuaciones de una variable para comprender las geodésicas , definidas independientemente de una incrustación, una de las principales aplicaciones de Lagrange de las ecuaciones de dos variables fue a las superficies mínimas , un concepto que solo se puede definir en términos de una incrustación.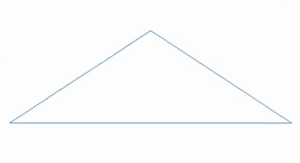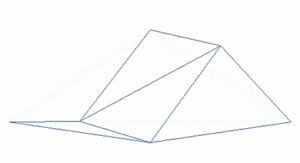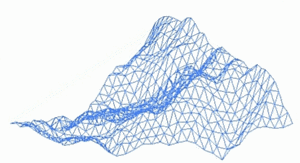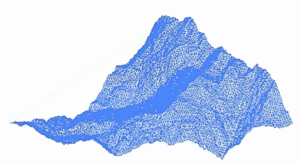

Superficie fractal

Un paisaje fractal o superficie fractal se genera utilizando un algoritmo estocástico diseñado para producir un comportamiento fractal que imita la apariencia del terreno natural . En otras palabras, la superficie resultante del procedimiento no es determinista, sino más bien una superficie aleatoria que exhibe un comportamiento fractal. ^[5]

Muchos fenómenos naturales presentan alguna forma de autosimilitud estadística que puede ser modelada por superficies fractales . ^[6] Además, las variaciones en la textura de la superficie proporcionan importantes pistas visuales sobre la orientación y las pendientes de las superficies, y el uso de patrones fractales casi autosimilares puede ayudar a crear efectos visuales de apariencia natural. ^[7] El modelado de las superficies rugosas de la Tierra a través del movimiento browniano fraccional fue propuesto por primera vez por Benoit Mandelbrot . ^[8]

Dado que el resultado previsto del proceso es producir un paisaje, en lugar de una función matemática, con frecuencia se aplican a dichos paisajes procesos que pueden afectar la estacionariedad e incluso el comportamiento fractal general de dicha superficie , con el fin de producir un paisaje más convincente.

Según RR Shearer , la generación de superficies y paisajes de aspecto natural fue un punto de inflexión importante en la historia del arte, donde la distinción entre imágenes geométricas generadas por computadora y arte natural hecho por el hombre se volvió borrosa. ^[9] El primer uso de un paisaje generado por fractales en una película fue en 1982 para la película Star Trek II: La ira de Khan . Loren Carpenter refinó las técnicas de Mandelbrot para crear un paisaje alienígena. ^[10]

En gráficos por computadora

En las aplicaciones técnicas de gráficos por computadora en 3D ( CAx ), como el diseño asistido por computadora y la fabricación asistida por computadora , las superficies son una forma de representar objetos. Las otras formas son los wireframes (líneas y curvas) y los sólidos. Las nubes de puntos también se utilizan a veces como formas temporales de representar un objeto, con el objetivo de utilizar los puntos para crear una o más de las tres representaciones permanentes.

Véase también

Elemento de área , el área de un elemento diferencial de una superficie.
Superficies de coordenadas
Hipersuperficie
Perímetro , un equivalente bidimensional
Superficie poliédrica
Forma
Función de distancia con signo
Figura sólida
Área de superficie
Parche de superficie
Integral de superficie

Notas al pie

^ Una superficie lisa es una superficie en la que cada punto tiene una vecindad difeomorfa a algún conjunto abierto en E ² .
^ Una superficie de Riemann es una superficie lisa equipada con una métrica de Riemann.

Notas

^ Aquí, "implícito" no se refiere a una propiedad de la superficie que puede definirse por otros medios, sino a cómo se define. Por lo tanto, este término es una abreviatura de "superficie definida por una ecuación implícita ".
^ Weil, André (1946), Fundamentos de geometría algebraica, Publicaciones del Colloquium de la American Mathematical Society, vol. 29, Providence, RI: American Mathematical Society , págs. 1–363, ISBN 9780821874622, Sr. 0023093^{[ página necesaria ]}
^ El grado infinito de trascendencia es una condición técnica que permite definir con precisión el concepto de punto genérico .
^ Gauss 1902.
^ "La geometría fractal de la naturaleza".
^ Avances en modelado multimedia: 13.° Congreso Internacional de Modelado Multimedia por Tat-Jen Cham 2007 ISBN 3-540-69428-5 página [1]
^ Percepción de la simetría humana y su análisis computacional por Christopher W. Tyler 2002 ISBN 0-8058-4395-7 páginas 173–177 [2]
^ Dinámica de superficies fractales por la familia Fereydoon y Tamas Vicsek 1991 ISBN 981-02-0720-4 página 45 [3]
^ Rhonda Roland Shearer "Repensando imágenes y metáforas" en Los lenguajes del cerebro de Albert M. Galaburda 2002 ISBN 0-674-00772-7 páginas 351–359 [4]
^ Briggs, John (1992). Fractales: los patrones del caos: una nueva estética del arte, la ciencia y la naturaleza. Simon and Schuster. pág. 84. ISBN 978-0671742171. Recuperado el 15 de junio de 2014 .

Fuentes

Gauss, Carl Friedrich (1902), Investigaciones generales sobre superficies curvas de 1825 y 1827, Biblioteca de la Universidad de Princeton