stringtranslate.com

Química computacional

Complejo metálico de dicromo con un campo electrostático a su alrededor. Modelado con WebMO. [1]

La química computacional es una rama de la química que utiliza simulaciones por computadora para ayudar a resolver problemas químicos. [2] Utiliza métodos de química teórica incorporados en programas informáticos para calcular las estructuras y propiedades de moléculas , grupos de moléculas y sólidos. [3] La importancia de este tema se debe al hecho de que, con la excepción de algunos hallazgos relativamente recientes relacionados con el ion molecular de hidrógeno ( catión dihidrógeno ), no es factible lograr una representación mecánica cuántica precisa de los sistemas químicos de forma analítica o en forma cerrada. [4] La complejidad inherente al problema de muchos cuerpos exacerba el desafío de proporcionar descripciones detalladas de los sistemas mecánicos cuánticos. [5] Si bien los resultados computacionales normalmente complementan la información obtenida por experimentos químicos , ocasionalmente pueden predecir fenómenos químicos no observados . [6]

Descripción general

La química computacional se diferencia de la química teórica , que implica una descripción matemática de la química. Sin embargo, la química computacional implica el uso de programas informáticos y habilidades matemáticas adicionales para modelar con precisión varios problemas químicos. En la química teórica, los químicos, físicos y matemáticos desarrollan algoritmos y programas informáticos para predecir propiedades atómicas y moleculares y vías de reacción para reacciones químicas. Los químicos computacionales, por el contrario, pueden simplemente aplicar programas informáticos y metodologías existentes a cuestiones químicas específicas. [7]

Históricamente, la química computacional ha tenido dos vertientes diferentes:

Estos aspectos, junto con el propósito de la química computacional, han dado lugar a toda una serie de algoritmos.

Historia

Basándose en los descubrimientos y teorías fundacionales en la historia de la mecánica cuántica , los primeros cálculos teóricos en química fueron los de Walter Heitler y Fritz London en 1927, utilizando la teoría del enlace de valencia . [9] Los libros que fueron influyentes en el desarrollo temprano de la química cuántica computacional incluyen Introducción a la mecánica cuántica de Linus Pauling y E. Bright Wilson de 1935 , con aplicaciones a la química , [10] Química cuántica de Eyring , Walter y Kimball de 1944 , [11] Mecánica de ondas elemental de Heitler de 1945 , con aplicaciones a la química cuántica , [12] y más tarde el libro de texto de Coulson de 1952, Valence , cada uno de los cuales sirvió como referencias principales para los químicos en las décadas siguientes. [13]

Con el desarrollo de la tecnología informática eficiente en la década de 1940, las soluciones de ecuaciones de onda elaboradas para sistemas atómicos complejos comenzaron a ser un objetivo realizable. A principios de la década de 1950, se realizaron los primeros cálculos orbitales atómicos semiempíricos. Los químicos teóricos se convirtieron en usuarios extensivos de las primeras computadoras digitales. Un avance significativo fue marcado por el artículo de Clemens CJ Roothaan de 1951 en Reviews of Modern Physics. [14] [15] Este artículo se centró principalmente en el enfoque "LCAO MO" (combinación lineal de orbitales atómicos y orbitales moleculares). Durante muchos años, fue el segundo artículo más citado en esa revista. [14] [15] Smith y Sutcliffe ofrecen una descripción muy detallada de dicho uso en el Reino Unido. [16] Los primeros cálculos ab initio del método Hartree-Fock sobre moléculas diatómicas se realizaron en 1956 en el MIT, utilizando un conjunto base de orbitales de Slater . [17] Para las moléculas diatómicas, un estudio sistemático utilizando un conjunto base mínimo y el primer cálculo con un conjunto base más grande fueron publicados por Ransil y Nesbet respectivamente en 1960. [18] Los primeros cálculos poliatómicos utilizando orbitales gaussianos se realizaron a finales de la década de 1950. Los primeros cálculos de interacción de configuración se realizaron en Cambridge en la computadora EDSAC en la década de 1950 utilizando orbitales gaussianos por Boys y colaboradores. [19] Para 1971, cuando se publicó una bibliografía de cálculos ab initio , [20] las moléculas más grandes incluidas eran naftaleno y azuleno . [21] [22] Schaefer ha publicado resúmenes de muchos desarrollos anteriores en la teoría ab initio . [23]

En 1964, los cálculos del método Hückel (utilizando un método de combinación lineal simple de orbitales atómicos (LCAO) para determinar las energías electrónicas de los orbitales moleculares de los electrones π en sistemas de hidrocarburos conjugados) de moléculas, que varían en complejidad desde butadieno y benceno hasta ovaleno , se generaron en computadoras en Berkeley y Oxford. [24] Estos métodos empíricos fueron reemplazados en la década de 1960 por métodos semiempíricos como CNDO . [25]

A principios de la década de 1970, comenzaron a usarse programas informáticos eficientes ab initio como ATMOL, Gaussian , IBMOL y POLYAYTOM, para acelerar los cálculos ab initio de orbitales moleculares. [26] De estos cuatro programas, solo Gaussian, ahora ampliamente expandido, todavía está en uso, pero muchos otros programas ahora están en uso. [26] Al mismo tiempo, los métodos de mecánica molecular , como el campo de fuerza MM2 , fueron desarrollados, principalmente por Norman Allinger . [27]

Una de las primeras menciones del término química computacional se puede encontrar en el libro Computers and Their Role in the Physical Sciences de Sidney Fernbach y Abraham Haskell Taub, de 1970, donde afirman: "Parece, por tanto, que la 'química computacional' puede finalmente ser cada vez más una realidad". [28] Durante la década de 1970, se empezaron a considerar métodos muy diferentes como parte de una nueva disciplina emergente de la química computacional . [29] El Journal of Computational Chemistry se publicó por primera vez en 1980.

La química computacional ha aparecido en varios premios Nobel, más notablemente en 1998 y 2013. Walter Kohn , "por su desarrollo de la teoría funcional de la densidad", y John Pople , "por su desarrollo de métodos computacionales en química cuántica", recibieron el Premio Nobel de Química de 1998. [30] Martin Karplus , Michael Levitt y Arieh Warshel recibieron el Premio Nobel de Química de 2013 por "el desarrollo de modelos multiescala para sistemas químicos complejos". [31]

Aplicaciones

Hay varios campos dentro de la química computacional.

Estos campos pueden dar lugar a varias aplicaciones como se muestra a continuación.

Catálisis

La química computacional puede ayudar a predecir valores como la energía de activación de la catálisis. La presencia del catalizador abre una vía de reacción diferente (mostrada en rojo) con menor energía de activación. El resultado final y la termodinámica general son los mismos.

La química computacional es una herramienta para analizar sistemas catalíticos sin hacer experimentos. La teoría de la estructura electrónica moderna y la teoría funcional de la densidad han permitido a los investigadores descubrir y comprender los catalizadores . [37] Los estudios computacionales aplican la química teórica a la investigación de la catálisis. Los métodos de la teoría funcional de la densidad calculan las energías y los orbitales de las moléculas para dar modelos de esas estructuras. [38] Usando estos métodos, los investigadores pueden predecir valores como la energía de activación , la reactividad del sitio [39] y otras propiedades termodinámicas. [38]

Los datos que son difíciles de obtener experimentalmente se pueden encontrar utilizando métodos computacionales para modelar los mecanismos de los ciclos catalíticos. [39] Los químicos computacionales expertos proporcionan predicciones que se acercan a los datos experimentales con consideraciones adecuadas de métodos y conjuntos de bases. Con buenos datos computacionales, los investigadores pueden predecir cómo se pueden mejorar los catalizadores para reducir el costo y aumentar la eficiencia de estas reacciones. [38]

Desarrollo de fármacos

La química computacional se utiliza en el desarrollo de fármacos para modelar moléculas de fármacos potencialmente útiles y ayudar a las empresas a ahorrar tiempo y dinero en el desarrollo de fármacos. El proceso de descubrimiento de fármacos implica analizar datos, encontrar formas de mejorar las moléculas actuales, encontrar rutas sintéticas y probar esas moléculas. [36] La química computacional ayuda con este proceso al proporcionar predicciones de qué experimentos sería mejor hacer sin realizar otros experimentos. Los métodos computacionales también pueden encontrar valores que son difíciles de encontrar experimentalmente, como los pKa de los compuestos. [40] Los métodos como la teoría funcional de la densidad se pueden utilizar para modelar moléculas de fármacos y encontrar sus propiedades, como sus energías HOMO y LUMO y orbitales moleculares. Los químicos computacionales también ayudan a las empresas con el desarrollo de la informática, la infraestructura y los diseños de fármacos. [41]

Además de la síntesis de fármacos, los químicos computacionales también investigan los portadores de fármacos para nanomateriales . Esto permite a los investigadores simular entornos para probar la eficacia y la estabilidad de los portadores de fármacos. Comprender cómo interactúa el agua con estos nanomateriales garantiza la estabilidad del material en los cuerpos humanos. Estas simulaciones computacionales ayudan a los investigadores a optimizar el material y encontrar la mejor manera de estructurar estos nanomateriales antes de fabricarlos. [42]

Bases de datos de química computacional

Las bases de datos son útiles tanto para los químicos computacionales como para los no computacionales en la investigación y para verificar la validez de los métodos computacionales. Los datos empíricos se utilizan para analizar el error de los métodos computacionales en comparación con los datos experimentales. Los datos empíricos ayudan a los investigadores con sus métodos y conjuntos de bases para tener una mayor confianza en los resultados de los investigadores. Las bases de datos de química computacional también se utilizan para probar software o hardware para química computacional. [43]

Las bases de datos también pueden utilizar datos puramente calculados. Los datos puramente calculados utilizan valores calculados en lugar de valores experimentales para las bases de datos. Los datos puramente calculados evitan tener que lidiar con estos ajustes para diferentes condiciones experimentales, como la energía del punto cero. Estos cálculos también pueden evitar errores experimentales en el caso de moléculas difíciles de probar. Aunque los datos puramente calculados a menudo no son perfectos, identificar problemas suele ser más fácil para los datos calculados que para los experimentales. [43]

Las bases de datos también brindan acceso público a la información para que la utilicen los investigadores. Contienen datos que otros investigadores han encontrado y cargado en estas bases de datos para que cualquiera pueda buscarlos. Los investigadores utilizan estas bases de datos para encontrar información sobre moléculas de interés y aprender qué se puede hacer con ellas. Algunas bases de datos de química disponibles públicamente incluyen las siguientes. [43]

Métodos

Desde el principiométodo

Los programas utilizados en química computacional se basan en muchos métodos químicos cuánticos diferentes que resuelven la ecuación molecular de Schrödinger asociada con el hamiltoniano molecular . [46] Los métodos que no incluyen ningún parámetro empírico o semiempírico en sus ecuaciones (derivados directamente de la teoría, sin incluir datos experimentales) se denominan métodos ab initio . [47] Una aproximación teórica se define rigurosamente en primeros principios y luego se resuelve dentro de un margen de error que se conoce cualitativamente de antemano. Si se deben utilizar métodos iterativos numéricos, el objetivo es iterar hasta obtener la precisión total de la máquina (lo mejor que sea posible con una longitud de palabra finita en la computadora y dentro de las aproximaciones matemáticas y/o físicas realizadas). [48]

Los métodos ab initio necesitan definir un nivel de teoría (el método) y un conjunto de bases. [49] Un conjunto de bases consiste en funciones centradas en los átomos de la molécula. Estos conjuntos se utilizan luego para describir orbitales moleculares a través del método de orbitales moleculares de combinación lineal de orbitales atómicos (LCAO) . [50]

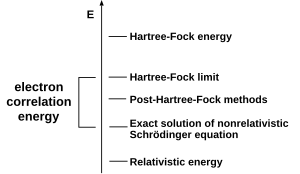
Diagrama que ilustra diversos métodos de estructura electrónica ab initio en términos de energía. Los espaciamientos no están a escala.

Un tipo común de cálculo de la estructura electrónica ab initio es el método Hartree-Fock (HF), una extensión de la teoría de orbitales moleculares , donde las repulsiones electrón-electrón en la molécula no se tienen en cuenta específicamente; solo se incluye en el cálculo el efecto promedio de los electrones. A medida que aumenta el tamaño del conjunto base, la energía y la función de onda tienden hacia un límite llamado límite Hartree-Fock. [50]

Muchos tipos de cálculos comienzan con un cálculo Hartree-Fock y posteriormente corrigen la repulsión electrón-electrón, también denominada correlación electrónica . [51] Estos tipos de cálculos se denominan métodos post-Hartree-Fock . Al mejorar continuamente estos métodos, los científicos pueden acercarse cada vez más a la predicción perfecta del comportamiento de los sistemas atómicos y moleculares en el marco de la mecánica cuántica, tal como se define en la ecuación de Schrödinger. [52] Para obtener una concordancia exacta con el experimento, es necesario incluir términos específicos, algunos de los cuales son mucho más importantes para los átomos pesados ​​que para los más ligeros. [53]

En la mayoría de los casos, la función de onda de Hartree-Fock ocupa una única configuración o determinante. [54] En algunos casos, en particular para los procesos de ruptura de enlaces, esto es inadecuado y se deben utilizar varias configuraciones . [55]

La energía molecular total puede evaluarse como una función de la geometría molecular ; en otras palabras, la superficie de energía potencial . [56] Una superficie de este tipo puede utilizarse para la dinámica de la reacción. Los puntos estacionarios de la superficie conducen a predicciones de diferentes isómeros y las estructuras de transición para la conversión entre isómeros, pero estas pueden determinarse sin un conocimiento completo de la superficie completa. [53]

Diagrama de orbitales moleculares de los sistemas pi conjugados de la molécula de diazometano utilizando el método de Hartree-Fock, CH 2 N 2

Termoquímica computacional

Un objetivo particularmente importante, llamado termoquímica computacional , es calcular magnitudes termoquímicas como la entalpía de formación con precisión química. La precisión química es la precisión requerida para hacer predicciones químicas realistas y generalmente se considera que es de 1 kcal/mol o 4 kJ/mol. Para alcanzar esa precisión de manera económica, es necesario utilizar una serie de métodos post-Hartree-Fock y combinar los resultados. Estos métodos se denominan métodos compuestos de química cuántica . [57]

Dinámica química

Después de que las variables electrónicas y nucleares se separan dentro de la representación de Born-Oppenheimer), el paquete de ondas correspondiente a los grados de libertad nucleares se propaga a través del operador de evolución temporal (física) asociado a la ecuación de Schrödinger dependiente del tiempo (para el hamiltoniano molecular completo ). [58] En el enfoque complementario dependiente de la energía, la ecuación de Schrödinger independiente del tiempo se resuelve utilizando el formalismo de la teoría de dispersión . El potencial que representa la interacción interatómica está dado por las superficies de energía potencial . En general, las superficies de energía potencial están acopladas a través de los términos de acoplamiento vibrónico . [59]

Los métodos más populares para propagar el paquete de ondas asociado a la geometría molecular son:

Técnica del operador dividido

La forma en que un método computacional resuelve ecuaciones cuánticas afecta la precisión y la eficiencia del método. La técnica del operador dividido es uno de estos métodos para resolver ecuaciones diferenciales. En química computacional, la técnica del operador dividido reduce los costos computacionales de la simulación de sistemas químicos. Los costos computacionales son aproximadamente el tiempo que les toma a las computadoras calcular estos sistemas químicos, ya que puede llevar días para sistemas más complejos. Los sistemas cuánticos son difíciles y requieren mucho tiempo para ser resueltos por humanos. Los métodos del operador dividido ayudan a las computadoras a calcular estos sistemas rápidamente al resolver los subproblemas en una ecuación diferencial cuántica . El método hace esto al separar la ecuación diferencial en dos ecuaciones diferentes, como cuando hay más de dos operadores. Una vez resueltas, las ecuaciones divididas se combinan nuevamente en una ecuación para dar una solución fácilmente calculable. [62]

Este método se utiliza en muchos campos que requieren la resolución de ecuaciones diferenciales, como la biología . Sin embargo, la técnica conlleva un error de división. Por ejemplo, con la siguiente solución para una ecuación diferencial. [62]

La ecuación se puede descomponer, pero las soluciones no serán exactas, solo similares. Este es un ejemplo de descomposición de primer orden. [62]

Hay formas de reducir este error, que incluyen tomar un promedio de dos ecuaciones divididas. [62]

Otra forma de aumentar la precisión es utilizar la división de orden superior. Por lo general, la división de segundo orden es la más utilizada porque la división de orden superior requiere mucho más tiempo para calcularse y no vale la pena el costo. Los métodos de orden superior se vuelven demasiado difíciles de implementar y no son útiles para resolver ecuaciones diferenciales a pesar de la mayor precisión. [62]

Los químicos computacionales dedican mucho tiempo a hacer que los sistemas calculados con la técnica del operador dividido sean más precisos y, al mismo tiempo, minimicen el costo computacional. Calcular métodos es un desafío enorme para muchos químicos que intentan simular moléculas o entornos químicos. [62]

C 60 con isosuperficie de densidad electrónica del estado fundamental calculada con DFT

Métodos funcionales de densidad

Los métodos de la teoría funcional de la densidad (DFT) suelen considerarse métodos ab initio para determinar la estructura electrónica molecular, aunque muchos de los funcionales más comunes utilizan parámetros derivados de datos empíricos o de cálculos más complejos. En la DFT, la energía total se expresa en términos de la densidad total de un electrón en lugar de la función de onda. En este tipo de cálculo, existe un hamiltoniano aproximado y una expresión aproximada para la densidad total de electrones. Los métodos DFT pueden ser muy precisos con un bajo costo computacional. Algunos métodos combinan el funcional de intercambio de la densidad con el término de intercambio de Hartree-Fock y se denominan métodos funcionales híbridos . [63]

Métodos semiempíricos

Los métodos semiempíricos de química cuántica se basan en el formalismo del método Hartree-Fock , pero realizan muchas aproximaciones y obtienen algunos parámetros a partir de datos empíricos. Fueron muy importantes en la química computacional desde los años 60 hasta los 90, especialmente para tratar moléculas grandes, donde el método Hartree-Fock completo sin las aproximaciones era demasiado costoso. El uso de parámetros empíricos parece permitir cierta inclusión de efectos de correlación en los métodos. [64]

Los métodos semiempíricos primitivos fueron diseñados incluso antes, donde la parte de dos electrones del hamiltoniano no está incluida explícitamente. Para los sistemas de electrones π, este fue el método de Hückel propuesto por Erich Hückel , y para todos los sistemas de electrones de valencia, el método de Hückel extendido propuesto por Roald Hoffmann . A veces, los métodos de Hückel se denominan "completamente empíricos" porque no derivan de un hamiltoniano. [65] Sin embargo, el término "métodos empíricos" o "campos de fuerza empíricos" se usa generalmente para describir la mecánica molecular. [66]

Función de energía potencial de mecánica molecular con disolvente continuo

Mecánica molecular

En muchos casos, se pueden modelar con éxito sistemas moleculares grandes evitando por completo los cálculos mecánicos cuánticos. Las simulaciones de mecánica molecular , por ejemplo, utilizan una expresión clásica para la energía de un compuesto, por ejemplo, el oscilador armónico . Todas las constantes que aparecen en las ecuaciones deben obtenerse de antemano a partir de datos experimentales o cálculos ab initio . [64]

La base de datos de compuestos utilizados para la parametrización, es decir, el conjunto resultante de parámetros y funciones se denomina campo de fuerza , y es crucial para el éxito de los cálculos de mecánica molecular. Se esperaría que un campo de fuerza parametrizado contra una clase específica de moléculas, por ejemplo, proteínas, solo tuviera relevancia al describir otras moléculas de la misma clase. [64] Estos métodos se pueden aplicar a proteínas y otras moléculas biológicas grandes, y permiten estudios del enfoque e interacción (acoplamiento) de posibles moléculas de fármacos. [67] [68]

Dinámica molecular del gas argón

Dinámica molecular

La dinámica molecular (MD) utiliza la mecánica cuántica , la mecánica molecular o una mezcla de ambas para calcular fuerzas que luego se utilizan para resolver las leyes de movimiento de Newton y examinar el comportamiento dependiente del tiempo de los sistemas. El resultado de una simulación de dinámica molecular es una trayectoria que describe cómo la posición y la velocidad de las partículas varían con el tiempo. El punto de fase de un sistema descrito por las posiciones y los momentos de todas sus partículas en un punto de tiempo anterior determinará el siguiente punto de fase en el tiempo mediante la integración sobre las leyes de movimiento de Newton. [69]

Montecarlo

Monte Carlo (MC) genera configuraciones de un sistema haciendo cambios aleatorios en las posiciones de sus partículas, junto con sus orientaciones y conformaciones cuando sea apropiado. [70] Es un método de muestreo aleatorio, que hace uso del llamado muestreo de importancia . Los métodos de muestreo de importancia son capaces de generar estados de baja energía, ya que esto permite calcular las propiedades con precisión. La energía potencial de cada configuración del sistema se puede calcular, junto con los valores de otras propiedades, a partir de las posiciones de los átomos. [71] [72]

Mecánica cuántica/mecánica molecular (QM/MM)

QM/MM es un método híbrido que intenta combinar la precisión de la mecánica cuántica con la velocidad de la mecánica molecular. Es útil para simular moléculas muy grandes como las enzimas . [73]

Química computacional cuántica

La química computacional cuántica tiene como objetivo explotar la computación cuántica para simular sistemas químicos, lo que la distingue del enfoque QM/MM (mecánica cuántica/mecánica molecular). [74] Mientras que QM/MM utiliza un enfoque híbrido, combinando la mecánica cuántica para una parte del sistema con la mecánica clásica para el resto, la química computacional cuántica utiliza exclusivamente métodos de computación cuántica para representar y procesar información, como los operadores hamiltonianos. [75]

Los métodos convencionales de química computacional suelen tener dificultades para resolver las complejas ecuaciones de la mecánica cuántica, en particular debido al crecimiento exponencial de la función de onda de un sistema cuántico. La química computacional cuántica aborda estos desafíos utilizando métodos de computación cuántica , como la qubitización y la estimación de fase cuántica , que se cree que ofrecen soluciones escalables. [76]

La qubitización implica adaptar el operador hamiltoniano para un procesamiento más eficiente en computadoras cuánticas, mejorando la eficiencia de la simulación. La estimación de fase cuántica, por otro lado, ayuda a determinar con precisión los estados propios de energía, que son fundamentales para comprender el comportamiento del sistema cuántico. [77]

Si bien estas técnicas han hecho avanzar el campo de la química computacional, especialmente en la simulación de sistemas químicos, su aplicación práctica actualmente se limita principalmente a sistemas más pequeños debido a limitaciones tecnológicas. No obstante, estos avances pueden conducir a un progreso significativo hacia la consecución de simulaciones de química cuántica más precisas y eficientes en el uso de recursos. [76]

Costos computacionales en algoritmos de química

El costo computacional y la complejidad algorítmica en química se utilizan para ayudar a comprender y predecir fenómenos químicos. Ayudan a determinar qué algoritmos o métodos computacionales utilizar al resolver problemas químicos. Esta sección se centra en la escala de la complejidad computacional con el tamaño de la molécula y detalla los algoritmos que se utilizan comúnmente en ambos dominios. [78]

En química cuántica, en particular, la complejidad puede crecer exponencialmente con el número de electrones involucrados en el sistema. Este crecimiento exponencial es una barrera importante para simular sistemas grandes o complejos con precisión. [79]

Los algoritmos avanzados en ambos campos buscan equilibrar la precisión con la eficiencia computacional. Por ejemplo, en la química cuántica, se emplean métodos como la integración de Verlet o el algoritmo de Beeman por su eficiencia computacional. En la química cuántica, se utilizan cada vez más métodos híbridos que combinan diferentes enfoques computacionales (como QM/MM) para abordar grandes sistemas biomoleculares. [80]

Ejemplos de complejidad algorítmica

La siguiente lista ilustra el impacto de la complejidad computacional en los algoritmos utilizados en los cálculos químicos. Es importante señalar que, si bien esta lista proporciona ejemplos clave, no es exhaustiva y sirve como guía para comprender cómo las demandas computacionales influyen en la selección de métodos computacionales específicos en química.

Dinámica molecular

Algoritmo

Resuelve las ecuaciones de movimiento de Newton para átomos y moléculas. [81]

Simulación de dinámica molecular de agua líquida a 298 K

Complejidad

El cálculo estándar de interacción por pares en MD genera complejidad para las partículas. Esto se debe a que cada partícula interactúa con todas las demás partículas, lo que da como resultado interacciones. [82] Los algoritmos avanzados, como la suma de Ewald o el método multipolar rápido, reducen esto a o incluso agrupando partículas distantes y tratándolas como una sola entidad o utilizando aproximaciones matemáticas inteligentes. [83] [84]

Mecánica cuántica/mecánica molecular (QM/MM)

Algoritmo

Combina cálculos mecánicos cuánticos para una región pequeña con mecánica molecular para un entorno más amplio. [85]

Complejidad

La complejidad de los métodos QM/MM depende tanto del tamaño de la región cuántica como del método utilizado para los cálculos cuánticos. Por ejemplo, si se utiliza un método Hartree-Fock para la parte cuántica, la complejidad se puede aproximar como , donde es el número de funciones base en la región cuántica. Esta complejidad surge de la necesidad de resolver un conjunto de ecuaciones acopladas de forma iterativa hasta que se logre la autoconsistencia. [86]

Diagrama de flujo algorítmico que ilustra el método Hartree-Fock

Método Hartree-Fock

Algoritmo

Encuentra un único estado de Fock que minimiza la energía. [87]

Complejidad

NP-hard o NP-complete como se demuestra al incorporar instancias del modelo de Ising en los cálculos de Hartree-Fock. El método de Hartree-Fock implica la resolución de las ecuaciones de Roothaan-Hall, que escalan en función de la implementación, siendo el número de funciones base. El costo computacional proviene principalmente de la evaluación y transformación de las integrales de dos electrones. Esta prueba de NP-hardness o NP-completeness proviene de la incorporación de problemas como el modelo de Ising en el formalismo de Hartree-Fock. [87]

Molécula de acroleína . La DFT proporciona buenos resultados en la predicción de la sensibilidad de algunas nanoestructuras a contaminantes ambientales como la acroleína. [88]

Teoría del funcional de la densidad

Algoritmo

Investiga la estructura electrónica o estructura nuclear de sistemas de muchos cuerpos como átomos, moléculas y fases condensadas . [89]

Complejidad

Las implementaciones tradicionales de DFT suelen escalar como , principalmente debido a la necesidad de diagonalizar la matriz de Kohn-Sham . [90] El paso de diagonalización, que encuentra los valores propios y los vectores propios de la matriz, contribuye más a este escalamiento. Los avances recientes en DFT apuntan a reducir esta complejidad a través de varias aproximaciones y mejoras algorítmicas. [91]

Método estándar CCSD y CCSD(T)

Algoritmo

Los métodos CCSD y CCSD(T) son técnicas avanzadas de estructura electrónica que implican excitaciones simples, dobles y, en el caso de CCSD(T), triples perturbativas para calcular los efectos de correlación electrónica. [92]

Complejidad

CCSD

Escalas como donde es el número de funciones base. Esta intensa demanda computacional surge de la inclusión de excitaciones simples y dobles en el cálculo de correlación electrónica. [92]

CCSD(T)

Con la adición de triples perturbativos, la complejidad aumenta a . Esta complejidad elevada restringe el uso práctico a sistemas más pequeños, típicamente hasta 20-25 átomos en implementaciones convencionales. [92]

Diagrama de densidad electrónica del orbital molecular 2a1 del metano en el nivel CCSD(T)/cc-pVQZ. Gráfico creado con Molden basado en la optimización de geometría correlacionada con CFOUR en el nivel CCSD(T) en base cc-pVQZ.

Método CCSD(T) de escala lineal

Algoritmo

Una adaptación del método estándar CCSD(T) que utiliza orbitales naturales locales (NO) para reducir significativamente la carga computacional y permitir la aplicación a sistemas más grandes. [92]

Complejidad

Se logra una escala lineal con el tamaño del sistema, una mejora importante con respecto a la escala tradicional de quinta potencia del CCSD. Este avance permite aplicaciones prácticas para moléculas de hasta 100 átomos con conjuntos de bases razonables, lo que marca un avance significativo en la capacidad de la química computacional para manejar sistemas más grandes con alta precisión. [92]

La demostración de las clases de complejidad de los algoritmos implica una combinación de pruebas matemáticas y experimentos computacionales. Por ejemplo, en el caso del método Hartree-Fock, la demostración de la NP-dureza es un resultado teórico derivado de la teoría de la complejidad, específicamente a través de reducciones de problemas NP-duros conocidos. [93]

En el caso de otros métodos, como MD o DFT, la complejidad computacional suele observarse empíricamente y respaldarse mediante análisis de algoritmos. En estos casos, la prueba de corrección tiene menos que ver con pruebas matemáticas formales y más con la observación consistente del comportamiento computacional en varios sistemas e implementaciones. [93]

Exactitud

La química computacional no es una descripción exacta de la química de la vida real, ya que los modelos matemáticos y físicos de la naturaleza sólo pueden proporcionar una aproximación. Sin embargo, la mayoría de los fenómenos químicos pueden describirse hasta cierto punto en un esquema computacional cualitativo o cuantitativo aproximado. [94]

Las moléculas están formadas por núcleos y electrones, por lo que se aplican los métodos de la mecánica cuántica . Los químicos computacionales a menudo intentan resolver la ecuación de Schrödinger no relativista , con correcciones relativistas añadidas, aunque se han logrado algunos avances en la resolución de la ecuación de Dirac totalmente relativista . En principio, es posible resolver la ecuación de Schrödinger en su forma dependiente o independiente del tiempo, según sea apropiado para el problema en cuestión; en la práctica, esto no es posible excepto para sistemas muy pequeños. Por lo tanto, una gran cantidad de métodos aproximados intentan lograr el mejor equilibrio entre precisión y costo computacional. [95]

La precisión siempre se puede mejorar con un mayor costo computacional. Pueden presentarse errores significativos en modelos ab initio que comprenden muchos electrones, debido al costo computacional de los métodos que incluyen la relatividad total. [92] Esto complica el estudio de moléculas que interactúan con átomos de unidades de masa atómica alta, como los metales de transición y sus propiedades catalíticas. Los algoritmos actuales en química computacional pueden calcular rutinariamente las propiedades de moléculas pequeñas que contienen hasta aproximadamente 40 electrones con errores para energías menores a unos pocos kJ/mol. Para las geometrías, las longitudes de enlace se pueden predecir con una precisión de unos pocos picómetros y los ángulos de enlace con una precisión de 0,5 grados. El tratamiento de moléculas más grandes que contienen unas pocas docenas de átomos es computacionalmente manejable con métodos más aproximados como la teoría funcional de la densidad (DFT). [96]

Existe cierta controversia en el campo sobre si estos últimos métodos son suficientes o no para describir reacciones químicas complejas, como las de la bioquímica. Las moléculas grandes se pueden estudiar mediante métodos aproximados semiempíricos. Incluso las moléculas más grandes se tratan mediante métodos de mecánica clásica que utilizan lo que se denomina mecánica molecular (MM). En los métodos QM-MM, pequeñas partes de grandes complejos se tratan de forma mecánica cuántica (QM) y el resto se trata de forma aproximada (MM). [97]

Paquetes de software

Existen muchos paquetes de software de química computacional autosuficientes . Algunos incluyen muchos métodos que cubren un amplio espectro, mientras que otros se concentran en un rango muy específico o incluso en un solo método. Los detalles de la mayoría de ellos se pueden encontrar en:

Revistas especializadas en química computacional

Enlaces externos

Wikimedia Commons tiene medios relacionados con Química computacional .

Véase también

Referencias

  1. ^ "WebMO". www.webmo.net . Consultado el 5 de diciembre de 2023 .
  2. ^ Parrill, Abby L.; Lipkowitz, Kenny B., eds. (19 de octubre de 2018). Reseñas en química computacional, volumen 31. Vol. 4 (1.ª ed.). Wiley. doi :10.1002/series6143. ISBN 978-1-119-51802-0.
  3. ^ Comité sobre Desafíos para las Ciencias Químicas en el Siglo XXI del Consejo Nacional de Investigación (EE. UU.) (2003), "Teoría química y modelado computacional: de la química computacional a la ingeniería de sistemas de procesos", Más allá de la frontera molecular: desafíos para la química y la ingeniería química , National Academies Press (EE. UU.) , consultado el 5 de diciembre de 2023
  4. ^ Korobov, Vladimir I.; Karr, J.-Ph. (7 de septiembre de 2021). "Transiciones rovibratorias promediadas por espín en los iones moleculares de hidrógeno". Physical Review A . 104 (3): 032806. arXiv : 2107.14497 . Código Bibliográfico :2021PhRvA.104c2806K. doi :10.1103/PhysRevA.104.032806. S2CID  236635049.
  5. ^ Nozières, Philippe (1997). Teoría de los sistemas de Fermi en interacción . Libros clásicos avanzados. Cambridge, Mass.: Perseus Publishing. ISBN 978-0-201-32824-0.
  6. ^ Willems, Henriëtte; De Cesco, Stephane; Svensson, Fredrik (24 de septiembre de 2020). "Química computacional con un presupuesto limitado: apoyo al descubrimiento de fármacos con recursos limitados: miniperspectiva". Revista de química medicinal . 63 (18): 10158–10169. doi :10.1021/acs.jmedchem.9b02126. ISSN  0022-2623. PMID  32298123. S2CID  215802432.
  7. ^ Cramer, Christopher J. (2014). Fundamentos de química computacional: teorías y modelos . Chichester: Wiley. ISBN 978-0-470-09182-1.
  8. ^ ab Patel, Prajay; Melin, Timothé RL; North, Sasha C.; Wilson, Angela K. (1 de enero de 2021), Dixon, David A. (ed.), "Capítulo cuatro: metodologías compuestas ab initio: su importancia para la comunidad química", Annual Reports in Computational Chemistry , vol. 17, Elsevier, págs. 113–161, doi :10.1016/bs.arcc.2021.09.002, S2CID  244017999 , consultado el 3 de diciembre de 2023
  9. ^ Heitler, W.; Londres, F. (1 de junio de 1927). "Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik". Zeitschrift für Physik (en alemán). 44 (6): 455–472. Código Bib : 1927ZPhy...44..455H. doi :10.1007/BF01397394. ISSN  0044-3328. S2CID  119739102.
  10. ^ Pauling, Linus ; Wilson, Edgar Bright (1985). Introducción a la mecánica cuántica: con aplicaciones a la química . Nueva York: Dover publications. ISBN 978-0-486-64871-2.
  11. ^ Eyring, Henry ; Walter, John; Kimball, George E. (1967). Química cuántica (14.ª edición). Nueva York: Wiley. ISBN 978-0-471-24981-8.
  12. ^ Heitler, W. (1 de enero de 1956). Mecánica ondulatoria elemental con aplicaciones a la química cuántica (2.ª edición). Oxford University Press. ISBN 978-0-19-851103-8.
  13. ^ Coulson, Charles Alfred ; McWeeny, Roy (1991). Valencia de Coulson . Oxford science publications (3.ª ed.). Oxford Nueva York Toronto [etc.]: Oxford university press. ISBN 978-0-19-855145-4.
  14. ^ ab Roothaan, CCJ (1 de abril de 1951). "Nuevos desarrollos en la teoría de orbitales moleculares". Reseñas de física moderna . 23 (2): 69–89. Bibcode :1951RvMP...23...69R. doi :10.1103/RevModPhys.23.69.
  15. ^ ab Ruedenberg, Klaus (1954-11-01). "Modelo de red de electrones libres para sistemas conjugados. V. Energías y distribuciones de electrones en el modelo de OM de electrones libres y en el modelo de OM de electrones libres conjugados". Revista de Física Química . 22 (11): 1878–1894. Bibcode :1954JChPh..22.1878R. doi :10.1063/1.1739935. ISSN  0021-9606.
  16. ^ Smith, SJ; Sutcliffe, BT (1997). "El desarrollo de la química computacional en el Reino Unido". Reseñas en química computacional . 10 : 271–316.
  17. ^ Boys, SF; Cook, GB; Reeves, CM; Shavitt, I. (1956-12-01) [1 de diciembre de 1956]. "Cálculos fundamentales automáticos de la estructura molecular". Nature . 178 (4544): 1207–1209. Bibcode :1956Natur.178.1207B. doi :10.1038/1781207a0. ISSN  1476-4687. S2CID  4218995.
  18. ^ Schaefer, Henry F. III (1972). La estructura electrónica de átomos y moléculas . Reading, Massachusetts: Addison-Wesley Publishing Co. pág. 146.
  19. ^ Boys, SF ; Cook, GB; Reeves, CM; Shavitt, I. (1956). "Cálculos fundamentales automáticos de la estructura molecular". Nature . 178 (2): 1207. Bibcode :1956Natur.178.1207B. doi :10.1038/1781207a0. S2CID  4218995.
  20. ^ Richards, WG; Walker, TEH; Hinkley RK (1971). Una bibliografía de funciones de onda moleculares ab initio . Oxford: Clarendon Press.
  21. ^ Preuss, H. (1968). "DasSCF-MO-P (LCGO) -Verfahren und seine Varianten". Revista Internacional de Química Cuántica . 2 (5): 651. Código bibliográfico : 1968IJQC....2..651P. doi :10.1002/qua.560020506.
  22. ^ Buenker, RJ; Peyerimhoff, SD (1969). "Cálculos de SCF ab initio para azuleno y naftaleno". Chemical Physics Letters . 3 (1): 37. Bibcode :1969CPL.....3...37B. doi :10.1016/0009-2614(69)80014-X.
  23. ^ Schaefer, Henry F. III (1984). Química cuántica . Oxford: Clarendon Press.
  24. ^ Streitwieser, A.; Brauman, JI; Coulson, CA (1965). Tablas suplementarias de cálculos de orbitales moleculares . Oxford: Pergamon Press.
  25. ^ Pople, John A .; Beveridge, David L. (1970). Teoría aproximada de orbitales moleculares . Nueva York: McGraw Hill.
  26. ^ ab Ma, Xiaoyue (1 de diciembre de 2022). "Desarrollo de la química computacional y aplicación de métodos computacionales". Journal of Physics: Conference Series . 2386 (1): 012005. Bibcode :2022JPhCS2386a2005M. doi : 10.1088/1742-6596/2386/1/012005 . ISSN  1742-6588.
  27. ^ Allinger, Norman (1977). "Análisis conformacional. 130. MM2. Un campo de fuerza de hidrocarburos que utiliza términos torsionales V1 y V2". Revista de la Sociedad Química Americana . 99 (25): 8127–8134. doi :10.1021/ja00467a001.
  28. ^ Fernbach, Sidney; Taub, Abraham Haskell (1970). Las computadoras y su papel en las ciencias físicas . Routledge. ISBN 978-0-677-14030-8.
  29. ^ Kenny B. Lipkowitz; Donald B. Boyd, eds. (1990). "vol 1, prefacio". Reseñas en Química Computacional . Vol. 1. Wiley. doi :10.1002/9780470125786. ISBN 978-0-470-12578-6.
  30. ^ "El Premio Nobel de Química 1998".
  31. ^ "El Premio Nobel de Química 2013" (Nota de prensa). Real Academia Sueca de Ciencias. 9 de octubre de 2013. Consultado el 9 de octubre de 2013 .
  32. ^ Musil, Felix; Grisafi, Andrea; Bartók, Albert P.; Ortner, Christoph; Csányi, Gábor; Ceriotti, Michele (25 de agosto de 2021). "Representaciones estructurales inspiradas en la física para moléculas y materiales". Chemical Reviews . 121 (16): 9759–9815. arXiv : 2101.04673 . doi : 10.1021/acs.chemrev.1c00021 . ISSN  0009-2665. PMID  34310133.
  33. ^ Muresan, Sorel; Sitzmann, Markus; Southan, Christopher (2012), Larson, Richard S. (ed.), "Mapeo entre bases de datos de compuestos y objetivos proteicos", Bioinformática y descubrimiento de fármacos , Métodos en biología molecular, vol. 910, Totowa, NJ: Humana Press, págs. 145-164, doi :10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-965-5, PMC  7449375 , PMID  22821596 , consultado el 3 de diciembre de 2023
  34. ^ Roy, Kunal; Kar, Supratik; Das, Rudra Narayan (2015). Comprensión de los conceptos básicos de QSAR para aplicaciones en ciencias farmacéuticas y evaluación de riesgos . Ámsterdam, Boston: Elsevier/Academic Press. ISBN 978-0-12-801505-6.
  35. ^ Feng, Fan; Lai, Luhua; Pei, Jianfeng (2018). "Análisis de síntesis química computacional y diseño de vías". Frontiers in Chemistry . 6 : 199. doi : 10.3389/fchem.2018.00199 . ISSN  2296-2646. PMC 5994992 . PMID  29915783. 
  36. ^ ab Tsui, Vickie; Ortwine, Daniel F.; Blaney, Jeffrey M. (1 de marzo de 2017). "Habilitación de decisiones en proyectos de descubrimiento de fármacos con química computacional integrada e informática". Revista de diseño molecular asistido por computadora . 31 (3): 287–291. Bibcode :2017JCAMD..31..287T. doi :10.1007/s10822-016-9988-y. ISSN  1573-4951. PMID  27796615. S2CID  23373414.
  37. ^ Elnabawy, Ahmed O.; Rangarajan, Srinivas; Mavrikakis, Manos (1 de agosto de 2015). "Química computacional para la síntesis de NH3, hidrotratamiento y reducción de NOx: tres temas de especial interés para Haldor Topsøe". Journal of Catalysis . Número especial: El impacto de Haldor Topsøe en la catálisis. 328 : 26–35. doi :10.1016/j.jcat.2014.12.018. ISSN  0021-9517.
  38. ^ abc Patel, Prajay; Wilson, Angela K. (1 de diciembre de 2020). "Consideraciones de química computacional en catálisis: regioselectividad y disociación metal-ligando". Catálisis hoy . Actas de la 3.ª Conferencia internacional sobre catálisis e ingeniería química. 358 : 422–429. doi : 10.1016/j.cattod.2020.07.057 . ISSN  0920-5861. S2CID  225472601.
  39. ^ ab van Santen, RA (6 de mayo de 1996). "Avances químicos computacionales en catálisis heterogénea". Journal of Molecular Catalysis A: Chemical . Actas del 8º Simposio Internacional sobre las Relaciones entre Catálisis Homogénea y Heterogénea. 107 (1): 5–12. doi :10.1016/1381-1169(95)00161-1. ISSN  1381-1169. S2CID  59580128.
  40. ^ van Vlijmen, Herman; Desjarlais, Renee L.; Mirzadegan, Tara (marzo de 2017). "Química computacional en Janssen". Revista de diseño molecular asistido por ordenador . 31 (3): 267–273. Bibcode :2017JCAMD..31..267V. doi :10.1007/s10822-016-9998-9. ISSN  1573-4951. PMID  27995515. S2CID  207166545.
  41. ^ Ahmad, Imad; Kuznetsov, Aleksey E.; Pirzada, Abdul Saboor; Alsharif, Khalaf F.; Daglia, Maria; Khan, Haroon (2023). "Farmacología computacional y química computacional de la 4-hidroxiisoleucina: enfoques fisicoquímicos, farmacocinéticos y basados ​​en DFT". Frontiers in Chemistry . 11 . Bibcode :2023FrCh...1145974A. doi : 10.3389/fchem.2023.1145974 . ISSN  2296-2646. PMC 10133580 . PMID  37123881. 
  42. ^ El-Mageed, HR Abd; Mustafa, FM; Abdel-Latif, Mahmoud K. (2 de enero de 2022). "Nanoclusters, nanopartículas y nanotubos de nitruro de boro como portador de fármacos para el fármaco antituberculoso isoniazida, enfoques de química computacional". Revista de estructura y dinámica biomolecular . 40 (1): 226–235. doi :10.1080/07391102.2020.1814871. ISSN  0739-1102. PMID  32870128. S2CID  221403943.
  43. ^ abcde Muresan, Sorel; Sitzmann, Markus; Southan, Christopher (2012), Larson, Richard S. (ed.), "Mapeo entre bases de datos de compuestos y objetivos proteicos", Bioinformática y descubrimiento de fármacos , Métodos en biología molecular, vol. 910, Totowa, NJ: Humana Press, págs. 145-164, doi :10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-964-8, PMC  7449375 , PMID  22821596
  44. ^ Gilson, Michael K.; Liu, Tiqing; Baitaluk, Michael; Nicola, George; Hwang, Linda; Chong, Jenny (4 de enero de 2016). "BindingDB en 2015: una base de datos pública para química medicinal, química computacional y farmacología de sistemas". Investigación de ácidos nucleicos . 44 (D1): D1045–1053. doi :10.1093/nar/gkv1072. ISSN  1362-4962. PMC 4702793 . PMID  26481362. 
  45. ^ Zardecki, Christine; Dutta, Shuchismita; Goodsell, David S.; Voigt, Maria; Burley, Stephen K. (8 de marzo de 2016). "Banco de datos de proteínas RCSB: un recurso para exploraciones químicas, bioquímicas y estructurales de biomoléculas grandes y pequeñas". Revista de educación química . 93 (3): 569–575. Código Bibliográfico :2016JChEd..93..569Z. doi : 10.1021/acs.jchemed.5b00404 . ISSN  0021-9584.
  46. ^ "Química computacional y modelado molecular". SpringerLink . 2008. doi :10.1007/978-3-540-77304-7. ISBN 978-3-540-77302-3.S2CID102140015  .​
  47. ^ Leach, Andrew R. (2009). Modelado molecular: principios y aplicaciones (2.ª ed., 12.ª ed. [Dr.]). Harlow: Pearson/Prentice Hall. ISBN 978-0-582-38210-7.
  48. ^ Xu, Peng; Westheimer, Bryce M.; Schlinsog, Megan; Sattasathuchana, Tosaporn; Elliott, George; Gordon, Mark S.; Guidez, Emilie (1 de enero de 2024). "El potencial de fragmento efectivo: un campo de fuerza ab initio". Química computacional integral : 153–161. doi :10.1016/B978-0-12-821978-2.00141-0. ISBN 978-0-12-823256-9.
  49. ^ Friesner, Richard A. (10 de mayo de 2005). "Química cuántica ab initio: metodología y aplicaciones". Actas de la Academia Nacional de Ciencias . 102 (19): 6648–6653. doi : 10.1073/pnas.0408036102 . ISSN  0027-8424. PMC 1100737 . PMID  15870212. 
  50. ^ ab Hinchliffe, Alan (2001). Modelado de estructuras moleculares . Serie de Wiley en química teórica (2.ª edición, reimpresión). Chichester: Wiley. ISBN 978-0-471-48993-1.
  51. ^ S, DR Hartree FR (1 de enero de 1947). "El cálculo de estructuras atómicas". Informes sobre el progreso en física . 11 (1): 113–143. Bibcode :1947RPPh...11..113S. doi :10.1088/0034-4885/11/1/305. S2CID  250826906.
  52. ^ Møller, Chr.; Plesset, MS (1934-10-01). "Nota sobre un tratamiento de aproximación para sistemas de muchos electrones". Physical Review . 46 (7): 618–622. Bibcode :1934PhRv...46..618M. doi :10.1103/PhysRev.46.618. ISSN  0031-899X.
  53. ^ ab Matveeva, Regina; Folkestad, Sarai Dery; Høyvik, Ida-Marie (9 de febrero de 2023). "Teoría de Hartree-Fock de ruptura de partículas para sistemas moleculares abiertos". The Journal of Physical Chemistry A . 127 (5). Sociedad Química Estadounidense: 1329–1341. Código Bibliográfico :2023JPCA..127.1329M. doi :10.1021/acs.jpca.2c07686. ISSN  1089-5639. PMC 9923758 . PMID  36720055. 
  54. ^ McLACHLAN, AD; BALL, MA (1964-07-01). "Teoría de Hartree-Fock dependiente del tiempo para moléculas". Reseñas de Física Moderna . 36 (3): 844–855. Bibcode :1964RvMP...36..844M. doi :10.1103/RevModPhys.36.844.
  55. ^ Cohen, Maurice; Kelly, Paul S. (1967-05-01). "FUNCIONES DE ONDA DE HARTREE-FOCK PARA ESTADOS EXCITADOS: III. TRANSICIONES DIPOLARES EN SISTEMAS DE TRES ELECTRONES". Revista Canadiense de Física . 45 (5): 1661–1673. Bibcode :1967CaJPh..45.1661C. doi :10.1139/p67-129. ISSN  0008-4204.
  56. ^ Ballard, Andrew J.; Das, Ritankar; Martiniani, Stefano; Mehta, Dhagash; Sagun, Levent; Stevenson, Jacob D.; Wales, David J. (24 de mayo de 2017). "Paisajes energéticos para el aprendizaje automático". Química física Física química . 19 (20): 12585–12603. arXiv : 1703.07915 . Código Bibliográfico :2017PCCP...1912585B. doi :10.1039/C7CP01108C. ISSN  1463-9084. PMID  28367548.
  57. ^ Ohlinger, WS; Klunzinger, PE; Deppmeier, BJ; Hehre, WJ (12 de marzo de 2009). "Cálculo eficiente de calores de formación". The Journal of Physical Chemistry A . 113 (10): 2165–2175. doi :10.1021/jp810144q. ISSN  1089-5639. PMID  19222177.
  58. ^ Butler, Laurie J. (octubre de 1998). "Dinámica de la reacción química más allá de la aproximación de Born-Oppenheimer". Revista anual de química física . 49 (1): 125–171. Bibcode :1998ARPC...49..125B. doi :10.1146/annurev.physchem.49.1.125. ISSN  0066-426X. PMID  15012427.
  59. ^ Ito, Kenichi; Nakamura, Shu (junio de 2010). "Teoría de dispersión dependiente del tiempo para operadores de Schrödinger en variedades de dispersión". Journal of the London Mathematical Society . 81 (3): 774–792. arXiv : 0810.1575 . doi :10.1112/jlms/jdq018. S2CID  8115409.
  60. ^ Ambrose, D; Counsell, J. F; Davenport, A. J (1970-03-01). "El uso de polinomios de Chebyshev para la representación de presiones de vapor entre el punto triple y el punto crítico". The Journal of Chemical Thermodynamics . 2 (2): 283–294. Bibcode :1970JChTh...2..283A. doi :10.1016/0021-9614(70)90093-5. ISSN  0021-9614.
  61. ^ Manthe, U.; Meyer, H.-D.; Cederbaum, LS (1992-09-01). "Dinámica de paquetes de ondas dentro del marco multiconfiguracional de Hartree: aspectos generales y aplicación a NOCl". The Journal of Chemical Physics . 97 (5): 3199–3213. Bibcode :1992JChPh..97.3199M. doi :10.1063/1.463007. ISSN  0021-9606.
  62. ^ abcdefg Lukassen, Axel Ariaan; Kiehl, Martin (15 de diciembre de 2018). "División de operadores para sistemas de reacción química con química rápida". Revista de Matemática Computacional y Aplicada . 344 : 495–511. doi : 10.1016/j.cam.2018.06.001 . ISSN  0377-0427. S2CID  49612142.
  63. ^ De Proft, Frank; Geerlings, Paul; Heidar-Zadeh, Farnaz; Ayers, Paul W. (1 de enero de 2024). "Teoría conceptual del funcional de la densidad". Química computacional integral : 306–321. doi :10.1016/B978-0-12-821978-2.00025-8. ISBN 978-0-12-823256-9.
  64. ^ abc Ramachandran, KI; Deepa, G.; Namboori, K. (2008). Química computacional y modelado molecular: principios y aplicaciones . Berlín: Springer. ISBN 978-3-540-77304-7.
  65. ^ Counts, Richard W. (1 de julio de 1987). "Estrategias I". Revista de diseño molecular asistido por ordenador . 1 (2): 177–178. Código Bibliográfico :1987JCAMD...1..177C. doi :10.1007/bf01676961. ISSN  0920-654X. PMID  3504968. S2CID  40429116.
  66. ^ Dinur, Uri; Hagler, Arnold T. (1991). Lipkowitz, Kenny B.; Boyd, Donald B. (eds.). Reseñas en Química Computacional . John Wiley & Sons, Inc. págs. 99–164. doi :10.1002/9780470125793.ch4. ISBN 978-0-470-12579-3.
  67. ^ Rubenstein, Lester A.; Zauhar, Randy J.; Lanzara, Richard G. (2006). "Molecular dynamics of a biophysical model for β2-adrenergic and G protein-coupled receptor activation" (PDF) . Revista de gráficos moleculares y modelado . 25 (4): 396–409. doi :10.1016/j.jmgm.2006.02.008. PMID  16574446. Archivado (PDF) desde el original el 27 de febrero de 2008.
  68. ^ Rubenstein, Lester A.; Lanzara, Richard G. (1998). "La activación de los receptores acoplados a la proteína G implica la modulación de la unión del agonista por cisteína" (PDF) . Journal of Molecular Structure: THEOCHEM . 430 : 57–71. doi :10.1016/S0166-1280(98)90217-2. Archivado (PDF) desde el original el 30 de mayo de 2004.
  69. ^ Hutter, Jürg; Iannuzzi, Marcella; Kühne, Thomas D. (1 de enero de 2024). "Ab Initio Molecular Dynamics: A Guide to Applications". Química computacional integral : 493–517. doi :10.1016/B978-0-12-821978-2.00096-9. ISBN 978-0-12-823256-9.
  70. ^ Satoh, A. (1 de enero de 2003), Satoh, A. (ed.), "Capítulo 3 - Métodos de Monte Carlo", Estudios en ciencia de la interfaz , Introducción a la microsimulación molecular de dispersiones coloidales, vol. 17, Elsevier, págs. 19-63, doi :10.1016/S1383-7303(03)80031-5, ISBN 978-0-444-51424-0, consultado el 3 de diciembre de 2023
  71. ^ Allen, MP (1987). Simulación por ordenador de líquidos . DJ Tildesley. Oxford [Inglaterra]: Clarendon Press. ISBN 0-19-855375-7.OCLC 15132676  .
  72. ^ McArdle, Sam; Endo, Suguru; Aspuru-Guzik, Alán; Benjamin, Simon C.; Yuan, Xiao (30 de marzo de 2020). "Química computacional cuántica". Reseñas de Física Moderna . 92 (1): 015003. arXiv : 1808.10402 . Código Bibliográfico :2020RvMP...92a5003M. doi : 10.1103/RevModPhys.92.015003 . ISSN  0034-6861.
  73. ^ Bignon, Emmanuelle; Monari, Antonio (1 de enero de 2024). "Dinámica molecular y QM/MM para comprender la organización y reproducción del genoma en virus ARN emergentes". Química computacional integral : 895–909. doi :10.1016/B978-0-12-821978-2.00101-X. ISBN 978-0-12-823256-9. Número de identificación del sujeto  258397837.
  74. ^ Abrams, Daniel S.; Lloyd, Seth (13 de diciembre de 1999). "Algoritmo cuántico que proporciona un aumento exponencial de la velocidad para hallar valores propios y vectores propios". Physical Review Letters . 83 (24): 5162–5165. arXiv : quant-ph/9807070 . Código Bibliográfico :1999PhRvL..83.5162A. doi :10.1103/PhysRevLett.83.5162. S2CID  118937256.
  75. ^ Feynman, Richard P. (17 de junio de 2019). Hola, Tony; Allen, Robin W. (eds.). Feynman Lectures On Computation. Boca Raton: CRC Press. doi :10.1201/9780429500442. ISBN 978-0-429-50044-2.S2CID53898623  .​
  76. ^ de Nielsen, Michael A.; Chuang, Isaac L. (2010). Computación cuántica e información cuántica (edición del décimo aniversario). Cambridge: Cambridge University Press. ISBN 978-1-107-00217-3.
  77. ^ McArdle, Sam; Endo, Suguru; Aspuru-Guzik, Alán; Benjamin, Simon C.; Yuan, Xiao (30 de marzo de 2020). "Química computacional cuántica". Reseñas de Física Moderna . 92 (1): 015003. arXiv : 1808.10402 . Código Bibliográfico :2020RvMP...92a5003M. doi : 10.1103/RevModPhys.92.015003 .
  78. ^ Jäger, Jonas; Krems, Roman V. (2 de febrero de 2023). "Expresividad universal de clasificadores cuánticos variacionales y núcleos cuánticos para máquinas de vectores de soporte". Nature Communications . 14 (1). Nature: 576. arXiv : 2207.05865 . Bibcode :2023NatCo..14..576J. doi :10.1038/s41467-023-36144-5. ISSN  2041-1723. PMC 9895068 . PMID  36732519. 
  79. ^ Teoría de la estructura electrónica moderna. 1 . Serie avanzada en química física. Singapur: World Scientific. 1995. ISBN 978-981-02-2987-0.
  80. ^ Adcock, Stewart A.; McCammon, J. Andrew (1 de mayo de 2006). "Dinámica molecular: estudio de métodos para simular la actividad de las proteínas". Chemical Reviews . 106 (5): 1589–1615. doi :10.1021/cr040426m. ISSN  0009-2665. PMC 2547409 . PMID  16683746. 
  81. ^ Durrant, Jacob D.; McCammon, J. Andrew (28 de octubre de 2011). "Simulaciones de dinámica molecular y descubrimiento de fármacos". BMC Biology . 9 (1): 71. doi : 10.1186/1741-7007-9-71 . ISSN  1741-7007. PMC 3203851 . PMID  22035460. 
  82. ^ Stephan, Simon; Horsch, Martin T.; Vrabec, Jadran; Hasse, Hans (3 de julio de 2019). "MolMod: una base de datos de acceso abierto de campos de fuerza para simulaciones moleculares de fluidos". Molecular Simulation . 45 (10): 806–814. arXiv : 1904.05206 . doi :10.1080/08927022.2019.1601191. ISSN  0892-7022. S2CID  119199372.
  83. ^ Kurzak, J.; Pettitt, BM (septiembre de 2006). "Métodos multipolares rápidos para dinámica de partículas". Molecular Simulation . 32 (10–11): 775–790. doi :10.1080/08927020600991161. ISSN  0892-7022. PMC 2634295 . PMID  19194526. 
  84. ^ Giese, Timothy J.; Panteva, Maria T.; Chen, Haoyuan; York, Darrin M. (10 de febrero de 2015). "Métodos multipolares de Ewald, 1: teoría, precisión y rendimiento". Revista de teoría y computación química . 11 (2): 436–450. doi :10.1021/ct5007983. ISSN  1549-9618. PMC 4325605 . PMID  25691829. 
  85. ^ Groenhof, Gerrit (2013), Monticelli, Luca; Salonen, Emppu (eds.), "Introducción a las simulaciones QM/MM", Simulaciones biomoleculares: métodos y protocolos , Métodos en biología molecular, vol. 924, Totowa, NJ: Humana Press, págs. 43–66, doi :10.1007/978-1-62703-017-5_3, hdl : 11858/00-001M-0000-0010-15DF-C , ISBN 978-1-62703-017-5, PMID23034745 ​
  86. ^ Tzeliou, Christina Eleftheria; Mermigki, Markella Aliki; Tzeli, Demeter (enero de 2022). "Revisión de las metodologías QM/MM y su aplicación a las metaloproteínas". Moléculas . 27 (9): 2660. doi : 10.3390/molecules27092660 . ISSN  1420-3049. PMC 9105939 . PMID  35566011. 
  87. ^ ab Lucas, Andrew (2014). "Formulaciones de Ising de muchos problemas NP". Frontiers in Physics . 2 : 5. arXiv : 1302.5843 . Bibcode :2014FrP.....2....5L. doi : 10.3389/fphy.2014.00005 . ISSN  2296-424X.
  88. ^ Rastegar, Somayeh F.; Hadipour, Nasser L.; Tabar, Mohammad Bigdeli; Soleymanabadi, Hamed (1 de septiembre de 2013). "Estudios DFT de la adsorción de moléculas de acroleína en grafenos prístinos y dopados con Al". Journal of Molecular Modeling . 19 (9): 3733–3740. doi :10.1007/s00894-013-1898-5. ISSN  1610-2940. PMID  23793719. S2CID  41375235.
  89. ^ Kohn, W.; Sham, LJ (15 de noviembre de 1965). "Ecuaciones autoconsistentes que incluyen efectos de intercambio y correlación". Physical Review . 140 (4A): A1133–A1138. Código Bibliográfico :1965PhRv..140.1133K. doi : 10.1103/PhysRev.140.A1133 .
  90. ^ Michaud-Rioux, Vincent; Zhang, Lei; Guo, Hong (15 de febrero de 2016). "RESCU: Un método de estructura electrónica espacial real". Journal of Computational Physics . 307 : 593–613. arXiv : 1509.05746 . Código Bibliográfico :2016JCoPh.307..593M. doi :10.1016/j.jcp.2015.12.014. ISSN  0021-9991. S2CID  28836129.
  91. ^ Motamarri, Phani; Das, Sambit; Rudraraju, Shiva; Ghosh, Krishnendu; Davydov, Denis; Gavini, Vikram (1 de enero de 2020). "DFT-FE: un código de elementos finitos adaptativo masivamente paralelo para cálculos de teoría funcional de densidad a gran escala". Comunicaciones de Física Informática . 246 : 106853. arXiv : 1903.10959 . Código Bib : 2020CoPhC.24606853M. doi :10.1016/j.cpc.2019.07.016. ISSN  0010-4655. S2CID  85517990.
  92. ^ abcdef Sengupta, Arkajyoti; Ramabhadran, Raghunath O.; Raghavachari, Krishnan (15 de enero de 2016). "Rompiendo un cuello de botella: extrapolación precisa a energías CCSD(T) de "estándar de oro" para radicales orgánicos de capa abierta grandes a un costo computacional reducido". Journal of Computational Chemistry . 37 (2): 286–295. doi :10.1002/jcc.24050. ISSN  0192-8651. PMID  26280676. S2CID  23011794.
  93. ^ ab Whitfield, James Daniel; Love, Peter John; Aspuru-Guzik, Alán (2013). "Complejidad computacional en la estructura electrónica". Phys. Chem. Chem. Phys . 15 (2): 397–411. arXiv : 1208.3334 . Bibcode :2013PCCP...15..397W. doi :10.1039/C2CP42695A. ISSN  1463-9076. PMID  23172634. S2CID  12351374.
  94. ^ Desafíos matemáticos de la química teórica y computacional. Washington, DC: National Academies Press. 29 de marzo de 1995. doi :10.17226/4886. ISBN 978-0-309-05097-5.
  95. ^ Visscher, Lucas (junio de 2002). "La ecuación de Dirac en química cuántica: estrategias para superar los problemas computacionales actuales". Journal of Computational Chemistry . 23 (8): 759–766. doi :10.1002/jcc.10036. ISSN  0192-8651. PMID  12012352. S2CID  19427995.
  96. ^ Sax, Alexander F. (1 de abril de 2008). "Técnicas de química computacional: abarcando órdenes de magnitud en el espacio, el tiempo y la precisión". Revista de química - Chemical Monthly . 139 (4): 299–308. doi :10.1007/s00706-007-0827-7. ISSN  1434-4475. S2CID  85451980.
  97. ^ Friesner, R. (1 de marzo de 2003). "Cómo las proteínas que contienen hierro controlan la química del dioxígeno: una descripción detallada a nivel atómico mediante cálculos precisos de química cuántica y mecánica cuántica/mecánica molecular". Coordination Chemistry Reviews . 238–239: 267–290. doi :10.1016/S0010-8545(02)00284-9. ISSN  0010-8545.