
En matemáticas , una parábola es una curva plana con simetría especular y con forma aproximada de U. Se ajusta a varias descripciones matemáticas superficialmente diferentes , que pueden demostrar que definen exactamente las mismas curvas.
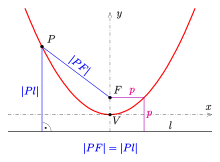
Una descripción de una parábola implica un punto (el foco ) y una línea (la directriz ). El foco no se encuentra en la directriz. La parábola es el lugar geométrico de los puntos en ese plano que son equidistantes de la directriz y el foco. Otra descripción de una parábola es como una sección cónica , creada a partir de la intersección de una superficie cónica circular recta y un plano paralelo a otro plano que es tangente a la superficie cónica. [a]
La gráfica de una función cuadrática (con ) es una parábola cuyo eje es paralelo al eje y . A la inversa, cada una de estas parábolas es la gráfica de una función cuadrática.
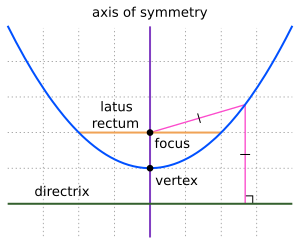
La línea perpendicular a la directriz y que pasa por el foco (es decir, la línea que divide la parábola por la mitad) se llama "eje de simetría". El punto donde la parábola interseca su eje de simetría se llama " vértice " y es el punto donde la parábola está más curvada. La distancia entre el vértice y el foco, medida a lo largo del eje de simetría, es la "distancia focal". El " latus rectum " es la cuerda de la parábola que es paralela a la directriz y pasa por el foco. Las parábolas pueden abrirse hacia arriba, hacia abajo, hacia la izquierda, hacia la derecha o en alguna otra dirección arbitraria. Cualquier parábola se puede reposicionar y reescalar para que encaje exactamente en cualquier otra parábola, es decir, todas las parábolas son geométricamente similares .
Las parábolas tienen la propiedad de que, si están hechas de un material que refleja la luz , entonces la luz que viaja paralela al eje de simetría de una parábola e incide en su lado cóncavo se refleja en su foco, independientemente de en qué parte de la parábola se produzca la reflexión. Por el contrario, la luz que se origina en una fuente puntual en el foco se refleja en un haz paralelo (" colimado "), dejando la parábola paralela al eje de simetría. Los mismos efectos ocurren con el sonido y otras ondas . Esta propiedad reflectante es la base de muchos usos prácticos de las parábolas.
La parábola tiene muchas aplicaciones importantes, desde una antena parabólica o un micrófono parabólico hasta reflectores de faros de automóviles y el diseño de misiles balísticos . Se utiliza con frecuencia en física , ingeniería y muchas otras áreas.

El trabajo más antiguo conocido sobre secciones cónicas fue realizado por Menecmo en el siglo IV a. C. Descubrió una forma de resolver el problema de doblar el cubo usando parábolas. (La solución, sin embargo, no cumple con los requisitos de la construcción con regla y compás ). El área encerrada por una parábola y un segmento de línea, el llamado "segmento de parábola", fue calculada por Arquímedes por el método de exhaución en el siglo III a. C., en su Cuadratura de la parábola . El nombre "parábola" se debe a Apolonio , quien descubrió muchas propiedades de las secciones cónicas. Significa "aplicación", refiriéndose al concepto de "aplicación de áreas", que tiene una conexión con esta curva, como Apolonio había demostrado. [1] La propiedad foco-directriz de la parábola y otras secciones cónicas se debe a Pappus .
Galileo demostró que la trayectoria de un proyectil sigue una parábola, consecuencia de la aceleración uniforme debida a la gravedad.
La idea de que un reflector parabólico podía producir una imagen ya era bien conocida antes de la invención del telescopio reflector . [2] Muchos matemáticos propusieron diseños a principios y mediados del siglo XVII , entre ellos René Descartes , Marin Mersenne , [3] y James Gregory . [4] Cuando Isaac Newton construyó el primer telescopio reflector en 1668, omitió el uso de un espejo parabólico debido a la dificultad de fabricación, optando por un espejo esférico . Los espejos parabólicos se utilizan en la mayoría de los telescopios reflectores modernos y en antenas parabólicas y receptores de radar . [5]
Una parábola se puede definir geométricamente como un conjunto de puntos ( lugar geométrico de puntos ) en el plano euclidiano:
El punto medio de la perpendicular desde el foco hasta la directriz se llama vértice y la línea es el eje de simetría de la parábola.
Si se introducen coordenadas cartesianas , tales que y la directriz tiene la ecuación , se obtiene para un punto de la ecuación . Resolviendo para se obtiene
Esta parábola tiene forma de U ( se abre hacia arriba ).
La cuerda horizontal que pasa por el foco (ver la imagen en la sección inicial) se llama lado recto ; una mitad de ella es el semilato recto . El lado recto es paralelo a la directriz. El semilato recto se designa con la letra . De la imagen se obtiene
El lado recto se define de manera similar para las otras dos cónicas: la elipse y la hipérbola. El lado recto es la línea trazada a través de un foco de una sección cónica paralela a la directriz y terminada en ambos sentidos por la curva. Para cualquier caso, es el radio del círculo osculador en el vértice. Para una parábola, el semilado recto, , es la distancia del foco a la directriz. Usando el parámetro , la ecuación de la parábola puede reescribirse como
De manera más general, si el vértice es , el foco y la directriz , se obtiene la ecuación
Observaciones :

Si el foco es , y la directriz , entonces se obtiene la ecuación
(el lado izquierdo de la ecuación utiliza la forma normal de Hesse de una línea para calcular la distancia ).
Para una ecuación paramétrica de una parábola en posición general, véase § Como imagen afín de la parábola unitaria.
La ecuación implícita de una parábola está definida por un polinomio irreducible de grado dos: tal que o, equivalentemente, tal que es el cuadrado de un polinomio lineal .

La sección anterior muestra que cualquier parábola con el origen como vértice y el eje y como eje de simetría puede considerarse como la gráfica de una función.
Las parábolas se abren hacia arriba y las parábolas se abren hacia abajo (ver figura). De la sección anterior se obtiene:
La parábola es la parábola unitaria de ecuación . Su foco es , el semilato recto , y la directriz tiene ecuación .
La función general de grado 2 es Completar el cuadrado da como resultado la ecuación de una parábola con

Dos objetos en el plano euclidiano son semejantes si uno puede transformarse en el otro mediante una semejanza , es decir, una composición arbitraria de movimientos rígidos ( traslaciones y rotaciones ) y escalas uniformes .
Una parábola con vértice puede transformarse mediante la traslación en una que tenga el origen como vértice. Una rotación adecuada alrededor del origen puede transformar la parábola en una que tenga el eje y como eje de simetría. Por lo tanto, la parábola puede transformarse mediante un movimiento rígido en una parábola con una ecuación . Dicha parábola puede luego transformarse mediante el escalado uniforme en la parábola unitaria con ecuación . Por lo tanto, cualquier parábola puede mapearse a la parábola unitaria por una semejanza. [6]
También se puede utilizar un enfoque sintético , utilizando triángulos similares, para establecer este resultado. [7]
El resultado general es que dos secciones cónicas (necesariamente del mismo tipo) son similares si y solo si tienen la misma excentricidad. [6] Por lo tanto, solo los círculos (todos con excentricidad 0) comparten esta propiedad con las parábolas (todas con excentricidad 1), mientras que las elipses generales y las hipérbolas no.
Existen otras transformaciones afines simples que asignan la parábola a la parábola unitaria, como . Pero esta asignación no es una semejanza, y solo muestra que todas las parábolas son afínmente equivalentes (véase § Como la imagen afín de la parábola unitaria).

El lápiz de secciones cónicas con eje x como eje de simetría, un vértice en el origen (0, 0) y el mismo semilato recto se puede representar mediante la ecuación con excentricidad .

Si p > 0 , la parábola con ecuación (apertura hacia la derecha) tiene la representación polar donde .
Su vértice es y su foco es .
Si se desplaza el origen hacia el foco, es decir, se obtiene la ecuación
Observación 1: Invertir esta forma polar muestra que una parábola es la inversa de un cardioide .
Observación 2: La segunda forma polar es un caso especial de un lápiz de cónicas con foco (ver imagen): ( es la excentricidad).

El diagrama representa un cono cuyo eje es AV . El punto A es su vértice . Una sección transversal inclinada del cono, que se muestra en rosa, está inclinada respecto del eje en el mismo ángulo θ que el lado del cono. Según la definición de parábola como sección cónica, el límite de esta sección transversal rosa EPD es una parábola.
Por el vértice P de la parábola pasa una sección transversal perpendicular al eje del cono. Esta sección transversal es circular, pero vista oblicuamente parece elíptica , como se muestra en el diagrama. Su centro es V y PK es un diámetro. Llamaremos a su radio r .
Otra sección transversal circular perpendicular al eje del cono está más alejada del vértice A que la que acabamos de describir. Tiene una cuerda DE que une los puntos donde la parábola corta al círculo. Otra cuerda BC es la mediatriz de DE y, en consecuencia, un diámetro del círculo. Estas dos cuerdas y el eje de simetría de la parábola PM se cortan en el punto M.
Todos los puntos marcados, excepto D y E, son coplanares . Están en el plano de simetría de toda la figura. Esto incluye el punto F, que no se menciona arriba. Se define y analiza más adelante, en § Posición del foco.
Llamemos a la longitud de DM y de EM x , y a la longitud de PM y .
Las longitudes de BM y CM son:
Utilizando el teorema de las cuerdas que se intersectan en las cuerdas BC y DE , obtenemos
Sustituyendo:
Reorganizando:
Para cualquier cono y parábola dados, r y θ son constantes, pero x e y son variables que dependen de la altura arbitraria a la que se realiza la sección transversal horizontal BECD. Esta última ecuación muestra la relación entre estas variables. Pueden interpretarse como coordenadas cartesianas de los puntos D y E, en un sistema en el plano rosa con P como origen. Como x está elevado al cuadrado en la ecuación, el hecho de que D y E estén en lados opuestos del eje y no es importante. Si la sección transversal horizontal se mueve hacia arriba o hacia abajo, acercándose o alejándose del vértice del cono, D y E se mueven a lo largo de la parábola, manteniendo siempre la relación entre x e y mostrada en la ecuación. La curva parabólica es, por lo tanto, el lugar geométrico de los puntos donde se satisface la ecuación, lo que la convierte en un gráfico cartesiano de la función cuadrática en la ecuación.
Se demuestra en una sección anterior que si una parábola tiene su vértice en el origen y se abre en la dirección y positiva, entonces su ecuación es y = x2/4f , donde f es su longitud focal. [b] Comparando esto con la última ecuación anterior se muestra que la longitud focal de la parábola en el cono es r sen θ .
En el diagrama anterior, el punto V es el pie de la perpendicular desde el vértice de la parábola hasta el eje del cono. El punto F es el pie de la perpendicular desde el punto V hasta el plano de la parábola. [c] Por simetría, F está en el eje de simetría de la parábola. El ángulo VPF es complementario de θ , y el ángulo PVF es complementario del ángulo VPF, por lo tanto, el ángulo PVF es θ . Como la longitud de PV es r , la distancia de F desde el vértice de la parábola es r sen θ . Se muestra arriba que esta distancia es igual a la longitud focal de la parábola, que es la distancia desde el vértice hasta el foco. El foco y el punto F están, por lo tanto, igualmente distantes del vértice, a lo largo de la misma línea, lo que implica que son el mismo punto. Por lo tanto, el punto F, definido arriba, es el foco de la parábola .
Esta discusión comenzó con la definición de una parábola como una sección cónica, pero ahora ha conducido a una descripción como un gráfico de una función cuadrática. Esto demuestra que estas dos descripciones son equivalentes. Ambas definen curvas con exactamente la misma forma.
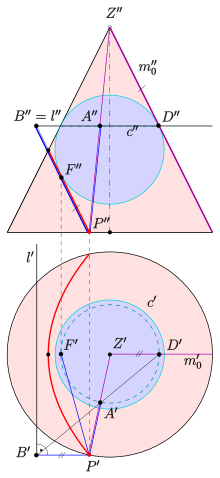
Se puede hacer una prueba alternativa utilizando esferas de Dandelin . Funciona sin cálculos y utiliza únicamente consideraciones geométricas elementales (ver la derivación a continuación).
La intersección de un cono vertical con un plano , cuya inclinación respecto de la vertical es la misma que la generatriz (también conocida como línea generadora, una línea que contiene el vértice y un punto en la superficie del cono) del cono, es una parábola (curva roja en el diagrama).
Esta generatriz es la única generatriz del cono que es paralela al plano . De lo contrario, si hay dos generatrices paralelas al plano de intersección, la curva de intersección será una hipérbola (o hipérbola degenerada , si las dos generatrices están en el plano de intersección). Si no hay ninguna generatriz paralela al plano de intersección, la curva de intersección será una elipse o un círculo (o un punto ).
Sea plano el plano que contiene el eje vertical del cono y la recta . La inclinación del plano respecto de la vertical es la misma que la de la recta, lo que significa que, viéndolo de lado (es decir, el plano es perpendicular al plano ), .
Para demostrar la propiedad directriz de una parábola (ver § Definición como lugar geométrico de puntos arriba), se utiliza una esfera de Dandelin , que es una esfera que toca al cono a lo largo de un círculo y un plano en el punto . El plano que contiene al círculo interseca al plano en la línea . Existe una simetría especular en el sistema que consta del plano , la esfera de Dandelin y el cono (el plano de simetría es ).
Como el plano que contiene el círculo es perpendicular al plano , y , su línea de intersección también debe ser perpendicular al plano . Como la línea está en el plano , .
Resulta que es el foco de la parábola, y es la directriz de la parábola.

La propiedad de reflexión establece que si una parábola puede reflejar la luz, entonces la luz que entra en ella viajando paralela al eje de simetría se refleja hacia el foco. Esto se deriva de la óptica geométrica , basada en el supuesto de que la luz viaja en rayos.
Considere la parábola y = x 2 . Como todas las parábolas son similares, este caso simple representa a todas las demás.
El punto E es un punto arbitrario de la parábola. El foco es F, el vértice es A (el origen) y la línea FA es el eje de simetría. La línea EC es paralela al eje de simetría, interseca el eje x en D e interseca la directriz en C. El punto B es el punto medio del segmento FC .
El vértice A es equidistante del foco F y de la directriz. Como C está sobre la directriz, las coordenadas y de F y C son iguales en valor absoluto y opuestas en signo. B es el punto medio de FC . Su coordenada x es la mitad de la de D, es decir, x /2 . La pendiente de la recta BE es el cociente de las longitudes de ED y BD , que es x2/x /2 = 2 x . Pero 2 x es también la pendiente (primera derivada) de la parábola en E. Por lo tanto, la línea BE es la tangente a la parábola en E.
Las distancias EF y EC son iguales porque E está en la parábola, F es el foco y C está en la directriz. Por lo tanto, como B es el punto medio de FC , los triángulos △FEB y △CEB son congruentes (tres lados), lo que implica que los ángulos marcados con α son congruentes. (El ángulo sobre E es el ángulo verticalmente opuesto ∠BEC). Esto significa que un rayo de luz que entra en la parábola y llega a E viajando paralelo al eje de simetría será reflejado por la línea BE, por lo que viaja a lo largo de la línea EF , como se muestra en rojo en el diagrama (asumiendo que las líneas pueden reflejar la luz de alguna manera). Como BE es la tangente a la parábola en E, la misma reflexión será realizada por un arco infinitesimal de la parábola en E. Por lo tanto, la luz que entra en la parábola y llega a E viajando paralela al eje de simetría de la parábola es reflejada por la parábola hacia su foco.
Esta conclusión sobre la luz reflejada se aplica a todos los puntos de la parábola, como se muestra en el lado izquierdo del diagrama. Esta es la propiedad de reflexión.
Hay otros teoremas que pueden deducirse simplemente del argumento anterior.
La prueba anterior y el diagrama que la acompaña muestran que la tangente BE biseca el ángulo ∠FEC. En otras palabras, la tangente a la parábola en cualquier punto biseca el ángulo entre las líneas que unen el punto con el foco y perpendicularmente a la directriz.

Como los triángulos △FBE y △CBE son congruentes, FB es perpendicular a la tangente BE . Como B está en el eje x , que es la tangente a la parábola en su vértice, se deduce que el punto de intersección entre cualquier tangente a una parábola y la perpendicular desde el foco a esa tangente se encuentra en la línea que es tangente a la parábola en su vértice. Véase el diagrama animado [8] y la curva pedal .
Si la luz viaja a lo largo de la línea CE , se mueve paralela al eje de simetría y golpea el lado convexo de la parábola en E. Del diagrama anterior se desprende claramente que esta luz se reflejará directamente lejos del foco, a lo largo de una extensión del segmento FE .
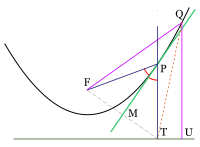
Las demostraciones anteriores de las propiedades de reflexión y bisección tangente utilizan una línea de cálculo. Aquí se presenta una demostración geométrica.
En este diagrama, F es el foco de la parábola, y T y U se encuentran en su directriz. P es un punto arbitrario en la parábola. PT es perpendicular a la directriz, y la línea MP biseca el ángulo ∠FPT. Q es otro punto en la parábola, con QU perpendicular a la directriz. Sabemos que FP = PT y FQ = QU . Claramente, QT > QU , por lo que QT > FQ . Todos los puntos en la bisectriz MP son equidistantes de F y T, pero Q está más cerca de F que de T. Esto significa que Q está a la izquierda de MP , es decir, en el mismo lado que el foco. Lo mismo sería cierto si Q estuviera ubicado en cualquier otro lugar de la parábola (excepto en el punto P), por lo que toda la parábola, excepto el punto P, está en el lado del foco de MP . Por lo tanto, MP es la tangente a la parábola en P. Dado que biseca el ángulo ∠FPT, esto demuestra la propiedad de bisección de la tangente.
La lógica del último párrafo se puede aplicar para modificar la prueba anterior de la propiedad reflexiva. Demuestra efectivamente que la línea BE es la tangente a la parábola en E si los ángulos α son iguales. La propiedad reflexiva se deduce como se mostró anteriormente.
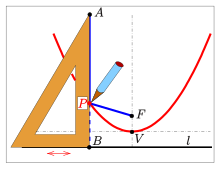
La definición de una parábola por su foco y directriz se puede utilizar para dibujarla con ayuda de alfileres y cuerdas: [9]
Una parábola puede considerarse como la parte afín de una cónica proyectiva no degenerada con un punto en la línea del infinito , que es la tangente en . Las degeneraciones de 5, 4 y 3 puntos del teorema de Pascal son propiedades de una cónica que trata con al menos una tangente. Si se considera esta tangente como la línea en el infinito y su punto de contacto como el punto en el infinito del eje y , se obtienen tres afirmaciones para una parábola.
Las siguientes propiedades de una parábola se refieren únicamente a los términos conexos , intersecantes y paralelos , que son invariantes de semejanzas . Por lo tanto, es suficiente demostrar cualquier propiedad para la parábola unitaria con ecuación .

Cualquier parábola puede describirse en un sistema de coordenadas adecuado mediante una ecuación .
Demostración: cálculo sencillo para la parábola unitaria .
Aplicación: La propiedad de los 4 puntos de una parábola se puede utilizar para la construcción del punto , mientras que y se dan.
Observación: la propiedad de 4 puntos de una parábola es una versión afín de la degeneración de 5 puntos del teorema de Pascal.
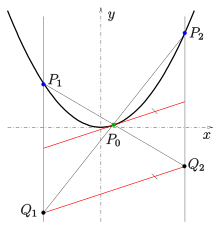
Sean tres puntos de la parábola con ecuación y la intersección de la recta secante con la recta y la intersección de la recta secante con la recta (ver figura). Entonces la tangente en el punto es paralela a la recta . (Las rectas y son paralelas al eje de la parábola).
Demostración: se puede realizar para la parábola unitaria . Un cálculo breve muestra: la pendiente de la recta es la pendiente de la tangente en el punto .
Aplicación: La propiedad 3-puntos-1-tangente de una parábola se puede utilizar para la construcción de la tangente en el punto , mientras se dan.
Observación: La propiedad de tangente de 3 puntos y 1 de una parábola es una versión afín de la degeneración de 4 puntos del teorema de Pascal.
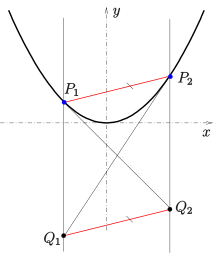
Sean dos puntos de la parábola con ecuación , y la intersección de la tangente en el punto con la recta , y la intersección de la tangente en el punto con la recta (ver figura). Entonces la secante es paralela a la recta . (Las rectas y son paralelas al eje de la parábola).
Demostración: cálculo sencillo para la parábola unitaria .
Aplicación: La propiedad 2-puntos-2-tangentes se puede utilizar para la construcción de la tangente de una parábola en el punto , si y la tangente en están dadas.
Observación 1: La propiedad de 2 puntos-2 tangentes de una parábola es una versión afín de la degeneración de 3 puntos del teorema de Pascal.
Observación 2: La propiedad de 2 puntos y 2 tangentes no debe confundirse con la siguiente propiedad de una parábola, que también trata con 2 puntos y 2 tangentes, pero no está relacionada con el teorema de Pascal.

Las afirmaciones anteriores presuponen el conocimiento de la dirección del eje de la parábola para construir los puntos . La siguiente propiedad determina los puntos a partir de dos puntos dados y sus tangentes únicamente, y el resultado es que la línea es paralela al eje de la parábola.
Dejar
Entonces la recta es paralela al eje de la parábola y tiene la ecuación
Demostración: se puede hacer (como las propiedades anteriores) para la parábola unitaria .
Aplicación: Esta propiedad se puede utilizar para determinar la dirección del eje de una parábola, si se dan dos puntos y sus tangentes. Una forma alternativa es determinar los puntos medios de dos cuerdas paralelas, consulte la sección sobre cuerdas paralelas.
Observación: Esta propiedad es una versión afín del teorema de dos triángulos en perspectiva de una cónica no degenerada. [10]
Steiner estableció el siguiente procedimiento para la construcción de una cónica no degenerada (ver cónica de Steiner ):
Este procedimiento se puede utilizar para una construcción simple de puntos en la parábola :
Prueba: cálculo sencillo.
Observación: La generación de Steiner también está disponible para elipses e hipérbolas .
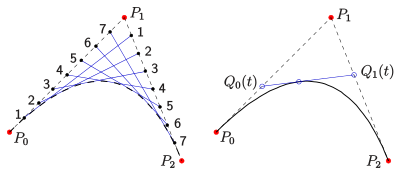
Una parábola dual consiste en el conjunto de tangentes de una parábola ordinaria.
La generación de Steiner de una cónica se puede aplicar a la generación de una cónica dual cambiando los significados de los puntos y las líneas:
Para generar elementos de una parábola dual, se comienza con
La prueba es una consecuencia del algoritmo de Casteljau para una curva de Bézier de grado 2.
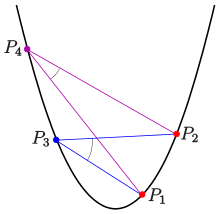
Una parábola con ecuación está determinada de forma única por tres puntos con coordenadas x diferentes . El procedimiento habitual para determinar los coeficientes es insertar las coordenadas de los puntos en la ecuación. El resultado es un sistema lineal de tres ecuaciones, que se puede resolver mediante la eliminación gaussiana o la regla de Cramer , por ejemplo. Una forma alternativa utiliza el teorema del ángulo inscrito para las parábolas.
A continuación, se medirá el ángulo de dos rectas por la diferencia de las pendientes de la recta respecto a la directriz de la parábola. Es decir, para una parábola de ecuación el ángulo entre dos rectas de ecuaciones se mide por
De manera análoga al teorema del ángulo inscrito para círculos, se tiene el teorema del ángulo inscrito para parábolas : [11] [12]
(Demostración: cálculo sencillo: si los puntos están en una parábola, se pueden traducir las coordenadas para tener la ecuación , entonces se tiene si los puntos están en la parábola).
Una consecuencia es que la ecuación (en ) de la parábola determinada por 3 puntos con diferentes coordenadas x es (si dos coordenadas x son iguales, no existe parábola con directriz paralela al eje x , que pase por los puntos) Multiplicando por los denominadores que dependen de uno se obtiene la forma más estándar
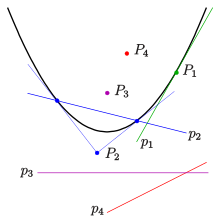
En un sistema de coordenadas adecuado, cualquier parábola puede describirse mediante una ecuación . La ecuación de la tangente en un punto es Se obtiene la función sobre el conjunto de puntos de la parábola sobre el conjunto de tangentes.
Obviamente, esta función se puede extender al conjunto de todos los puntos de hasta una biyección entre los puntos de y las rectas con ecuaciones . La aplicación inversa es Esta relación se llama relación polo-polar de la parábola , donde el punto es el polo y la recta correspondiente su polar .
Mediante el cálculo se comprueban las siguientes propiedades de la relación polo-polar de la parábola:
Observación: También existen relaciones polo-polar para elipses e hipérbolas.
Sea la línea de simetría la que interseca la parábola en el punto Q, y denotemos el foco como punto F y su distancia al punto Q como f . Sea la perpendicular a la línea de simetría, que pasa por el foco, la que interseca la parábola en un punto T. Entonces (1) la distancia de F a T es 2 f , y (2) una tangente a la parábola en el punto T interseca la línea de simetría en un ángulo de 45°. [13] : 26
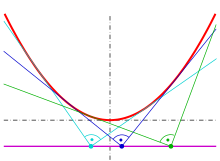
Si dos tangentes a una parábola son perpendiculares entre sí, entonces se cortan en la directriz. A la inversa, dos tangentes que se cortan en la directriz son perpendiculares. En otras palabras, en cualquier punto de la directriz toda la parábola subtiende un ángulo recto.
Supongamos que tres tangentes a una parábola forman un triángulo. Entonces, el teorema de Lambert establece que el foco de la parábola se encuentra en la circunferencia circunscrita al triángulo. [14] [8] : Corolario 20
El recíproco de Tsukerman al teorema de Lambert establece que, dadas tres líneas que delimitan un triángulo, si dos de las líneas son tangentes a una parábola cuyo foco se encuentra en el círculo circunscrito del triángulo, entonces la tercera línea también es tangente a la parábola. [15]
Supongamos que una cuerda corta una parábola perpendicular a su eje de simetría. Sea c la longitud de la cuerda entre los puntos donde corta la parábola y d la distancia desde el vértice de la parábola hasta la cuerda, medida a lo largo del eje de simetría . La distancia focal, f , de la parábola está dada por
Supongamos que se utiliza un sistema de coordenadas cartesianas de modo que el vértice de la parábola está en el origen y el eje de simetría es el eje y . La parábola se abre hacia arriba. En otra parte de este artículo se muestra que la ecuación de la parábola es 4 fy = x 2 , donde f es la distancia focal. En el extremo x positivo de la cuerda, x = do/2 y y = d . Como este punto está en la parábola, estas coordenadas deben satisfacer la ecuación anterior. Por lo tanto, por sustitución,. A partir de esto,.
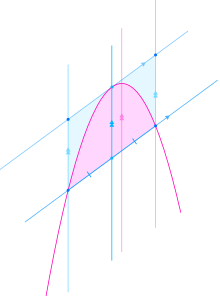
El área encerrada entre una parábola y una cuerda (ver diagrama) es dos tercios del área de un paralelogramo que la rodea. Un lado del paralelogramo es la cuerda y el lado opuesto es una tangente a la parábola. [16] [17] La pendiente de los otros lados paralelos es irrelevante para el área. A menudo, como aquí, se dibujan paralelos al eje de simetría de la parábola, pero esto es arbitrario.
En el siglo III a. C., Arquímedes dedujo un teorema equivalente a éste, pero diferente en detalles . Utilizó las áreas de los triángulos, en lugar de las del paralelogramo. [d] Véase La cuadratura de la parábola .
Si la cuerda tiene una longitud b y es perpendicular al eje de simetría de la parábola, y si la distancia perpendicular desde el vértice de la parábola hasta la cuerda es h , el paralelogramo es un rectángulo, con lados b y h . El área A del segmento parabólico encerrado por la parábola y la cuerda es, por lo tanto,
Esta fórmula se puede comparar con el área de un triángulo :1/2 bh .
En general, el área encerrada se puede calcular de la siguiente manera. Primero, localiza el punto en la parábola donde su pendiente es igual a la de la cuerda. Esto se puede hacer con cálculo, o usando una línea que sea paralela al eje de simetría de la parábola y pase por el punto medio de la cuerda. El punto requerido es donde esta línea interseca la parábola. [e] Luego, usando la fórmula dada en Distancia de un punto a una línea , calcula la distancia perpendicular desde este punto a la cuerda. Multiplica esto por la longitud de la cuerda para obtener el área del paralelogramo, luego por 2/3 para obtener el área encerrada requerida.

Un corolario de la discusión anterior es que si una parábola tiene varias cuerdas paralelas, sus puntos medios se encuentran todos en una línea paralela al eje de simetría. Si se trazan tangentes a la parábola a través de los puntos finales de cualquiera de estas cuerdas, las dos tangentes se intersecan en esta misma línea paralela al eje de simetría (véase Dirección del eje de una parábola). [f]
Si un punto X está ubicado en una parábola con longitud focal f , y si p es la distancia perpendicular de X al eje de simetría de la parábola, entonces las longitudes de los arcos de la parábola que terminan en X se pueden calcular a partir de f y p de la siguiente manera, asumiendo que todos están expresados en las mismas unidades. [g]
Esta cantidad s es la longitud del arco entre X y el vértice de la parábola.
La longitud del arco entre X y el punto simétricamente opuesto en el otro lado de la parábola es 2 s .
La distancia perpendicular p puede tener un signo positivo o negativo para indicar en qué lado del eje de simetría se encuentra X. Al invertir el signo de p se invierten los signos de h y s sin cambiar sus valores absolutos. Si estas cantidades tienen signo, la longitud del arco entre dos puntos cualesquiera de la parábola siempre se muestra por la diferencia entre sus valores de s . El cálculo se puede simplificar utilizando las propiedades de los logaritmos:
Esto puede ser útil, por ejemplo, para calcular el tamaño del material necesario para fabricar un reflector parabólico o un canal parabólico .
Este cálculo se puede utilizar para una parábola en cualquier orientación. No se limita a la situación en la que el eje de simetría es paralelo al eje y .
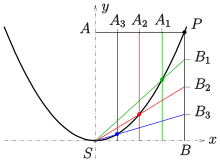
S es el foco y V es el vértice principal de la parábola VG. Dibuje VX perpendicular a SV.
Tomar cualquier punto B en VG y trazar una perpendicular BQ desde B hasta VX. Trazar la perpendicular ST que interseca a BQ, prolongada si es necesario, en T. En B trazar la perpendicular BJ, que interseca a VX en J.
Para la parábola, el segmento VBV, el área encerrada por la cuerda VB y el arco VB, es igual a ∆VBQ / 3, también .
El área del sector parabólico .
Como los triángulos TSB y QBJ son similares,
Por lo tanto, el área del sector parabólico y se puede encontrar a partir de la longitud de VJ, como se encontró arriba.
Un círculo que pasa por S, V y B también pasa por J.
Por el contrario, si se busca un punto B en la parábola VG de modo que el área del sector SVB sea igual a un valor especificado, se determina el punto J en VX y se construye un círculo a través de S, V y J. Como SJ es el diámetro, el centro del círculo está en su punto medio y se encuentra en la bisectriz perpendicular de SV, a una distancia de la mitad de VJ de SV. El punto B buscado es donde este círculo interseca la parábola.
Si un cuerpo sigue la trayectoria de la parábola debido a una fuerza inversa del cuadrado dirigida hacia S, el área SVB aumenta a una velocidad constante a medida que el punto B se mueve hacia adelante. De ello se deduce que J se mueve a velocidad constante a lo largo de VX a medida que B se mueve a lo largo de la parábola.
Si la velocidad del cuerpo en el vértice donde se mueve perpendicularmente a SV es v , entonces la velocidad de J es igual a 3 v /4 .
La construcción se puede extender simplemente para incluir el caso en el que ninguno de los radios coincide con el eje SV de la siguiente manera. Sea A un punto fijo en VG entre V y B, y el punto H la intersección en VX con la perpendicular a SA en A. De lo anterior, el área del sector parabólico .
Por el contrario, si se requiere encontrar el punto B para un área particular SAB, se encuentra el punto J desde HJ y el punto B como antes. Según el Libro 1, Proposición 16, Corolario 6 de los Principia de Newton , la velocidad de un cuerpo que se mueve a lo largo de una parábola con una fuerza dirigida hacia el foco es inversamente proporcional a la raíz cuadrada del radio. Si la velocidad en A es v , entonces en el vértice V es , y el punto J se mueve a una velocidad constante de .
La construcción anterior fue ideada por Isaac Newton y se puede encontrar en el Libro 1 de Philosophiæ Naturalis Principia Mathematica como Proposición 30.
La distancia focal de una parábola es la mitad de su radio de curvatura en su vértice.
Consideremos un punto ( x , y ) en un círculo de radio R y con centro en el punto (0, R ) . El círculo pasa por el origen. Si el punto está cerca del origen, el teorema de Pitágoras demuestra que
Pero si ( x , y ) está extremadamente cerca del origen, ya que el eje x es una tangente al círculo, y es muy pequeña comparada con x , por lo que y 2 es despreciable en comparación con los otros términos. Por lo tanto, extremadamente cerca del origen
Compare esto con la parábola
que tiene su vértice en el origen, se abre hacia arriba y tiene una distancia focal f (ver secciones anteriores de este artículo).
Las ecuaciones (1) y (2) son equivalentes si R = 2 f . Por lo tanto, esta es la condición para que el círculo y la parábola coincidan en el origen y extremadamente cerca de él. El radio de curvatura en el origen, que es el vértice de la parábola, es el doble de la distancia focal.
Un espejo cóncavo, que es un pequeño segmento de una esfera, se comporta aproximadamente como un espejo parabólico, enfocando la luz paralela en un punto intermedio entre el centro y la superficie de la esfera.
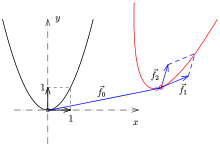
Otra definición de parábola utiliza transformaciones afines :
Una transformación afín del plano euclidiano tiene la forma , donde es una matriz regular ( el determinante no es 0) y es un vector arbitrario. Si son los vectores columna de la matriz , la parábola unitaria se mapea sobre la parábola donde
En general, los dos vectores no son perpendiculares, y no es el vértice, a menos que la transformación afín sea una semejanza .
El vector tangente en el punto es . En el vértice el vector tangente es ortogonal a . Por lo tanto el parámetro del vértice es la solución de la ecuación que es y el vértice es
La distancia focal se puede determinar mediante una transformación de parámetros adecuada (que no cambia la forma geométrica de la parábola). La distancia focal es Por lo tanto, el foco de la parábola es
Resolviendo la representación paramétrica para mediante la regla de Cramer y utilizando , se obtiene la representación implícita
La definición de parábola en esta sección da una representación paramétrica de una parábola arbitraria, incluso en el espacio, si se permiten vectores en el espacio.
Una curva de Bézier cuadrática es una curva definida por tres puntos , y , llamados sus puntos de control :
Esta curva es un arco de una parábola (ver § Como imagen afín de la parábola unitaria).
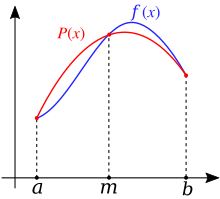
En un método de integración numérica se reemplaza la gráfica de una función por arcos de parábolas e integra los arcos de parábola. Una parábola se determina mediante tres puntos. La fórmula para un arco es
El método se llama regla de Simpson .
Las siguientes cuádricas contienen parábolas como secciones planas:
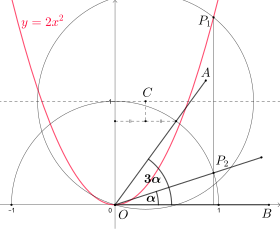
Una parábola puede utilizarse como trisectriz , es decir, permite la trisección exacta de un ángulo arbitrario con regla y compás. Esto no está en contradicción con la imposibilidad de una trisección de ángulos con construcciones con regla y compás únicamente, ya que el uso de parábolas no está permitido en las reglas clásicas para construcciones con regla y compás.
Para trisecar , coloque su cateto en el eje x de modo que el vértice esté en el origen del sistema de coordenadas. El sistema de coordenadas también contiene la parábola . El círculo unitario con radio 1 alrededor del origen interseca el otro cateto del ángulo , y desde este punto de intersección traza la perpendicular sobre el eje y. La paralela al eje y que pasa por el punto medio de esa perpendicular y la tangente en el círculo unitario en intersecan en . El círculo alrededor con radio interseca la parábola en . La perpendicular desde sobre el eje x interseca el círculo unitario en , y es exactamente un tercio de .
La exactitud de esta construcción se puede comprobar mostrando que la coordenada x de es . Resolviendo el sistema de ecuaciones dado por el círculo alrededor y la parábola se llega a la ecuación cúbica . La fórmula del triple ángulo muestra que es de hecho una solución de esa ecuación cúbica.
Esta trisección se remonta a René Descartes , quien la describió en su libro La Géométrie (1637). [18]
Si uno reemplaza los números reales por un campo arbitrario , muchas propiedades geométricas de la parábola siguen siendo válidas:
Surgen fenómenos esencialmente nuevos si el campo tiene la característica 2 (es decir, ): las tangentes son todas paralelas.
En geometría algebraica , la parábola se generaliza mediante las curvas normales racionales , que tienen coordenadas ( x , x 2 , x 3 , ..., x n ) ; la parábola estándar es el caso n = 2 , y el caso n = 3 se conoce como cúbica torcida . Una generalización adicional la da la variedad veronesa , cuando hay más de una variable de entrada.
En la teoría de formas cuadráticas , la parábola es el gráfico de la forma cuadrática x 2 (u otras escalas), mientras que el paraboloide elíptico es el gráfico de la forma cuadrática positiva definida x 2 + y 2 (o escalas), y el paraboloide hiperbólico es el gráfico de la forma cuadrática indefinida x 2 − y 2 . Las generalizaciones a más variables producen más objetos de este tipo.
Las curvas y = x p para otros valores de p se denominan tradicionalmente parábolas superiores y se trataron originalmente de forma implícita, en la forma x p = ky q para p y q ambos enteros positivos, en cuya forma se las considera curvas algebraicas. Estas corresponden a la fórmula explícita y = x p / q para una potencia fraccionaria positiva de x . Las potencias fraccionarias negativas corresponden a la ecuación implícita x p y q = k y se denominan tradicionalmente hipérbolas superiores . Analíticamente, x también se puede elevar a una potencia irracional (para valores positivos de x ); las propiedades analíticas son análogas a cuando x se eleva a potencias racionales, pero la curva resultante ya no es algebraica y no se puede analizar mediante geometría algebraica.
En la naturaleza, las aproximaciones de parábolas y paraboloides se encuentran en muchas situaciones diversas. El ejemplo más conocido de parábola en la historia de la física es la trayectoria de una partícula o cuerpo en movimiento bajo la influencia de un campo gravitatorio uniforme sin resistencia del aire (por ejemplo, una pelota volando por el aire, sin tener en cuenta la fricción del aire ).
La trayectoria parabólica de los proyectiles fue descubierta experimentalmente a principios del siglo XVII por Galileo , quien realizó experimentos con bolas rodando sobre planos inclinados. Posteriormente también lo demostró matemáticamente en su libro Diálogo sobre dos nuevas ciencias . [19] [h] Para los objetos extendidos en el espacio, como un saltador que salta de un trampolín, el objeto en sí sigue un movimiento complejo a medida que gira, pero el centro de masa del objeto se mueve, no obstante, a lo largo de una parábola. Como en todos los casos en el mundo físico, la trayectoria es siempre una aproximación de una parábola. La presencia de resistencia del aire, por ejemplo, siempre distorsiona la forma, aunque a bajas velocidades, la forma es una buena aproximación de una parábola. A velocidades más altas, como en balística, la forma está muy distorsionada y no se parece a una parábola.
Otra situación hipotética en la que podrían surgir parábolas, según las teorías de la física descritas en los siglos XVII y XVIII por Sir Isaac Newton , es en órbitas de dos cuerpos , por ejemplo, la trayectoria de un pequeño planetoide u otro objeto bajo la influencia de la gravitación del Sol . Las órbitas parabólicas no ocurren en la naturaleza; las órbitas simples se parecen más comúnmente a hipérbolas o elipses . La órbita parabólica es el caso intermedio degenerado entre esos dos tipos de órbita ideal. Un objeto que sigue una órbita parabólica viajaría a la velocidad de escape exacta del objeto que orbita; los objetos en órbitas elípticas o hiperbólicas viajan a menor o mayor que la velocidad de escape, respectivamente. Los cometas de período largo viajan cerca de la velocidad de escape del Sol mientras se mueven a través del sistema solar interior, por lo que sus trayectorias son casi parabólicas.
También se encuentran aproximaciones de parábolas en la forma de los cables principales de un puente colgante simple . La curva de las cadenas de un puente colgante es siempre una curva intermedia entre una parábola y una catenaria , pero en la práctica la curva generalmente está más cerca de una parábola debido a que el peso de la carga (es decir, la carretera) es mucho mayor que los propios cables, y en los cálculos se utiliza la fórmula polinómica de segundo grado de una parábola. [20] [21] Bajo la influencia de una carga uniforme (como una plataforma suspendida horizontal), el cable, que de otro modo tendría forma de catenaria, se deforma hacia una parábola (véase Catenaria § Curva del puente colgante ). A diferencia de una cadena inelástica, un resorte que cuelga libremente de longitud no estresada cero toma la forma de una parábola. Los cables de los puentes colgantes están, idealmente, puramente en tensión, sin tener que soportar otras fuerzas, por ejemplo, la flexión. De manera similar, las estructuras de los arcos parabólicos están puramente en compresión.
Los paraboloides también surgen en varias situaciones físicas. El ejemplo más conocido es el reflector parabólico , que es un espejo o dispositivo reflector similar que concentra la luz u otras formas de radiación electromagnética en un punto focal común o, por el contrario, colima la luz desde una fuente puntual en el foco en un haz paralelo. El principio del reflector parabólico puede haber sido descubierto en el siglo III a. C. por el geómetra Arquímedes , quien, según una dudosa leyenda, [22] construyó espejos parabólicos para defender Siracusa contra la flota romana , concentrando los rayos del sol para prender fuego a las cubiertas de los barcos romanos. El principio se aplicó a los telescopios en el siglo XVII. Hoy en día, los reflectores paraboloides se pueden observar comúnmente en gran parte del mundo en antenas receptoras y transmisoras de microondas y antenas parabólicas.
En los micrófonos parabólicos , se utiliza un reflector parabólico para enfocar el sonido hacia un micrófono, lo que le otorga un rendimiento altamente direccional.
Los paraboloides también se observan en la superficie de un líquido confinado en un recipiente y girado alrededor de su eje central. En este caso, la fuerza centrífuga hace que el líquido suba por las paredes del recipiente, formando una superficie parabólica. Este es el principio en el que se basa el telescopio de espejo líquido .
Las aeronaves utilizadas para crear un estado de ingravidez con fines experimentales, como el " Vomit Comet " de la NASA , siguen una trayectoria parabólica vertical durante breves períodos para trazar el curso de un objeto en caída libre , lo que produce el mismo efecto que la gravedad cero para la mayoría de los propósitos.