La teoría M es una teoría de la física que unifica todas las versiones consistentes de la teoría de supercuerdas . Edward Witten fue el primero en conjeturar la existencia de dicha teoría en una conferencia sobre teoría de cuerdas en la Universidad del Sur de California en 1995. El anuncio de Witten inició una oleada de actividad de investigación conocida como la segunda revolución de las supercuerdas . Antes del anuncio de Witten, los teóricos de cuerdas habían identificado cinco versiones de la teoría de supercuerdas. Aunque estas teorías inicialmente parecían ser muy diferentes, el trabajo de muchos físicos mostró que las teorías estaban relacionadas de maneras intrincadas y no triviales. Los físicos descubrieron que teorías aparentemente distintas podían unificarse mediante transformaciones matemáticas llamadas dualidad S y dualidad T. La conjetura de Witten se basó en parte en la existencia de estas dualidades y en parte en la relación de las teorías de cuerdas con una teoría de campo llamada supergravedad de once dimensiones .
Aunque no se conoce una formulación completa de la teoría M, dicha formulación debería describir objetos bidimensionales y pentadimensionales llamados branas y debería ser aproximada por la supergravedad de once dimensiones a bajas energías . Los intentos modernos de formular la teoría M se basan típicamente en la teoría de matrices o la correspondencia AdS/CFT . Según Witten, M debería significar "magia", "misterio" o "membrana" según el gusto, y el verdadero significado del título debería decidirse cuando se conozca una formulación más fundamental de la teoría. [1]
Las investigaciones sobre la estructura matemática de la teoría M han dado lugar a importantes resultados teóricos en física y matemáticas. En términos más especulativos, la teoría M puede proporcionar un marco para desarrollar una teoría unificada de todas las fuerzas fundamentales de la naturaleza. Los intentos de conectar la teoría M con la experimentación suelen centrarse en compactar sus dimensiones adicionales para construir modelos candidatos del mundo de cuatro dimensiones, aunque hasta ahora no se ha verificado que ninguno dé lugar a la física observada en los experimentos de física de alta energía .

Uno de los problemas más profundos de la física moderna es el de la gravedad cuántica . La comprensión actual de la gravedad se basa en la teoría general de la relatividad de Albert Einstein , que está formulada en el marco de la física clásica . Sin embargo, las fuerzas no gravitacionales se describen en el marco de la mecánica cuántica , un formalismo radicalmente diferente para describir fenómenos físicos basados en la probabilidad . [a] Se necesita una teoría cuántica de la gravedad para reconciliar la relatividad general con los principios de la mecánica cuántica, [b] pero surgen dificultades cuando se intenta aplicar las prescripciones habituales de la teoría cuántica a la fuerza de la gravedad. [c]
La teoría de cuerdas es un marco teórico que intenta reconciliar la gravedad y la mecánica cuántica. En la teoría de cuerdas, las partículas puntuales de la física de partículas son reemplazadas por objetos unidimensionales llamados cuerdas . La teoría de cuerdas describe cómo las cuerdas se propagan a través del espacio e interactúan entre sí. En una versión dada de la teoría de cuerdas, solo hay un tipo de cuerda, que puede parecer un pequeño bucle o segmento de cuerda ordinaria, y puede vibrar de diferentes maneras. En escalas de distancia mayores que la escala de cuerdas, una cuerda se verá como una partícula ordinaria, con su masa , carga y otras propiedades determinadas por el estado vibracional de la cuerda. De esta manera, todas las diferentes partículas elementales pueden verse como cuerdas vibrantes. Uno de los estados vibracionales de una cuerda da lugar al gravitón , una partícula mecánica cuántica que transporta fuerza gravitatoria. [d]
Existen varias versiones de la teoría de cuerdas: tipo I , tipo IIA , tipo IIB y dos variantes de la teoría de cuerdas heterótica ( SO (32) y E 8 × E 8 ). Las diferentes teorías permiten diferentes tipos de cuerdas, y las partículas que surgen a bajas energías exhiben diferentes simetrías . Por ejemplo, la teoría de tipo I incluye tanto cuerdas abiertas (que son segmentos con puntos finales) como cuerdas cerradas (que forman bucles cerrados), mientras que los tipos IIA y IIB incluyen solo cuerdas cerradas. [2] Cada una de estas cinco teorías de cuerdas surge como un caso límite especial de la teoría M. Esta teoría, al igual que sus predecesoras de la teoría de cuerdas, es un ejemplo de una teoría cuántica de la gravedad. Describe una fuerza como la familiar fuerza gravitacional sujeta a las reglas de la mecánica cuántica. [3]

En la vida cotidiana, existen tres dimensiones familiares del espacio: altura, anchura y profundidad. La teoría general de la relatividad de Einstein trata el tiempo como una dimensión a la par de las tres dimensiones espaciales; en la relatividad general, el espacio y el tiempo no se modelan como entidades separadas, sino que se unifican en un espacio-tiempo de cuatro dimensiones , tres dimensiones espaciales y una dimensión temporal. En este marco, el fenómeno de la gravedad se considera una consecuencia de la geometría del espacio-tiempo. [4]
A pesar de que el universo está bien descrito por el espacio-tiempo de cuatro dimensiones, hay varias razones por las que los físicos consideran teorías en otras dimensiones. En algunos casos, al modelar el espacio-tiempo en un número diferente de dimensiones, una teoría se vuelve más manejable matemáticamente y uno puede realizar cálculos y obtener conocimientos generales con mayor facilidad. [e] También hay situaciones en las que las teorías en dos o tres dimensiones del espacio-tiempo son útiles para describir fenómenos en la física de la materia condensada . [5] Finalmente, existen escenarios en los que en realidad podría haber más de cuatro dimensiones del espacio-tiempo que, no obstante, han logrado escapar a la detección. [6]
Una característica notable de la teoría de cuerdas y la teoría M es que estas teorías requieren dimensiones adicionales del espacio-tiempo para su consistencia matemática. En la teoría de cuerdas, el espacio-tiempo tiene diez dimensiones (nueve dimensiones espaciales y una dimensión temporal).Mientras que en la teoría M es de once dimensiones (diez dimensiones espaciales y una dimensión temporal). Para describir fenómenos físicos reales utilizando estas teorías, uno debe imaginar escenarios en los que estas dimensiones adicionales no se observarían en los experimentos. [7]
La compactificación es una forma de modificar el número de dimensiones en una teoría física. [f] En la compactificación, se supone que algunas de las dimensiones adicionales se "cierran" sobre sí mismas para formar círculos. [8] En el límite en el que estas dimensiones enrolladas se vuelven muy pequeñas, se obtiene una teoría en la que el espacio-tiempo tiene efectivamente un número menor de dimensiones. Una analogía estándar para esto es considerar un objeto multidimensional como una manguera de jardín. Si la manguera se ve desde una distancia suficiente, parece tener solo una dimensión, su longitud. Sin embargo, al acercarse a la manguera, se descubre que contiene una segunda dimensión, su circunferencia. Por lo tanto, una hormiga que se arrastrara sobre la superficie de la manguera se movería en dos dimensiones. [g]
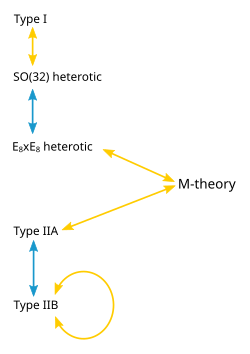
Las teorías que surgen como diferentes límites de la teoría M resultan estar relacionadas de maneras altamente no triviales. Una de las relaciones que pueden existir entre estas diferentes teorías físicas se llama S-dualidad . Esta es una relación que dice que una colección de partículas que interactúan fuertemente en una teoría puede, en algunos casos, ser vista como una colección de partículas que interactúan débilmente en una teoría completamente diferente. En términos generales, se dice que una colección de partículas interactúa fuertemente si se combinan y decaen a menudo y que interactúan débilmente si lo hacen con poca frecuencia. La teoría de cuerdas de tipo I resulta ser equivalente por S-dualidad a la teoría de cuerdas heterótica SO (32) . De manera similar, la teoría de cuerdas de tipo IIB está relacionada consigo misma de una manera no trivial por S-dualidad. [10]
Otra relación entre diferentes teorías de cuerdas es la T-dualidad . Aquí se consideran cuerdas que se propagan alrededor de una dimensión extra circular. La T-dualidad establece que una cuerda que se propaga alrededor de un círculo de radio R es equivalente a una cuerda que se propaga alrededor de un círculo de radio 1/ R en el sentido de que todas las cantidades observables en una descripción se identifican con cantidades en la descripción dual. Por ejemplo, una cuerda tiene momento mientras se propaga alrededor de un círculo, y también puede enrollarse alrededor del círculo una o más veces. El número de veces que la cuerda se enrolla alrededor de un círculo se llama número de enrollamiento . Si una cuerda tiene momento p y número de enrollamiento n en una descripción, tendrá momento n y número de enrollamiento p en la descripción dual. Por ejemplo, la teoría de cuerdas de tipo IIA es equivalente a la teoría de cuerdas de tipo IIB a través de la T-dualidad, y las dos versiones de la teoría de cuerdas heterótica también están relacionadas por la T-dualidad. [10]
En general, el término dualidad se refiere a una situación en la que dos sistemas físicos aparentemente diferentes resultan ser equivalentes de una manera no trivial. Si dos teorías están relacionadas por una dualidad, significa que una teoría puede transformarse de alguna manera para que termine pareciendo exactamente igual a la otra teoría. Se dice entonces que las dos teorías son duales entre sí bajo la transformación. Dicho de otra manera, las dos teorías son descripciones matemáticamente diferentes de los mismos fenómenos. [11]
Otra idea teórica importante que juega un papel en la teoría M es la supersimetría . Se trata de una relación matemática que existe en ciertas teorías físicas entre una clase de partículas llamadas bosones y una clase de partículas llamadas fermiones . En términos generales, los fermiones son los constituyentes de la materia, mientras que los bosones median las interacciones entre partículas. En las teorías con supersimetría, cada bosón tiene una contraparte que es un fermión, y viceversa. Cuando la supersimetría se impone como una simetría local, se obtiene automáticamente una teoría mecánica cuántica que incluye la gravedad. Tal teoría se llama teoría de supergravedad . [12]
Una teoría de cuerdas que incorpora la idea de supersimetría se denomina teoría de supercuerdas . Existen varias versiones diferentes de la teoría de supercuerdas, todas ellas incluidas en el marco de la teoría M. A bajas energías , las teorías de supercuerdas se aproximan mediante una de las tres supergravedades en diez dimensiones, conocidas como supergravedad de tipo I , tipo IIA y tipo IIB . De manera similar, la teoría M se aproxima a bajas energías mediante la supergravedad en once dimensiones. [3]
En la teoría de cuerdas y teorías relacionadas, como las teorías de supergravedad, una brana es un objeto físico que generaliza la noción de una partícula puntual a dimensiones superiores. Por ejemplo, una partícula puntual puede considerarse una brana de dimensión cero, mientras que una cuerda puede considerarse una brana de dimensión uno. También es posible considerar branas de dimensiones superiores. En la dimensión p , se denominan p -branas. Las branas son objetos dinámicos que pueden propagarse a través del espacio-tiempo según las reglas de la mecánica cuántica. Pueden tener masa y otros atributos como carga. Una p -brana barre un volumen ( p + 1) -dimensional en el espacio-tiempo llamado su volumen mundial . Los físicos a menudo estudian campos análogos al campo electromagnético que viven en el volumen mundial de una brana. La palabra brana proviene de la palabra "membrana" que se refiere a una brana bidimensional. [13]
En la teoría de cuerdas, los objetos fundamentales que dan origen a las partículas elementales son las cuerdas unidimensionales. Aunque los fenómenos físicos descritos por la teoría M aún no se comprenden bien, los físicos saben que la teoría describe branas bidimensionales y pentadimensionales. Gran parte de la investigación actual en la teoría M intenta comprender mejor las propiedades de estas branas. [h]
A principios del siglo XX, físicos y matemáticos como Albert Einstein y Hermann Minkowski fueron pioneros en el uso de la geometría cuatridimensional para describir el mundo físico. [14] Estos esfuerzos culminaron en la formulación de la teoría general de la relatividad de Einstein, que relaciona la gravedad con la geometría del espacio-tiempo cuatridimensional. [15]
El éxito de la relatividad general condujo a esfuerzos por aplicar la geometría de dimensiones superiores para explicar otras fuerzas. En 1919, el trabajo de Theodor Kaluza demostró que al pasar al espacio-tiempo de cinco dimensiones, se pueden unificar la gravedad y el electromagnetismo en una sola fuerza. [15] Esta idea fue mejorada por el físico Oskar Klein , quien sugirió que la dimensión adicional propuesta por Kaluza podría tomar la forma de un círculo con un radio de alrededor de 10 −30 cm. [16]
La teoría de Kaluza-Klein y los intentos posteriores de Einstein de desarrollar la teoría del campo unificado nunca tuvieron un éxito total. En parte, esto se debió a que la teoría de Kaluza-Klein predijo una partícula (el radión ), cuya existencia nunca se ha demostrado, y en parte a que no pudo predecir correctamente la relación entre la masa de un electrón y su carga. Además, estas teorías se estaban desarrollando justo cuando otros físicos comenzaban a descubrir la mecánica cuántica, que finalmente demostraría ser exitosa en la descripción de fuerzas conocidas como el electromagnetismo, así como nuevas fuerzas nucleares que se estaban descubriendo a lo largo de la mitad del siglo. Por lo tanto, se necesitarían casi cincuenta años para que la idea de nuevas dimensiones volviera a tomarse en serio. [17]

Nuevos conceptos y herramientas matemáticas proporcionaron nuevas perspectivas sobre la relatividad general, dando lugar a un período en la década de 1960 y 1970 ahora conocido como la edad de oro de la relatividad general . [18] A mediados de la década de 1970, los físicos comenzaron a estudiar teorías de dimensiones superiores que combinaban la relatividad general con la supersimetría, las llamadas teorías de supergravedad. [19]
La relatividad general no impone ningún límite a las posibles dimensiones del espacio-tiempo. Aunque la teoría se formula típicamente en cuatro dimensiones, se pueden escribir las mismas ecuaciones para el campo gravitatorio en cualquier número de dimensiones. La supergravedad es más restrictiva porque impone un límite superior al número de dimensiones. [12] En 1978, el trabajo de Werner Nahm demostró que la dimensión máxima del espacio-tiempo en la que se puede formular una teoría supersimétrica consistente es once. [20] En el mismo año, Eugène Cremmer , Bernard Julia y Joël Scherk de la École Normale Supérieure demostraron que la supergravedad no solo permite hasta once dimensiones, sino que de hecho es más elegante en este número máximo de dimensiones. [21] [22]
Inicialmente, muchos físicos esperaban que, compactando la supergravedad de once dimensiones, sería posible construir modelos realistas de nuestro mundo de cuatro dimensiones. La esperanza era que dichos modelos proporcionarían una descripción unificada de las cuatro fuerzas fundamentales de la naturaleza: el electromagnetismo, las fuerzas nucleares fuerte y débil y la gravedad. El interés en la supergravedad de once dimensiones pronto disminuyó a medida que se descubrieron varios fallos en este esquema. Uno de los problemas era que las leyes de la física parecen distinguir entre el sentido de las agujas del reloj y el sentido contrario a las agujas del reloj, un fenómeno conocido como quiralidad . Edward Witten y otros observaron que esta propiedad de quiralidad no se puede derivar fácilmente compactando a partir de once dimensiones. [22]
En la primera revolución de las supercuerdas en 1984, muchos físicos recurrieron a la teoría de cuerdas como una teoría unificada de la física de partículas y la gravedad cuántica. A diferencia de la teoría de la supergravedad, la teoría de cuerdas fue capaz de adaptarse a la quiralidad del modelo estándar y proporcionó una teoría de la gravedad coherente con los efectos cuánticos. [22] Otra característica de la teoría de cuerdas que atrajo a muchos físicos en las décadas de 1980 y 1990 fue su alto grado de singularidad. En las teorías de partículas ordinarias, se puede considerar cualquier conjunto de partículas elementales cuyo comportamiento clásico se describe mediante un lagrangiano arbitrario . En la teoría de cuerdas, las posibilidades están mucho más limitadas: en la década de 1990, los físicos habían argumentado que solo había cinco versiones supersimétricas consistentes de la teoría. [22]
Aunque sólo había un puñado de teorías de supercuerdas consistentes, seguía siendo un misterio por qué no había una única formulación consistente. [22] Sin embargo, cuando los físicos comenzaron a examinar la teoría de cuerdas más de cerca, se dieron cuenta de que estas teorías están relacionadas de maneras intrincadas y no triviales. [23]
A finales de los años 1970, Claus Montonen y David Olive habían conjeturado una propiedad especial de ciertas teorías físicas. [24] Una versión afinada de su conjetura se refiere a una teoría llamada teoría supersimétrica de Yang-Mills N = 4 , que describe partículas teóricas formalmente similares a los quarks y gluones que forman los núcleos atómicos . La fuerza con la que interactúan las partículas de esta teoría se mide por un número llamado constante de acoplamiento . El resultado de Montonen y Olive, ahora conocido como dualidad Montonen-Olive , establece que la teoría supersimétrica de Yang-Mills N = 4 con constante de acoplamiento g es equivalente a la misma teoría con constante de acoplamiento 1/ g . En otras palabras, un sistema de partículas que interactúan fuertemente (constante de acoplamiento grande) tiene una descripción equivalente como un sistema de partículas que interactúan débilmente (constante de acoplamiento pequeña) y viceversa [25] por el momento de espín.
En la década de 1990, varios teóricos generalizaron la dualidad Montonen-Olive a la relación de dualidad S, que conecta diferentes teorías de cuerdas. Ashoke Sen estudió la dualidad S en el contexto de cuerdas heteróticas en cuatro dimensiones. [26] [27] Chris Hull y Paul Townsend demostraron que la teoría de cuerdas de tipo IIB con una gran constante de acoplamiento es equivalente a través de la dualidad S a la misma teoría con una pequeña constante de acoplamiento. [28] Los teóricos también descubrieron que diferentes teorías de cuerdas pueden estar relacionadas por la dualidad T. Esta dualidad implica que las cuerdas que se propagan en geometrías de espacio-tiempo completamente diferentes pueden ser físicamente equivalentes. [29]
La teoría de cuerdas amplía la física de partículas ordinarias al reemplazar partículas puntuales de dimensión cero por objetos unidimensionales llamados cuerdas. A fines de la década de 1980, era natural que los teóricos intentaran formular otras extensiones en las que las partículas fueran reemplazadas por supermembranas bidimensionales o por objetos de dimensiones superiores llamados branas. Tales objetos habían sido considerados ya en 1962 por Paul Dirac [ 30] y fueron reconsiderados por un pequeño pero entusiasta grupo de físicos en la década de 1980 [22] .
La supersimetría restringe severamente el número posible de dimensiones de una brana. En 1987, Eric Bergshoeff, Ergin Sezgin y Paul Townsend demostraron que la supergravedad de once dimensiones incluye branas bidimensionales. [31] Intuitivamente, estos objetos parecen láminas o membranas que se propagan a través del espacio-tiempo de once dimensiones. Poco después de este descubrimiento, Michael Duff , Paul Howe, Takeo Inami y Kellogg Stelle consideraron una compactificación particular de la supergravedad de once dimensiones con una de las dimensiones enrollada en un círculo. [32] En este contexto, uno puede imaginar la membrana envolviendo la dimensión circular. Si el radio del círculo es suficientemente pequeño, entonces esta membrana se ve como una cuerda en el espacio-tiempo de diez dimensiones. De hecho, Duff y sus colaboradores demostraron que esta construcción reproduce exactamente las cuerdas que aparecen en la teoría de supercuerdas de tipo IIA. [25]
En 1990, Andrew Strominger publicó un resultado similar que sugería que las cuerdas que interactúan fuertemente en diez dimensiones podrían tener una descripción equivalente en términos de branas pentadimensionales que interactúan débilmente. [33] Inicialmente, los físicos no pudieron demostrar esta relación por dos razones importantes. Por un lado, la dualidad Montonen-Olive aún no estaba probada, y por lo tanto la conjetura de Strominger era aún más tenue. Por otro lado, había muchos problemas técnicos relacionados con las propiedades cuánticas de las branas pentadimensionales. [34] El primero de estos problemas se resolvió en 1993 cuando Ashoke Sen estableció que ciertas teorías físicas requieren la existencia de objetos con carga eléctrica y magnética que fueron predichas por el trabajo de Montonen y Olive. [35]
A pesar de estos avances, la relación entre cuerdas y branas pentadimensionales siguió siendo conjetural, porque los teóricos no eran capaces de cuantificar las branas. A partir de 1991, un equipo de investigadores, entre los que se encontraban Michael Duff, Ramzi Khuri, Jianxin Lu y Ruben Minasian, consideró una compactificación especial de la teoría de cuerdas en la que cuatro de las diez dimensiones se enroscan. Si se considera una brana pentadimensional envuelta alrededor de estas dimensiones adicionales, entonces la brana parece una cuerda unidimensional. De esta manera, la relación conjeturada entre cuerdas y branas se redujo a una relación entre cuerdas y cuerdas, y esta última se pudo comprobar utilizando técnicas teóricas ya establecidas. [29]

En 1995, en una conferencia sobre teoría de cuerdas en la Universidad del Sur de California , Edward Witten, del Instituto de Estudios Avanzados, hizo la sorprendente sugerencia de que las cinco teorías de supercuerdas eran, de hecho, sólo casos límite diferentes de una única teoría en once dimensiones del espacio-tiempo. El anuncio de Witten reunía todos los resultados anteriores sobre la dualidad S y T y la aparición de branas bidimensionales y pentadimensionales en la teoría de cuerdas. [36] En los meses posteriores al anuncio de Witten, aparecieron cientos de nuevos artículos en Internet que confirmaban que la nueva teoría involucraba a las membranas de una manera importante. [37] Hoy en día, esta oleada de trabajos se conoce como la segunda revolución de las supercuerdas . [38]
Uno de los desarrollos importantes posteriores al anuncio de Witten fue el trabajo que realizó en 1996 con el teórico de cuerdas Petr Hořava . [39] [40] Witten y Hořava estudiaron la teoría M en una geometría especial del espacio-tiempo con dos componentes de contorno decadimensionales. Su trabajo arrojó luz sobre la estructura matemática de la teoría M y sugirió posibles formas de conectar la teoría M con la física del mundo real. [41]
Inicialmente, algunos físicos sugirieron que la nueva teoría era una teoría fundamental de las membranas, pero Witten se mostró escéptico respecto del papel de las membranas en la teoría. En un artículo de 1996, Hořava y Witten escribieron:
Como se ha propuesto que la teoría de once dimensiones es una teoría de supermembranas, pero hay algunas razones para dudar de esa interpretación, la llamaremos sin compromiso la teoría M, dejando para el futuro la relación de M con las membranas. [39]
En ausencia de una comprensión del verdadero significado y la estructura de la teoría M, Witten ha sugerido que la M debería significar "magia", "misterio" o "membrana", según el gusto, y que el verdadero significado del título debería decidirse cuando se conozca una formulación más fundamental de la teoría. [1] Años más tarde, afirmaría: "Pensé que mis colegas entenderían que realmente significaba membrana. Desafortunadamente, la gente se confundió". [42]
En matemáticas, una matriz es una disposición rectangular de números u otros datos. En física, un modelo matricial es un tipo particular de teoría física cuya formulación matemática involucra la noción de matriz de manera importante. Un modelo matricial describe el comportamiento de un conjunto de matrices dentro del marco de la mecánica cuántica. [43] [44]
Un ejemplo importante [¿ por qué? ] de un modelo matricial es el modelo matricial BFSS propuesto por Tom Banks , Willy Fischler , Stephen Shenker y Leonard Susskind en 1997. Esta teoría describe el comportamiento de un conjunto de nueve matrices grandes. En su artículo original, estos autores demostraron, entre otras cosas, que el límite de baja energía de este modelo matricial se describe mediante la supergravedad de once dimensiones. Estos cálculos los llevaron a proponer que el modelo matricial BFSS es exactamente equivalente a la teoría M. Por lo tanto, el modelo matricial BFSS puede usarse como prototipo para una formulación correcta de la teoría M y como herramienta para investigar las propiedades de la teoría M en un entorno relativamente simple. [43] [ aclaración necesaria ]
En geometría, a menudo resulta útil introducir las coordenadas . Por ejemplo, para estudiar la geometría del plano euclidiano , se definen las coordenadas x e y como las distancias entre cualquier punto del plano y un par de ejes . En la geometría ordinaria, las coordenadas de un punto son números, por lo que se pueden multiplicar, y el producto de dos coordenadas no depende del orden de multiplicación. Es decir, xy = yx . Esta propiedad de la multiplicación se conoce como ley conmutativa , y esta relación entre la geometría y el álgebra conmutativa de coordenadas es el punto de partida de gran parte de la geometría moderna. [45]
La geometría no conmutativa es una rama de las matemáticas que intenta generalizar esta situación. En lugar de trabajar con números ordinarios, se consideran algunos objetos similares, como matrices, cuya multiplicación no satisface la ley conmutativa (es decir, objetos para los que xy no es necesariamente igual a yx ). Se imagina que estos objetos no conmutativos son coordenadas de alguna noción más general de "espacio" y se prueban teoremas sobre estos espacios generalizados explotando la analogía con la geometría ordinaria. [46]
En un artículo de 1998, Alain Connes , Michael R. Douglas y Albert Schwarz demostraron que algunos aspectos de los modelos matriciales y la teoría M se describen mediante una teoría cuántica de campos no conmutativa , un tipo especial de teoría física en la que las coordenadas en el espacio-tiempo no satisfacen la propiedad de conmutatividad. [44] Esto estableció un vínculo entre los modelos matriciales y la teoría M por un lado, y la geometría no conmutativa por el otro. Rápidamente condujo al descubrimiento de otros vínculos importantes entre la geometría no conmutativa y varias teorías físicas. [47] [48]

La aplicación de la mecánica cuántica a objetos físicos como el campo electromagnético, que se extienden en el espacio y el tiempo, se conoce como teoría cuántica de campos . [i] En física de partículas, las teorías cuánticas de campos forman la base para nuestra comprensión de las partículas elementales, que se modelan como excitaciones en los campos fundamentales. Las teorías cuánticas de campos también se utilizan en toda la física de la materia condensada para modelar objetos similares a partículas llamados cuasipartículas . [j]
Un enfoque para formular la teoría M y estudiar sus propiedades lo proporciona la correspondencia anti-de Sitter/teoría conforme de campos (AdS/CFT) . Propuesta por Juan Maldacena a finales de 1997, la correspondencia AdS/CFT es un resultado teórico que implica que la teoría M es en algunos casos equivalente a una teoría cuántica de campos. [49] Además de proporcionar información sobre la estructura matemática de la teoría de cuerdas y la teoría M, la correspondencia AdS/CFT ha arrojado luz sobre muchos aspectos de la teoría cuántica de campos en regímenes donde las técnicas de cálculo tradicionales son ineficaces. [50]
En la correspondencia AdS/CFT, la geometría del espacio-tiempo se describe en términos de una determinada solución de vacío de la ecuación de Einstein llamada espacio anti-de Sitter . [51] En términos muy elementales, el espacio anti-de Sitter es un modelo matemático del espacio-tiempo en el que la noción de distancia entre puntos (la métrica ) es diferente de la noción de distancia en la geometría euclidiana ordinaria . Está estrechamente relacionado con el espacio hiperbólico , que puede verse como un disco como se ilustra a la izquierda. [52] Esta imagen muestra una teselación de un disco por triángulos y cuadrados. Se puede definir la distancia entre los puntos de este disco de tal manera que todos los triángulos y cuadrados tengan el mismo tamaño y el límite exterior circular esté infinitamente lejos de cualquier punto en el interior. [53]

Ahora imaginemos una pila de discos hiperbólicos donde cada uno de ellos representa el estado del universo en un momento dado. El objeto geométrico resultante es un espacio anti-de Sitter tridimensional. [52] Parece un cilindro sólido en el que cualquier sección transversal es una copia del disco hiperbólico. El tiempo transcurre a lo largo de la dirección vertical en esta imagen. La superficie de este cilindro desempeña un papel importante en la correspondencia AdS/CFT. Al igual que con el plano hiperbólico, el espacio anti-de Sitter está curvado de tal manera que cualquier punto en el interior está en realidad infinitamente lejos de esta superficie límite. [53]
Esta construcción describe un universo hipotético con sólo dos dimensiones espaciales y una temporal, pero puede generalizarse a cualquier número de dimensiones. De hecho, el espacio hiperbólico puede tener más de dos dimensiones y se pueden "apilar" copias del espacio hiperbólico para obtener modelos de dimensiones superiores del espacio anti-de Sitter. [52]
Una característica importante del espacio anti-de Sitter es su límite (que parece un cilindro en el caso del espacio anti-de Sitter tridimensional). Una propiedad de este límite es que, dentro de una pequeña región en la superficie alrededor de cualquier punto dado, se parece al espacio de Minkowski , el modelo de espacio-tiempo utilizado en la física no gravitacional. [54] Por lo tanto, se puede considerar una teoría auxiliar en la que el "espacio-tiempo" está dado por el límite del espacio anti-de Sitter. Esta observación es el punto de partida para la correspondencia AdS/CFT, que establece que el límite del espacio anti-de Sitter puede considerarse como el "espacio-tiempo" para una teoría cuántica de campos. La afirmación es que esta teoría cuántica de campos es equivalente a la teoría gravitacional en el espacio anti-de Sitter en masa en el sentido de que hay un "diccionario" para traducir entidades y cálculos en una teoría a sus contrapartes en la otra teoría. Por ejemplo, una sola partícula en la teoría gravitacional podría corresponder a alguna colección de partículas en la teoría del límite. Además, las predicciones en las dos teorías son cuantitativamente idénticas, de modo que si dos partículas tienen un 40 por ciento de posibilidades de colisionar en la teoría gravitacional, entonces las colecciones correspondientes en la teoría de límites también tendrían un 40 por ciento de posibilidades de colisionar. [55]

Una realización particular de la correspondencia AdS/CFT establece que la teoría M en el espacio de producto AdS 7 × S 4 es equivalente a la llamada teoría (2,0) en el límite de seis dimensiones. [49] Aquí "(2,0)" se refiere al tipo particular de supersimetría que aparece en la teoría. En este ejemplo, el espacio-tiempo de la teoría gravitacional es efectivamente heptadimensional (de ahí la notación AdS 7 ), y hay cuatro dimensiones " compactas " adicionales (codificadas por el factor S 4 ). En el mundo real, el espacio-tiempo es tetradimensional, al menos macroscópicamente, por lo que esta versión de la correspondencia no proporciona un modelo realista de la gravedad. Asimismo, la teoría dual no es un modelo viable de ningún sistema del mundo real, ya que describe un mundo con seis dimensiones espacio-temporales. [k]
Sin embargo, la teoría (2,0) ha demostrado ser importante para estudiar las propiedades generales de las teorías cuánticas de campos. De hecho, esta teoría subsume muchas teorías cuánticas de campos efectivas y matemáticamente interesantes y apunta a nuevas dualidades que relacionan estas teorías. Por ejemplo, Luis Alday, Davide Gaiotto y Yuji Tachikawa demostraron que al compactar esta teoría en una superficie , se obtiene una teoría cuántica de campos de cuatro dimensiones, y existe una dualidad conocida como la correspondencia AGT que relaciona la física de esta teoría con ciertos conceptos físicos asociados con la superficie misma. [56] Más recientemente, los teóricos han extendido estas ideas para estudiar las teorías obtenidas al compactar hasta tres dimensiones. [57]
Además de sus aplicaciones en la teoría cuántica de campos, la teoría (2,0) ha generado resultados importantes en matemáticas puras . Por ejemplo, la existencia de la teoría (2,0) fue utilizada por Witten para dar una explicación "física" para una relación conjetural en matemáticas llamada la correspondencia geométrica de Langlands . [58] En un trabajo posterior, Witten demostró que la teoría (2,0) podría usarse para comprender un concepto en matemáticas llamado homología de Khovanov . [59] Desarrollada por Mikhail Khovanov alrededor de 2000, la homología de Khovanov proporciona una herramienta en la teoría de nudos , la rama de las matemáticas que estudia y clasifica las diferentes formas de los nudos. [60] Otra aplicación de la teoría (2,0) en matemáticas es el trabajo de Davide Gaiotto , Greg Moore y Andrew Neitzke , que utilizaron ideas físicas para derivar nuevos resultados en la geometría de Hyperkähler . [61]
Otra realización de la correspondencia AdS/CFT establece que la teoría M sobre AdS 4 × S 7 es equivalente a una teoría cuántica de campos llamada teoría ABJM en tres dimensiones. En esta versión de la correspondencia, siete de las dimensiones de la teoría M están enrolladas, dejando cuatro dimensiones no compactas. Dado que el espacio-tiempo de nuestro universo es cuatridimensional, esta versión de la correspondencia proporciona una descripción algo más realista de la gravedad. [62]
La teoría ABJM que aparece en esta versión de la correspondencia también es interesante por diversas razones. Introducida por Aharony, Bergman, Jafferis y Maldacena, está estrechamente relacionada con otra teoría cuántica de campos llamada teoría de Chern-Simons . Esta última teoría fue popularizada por Witten a fines de la década de 1980 debido a sus aplicaciones a la teoría de nudos. [63] Además, la teoría ABJM sirve como un modelo simplificado semirrealista para resolver problemas que surgen en la física de la materia condensada. [62]

Además de ser una idea de considerable interés teórico, la teoría M proporciona un marco para construir modelos de física del mundo real que combinan la relatividad general con el modelo estándar de física de partículas . La fenomenología es la rama de la física teórica en la que los físicos construyen modelos realistas de la naturaleza a partir de ideas teóricas más abstractas. La fenomenología de cuerdas es la parte de la teoría de cuerdas que intenta construir modelos realistas de física de partículas basados en la teoría de cuerdas y la teoría M. [64]
Por lo general, estos modelos se basan en la idea de compactificación. [l] A partir del espacio-tiempo de diez u once dimensiones de la teoría de cuerdas o M, los físicos postulan una forma para las dimensiones adicionales. Al elegir esta forma apropiadamente, pueden construir modelos aproximadamente similares al modelo estándar de física de partículas, junto con partículas adicionales no descubiertas, [65] generalmente socios supersimétricos de análogos de partículas conocidas. Una forma popular de derivar física realista a partir de la teoría de cuerdas es comenzar con la teoría heterótica en diez dimensiones y asumir que las seis dimensiones adicionales del espacio-tiempo tienen la forma de una variedad de Calabi-Yau de seis dimensiones . Este es un tipo especial de objeto geométrico llamado así en honor a los matemáticos Eugenio Calabi y Shing-Tung Yau . [66] Las variedades de Calabi-Yau ofrecen muchas formas de extraer física realista de la teoría de cuerdas. Se pueden usar otros métodos similares para construir modelos con una física que se asemeje en cierta medida a la de nuestro mundo de cuatro dimensiones basado en la teoría M. [67]
En parte debido a dificultades teóricas y matemáticas y en parte debido a las energías extremadamente altas (más allá de lo que es tecnológicamente posible en el futuro previsible) necesarias para probar experimentalmente estas teorías, hasta ahora no hay evidencia experimental que indique de manera inequívoca que alguno de estos modelos sea una descripción fundamental correcta de la naturaleza. Esto ha llevado a algunos miembros de la comunidad a criticar estos enfoques de unificación y a cuestionar el valor de continuar la investigación sobre estos problemas. [68]
En una aproximación a la fenomenología de la teoría M, los teóricos suponen que las siete dimensiones adicionales de la teoría M tienen la forma de una variedad G 2 . Se trata de un tipo especial de forma de siete dimensiones construida por el matemático Dominic Joyce de la Universidad de Oxford . [69] Estas variedades G 2 todavía se entienden poco matemáticamente, y este hecho ha dificultado que los físicos desarrollen plenamente este enfoque de la fenomenología. [70]
Por ejemplo, los físicos y matemáticos a menudo suponen que el espacio tiene una propiedad matemática llamada suavidad , pero esta propiedad no se puede suponer en el caso de una variedad G 2 si uno desea recuperar la física de nuestro mundo de cuatro dimensiones. Otro problema es que las variedades G 2 no son variedades complejas , por lo que los teóricos no pueden utilizar herramientas de la rama de las matemáticas conocida como análisis complejo . Finalmente, hay muchas preguntas abiertas sobre la existencia, unicidad y otras propiedades matemáticas de las variedades G 2 , y los matemáticos carecen de una forma sistemática de buscar estas variedades. [70]
Debido a las dificultades con las variedades G 2 , la mayoría de los intentos de construir teorías realistas de la física basadas en la teoría M han adoptado un enfoque más indirecto para compactar el espacio-tiempo de once dimensiones. Un enfoque, iniciado por Witten, Hořava, Burt Ovrut y otros, se conoce como teoría M heterótica. En este enfoque, uno imagina que una de las once dimensiones de la teoría M tiene forma de círculo. Si este círculo es muy pequeño, entonces el espacio-tiempo se vuelve efectivamente decadimensional. Luego uno supone que seis de las diez dimensiones forman una variedad de Calabi-Yau. Si esta variedad de Calabi-Yau también se toma como pequeña, uno se queda con una teoría en cuatro dimensiones. [70]
La teoría M heterótica se ha utilizado para construir modelos de cosmología de branas en los que se cree que el universo observable existe en una brana en un espacio ambiental de dimensiones superiores. También ha generado teorías alternativas del universo primitivo que no se basan en la teoría de la inflación cósmica . [70]
{{cite journal}}: CS1 maint: bot: original URL status unknown (link){{cite journal}}: CS1 maint: bot: original URL status unknown (link)