Integral trigonométrica cardinal
En matemáticas, las funciones integrales trigonométricas cardinales son una familia de integrales no elementales que involucran funciones trigonométricas cardinales (aquellas que consisten en dividir una función trigonométrica en una variable, por la propia variable).
Las diferentes definiciones de la integral seno son: Téngase en cuenta que el integrando
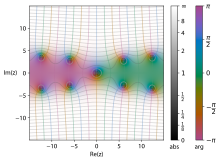
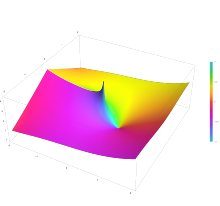
Dado que sinc es una función completa par (función holomorfa en todo el plano complejo), Si es entera, impar y para la integral de su definición se puede tomar cualquier recorrido que conecte los puntos extremos.
Las dos definiciones están relacionadas por Cin es una función completa par.
Tiene la siguiente expansión en serie: Las integrales trigonométricas se pueden entender en términos de las llamadas "funciones auxiliares": Usando estas funciones, las integrales trigonométricas se pueden reexpresar como: (cf.
[1] Se pueden utilizar varias expansiones para la evaluación de integrales trigonométricas, según el rango del argumento.
Estas series son asintóticas y divergentes, aunque pueden usarse para estimaciones e incluso evaluaciones precisas en ℜ(x) ≫ 1.
Estas series son convergentes en cualquier x complejo, aunque para |x| ≫ 1, la serie convergerá lentamente inicialmente, lo que requerirá muchos términos para obtener una alta precisión.
(2015),[2] tienen una precisión mejor que 10−16 para 0 ≤ x ≤ 4, Las integrales se pueden evaluar indirectamente mediante las funciones auxiliares