Funtor

En teoría de categorías, un funtor o functor es una función de una categoría a otra que hace corresponder objetos con objetos y morfismos con morfismos, de manera que la composición de morfismos y las identidades se preservan.Los funtores se consideraron primero en topología algebraica, donde se asocian los objetos algebraicos con los espacios topológicos y se asocian los homomorfismos algebraicos con las funciones continuas.Hoy en día, los funtores se utilizan a través de las matemáticas modernas para relacionar varias categorías.Ejemplos de functores típicos son el funtor fiel y el funtor pleno.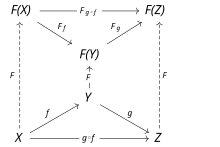Sean C y D dos categorías.Un funtor F de C a D es una correspondencia que[1]​ Es decir, los funtores deben conservar los morfismos de identidad y la composición de morfismos.Existen muchas construcciones en matemáticas que serían funtores si no fuera por el hecho de que "invierten los morfismos" e "invierten la composición".En consecuencia, se define un funtor contravariante F de C a D como una aplicación que Debe tenerse en cuenta que los funtores contravariantes invierten la dirección de la composición.Tenga en cuenta que también se puede definir un funtor contravariante como un funtor covariante en la categoría opuesta[2]​ Algunos autores prefieren escribir todas las expresiones de manera covariante.es un funtor contravariante, simplemente escribenLos funtores contravariantes también se denominan ocasionalmente cofuntores.[3]​ Existe una convención que se refiere a vectores, es decir, a campos vectoriales, elementos del espacio de secciones, como contravariantes y a covectores, es decir, 1-formas, elementos del espacio de seccionesEsta terminología se origina en la física, y su fundamento tiene que ver con la posición de los índices (arriba y abajo) en expresiones comoEn este formalismo se observa que el símbolo de transformación de coordenadas) actúa sobre las coordenadas covectoriales de la misma manera que sobre los vectores base:, mientras que actúa de manera opuesta sobre las coordenadas vectoriales (pero de la misma manera como en los covectores base:Esta terminología es contraria a la utilizada en la teoría de categorías porque son los covectores los que tienen retrocesos en general y, por tanto, son contravariantes, mientras que los vectores en general son covariantes ya que pueden ser puestos hacia adelante.Véase también covarianza y contravarianza.asigna objetos y morfismos de la misma manera quecomo categoría, y de manera similar paraTéngase en cuenta que, siguiendo la propiedad de categoría opuesta,Por ejemplo, el homomorfismo funtorial es del tipo Cop × C → Set.El homomorfismo funtorial es un ejemplo natural; es contravariante en un argumento y covariante en el otro.Un multifuntor es una generalización del concepto de funtor a n variables.Dos consecuencias importantes de la axiomática de los funtores son: Se pueden componer funtores, es decir, si F es un funtor de A a B y G es un funtor de B a C, entonces se puede formar el funtor compuesto G ∘ F de A a C. La composición de los funtores es asociativa donde se define.Una categoría pequeña con un solo objeto es lo mismo que un monoide: los morfismos de una categoría de un solo objeto pueden considerarse elementos del monoide, y la composición en la categoría se considera la operación monoide.Los funtores entre categorías de un solo objeto corresponden a homomorfismos monoides.Entonces, en cierto sentido, los funtores entre categorías arbitrarias son una especie de generalización de los homomorfismos monoides a categorías con más de un objeto.