Variedad de Riemann

Variedad lisa con un producto interno en cada espacio tangente

El producto escalar de dos vectores tangentes a la esfera que se encuentra dentro del espacio euclidiano tridimensional contiene información sobre las longitudes y los ángulos entre los vectores. Los productos escalares de cada plano tangente , agrupados en un único objeto matemático, constituyen una métrica de Riemann.

En geometría diferencial , una variedad de Riemann es un espacio geométrico en el que se definen muchas nociones geométricas como distancia, ángulos, longitud, volumen y curvatura. El espacio euclidiano , la -esfera , el espacio hiperbólico y las superficies lisas en el espacio tridimensional, como los elipsoides y los paraboloides , son ejemplos de variedades de Riemann . Las variedades de Riemann reciben su nombre del matemático alemán Bernhard Riemann , quien las conceptualizó por primera vez. ${\displaystyle n}$

Formalmente, una métrica de Riemann (o simplemente una métrica ) en una variedad suave es una elección de producto interno para cada espacio tangente de la variedad. Una variedad de Riemann es una variedad suave junto con una métrica de Riemann. Las técnicas de cálculo diferencial e integral se utilizan para extraer datos geométricos de la métrica de Riemann. Por ejemplo, la integración conduce a la función de distancia de Riemann, mientras que la diferenciación se utiliza para definir la curvatura y el transporte paralelo.

Cualquier superficie lisa en el espacio euclidiano tridimensional es una variedad riemanniana con una métrica riemanniana que proviene de la forma en que se encuentra dentro del espacio ambiente . Lo mismo es cierto para cualquier subvariedad del espacio euclidiano de cualquier dimensión. Aunque John Nash demostró que cada variedad riemanniana surge como una subvariedad del espacio euclidiano, y aunque algunas variedades riemannianas se exhiben o definen naturalmente de esa manera, la idea de una variedad riemanniana enfatiza el punto de vista intrínseco, que define nociones geométricas directamente en el espacio abstracto en sí mismo sin hacer referencia a un espacio ambiente. En muchos casos, como para el espacio hiperbólico y el espacio proyectivo , las métricas riemannianas se definen o construyen de manera más natural utilizando el punto de vista intrínseco. Además, muchas métricas en grupos de Lie y espacios homogéneos se definen intrínsecamente mediante el uso de acciones de grupo para transportar un producto interno en un solo espacio tangente a toda la variedad, y muchas métricas especiales, como las métricas de curvatura escalar constante y las métricas de Kähler-Einstein, se construyen intrínsecamente utilizando herramientas de ecuaciones diferenciales parciales .

La geometría de Riemann , el estudio de las variedades de Riemann, tiene profundas conexiones con otras áreas de las matemáticas, incluyendo la topología geométrica , la geometría compleja y la geometría algebraica . Las aplicaciones incluyen la física (especialmente la relatividad general y la teoría de calibre ), los gráficos por computadora , el aprendizaje automático y la cartografía . Las generalizaciones de las variedades de Riemann incluyen las variedades pseudo-riemannianas , las variedades de Finsler y las variedades sub-riemannianas .

Historia

Las variedades de Riemann fueron conceptualizadas por primera vez por su homónimo, el matemático alemán Bernhard Riemann .

En 1827, Carl Friedrich Gauss descubrió que la curvatura gaussiana de una superficie incrustada en el espacio tridimensional sólo depende de mediciones locales realizadas dentro de la superficie (la primera forma fundamental ). ^[1] Este resultado se conoce como Theorema Egregium ("teorema notable" en latín).

Un mapa que preserva las medidas locales de una superficie se denomina isometría local . Llamemos a una propiedad de una superficie una propiedad intrínseca si se preserva mediante isometrías locales y una propiedad extrínseca si no lo hace. En este lenguaje, el Teorema Egregium dice que la curvatura gaussiana es una propiedad intrínseca de las superficies.

Las variedades de Riemann y su curvatura fueron introducidas por primera vez de manera no rigurosa por Bernhard Riemann en 1854. ^[2] Sin embargo, no se formalizarían hasta mucho después. De hecho, el concepto más primitivo de una variedad suave fue definido explícitamente por primera vez recién en 1913 en un libro de Hermann Weyl . ^[2]

Élie Cartan introdujo la conexión de Cartan , uno de los primeros conceptos de conexión . Levi-Civita definió la conexión de Levi-Civita , una conexión especial en una variedad de Riemann.

Albert Einstein utilizó la teoría de las variedades pseudo-riemannianas (una generalización de las variedades riemannianas) para desarrollar la relatividad general . En concreto, las ecuaciones de campo de Einstein son restricciones sobre la curvatura del espacio-tiempo , que es una variedad pseudo-riemanniana de cuatro dimensiones.

Definición

Métricas de Riemann y variedades de Riemann

Plano tangente de la esfera con dos vectores en él. Una métrica de Riemann permite obtener el producto interno de estos vectores.

Sea una variedad suave . Para cada punto , hay un espacio vectorial asociado llamado espacio tangente de en . Los vectores en se consideran vectores tangentes a en . ${\displaystyle M}$ ${\displaystyle p\in M}$ ${\displaystyle T_{p}M}$ ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle T_{p}M}$ ${\displaystyle M}$ ${\displaystyle p}$

Sin embargo, no viene equipado con un producto interno , una vara de medir que proporcione a los vectores tangentes un concepto de longitud y ángulo. Esta es una deficiencia importante porque el cálculo enseña que para calcular la longitud de una curva, se debe definir la longitud de los vectores tangentes a la curva. Una métrica de Riemann pone una vara de medir en cada espacio tangente. ${\displaystyle T_{p}M}$

Una métrica riemanniana en asigna a cada uno un producto interno positivo definido de manera uniforme (ver la sección sobre regularidad a continuación). ^[3] Esto induce una norma definida por . Una variedad uniforme dotada de una métrica riemanniana es una variedad riemanniana , denotada . ^[3] Una métrica riemanniana es un caso especial de un tensor métrico . ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle g_{p}:T_{p}M\times T_{p}M\to \mathbb {R} }$ ${\displaystyle \|\cdot \|_{p}:T_{p}M\to \mathbb {R} }$ ${\displaystyle \|v\|_{p}={\sqrt {g_{p}(v,v)}}}$ ${\displaystyle M}$ ${\displaystyle g}$ ${\displaystyle (M,g)}$

Una métrica de Riemann no debe confundirse con la función de distancia de un espacio métrico , también llamada métrica.

La métrica de Riemann en coordenadas

Si son coordenadas locales suaves en , los vectores ${\displaystyle (x^{1},\ldots ,x^{n}):U\to \mathbb {R} ^{n}}$ ${\displaystyle M}$

${\displaystyle \left\{{\frac {\partial }{\partial x^{1}}}{\Big |}_{p},\dotsc ,{\frac {\partial }{\partial x^{n}}}{\Big |}_{p}\right\}}$

forman una base del espacio vectorial para cualquier . Con relación a esta base, se pueden definir los componentes de la métrica de Riemann en cada punto mediante ${\displaystyle T_{p}M}$ ${\displaystyle p\in U}$ ${\displaystyle p}$

${\displaystyle g_{ij}|_{p}:=g_{p}\left(\left.{\frac {\partial }{\partial x^{i}}}\right|_{p},\left.{\frac {\partial }{\partial x^{j}}}\right|_{p}\right)}$. ^[4]

Estas funciones se pueden agrupar en una función matricial en . El requisito de que sea un producto interno positivo-definido dice exactamente que esta función matricial es una matriz positiva-definida simétrica en . ${\displaystyle n^{2}}$ ${\displaystyle g_{ij}:U\to \mathbb {R} }$ ${\displaystyle n\times n}$ ${\displaystyle U}$ ${\displaystyle g_{p}}$ ${\displaystyle p}$

En términos del álgebra tensorial , la métrica de Riemann se puede escribir en términos de la base dual del fibrado cotangente como ${\displaystyle \{dx^{1},\ldots ,dx^{n}\}}$

${\displaystyle g=\sum _{i,j}g_{ij}\,dx^{i}\otimes dx^{j}.}$^[4]

Regularidad de la métrica de Riemann

La métrica de Riemann es continua si sus componentes son continuos en cualquier diagrama de coordenadas suaves . La métrica de Riemann es suave si sus componentes son suaves en cualquier diagrama de coordenadas suaves. Se pueden considerar muchos otros tipos de métricas de Riemann en este espíritu, como las métricas de Riemann de Lipschitz o las métricas de Riemann medibles . ${\displaystyle g}$ ${\displaystyle g_{ij}:U\to \mathbb {R} }$ ${\displaystyle (U,x).}$ ${\displaystyle g}$ ${\displaystyle g_{ij}}$

Existen situaciones en el análisis geométrico en las que se desea considerar métricas de Riemann no uniformes. Véase, por ejemplo, (Gromov 1999) y (Shi y Tam 2002). Sin embargo, en este artículo, se supone que es uniforme a menos que se indique lo contrario. ${\displaystyle g}$

Isomorfismo musical

En analogía a cómo un producto interno en un espacio vectorial induce un isomorfismo entre un espacio vectorial y su dual dado por , una métrica de Riemann induce un isomorfismo de fibrados entre el fibrado tangente y el fibrado cotangente . Es decir, si es una métrica de Riemann, entonces ${\displaystyle v\mapsto \langle v,\cdot \rangle }$ ${\displaystyle g}$

${\displaystyle (p,v)\mapsto g_{p}(v,\cdot )}$

es un isomorfismo de fibrados vectoriales suaves desde el fibrado tangente hasta el fibrado cotangente . ^[5] ${\displaystyle TM}$ ${\displaystyle T^{*}M}$

Isometrías

Una isometría es una función entre variedades de Riemann que conserva toda la estructura de las variedades de Riemann. Si dos variedades de Riemann tienen una isometría entre ellas, se denominan isométricas y se consideran la misma variedad a los efectos de la geometría de Riemann.

En concreto, si y son dos variedades de Riemann, un difeomorfismo se denomina isometría si , ^[6] es decir, si ${\displaystyle (M,g)}$ ${\displaystyle (N,h)}$ ${\displaystyle f:M\to N}$ ${\displaystyle g=f^{\ast }h}$

${\displaystyle g_{p}(u,v)=h_{f(p)}(df_{p}(u),df_{p}(v))}$

para todos y Por ejemplo, las traslaciones y rotaciones son ambas isometrías del espacio euclidiano (que se definirá pronto) hacia sí mismo. ${\displaystyle p\in M}$ ${\displaystyle u,v\in T_{p}M.}$

Se dice que una función suave que no se supone que sea un difeomorfismo es una isometría local si cada una tiene un vecindario abierto tal que es una isometría (y por lo tanto un difeomorfismo). ^[6] ${\displaystyle f:M\to N,}$ ${\displaystyle p\in M}$ ${\displaystyle U}$ ${\displaystyle f:U\to f(U)}$

Volumen

Una variedad de Riemann orientada -dimensional tiene una única forma llamada forma de volumen de Riemann . ^[7] La ​​forma de volumen de Riemann se conserva mediante isometrías que preservan la orientación. ^[8] La forma de volumen da lugar a una medida en la que permite integrar funciones mensurables. ^{[ cita requerida ]} Si es compacto , el volumen de es . ^[7] ${\displaystyle n}$ ${\displaystyle (M,g)}$ ${\displaystyle n}$ ${\displaystyle dV_{g}}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \int _{M}dV_{g}}$

Ejemplos

Espacio euclidiano

Sea que las coordenadas estándar sean la métrica euclidiana (canónica) se dan por ^[9] ${\displaystyle x^{1},\ldots ,x^{n}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle g^{\text{can}}}$

${\displaystyle g^{\text{can}}\left(\sum _{i}a_{i}{\frac {\partial }{\partial x^{i}}},\sum _{j}b_{j}{\frac {\partial }{\partial x^{j}}}\right)=\sum _{i}a_{i}b_{i}}$

o equivalentemente

${\displaystyle g^{\text{can}}=(dx^{1})^{2}+\cdots +(dx^{n})^{2}}$

o equivalentemente por sus funciones de coordenadas

${\displaystyle g_{ij}^{\text{can}}=\delta _{ij}}$¿Dónde está el delta de Kronecker? ${\displaystyle \delta _{ij}}$

que juntos forman la matriz

${\displaystyle (g_{ij}^{\text{can}})={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}.}$

La variedad de Riemann se llama espacio euclidiano . ${\displaystyle (\mathbb {R} ^{n},g^{\text{can}})}$

Subvariedades

La -esfera con métrica redonda es una subvariedad riemanniana incorporada de . ${\displaystyle n}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} ^{n+1}}$

Sea una variedad de Riemann y sea una subvariedad inmersa o una subvariedad incrustada de . El pullback de es una métrica de Riemann en , y se dice que es una subvariedad de Riemann de . ^[10] ${\displaystyle (M,g)}$ ${\displaystyle i:N\to M}$ ${\displaystyle M}$ ${\displaystyle i^{*}g}$ ${\displaystyle g}$ ${\displaystyle N}$ ${\displaystyle (N,i^{*}g)}$ ${\displaystyle (M,g)}$

En el caso en que , la función está dada por y la métrica es simplemente la restricción de a vectores tangentes a lo largo de . En general, la fórmula para es ${\displaystyle N\subseteq M}$ ${\displaystyle i:N\to M}$ ${\displaystyle i(x)=x}$ ${\displaystyle i^{*}g}$ ${\displaystyle g}$ ${\displaystyle N}$ ${\displaystyle i^{*}g}$

${\displaystyle i^{*}g_{p}(v,w)=g_{i(p)}{\big (}di_{p}(v),di_{p}(w){\big )},}$

¿Dónde está el impulso hacia adelante de por? ${\displaystyle di_{p}(v)}$ ${\displaystyle v}$ ${\displaystyle i.}$

Ejemplos:

• La -esfera ${\displaystyle n}$

  ${\displaystyle S^{n}=\{x\in \mathbb {R} ^{n+1}:(x^{1})^{2}+\cdots +(x^{n+1})^{2}=1\}}$

es una subvariedad incrustada suave del espacio euclidiano . ^[11] La métrica de Riemann que esto induce se llama métrica redonda o métrica estándar . ${\displaystyle \mathbb {R} ^{n+1}}$ ${\displaystyle S^{n}}$

• Arreglar números reales . El elipsoide ${\displaystyle a,b,c}$

  ${\displaystyle \left\{x\in \mathbb {R} ^{3}:{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\right\}}$

es una subvariedad incrustada suave del espacio euclidiano . ${\displaystyle \mathbb {R} ^{3}}$

• La gráfica de una función suave es una subvariedad suave incrustada con su métrica estándar. ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{n+1}}$
• Si no es simplemente conexo, existe una función de recubrimiento , donde es el recubrimiento universal de . Esto es una inmersión (ya que es localmente un difeomorfismo), por lo que hereda automáticamente una métrica de Riemann. Por el mismo principio, cualquier espacio de recubrimiento suave de una variedad de Riemann hereda una métrica de Riemann. ${\displaystyle (M,g)}$ ${\displaystyle {\widetilde {M}}\to M}$ ${\displaystyle {\widetilde {M}}}$ ${\displaystyle M}$ ${\displaystyle {\widetilde {M}}}$

Por otra parte, si ya tiene una métrica riemanniana , entonces la inmersión (o incrustación) se llama inmersión isométrica (o incrustación isométrica ) si . Por lo tanto, las inmersiones isométricas y las incrustaciones isométricas son subvariedades riemannianas. ^[10] ${\displaystyle N}$ ${\displaystyle {\tilde {g}}}$ ${\displaystyle i:N\to M}$ ${\displaystyle {\tilde {g}}=i^{*}g}$

Productos

Un toro lleva naturalmente una métrica euclidiana, obtenida al identificar los lados opuestos de un cuadrado (izquierda). La variedad de Riemann resultante, llamada toro plano , no se puede incrustar isométricamente en el espacio euclidiano tridimensional (derecha), porque es necesario doblar y estirar la lámina para hacerlo. Por lo tanto, la geometría intrínseca de un toro plano es diferente de la de un toro incrustado.

Sean y dos variedades de Riemann y considere la variedad producto . Las métricas de Riemann y naturalmente ponen una métrica de Riemann en la que se puede describir de varias maneras. ${\displaystyle (M,g)}$ ${\displaystyle (N,h)}$ ${\displaystyle M\times N}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle {\widetilde {g}}}$ ${\displaystyle M\times N,}$

• Considerando la descomposición se puede definir ${\displaystyle T_{(p,q)}(M\times N)\cong T_{p}M\oplus T_{q}N,}$

  ${\displaystyle {\widetilde {g}}_{p,q}((u_{1},u_{2}),(v_{1},v_{2}))=g_{p}(u_{1},v_{1})+h_{q}(u_{2},v_{2}).}$^[12]

• Si es un gráfico de coordenadas suaves en y es un gráfico de coordenadas suaves en , entonces es un gráfico de coordenadas suaves en Sea la representación de en el gráfico y sea la representación de en el gráfico . La representación de en las coordenadas es ${\displaystyle (U,x)}$ ${\displaystyle M}$ ${\displaystyle (V,y)}$ ${\displaystyle N}$ ${\displaystyle (U\times V,(x,y))}$ ${\displaystyle M\times N.}$ ${\displaystyle g_{U}}$ ${\displaystyle g}$ ${\displaystyle (U,x)}$ ${\displaystyle h_{V}}$ ${\displaystyle h}$ ${\displaystyle (V,y)}$ ${\displaystyle {\widetilde {g}}}$ ${\displaystyle (U\times V,(x,y))}$

  ${\displaystyle {\widetilde {g}}=\sum _{ij}{\widetilde {g}}_{ij}\,dx^{i}\,dx^{j}}$donde ^[12] ${\displaystyle ({\widetilde {g}}_{ij})={\begin{pmatrix}g_{U}&0\\0&h_{V}\end{pmatrix}}.}$

Por ejemplo, considere el -toro . Si a cada copia de se le da la métrica redonda, la variedad de Riemann producto se llama toro plano . Como otro ejemplo, el producto de Riemann , donde cada copia de tiene la métrica euclidiana, es isométrico a con la métrica euclidiana. ${\displaystyle n}$ ${\displaystyle T^{n}=S^{1}\times \cdots \times S^{1}}$ ${\displaystyle S^{1}}$ ${\displaystyle T^{n}}$ ${\displaystyle \mathbb {R} \times \cdots \times \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{n}}$

Combinaciones positivas de métricas

Sean métricas de Riemann en Si hay funciones suaves positivas en , entonces es otra métrica de Riemann en ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle M.}$ ${\displaystyle f_{1},\ldots ,f_{k}}$ ${\displaystyle M}$ ${\displaystyle f_{1}g_{1}+\ldots +f_{k}g_{k}}$ ${\displaystyle M.}$

Toda variedad suave admite una métrica de Riemann

Teorema: Toda variedad suave admite una métrica riemanniana (no canónica). ^[13]

Este es un resultado fundamental. Aunque gran parte de la teoría básica de las métricas de Riemann se puede desarrollar utilizando únicamente el supuesto de que una variedad suave es un espacio topológico localmente euclidiano, para este resultado es necesario utilizar el supuesto de que las variedades suaves son Hausdorff y paracompactas . La razón es que la prueba hace uso de una partición de la unidad .

Una prueba alternativa utiliza el teorema de incrustación de Whitney para incrustar en el espacio euclidiano y luego retira la métrica del espacio euclidiano a . Por otro lado, el teorema de incrustación de Nash establece que, dada cualquier variedad riemanniana suave, existe una incrustación para algún tal que el retiro por de la métrica riemanniana estándar en es Es decir, la estructura completa de una variedad riemanniana suave puede codificarse por un difeomorfismo a una cierta subvariedad incrustada de algún espacio euclidiano. Por lo tanto, se podría argumentar que nada se puede ganar de la consideración de variedades abstractas suaves y sus métricas riemannianas. Sin embargo, hay muchas variedades riemannianas suaves naturales, como el conjunto de rotaciones del espacio tridimensional y el espacio hiperbólico, de las cuales cualquier representación como una subvariedad del espacio euclidiano no representará sus notables simetrías y propiedades tan claramente como lo hacen sus presentaciones abstractas. ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle (M,g),}$ ${\displaystyle F:M\to \mathbb {R} ^{N}}$ ${\displaystyle N}$ ${\displaystyle F}$ ${\displaystyle \mathbb {R} ^{N}}$ ${\displaystyle g.}$

Estructura del espacio métrico

Una curva admisible es una curva suave por partes cuya velocidad es distinta de cero en todos los lugares donde está definida. La función no negativa está definida en el intervalo, excepto en un número finito de puntos. La longitud de una curva admisible se define como ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma '(t)\in T_{\gamma (t)}M}$ ${\displaystyle t\mapsto \|\gamma '(t)\|_{\gamma (t)}}$ ${\displaystyle [0,1]}$ ${\displaystyle L(\gamma )}$ ${\displaystyle \gamma :[0,1]\to M}$

${\displaystyle L(\gamma )=\int _{0}^{1}\|\gamma '(t)\|_{\gamma (t)}\,dt.}$

El integrando está acotado y es continuo excepto en un número finito de puntos, por lo que es integrable. Para una variedad de Riemann conexa, defina por ${\displaystyle (M,g)}$ ${\displaystyle d_{g}:M\times M\to [0,\infty )}$

${\displaystyle d_{g}(p,q)=\inf\{L(\gamma ):\gamma {\text{ an admissible curve with }}\gamma (0)=p,\gamma (1)=q\}.}$

Teorema: es un espacio métrico , y la topología métrica en coincide con la topología en . ^[14] ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle M}$

Aunque la longitud de una curva se da mediante una fórmula explícita, generalmente es imposible escribir la función de distancia por cualquier medio explícito. De hecho, si es compacto, siempre existen puntos donde es no diferenciable, y puede ser notablemente difícil incluso determinar la ubicación o la naturaleza de estos puntos, incluso en casos aparentemente simples como cuando es un elipsoide. ^{[ cita requerida ]} ${\displaystyle d_{g}}$ ${\displaystyle M}$ ${\displaystyle d_{g}:M\times M\to \mathbb {R} }$ ${\displaystyle (M,g)}$

Si se trabaja con métricas de Riemann que son meramente continuas pero posiblemente no suaves, la longitud de una curva admisible y la función de distancia de Riemann se definen exactamente de la misma manera y, como antes, es un espacio métrico y la topología métrica en coincide con la topología en . ^[15] ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle M}$

Diámetro

El diámetro del espacio métrico es ${\displaystyle (M,d_{g})}$

${\displaystyle \operatorname {diam} (M,d_{g})=\sup\{d_{g}(p,q):p,q\in M\}.}$

El teorema de Hopf-Rinow demuestra que si es completa y tiene diámetro finito, es compacta. Por el contrario, si es compacta, entonces la función tiene un máximo, ya que es una función continua en un espacio métrico compacto. Esto demuestra lo siguiente. ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle d_{g}:M\times M\to \mathbb {R} }$

Si es completo, entonces es compacto si y sólo si tiene diámetro finito. ${\displaystyle (M,d_{g})}$

Esto no es así sin el supuesto de completitud; como contraejemplo se podría considerar cualquier subconjunto abierto y acotado de un espacio euclidiano con la métrica riemanniana estándar. Tampoco es cierto que cualquier espacio métrico completo de diámetro finito deba ser compacto; lo que importa es que el espacio métrico provenga de una variedad riemanniana.

Conexiones, geodésicas y curvatura

Conexiones

Una conexión (afín) es una estructura adicional en una variedad de Riemann que define la diferenciación de un campo vectorial con respecto a otro. Las conexiones contienen datos geométricos y dos variedades de Riemann con diferentes conexiones tienen geometrías diferentes.

Sea el espacio de campos vectoriales en . Una conexión (afín) ${\displaystyle {\mathfrak {X}}(M)}$ ${\displaystyle M}$

${\displaystyle \nabla :{\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\to {\mathfrak {X}}(M)}$

on es un mapa bilineal tal que ${\displaystyle M}$ ${\displaystyle (X,Y)\mapsto \nabla _{X}Y}$

1. Para cada función , ${\displaystyle f\in C^{\infty }(M)}$ ${\displaystyle \nabla _{f_{1}X_{1}+f_{2}X_{2}}Y=f_{1}\,\nabla _{X_{1}}Y+f_{2}\,\nabla _{X_{2}}Y,}$
2. La regla del producto se cumple. ^[16] ${\displaystyle \nabla _{X}fY=X(f)Y+f\,\nabla _{X}Y}$

La expresión se llama derivada covariante de con respecto a . ${\displaystyle \nabla _{X}Y}$ ${\displaystyle Y}$ ${\displaystyle X}$

Conexión Levi-Civita

Dos variedades de Riemann con diferentes conexiones tienen geometrías diferentes. Afortunadamente, existe una conexión natural asociada a una variedad de Riemann llamada conexión de Levi-Civita .

Se dice que una conexión preserva la métrica si ${\displaystyle \nabla }$

${\displaystyle X{\bigl (}g(Y,Z){\bigr )}=g(\nabla _{X}Y,Z)+g(Y,\nabla _{X}Z)}$

Una conexión está libre de torsión si ${\displaystyle \nabla }$

${\displaystyle \nabla _{X}Y-\nabla _{Y}X=[X,Y],}$

¿Dónde está el corchete de Lie ? ${\displaystyle [\cdot ,\cdot ]}$

Una conexión de Levi-Civita es una conexión libre de torsión que preserva la métrica. Una vez que se fija una métrica de Riemann, existe una conexión de Levi-Civita única. ^[17] Nótese que la definición de preservación de la métrica utiliza la regularidad de . ${\displaystyle g}$

Derivada covariante a lo largo de una curva

Si es una curva suave, un campo vectorial suave a lo largo de es una función suave tal que para todo . El conjunto de campos vectoriales suaves a lo largo de es un espacio vectorial bajo la suma de vectores puntual y la multiplicación escalar. ^[18] También se puede multiplicar puntualmente un campo vectorial suave a lo largo de por una función suave : ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$ ${\displaystyle X:[0,1]\to TM}$ ${\displaystyle X(t)\in T_{\gamma (t)}M}$ ${\displaystyle t\in [0,1]}$ ${\displaystyle {\mathfrak {X}}(\gamma )}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle f:[0,1]\to \mathbb {R} }$

${\displaystyle (fX)(t)=f(t)X(t)}$para ${\displaystyle X\in {\mathfrak {X}}(\gamma ).}$

Sea un campo vectorial suave a lo largo de . Si es un campo vectorial suave en un entorno de la imagen de tal que , entonces se denomina extensión de . ${\displaystyle X}$ ${\displaystyle \gamma }$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle \gamma }$ ${\displaystyle X(t)={\tilde {X}}_{\gamma (t)}}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle X}$

Dada una conexión fija en y una curva suave , existe un operador único , llamado derivada covariante a lo largo de , tal que: ^[19] ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle D_{t}:{\mathfrak {X}}(\gamma )\to {\mathfrak {X}}(\gamma )}$ ${\displaystyle \gamma }$

1. ${\displaystyle D_{t}(aX+bY)=a\,D_{t}X+b\,D_{t}Y,}$
2. ${\displaystyle D_{t}(fX)=f'X+f\,D_{t}X,}$
3. Si es una extensión de , entonces . ${\displaystyle {\tilde {X}}}$ ${\displaystyle X}$ ${\displaystyle D_{t}X(t)=\nabla _{\gamma '(t)}{\tilde {X}}}$

Geodésicas

En el espacio euclidiano (izquierda), las geodésicas máximas son líneas rectas. En la esfera redonda (derecha), las geodésicas máximas son círculos máximos . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S^{n}}$

Las geodésicas son curvas sin aceleración intrínseca. De manera equivalente, las geodésicas son curvas que localmente toman el camino más corto entre dos puntos. Son la generalización de las líneas rectas en el espacio euclidiano a variedades riemannianas arbitrarias. Una hormiga que viva en una variedad riemanniana caminando en línea recta sin hacer ningún esfuerzo por acelerar o girar trazaría una geodésica.

Fijemos una conexión en . Sea una curva suave. La aceleración de es el campo vectorial a lo largo de . Si para todo , se denomina geodésica . ^[20] ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}\gamma '}$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}\gamma '=0}$ ${\displaystyle t}$ ${\displaystyle \gamma }$

Para cada y , existe una geodésica definida en algún intervalo abierto que contiene 0 tal que y . Cualesquiera dos de estas geodésicas concuerdan en su dominio común. ^[21] Tomando la unión sobre todos los intervalos abiertos que contienen 0 en los que existe una geodésica que satisface y , se obtiene una geodésica llamada geodésica máxima de la cual toda geodésica que satisface y es una restricción. ^[22] ${\displaystyle p\in M}$ ${\displaystyle v\in T_{p}M}$ ${\displaystyle \gamma :I\to M}$ ${\displaystyle I}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$ ${\displaystyle I}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$

Toda curva que tenga la longitud más corta de cualquier curva admisible con los mismos puntos finales es una geodésica (en una reparametrización de velocidad unitaria). ^[23] ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$

Ejemplos

• Las geodésicas máximas no constantes del plano euclidiano son exactamente las líneas rectas. ^[22] Esto concuerda con el hecho de la geometría euclidiana de que el camino más corto entre dos puntos es un segmento de línea recta. ${\displaystyle \mathbb {R} ^{2}}$
• Las geodésicas máximas no constantes de con la métrica redonda son exactamente los círculos máximos . ^[24] Dado que la Tierra es aproximadamente una esfera, esto significa que el camino más corto que un avión puede recorrer entre dos ubicaciones en la Tierra es un segmento de un círculo máximo. ${\displaystyle S^{2}}$

Teorema de Hopf-Rinow

El plano perforado no es geodésicamente completo porque la geodésica máxima con condiciones iniciales , no tiene dominio . ${\displaystyle \mathbb {R} ^{2}\backslash \{(0,0)\}}$ ${\displaystyle p=(1,1)}$ ${\displaystyle v=(1,1)}$ ${\displaystyle \mathbb {R} }$

La variedad riemanniana con su conexión de Levi-Civita es geodésicamente completa si el dominio de cada geodésica máxima es . ^[25] El plano es geodésicamente completo. Por otra parte, el plano perforado con la restricción de la métrica riemanniana de no es geodésicamente completo ya que la geodésica máxima con condiciones iniciales , no tiene dominio . ${\displaystyle M}$ ${\displaystyle (-\infty ,\infty )}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{2}\smallsetminus \{(0,0)\}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle p=(1,1)}$ ${\displaystyle v=(1,1)}$ ${\displaystyle \mathbb {R} }$

El teorema de Hopf-Rinow caracteriza variedades geodésicamente completas.

Teorema: Sea una variedad riemanniana conexa. Las siguientes son equivalentes: ^[26] ${\displaystyle (M,g)}$

• El espacio métrico es completo (toda secuencia de Cauchy converge), ${\displaystyle (M,d_{g})}$ ${\displaystyle d_{g}}$
• Todos los subconjuntos cerrados y acotados de son compactos, ${\displaystyle M}$
• ${\displaystyle M}$es geodésicamente completo.

Transporte paralelo

Transporte paralelo de un vector tangente a lo largo de una curva en la esfera.

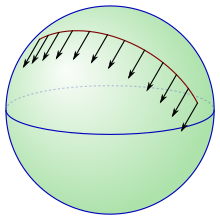
En el espacio euclidiano, todos los espacios tangentes se identifican canónicamente entre sí mediante la traslación, por lo que es fácil mover vectores de un espacio tangente a otro. El transporte paralelo es una forma de mover vectores de un espacio tangente a otro a lo largo de una curva en el contexto de una variedad riemanniana general. Dada una conexión fija, existe una única forma de realizar el transporte paralelo. ^[27]

En concreto, llamamos a un campo vectorial suave a lo largo de una curva suave paralela a lo largo de si son idénticas. ^[22] Fija una curva con y . para transportar en paralelo un vector a un vector en a lo largo de , primero extiende a un campo vectorial paralelo a lo largo de , y luego toma el valor de este campo vectorial en . ${\displaystyle V}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}V=0}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma (1)=q}$ ${\displaystyle v\in T_{p}M}$ ${\displaystyle T_{q}M}$ ${\displaystyle \gamma }$ ${\displaystyle v}$ ${\displaystyle \gamma }$ ${\displaystyle q}$

Las imágenes a continuación muestran el transporte paralelo inducido por la conexión de Levi-Civita asociada a dos métricas de Riemann diferentes en el plano perforado . La curva a lo largo de la cual se realiza el transporte paralelo es el círculo unitario. En coordenadas polares , la métrica de la izquierda es la métrica euclidiana estándar , mientras que la métrica de la derecha es . Esta segunda métrica tiene una singularidad en el origen, por lo que no se extiende más allá de la perforación, pero la primera métrica se extiende a todo el plano. ${\displaystyle \mathbb {R} ^{2}\smallsetminus \{0,0\}}$ ${\displaystyle dx^{2}+dy^{2}=dr^{2}+r^{2}\,d\theta ^{2}}$ ${\displaystyle dr^{2}+d\theta ^{2}}$

Transportes paralelos en el plano perforado bajo conexiones Levi-Civita

Advertencia: Se trata de un transporte paralelo en el plano perforado a lo largo del círculo unitario, no de un transporte paralelo en el círculo unitario. De hecho, en la primera imagen, los vectores quedan fuera del espacio tangente al círculo unitario.

Tensor de curvatura de Riemann

El tensor de curvatura de Riemann mide con precisión hasta qué punto los vectores transportadores paralelos alrededor de un pequeño rectángulo no son el mapa identidad. ^[28] El tensor de curvatura de Riemann es 0 en cada punto si y solo si la variedad es localmente isométrica al espacio euclidiano. ^[29]

Fije una conexión en . El tensor de curvatura de Riemann es el mapa definido por ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle R:{\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\to {\mathfrak {X}}(M)}$

${\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z}$

donde es el corchete de Lie de los campos vectoriales . El tensor de curvatura de Riemann es un campo tensorial . ^[30] ${\displaystyle [X,Y]}$ ${\displaystyle (1,3)}$

Tensor de curvatura de Ricci

Fije una conexión en . El tensor de curvatura de Ricci es ${\displaystyle \nabla }$ ${\displaystyle M}$

${\displaystyle Ric(X,Y)=\operatorname {tr} (Z\mapsto R(Z,X)Y)}$

donde está la traza. El tensor de curvatura de Ricci es un campo covariante de 2 tensores. ^[31] ${\displaystyle \operatorname {tr} }$

Variedades de Einstein

El tensor de curvatura de Ricci desempeña un papel determinante en la teoría de las variedades de Einstein , que tiene aplicaciones en el estudio de la gravedad . Una métrica (pseudo)riemanniana se denomina métrica de Einstein si la ecuación de Einstein ${\displaystyle Ric}$ ${\displaystyle g}$

${\displaystyle Ric=\lambda g}$Por alguna constante ${\displaystyle \lambda }$

se cumple, y una variedad (pseudo-)riemanniana cuya métrica es Einstein se llama variedad de Einstein . ^[32] Los ejemplos de variedades de Einstein incluyen el espacio euclidiano, la -esfera, el espacio hiperbólico y el espacio proyectivo complejo con la métrica de Fubini-Study . ${\displaystyle n}$

Curvatura escalar

Curvatura constante y formas espaciales.

Se dice que una variedad de Riemann tiene una curvatura constante κ si cada curvatura seccional es igual al número κ . Esto es equivalente a la condición de que, en relación con cualquier gráfico de coordenadas, el tensor de curvatura de Riemann se puede expresar en términos del tensor métrico como

${\displaystyle R_{ijkl}=\kappa (g_{il}g_{jk}-g_{ik}g_{jl}).}$

Esto implica que la curvatura de Ricci está dada por R _jk = ( n – 1) κg _jk y la curvatura escalar es n ( n – 1) κ , donde n es la dimensión de la variedad. En particular, cada variedad de Riemann de curvatura constante es una variedad de Einstein , por lo que tiene una curvatura escalar constante. Como descubrió Bernhard Riemann en su conferencia de 1854 introduciendo la geometría de Riemann, la métrica de Riemann definida localmente

${\displaystyle {\frac {dx_{1}^{2}+\cdots +dx_{n}^{2}}{(1+{\frac {\kappa }{4}}(x_{1}^{2}+\cdots +x_{n}^{2}))^{2}}}}$

tiene una curvatura constante κ . Dos variedades riemannianas cualesquiera de la misma curvatura constante son localmente isométricas , y por lo tanto se deduce que cualquier variedad riemanniana de curvatura constante κ puede ser cubierta por gráficos de coordenadas en relación con los cuales la métrica tiene la forma anterior. ^[33]

Una forma espacial de Riemann es una variedad de Riemann con curvatura constante que además es conexa y geodésicamente completa . Se dice que una forma espacial de Riemann es una forma espacial esférica si la curvatura es positiva, una forma espacial euclidiana si la curvatura es cero y una forma espacial hiperbólica o variedad hiperbólica si la curvatura es negativa. En cualquier dimensión, la esfera con su métrica riemanniana estándar, el espacio euclidiano y el espacio hiperbólico son formas espaciales de Riemann de curvatura constante 1 , 0 y –1 respectivamente. Además, el teorema de Killing-Hopf dice que cualquier forma espacial esférica simplemente conexa es homotética a la esfera, cualquier forma espacial euclidiana simplemente conexa es homotética al espacio euclidiano y cualquier forma espacial hiperbólica simplemente conexa es homotética al espacio hiperbólico. ^[33]

Utilizando la construcción de la variedad cubriente , cualquier forma espacial de Riemann es isométrica a la variedad cociente de una forma espacial de Riemann simplemente conexa, módulo una cierta acción de grupo de isometrías. Por ejemplo, el grupo de isometría de la n -esfera es el grupo ortogonal O( n + 1) . Dado cualquier subgrupo finito G de la misma en el que solo la matriz identidad posee 1 como valor propio , la acción de grupo natural del grupo ortogonal sobre la n -esfera se restringe a una acción de grupo de G , con la variedad cociente S ⁿ / G heredando una métrica de Riemann geodésicamente completa de curvatura constante 1 . Hasta la homotecia, toda forma espacial esférica surge de esta manera; esto reduce en gran medida el estudio de las formas espaciales esféricas a problemas de teoría de grupos . Por ejemplo, esto se puede utilizar para mostrar directamente que toda forma espacial esférica de dimensión par es homotética a la métrica estándar en la esfera o en el espacio proyectivo real . Existen muchas más formas espaciales esféricas de dimensiones impares, aunque existen algoritmos conocidos para su clasificación. La lista de formas espaciales esféricas tridimensionales es infinita pero conocida explícitamente, e incluye los espacios de lentes y el espacio dodecaédrico de Poincaré . ^[34]

El caso de las formas espaciales euclidianas e hiperbólicas puede reducirse asimismo a la teoría de grupos, basada en el estudio del grupo de isometría del espacio euclidiano y del espacio hiperbólico. Por ejemplo, la clase de formas espaciales euclidianas bidimensionales incluye métricas de Riemann en la botella de Klein , la banda de Möbius , el toro , el cilindro S ¹ × ℝ , junto con el plano euclidiano. A diferencia del caso de las formas espaciales esféricas bidimensionales, en algunos casos dos estructuras de formas espaciales en la misma variedad no son homotéticas. El caso de las formas espaciales hiperbólicas bidimensionales es aún más complicado, y tiene que ver con el espacio de Teichmüller . En tres dimensiones, se conocen las formas espaciales euclidianas, mientras que la geometría de las formas espaciales hiperbólicas en tres dimensiones y dimensiones superiores sigue siendo un área de investigación activa conocida como geometría hiperbólica . ^[35]

Métricas de Riemann sobre grupos de Lie

Métricas invariantes a la izquierda en grupos de Lie

Sea G un grupo de Lie , como el grupo de rotaciones en el espacio tridimensional . Utilizando la estructura de grupo, cualquier producto interno en el espacio tangente en la identidad (o cualquier otro espacio tangente particular) puede transportarse a todos los demás espacios tangentes para definir una métrica de Riemann. Formalmente, dado un producto interno g _e en el espacio tangente en la identidad, el producto interno en el espacio tangente en un punto arbitrario p se define por

${\displaystyle g_{p}(u,v)=g_{e}(dL_{p^{-1}}(u),dL_{p^{-1}}(v)),}$

donde para un valor arbitrario de x , L _x es la función de multiplicación izquierda G → G que envía un punto y a xy . Las métricas de Riemann construidas de esta manera son invariantes a la izquierda ; las métricas de Riemann invariantes a la derecha también se podrían construir utilizando la función de multiplicación derecha.

La conexión de Levi-Civita y la curvatura de una métrica riemanniana general invariante a la izquierda se pueden calcular explícitamente en términos de g _e , la representación adjunta de G , y el álgebra de Lie asociada a G . ^[36] Estas fórmulas se simplifican considerablemente en el caso especial de una métrica riemanniana que es biinvariante (es decir, simultáneamente invariante a la izquierda y a la derecha). ^[37] Todas las métricas invariantes a la izquierda tienen una curvatura escalar constante.

Las métricas invariantes por la izquierda y bivariantes en grupos de Lie son una fuente importante de ejemplos de variedades de Riemann. Las esferas de Berger , construidas como métricas invariantes por la izquierda en el grupo unitario especial SU(2), se encuentran entre los ejemplos más simples de los fenómenos de colapso , en los que una variedad de Riemann simplemente conexa puede tener un volumen pequeño sin tener una curvatura grande. ^[38] También dan un ejemplo de una métrica de Riemann que tiene una curvatura escalar constante pero que no es Einstein , o incluso de una curvatura de Ricci paralela. ^[39] Al espacio hiperbólico se le puede dar una estructura de grupo de Lie en relación con la cual la métrica es invariante por la izquierda. ^{[40] [41]} Cualquier métrica riemanniana biinvariante en un grupo de Lie tiene una curvatura seccional no negativa, lo que da lugar a una variedad de dichas métricas: a un grupo de Lie se le puede dar una métrica riemanniana biinvariante si y solo si es el producto de un grupo de Lie compacto con un grupo de Lie abeliano . ^[42]

Espacios homogéneos

Se dice que una variedad de Riemann ( M , g ) es homogénea si para cada par de puntos x e y en M , existe alguna isometría f de la variedad de Riemann que envía x a y . Esto se puede reformular en el lenguaje de las acciones de grupo como el requisito de que la acción natural del grupo de isometría sea transitiva. Toda variedad de Riemann homogénea es geodésicamente completa y tiene una curvatura escalar constante. ^[43]

Hasta la isometría, todas las variedades riemannianas homogéneas surgen de la siguiente construcción. Dado un grupo de Lie G con subgrupo compacto K que no contiene ningún subgrupo normal no trivial de G , fije cualquier subespacio complementado W del álgebra de Lie de K dentro del álgebra de Lie de G . Si este subespacio es invariante bajo la función lineal ad _G ( k ): W → W para cualquier elemento k de K , entonces las métricas riemannianas G -invariantes en el espacio de clases laterales G / K están en correspondencia biunívoca con aquellos productos internos en W que son invariantes bajo ad _G ( k ): W → W para cada elemento k de K . ^[44] Cada una de estas métricas riemannianas es homogénea, y G se considera naturalmente como un subgrupo del grupo de isometría completo.

El ejemplo anterior de grupos de Lie con métricas riemannianas invariantes por la izquierda surge como un caso muy especial de esta construcción, es decir, cuando K es el subgrupo trivial que contiene solo el elemento identidad. Los cálculos de la conexión de Levi-Civita y la curvatura a la que se hace referencia allí se pueden generalizar a este contexto, donde ahora los cálculos se formulan en términos del producto interno de W , el álgebra de Lie de G y la descomposición de suma directa del álgebra de Lie de G en el álgebra de Lie de K y W . ^[44] Esto reduce el estudio de la curvatura de variedades riemannianas homogéneas en gran medida a problemas algebraicos. Esta reducción, junto con la flexibilidad de la construcción anterior, hace que la clase de variedades riemannianas homogéneas sea muy útil para construir ejemplos.

Espacios simétricos

Una variedad riemanniana conexa ( M , g ) se dice que es simétrica si para cada punto p de M existe alguna isometría de la variedad con p como punto fijo y para la cual la negación de la diferencial en p es la función identidad . Todo espacio simétrico riemanniano es homogéneo y, en consecuencia, es geodésicamente completo y tiene una curvatura escalar constante. Sin embargo, los espacios simétricos riemannianos también tienen una propiedad de curvatura mucho más fuerte que no poseen la mayoría de las variedades riemannianas homogéneas, a saber, que el tensor de curvatura de Riemann y la curvatura de Ricci son paralelos . Las variedades riemannianas con esta propiedad de curvatura, que podría expresarse libremente como "tensor de curvatura de Riemann constante" (que no debe confundirse con curvatura constante ), se dice que son localmente simétricas . Esta propiedad casi caracteriza a los espacios simétricos; Élie Cartan demostró en la década de 1920 que una variedad de Riemann localmente simétrica que es geodésicamente completa y simplemente conexa debe de hecho ser simétrica. ^[45]

Muchos de los ejemplos fundamentales de variedades de Riemann son simétricos. Los más básicos incluyen la esfera y los espacios proyectivos reales con sus métricas estándar, junto con el espacio hiperbólico. El espacio proyectivo complejo, el espacio proyectivo cuaterniónico y el plano de Cayley son análogos del espacio proyectivo real que también son simétricos, al igual que el espacio hiperbólico complejo , el espacio hiperbólico cuaterniónico y el espacio hiperbólico de Cayley, que en cambio son análogos del espacio hiperbólico. Las variedades de Grassmann también tienen métricas riemannianas naturales que las convierten en espacios simétricos. Entre los grupos de Lie con métricas riemannianas invariantes por la izquierda, aquellos que son biinvariantes son simétricos. ^[45]

Basándose en su formulación algebraica como tipos especiales de espacios homogéneos, Cartan logró una clasificación explícita de los espacios simétricos que son irreducibles , refiriéndose a aquellos que no pueden descomponerse localmente como espacios producto . Cada uno de estos espacios es un ejemplo de una variedad de Einstein ; entre ellos, solo las variedades unidimensionales tienen curvatura escalar cero. Estos espacios son importantes desde la perspectiva de la holonomía de Riemann . Como descubrió en la década de 1950 Marcel Berger , cualquier variedad de Riemann que sea simplemente conexa e irreducible es un espacio simétrico o tiene una holonomía de Riemann que pertenece a una lista de solo siete posibilidades. Seis de las siete excepciones a los espacios simétricos en la clasificación de Berger caen en los campos de la geometría de Kähler , la geometría de cuaterniones-Kähler , la geometría G 2 y la geometría Spin(7) , cada una de las cuales estudia las variedades de Riemann equipadas con ciertas estructuras y simetrías adicionales. La séptima excepción es el estudio de variedades riemannianas "genéricas" sin simetría particular, como lo refleja el grupo de holonomía máxima posible. ^[45]

Variedades de dimensión infinita

Las afirmaciones y teoremas anteriores son para variedades de dimensión finita (variedades cuyos gráficos se asignan a subconjuntos abiertos de ) . Estos pueden extenderse, hasta cierto punto, a variedades de dimensión infinita; es decir, variedades que se modelan a partir de un espacio vectorial topológico ; por ejemplo, las variedades de Fréchet , Banach y Hilbert . ${\displaystyle \mathbb {R} ^{n}.}$

Definiciones

Las métricas de Riemann se definen de manera similar al caso de dimensión finita. Sin embargo, existe una distinción entre dos tipos de métricas de Riemann:

• Una métrica riemanniana débil en es una función suave tal que para cualquier restricción es un producto interno en ^{[ cita requerida ]} ${\displaystyle M}$ ${\displaystyle g:TM\times TM\to \mathbb {R} ,}$ ${\displaystyle x\in M}$ ${\displaystyle g_{x}:T_{x}M\times T_{x}M\to \mathbb {R} }$ ${\displaystyle T_{x}M.}$
• Una métrica riemanniana fuerte en es una métrica riemanniana débil tal que induce la topología en . Si es una métrica riemanniana fuerte, entonces debe ser una variedad de Hilbert. ^{[ cita requerida ]} ${\displaystyle M}$ ${\displaystyle g_{x}}$ ${\displaystyle T_{x}M}$ ${\displaystyle g}$ ${\displaystyle M}$

Ejemplos

• Si es un espacio de Hilbert , entonces para cualquiera se puede identificar con La métrica para todos es una métrica riemanniana fuerte. ^{[ cita requerida ]} ${\displaystyle (H,\langle \,\cdot ,\cdot \,\rangle )}$ ${\displaystyle x\in H,}$ ${\displaystyle H}$ ${\displaystyle T_{x}H.}$ ${\displaystyle g_{x}(u,v)=\langle u,v\rangle }$ ${\displaystyle x,u,v\in H}$
• Sea una variedad compacta de Riemann y denotada por su grupo de difeomorfismo. Este último es una variedad suave ( ver aquí ) y, de hecho, un grupo de Lie . ^{[ cita requerida ]} Su fibrado tangente en la identidad es el conjunto de campos vectoriales suaves en ^{[ cita requerida ]} Sea una forma de volumen en La métrica débil de Riemann en , denotada , se define de la siguiente manera. Sea Entonces para , ${\displaystyle (M,g)}$ ${\displaystyle \operatorname {Diff} (M)}$ ${\displaystyle M.}$ ${\displaystyle \mu }$ ${\displaystyle M.}$ ${\displaystyle L^{2}}$ ${\displaystyle \operatorname {Diff} (M)}$ ${\displaystyle G}$ ${\displaystyle f\in \operatorname {Diff} (M),}$ ${\displaystyle u,v\in T_{f}\operatorname {Diff} (M).}$ ${\displaystyle x\in M,u(x)\in T_{f(x)}M}$

  ${\displaystyle G_{f}(u,v)=\int _{M}g_{f(x)}(u(x),v(x))\,d\mu (x)}$. ^{[ cita requerida ]}

Estructura del espacio métrico

La longitud de las curvas y la función de distancia de Riemann se definen de una manera similar al caso de dimensión finita. La función de distancia , llamada distancia geodésica , es siempre una pseudométrica (una métrica que no separa puntos), pero puede no ser una métrica. ^[46] En el caso de dimensión finita, la prueba de que la función de distancia de Riemann separa puntos utiliza la existencia de un conjunto abierto precompacto alrededor de cualquier punto. En el caso infinito, los conjuntos abiertos ya no son precompactos, por lo que la prueba falla. ${\displaystyle d_{g}:M\times M\to [0,\infty )}$ ${\displaystyle d_{g}}$

• Si es una métrica riemanniana fuerte en , entonces separa puntos (por lo tanto es una métrica) e induce la topología original. ^{[ cita requerida ]} ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle d_{g}}$
• Si es una métrica riemanniana débil, puede fallar en la separación de puntos. De hecho, puede incluso ser idénticamente 0. ^[46] Por ejemplo, si es una variedad riemanniana compacta, entonces la métrica riemanniana débil en induce una distancia geodésica que se desvanece. ^[47] ${\displaystyle g}$ ${\displaystyle d_{g}}$ ${\displaystyle (M,g)}$ ${\displaystyle L^{2}}$ ${\displaystyle \operatorname {Diff} (M)}$

Teorema de Hopf-Rinow

En el caso de métricas riemannianas fuertes, una parte del Hopf-Rinow de dimensión finita todavía se mantiene.

Teorema : Sea una variedad fuerte de Riemann. Entonces, la completitud métrica (en la métrica ) implica completitud geodésica. ^{[ cita requerida ]} ${\displaystyle (M,g)}$ ${\displaystyle d_{g}}$

Sin embargo, una variedad riemanniana fuerte geodésicamente completa podría no ser métricamente completa y podría tener subconjuntos cerrados y acotados que no sean compactos. ^{[ cita requerida ]} Además, una variedad riemanniana fuerte para la cual todos los subconjuntos cerrados y acotados sean compactos podría no ser geodésicamente completa. ^{[ cita requerida ]}

Si es una métrica riemanniana débil, entonces ninguna noción de completitud implica la otra en general. ^{[ cita requerida ]} ${\displaystyle g}$

Véase también

• Colector liso
• Geometría de Riemann
• Colector Finsler
• Variedad subriemanniana
• Variedad pseudo-riemanniana
• Tensor métrico
• Variedad hermítica
• Variedad simpléctica
• Colector de Kahler
• Variedad de Einstein

Referencias

Notas

1. do Carmo 1992, págs. 35-36.
2. do Carmo 1992, pág. 37.
3. do Carmo 1992, pág. 38.
4. Lee 2018, pág. 13.
5. Lee 2018, pág. 26.
6. Lee 2018, pág. 12.
7. Lee 2018, pág. 30.
8. Lee 2018, pág. 31.
9. Lee 2018, págs. 12-13.
10. Lee 2018, pág. 15.
11. Lee 2018, pág. 16.
12. Lee 2018, pág. 20.
13. Lee 2018, pág. 11.
14. Lee 2018, pág. 39.
15. Burtscher 2015, pág. 276.
16. Lee 2018, págs. 89–91.
17. Lee 2018, págs. 122–123.
18. Lee 2018, pág. 100.
19. Lee 2018, págs. 101–102.
20. Lee 2018, pág. 103.
21. Lee 2018, págs. 103–104.
22. Lee 2018, pág. 105.
23. Lee 2018, pág. 156.
24. Lee 2018, pág. 137.
25. Lee 2018, pág. 131.
26. do Carmo 1992, págs. 146-147.
27. Lee 2018, págs. 105–110.
28. Lee 2018, pág. 201.
29. Lee 2018, pág. 200.
30. Lee 2018, págs. 196–197.
31. Lee 2018, pág. 207.
32. Lee 2018, pág. 210.
33. Wolf 2011, Capítulo 2.
34. Wolf 2011, Capítulos 2 y 7.
35. Wolf 2011, Capítulos 2 y 3.
36. Cheeger y Ebin 2008, Proposición 3.18.
37. Cheeger y Ebin 2008, Corolario 3.19; Petersen 2016, Sección 4.4.
38. Petersen 2016, Sección 4.4.3 y pág. 399.
39. Petersen 2016, pág. 369.
40. En el modelo de semiespacio superior del espacio hiperbólico, la estructura del grupo de Lie se define por ${\displaystyle (x_{1},\ldots ,x_{n})\cdot (y_{1},\ldots ,y_{n})=(x_{1}+y_{n}x_{1},\ldots ,x_{n-1}+y_{n}x_{n-1},x_{n}y_{n}).}$
41. Lee 2018, Ejemplo 3.16f.
42. Lee 2018, pág. 72; Milnor 1976.
43. Kobayashi y Nomizu 1963, Teorema IV.4.5.
44. Besse 1987, Sección 7C.
45. Petersen 2016, Capítulo 10.
46. Magnani y Tiberio 2020.
47. Michor y Mumford 2005.

Fuentes

• Besse, Arthur L. (1987). Variedades de Einstein . Ergebnisse der Mathematik und ihrer Grenzgebiete (3). vol. 10. Berlín: Springer-Verlag . doi :10.1007/978-3-540-74311-8. ISBN 3-540-15279-2. Sr.  0867684. Zbl  0613.53001.
• Cheeger, Jeff ; Ebin, David G. (2008). Teoremas de comparación en geometría de Riemann (reimpresión revisada de la edición original de 1975). Providence, RI: AMS Chelsea Publishing . doi :10.1090/chel/365. ISBN 978-0-8218-4417-5.MR  2394158.Zbl 1142.53003  .​
• do Carmo, Manfredo Perdigão (1992). Geometría de Riemann . Matemáticas: teoría y aplicaciones (traducido de la segunda edición portuguesa de la edición original de 1979). Boston, MA: Birkhäuser Boston . ISBN 978-0-8176-3490-2.MR  1138207.Zbl 0752.53001  .​
• Gromov, Misha (1999). Estructuras métricas para espacios riemannianos y no riemannianos . Progress in Mathematics. Vol. 152. Traducido por Bates, Sean Michael. Con apéndices de M. Katz , P. Pansu y S. Semmes . (Basado en la edición original en francés de 1981). Boston, MA: Birkhäuser Boston, Inc. doi :10.1007/978-0-8176-4583-0. ISBN . 0-8176-3898-9.MR  1699320.Zbl 0953.53002  .​
• Kobayashi, Shoshichi ; Nomizu, Katsumi (1963). Fundamentos de geometría diferencial. Volumen I . Nueva York–Londres: John Wiley & Sons, Inc. MR  0152974. Zbl  0119.37502.
• Lee, John M. (2018). Introducción a las variedades de Riemann . Springer-Verlag . ISBN 978-3-319-91754-2.
• Petersen, Peter (2016). Geometría de Riemann . Textos de posgrado en matemáticas . Vol. 171 (tercera edición de la edición original de 1998). Springer, Cham . doi :10.1007/978-3-319-26654-1. ISBN . 978-3-319-26652-7.MR 3469435.Zbl 1417.53001  . ​
• Wolf, Joseph A. (2011). Espacios de curvatura constante (sexta edición de la edición original de 1967). Providence, RI: AMS Chelsea Publishing . doi :10.1090/chel/372. ISBN. 978-0-8218-5282-8.MR  2742530.Zbl 1216.53003  .​
• Burtscher, Annegret (2015). "Estructuras de longitud en variedades con métricas riemannianas continuas". New York Journal of Mathematics . 21 : 273–296. ISSN  1076-9803.
• Magnani, Valentino; Tiberio, Daniele (2020). "Una observación sobre la desaparición de las distancias geodésicas en dimensiones infinitas". Proc. Amer. Math. Soc . 148 (1): 3653–3656. arXiv : 1910.06430 . doi :10.1090/proc/14986. S2CID  204578276.
• Michor, Peter W.; Mumford, David (2005). "Desvanecimiento de la distancia geodésica en espacios de subvariedades y difeomorfismos". Documenta Math . 10 : 217–245. arXiv : math/0409303 . doi :10.4171/dm/187. S2CID  69260.
• Milnor, John (1976). "Curvaturas de métricas invariantes por la izquierda en grupos de Lie". Avances en Matemáticas . 21 (3): 293–329. doi : 10.1016/S0001-8708(76)80002-3 . MR  0425012. Zbl  0341.53030.

Enlaces externos

• LA Sidorov (2001) [1994], "Métrica de Riemann", Enciclopedia de Matemáticas , EMS Press