
La geometría algebraica es una rama de las matemáticas que utiliza técnicas algebraicas abstractas , principalmente del álgebra conmutativa , para resolver problemas geométricos . Clásicamente estudia ceros de polinomios multivariados ; el enfoque moderno generaliza esto en algunos aspectos diferentes.
Los objetos fundamentales de estudio en geometría algebraica son las variedades algebraicas , que son manifestaciones geométricas de soluciones de sistemas de ecuaciones polinómicas . Ejemplos de las clases de variedades algebraicas más estudiadas son líneas , círculos , parábolas , elipses , hipérbolas , curvas cúbicas como las elípticas y curvas cuárticas como las lemniscatas y los óvalos de Cassini . Estas son curvas algebraicas planas . Un punto del plano se encuentra en una curva algebraica si sus coordenadas satisfacen una ecuación polinómica dada . Las preguntas básicas implican el estudio de puntos de especial interés como puntos singulares , puntos de inflexión y puntos en el infinito . Las preguntas más avanzadas involucran la topología de la curva y la relación entre curvas definidas por diferentes ecuaciones.
La geometría algebraica ocupa un lugar central en las matemáticas modernas y tiene múltiples conexiones conceptuales con campos tan diversos como el análisis complejo , la topología y la teoría de números . Como estudio de sistemas de ecuaciones polinomiales en varias variables, el tema de la geometría algebraica comienza con la búsqueda de soluciones específicas mediante la resolución de ecuaciones , y luego procede a comprender las propiedades intrínsecas de la totalidad de soluciones de un sistema de ecuaciones. Esta comprensión requiere tanto de teoría conceptual como de técnica computacional.
En el siglo XX, la geometría algebraica se dividió en varias subáreas.
Gran parte del desarrollo de la corriente principal de la geometría algebraica en el siglo XX se produjo dentro de un marco algebraico abstracto, con un énfasis cada vez mayor en las propiedades "intrínsecas" de las variedades algebraicas que no dependen de ninguna forma particular de incrustar la variedad en un espacio de coordenadas ambiental; esto es paralelo a los desarrollos en topología, geometría diferencial y compleja . Un logro clave de esta geometría algebraica abstracta es la teoría de esquemas de Grothendieck , que permite utilizar la teoría de gavillas para estudiar variedades algebraicas de una manera muy similar a su uso en el estudio de variedades diferenciales y analíticas . Esto se obtiene ampliando la noción de punto: en geometría algebraica clásica, un punto de una variedad afín puede identificarse, a través del Nullstellensatz de Hilbert , con un ideal máximo del anillo de coordenadas , mientras que los puntos del esquema afín correspondiente son todos ideales primos. de este anillo. Esto significa que un punto de dicho esquema puede ser un punto habitual o una subvariedad. Este enfoque también permite una unificación del lenguaje y las herramientas de la geometría algebraica clásica, principalmente relacionada con puntos complejos, y de la teoría algebraica de números. La prueba de Wiles de la antigua conjetura llamada último teorema de Fermat es un ejemplo del poder de este enfoque.
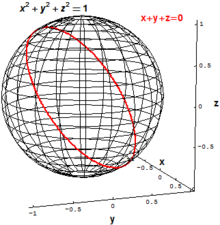
En geometría algebraica clásica, los principales objetos de interés son los conjuntos de colecciones de polinomios que se desvanecen , es decir, el conjunto de todos los puntos que satisfacen simultáneamente una o más ecuaciones polinómicas . Por ejemplo, la esfera bidimensional de radio 1 en el espacio euclidiano tridimensional R 3 podría definirse como el conjunto de todos los puntos ( x , y , z ) con
Un círculo "inclinado" en R 3 se puede definir como el conjunto de todos los puntos ( x , y , z ) que satisfacen las dos ecuaciones polinómicas.
Primero comenzamos con un campo k . En la geometría algebraica clásica, este campo siempre fueron los números complejos C , pero muchos de los mismos resultados son ciertos si asumimos únicamente que k es algebraicamente cerrado . Consideramos el espacio afín de dimensión n sobre k , denotado An ( k ) (o más simplemente An , cuando k queda claro por el contexto) . Cuando se fija un sistema de coordenadas, se puede identificar A n ( k ) con k n . El propósito de no trabajar con k n es enfatizar que uno "olvida" la estructura del espacio vectorial que lleva k n .
Una función f : A n → A 1 se dice polinomio (o regular ) si se puede escribir como polinomio, es decir, si existe un polinomio p en k [ x 1 ,..., x n ] tal que f ( M ) = p ( t 1 ,..., t n ) para cada punto M con coordenadas ( t 1 ,..., t n ) en A n . La propiedad de una función de ser polinómica (o regular) no depende de la elección de un sistema de coordenadas en An .
Cuando se elige un sistema de coordenadas, las funciones regulares en el espacio n afín pueden identificarse con el anillo de funciones polinómicas en n variables sobre k . Por lo tanto, el conjunto de funciones regulares en An es un anillo, que se denota k [ An ] .
Decimos que un polinomio desaparece en un punto si al evaluarlo en ese punto se obtiene cero. Sea S un conjunto de polinomios en k [ A n ]. El conjunto evanescente de S (o lugar geométrico evanescente o conjunto cero ) es el conjunto V ( S ) de todos los puntos en An donde todo polinomio en S desaparece. Simbólicamente,
Un subconjunto de An que es V ( S ), para algún S , se llama conjunto algebraico . La V significa variedad (un tipo específico de conjunto algebraico que se definirá más adelante).
Dado un subconjunto U de An , ¿se puede recuperar el conjunto de polinomios que lo generan ? Si U es cualquier subconjunto de An , defina I ( U ) como el conjunto de todos los polinomios cuyo conjunto evanescente contiene U. I significa ideal : si dos polinomios f y g desaparecen en U , entonces f + g desaparece en U , y si h es cualquier polinomio, entonces hf desaparece en U , por lo que I ( U ) es siempre un ideal del polinomio anillo k [ Una norte ].
Dos preguntas naturales que hacer son:
La respuesta a la primera pregunta se proporciona introduciendo la topología de Zariski , una topología sobre An cuyos conjuntos cerrados son los conjuntos algebraicos, y que refleja directamente la estructura algebraica de k [ An ] . Entonces U = V ( I ( U )) si y sólo si U es un conjunto algebraico o equivalentemente un conjunto cerrado de Zariski. La respuesta a la segunda pregunta la da el Nullstellensatz de Hilbert . En una de sus formas, dice que I ( V ( S )) es el radical del ideal generado por S. En un lenguaje más abstracto, existe una conexión de Galois , que da lugar a dos operadores de cierre ; pueden identificarse y, naturalmente, desempeñan un papel básico en la teoría; el ejemplo se elabora en la conexión de Galois.
Por diversas razones es posible que no siempre queramos trabajar con el ideal completo correspondiente a un conjunto algebraico U. El teorema de la base de Hilbert implica que los ideales en k [ An ] siempre se generan de forma finita.
Un conjunto algebraico se dice irreducible si no puede escribirse como la unión de dos conjuntos algebraicos más pequeños. Cualquier conjunto algebraico es una unión finita de conjuntos algebraicos irreducibles y esta descomposición es única. Por tanto, sus elementos se denominan componentes irreducibles del conjunto algebraico. A un conjunto algebraico irreducible también se le llama variedad . Resulta que un conjunto algebraico es una variedad si y sólo si puede definirse como el conjunto evanescente de un ideal primo del anillo polinómico.
Algunos autores no hacen una distinción clara entre conjuntos algebraicos y variedades y utilizan variedades irreducibles para hacer la distinción cuando es necesario.
Así como las funciones continuas son las funciones naturales en espacios topológicos y las funciones suaves son las funciones naturales en variedades diferenciables , existe una clase natural de funciones en un conjunto algebraico, llamadas funciones regulares o funciones polinómicas . Una función regular en un conjunto algebraico V contenido en An es la restricción a V de una función regular en An . Para un conjunto algebraico definido en el campo de los números complejos, las funciones regulares son fluidas e incluso analíticas .
Puede parecer anormalmente restrictivo exigir que una función regular siempre se extienda hasta el espacio ambiental, pero es muy similar a la situación en un espacio topológico normal , donde el teorema de extensión de Tietze garantiza que una función continua en un subconjunto cerrado siempre se extiende hasta el espacio topológico ambiental.
Al igual que con las funciones regulares en el espacio afín, las funciones regulares en V forman un anillo, que denotamos por k [ V ]. Este anillo se llama anillo de coordenadas de V.
Dado que las funciones regulares en V provienen de funciones regulares en An , existe una relación entre los anillos de coordenadas . Específicamente, si una función regular en V es la restricción de dos funciones f y g en k [ A n ], entonces f − g es una función polinómica que es nula en V y por tanto pertenece a I ( V ). Por tanto, k [ V ] puede identificarse con k [ An ]/ I ( V ).
Usando funciones regulares de una variedad afín a A 1 , podemos definir mapas regulares de una variedad afín a otra. Primero definiremos una aplicación regular de una variedad en un espacio afín: Sea V una variedad contenida en An . Elija m funciones regulares en V y llámelas f 1 , ..., f m . Definimos un mapa regular f de V a Am dejando f = ( f 1 , ..., f m ) . En otras palabras, cada f i determina una coordenada del rango de f .
Si V ′ es una variedad contenida en A m , decimos que f es una aplicación regular de V a V ′ si el rango de f está contenido en V ′.
La definición de aplicaciones regulares se aplica también a conjuntos algebraicos. Los mapas regulares también se llaman morfismos , ya que agrupan la colección de todos los conjuntos algebraicos afines en una categoría , donde los objetos son los conjuntos algebraicos afines y los morfismos son los mapas regulares. Las variedades afines son una subcategoría de la categoría de conjuntos algebraicos.
Dado un mapa regular g de V a V ′ y una función regular f de k [ V ′], entonces f ∘ g ∈ k [ V ] . El mapa f → f ∘ g es un homomorfismo de anillo de k [ V ′] a k [ V ]. Por el contrario, cada homomorfismo de anillo de k [ V ′] a k [ V ] define un mapa regular de V a V ′. Esto define una equivalencia de categorías entre la categoría de conjuntos algebraicos y la categoría opuesta de las k -álgebras reducidas generadas finitamente . Esta equivalencia es uno de los puntos de partida de la teoría de esquemas .
A diferencia de las secciones anteriores, esta sección se refiere sólo a variedades y no a conjuntos algebraicos. Por otro lado, las definiciones se extienden naturalmente a las variedades proyectivas (sección siguiente), ya que una variedad afín y su compleción proyectiva tienen el mismo campo de funciones.
Si V es una variedad afín, su anillo de coordenadas es un dominio integral y, por lo tanto, tiene un campo de fracciones que se denota k ( V ) y se llama campo de las funciones racionales en V o, en breve, campo de función de V. Sus elementos son las restricciones a V de las funciones racionales sobre el espacio afín que contiene V. El dominio de una función racional f no es V sino el complemento de la subvariedad (una hipersuperficie) donde el denominador de f desaparece.
Como ocurre con las aplicaciones regulares, se puede definir una aplicación racional desde una variedad V hasta una variedad V '. Al igual que con los mapas regulares, los mapas racionales de V a V ' pueden identificarse con los homomorfismos de campo de k ( V ' ) a k ( V ).
Dos variedades afines son biracionalmente equivalentes si hay dos funciones racionales entre ellas que son inversas entre sí en las regiones donde ambas están definidas. De manera equivalente, son biracionalmente equivalentes si sus campos funcionales son isomórficos.
Una variedad afín es una variedad racional si es biracionalmente equivalente a un espacio afín. Esto significa que la variedad admite una parametrización racional , es decir una parametrización con funciones racionales . Por ejemplo, el círculo de la ecuación es una curva racional, ya que tiene la ecuación paramétrica
que también puede verse como un mapa racional de la línea al círculo.
El problema de resolución de singularidades es saber si toda variedad algebraica es biracionalmente equivalente a una variedad cuya terminación proyectiva es no singular (ver también terminación suave ). Fue resuelto afirmativamente en la característica 0 por Heisuke Hironaka en 1964 y aún no está resuelto en la característica finita.

Así como las fórmulas para las raíces de polinomios de segundo, tercer y cuarto grado sugieren extender los números reales al escenario más algebraicamente completo de los números complejos, muchas propiedades de las variedades algebraicas sugieren extender el espacio afín a un espacio proyectivo geométricamente más completo. Mientras que los números complejos se obtienen sumando el número i , una raíz del polinomio x 2 + 1 , el espacio proyectivo se obtiene sumando puntos apropiados "en el infinito", puntos donde pueden encontrarse líneas paralelas.
Para ver cómo podría ocurrir esto, considere la variedad V ( y − x 2 ) . Si lo dibujamos, obtenemos una parábola . A medida que x tiende a infinito positivo, la pendiente de la recta desde el origen hasta el punto ( x , x 2 ) también tiende a infinito positivo. Cuando x tiende a infinito negativo, la pendiente de la misma recta tiende a infinito negativo.
Compare esto con la variedad V ( y − x 3 ). Esta es una curva cúbica . Cuando x tiende a infinito positivo, la pendiente de la recta desde el origen hasta el punto ( x , x 3 ) tiende a infinito positivo tal como antes. Pero a diferencia de antes, cuando x llega al infinito negativo, la pendiente de la misma recta también llega al infinito positivo; exactamente lo contrario de la parábola. Entonces el comportamiento "en el infinito" de V ( y − x 3 ) es diferente del comportamiento "en el infinito" de V ( y − x 2 ).
La consideración de la terminación proyectiva de las dos curvas, que es su prolongación "al infinito" en el plano proyectivo , permite cuantificar esta diferencia: el punto al infinito de la parábola es un punto regular , cuya tangente es la recta al infinito. , mientras que el punto en el infinito de la curva cúbica es una cúspide . Además, ambas curvas son racionales, ya que están parametrizadas por x , y el teorema de Riemann-Roch implica que la curva cúbica debe tener una singularidad, que debe estar en el infinito, ya que todos sus puntos en el espacio afín son regulares.
Por tanto, muchas de las propiedades de las variedades algebraicas, incluida la equivalencia biracional y todas las propiedades topológicas, dependen del comportamiento "en el infinito", por lo que es natural estudiar las variedades en el espacio proyectivo. Además, la introducción de técnicas proyectivas hizo que muchos teoremas de geometría algebraica fueran más simples y nítidos: por ejemplo, el teorema de Bézout sobre el número de puntos de intersección entre dos variedades puede expresarse en su forma más nítida sólo en el espacio proyectivo. Por estas razones, el espacio proyectivo juega un papel fundamental en la geometría algebraica.
Hoy en día, el espacio proyectivo P n de dimensión n suele definirse como el conjunto de las rectas que pasan por un punto, considerado como origen, en el espacio afín de dimensión n + 1 , o equivalentemente al conjunto de las rectas vectoriales en un espacio vectorial de dimensión n + 1 . Cuando se ha elegido un sistema de coordenadas en el espacio de dimensión n + 1 , todos los puntos de una recta tienen el mismo conjunto de coordenadas, hasta la multiplicación por un elemento de k . Esto define las coordenadas homogéneas de un punto de P n como una secuencia de n + 1 elementos del campo base k , definida hasta la multiplicación por un elemento distinto de cero de k (lo mismo para toda la secuencia).
Un polinomio en n + 1 variables se anula en todos los puntos de una recta que pasa por el origen si y sólo si es homogénea . En este caso, se dice que el polinomio desaparece en el punto correspondiente de P n . Esto nos permite definir un conjunto algebraico proyectivo en P n como el conjunto V ( f 1 , ..., f k ) , donde un conjunto finito de polinomios homogéneos { f 1 , ..., f k } desaparece. Como ocurre con los conjuntos algebraicos afines, existe una biyección entre los conjuntos algebraicos proyectivos y los ideales homogéneos reducidos que los definen. Las variedades proyectivas son los conjuntos algebraicos proyectivos cuyo ideal definitorio es primo. En otras palabras, una variedad proyectiva es un conjunto algebraico proyectivo, cuyo anillo de coordenadas homogéneo es un dominio integral , definiéndose el anillo de coordenadas proyectivas como el cociente del anillo graduado o de los polinomios en n + 1 variables por el ideal homogéneo (reducido) definiendo la variedad. Todo conjunto algebraico proyectivo puede descomponerse de forma única en una unión finita de variedades proyectivas.
Las únicas funciones regulares que pueden definirse adecuadamente en una variedad proyectiva son las funciones constantes. Por tanto, esta noción no se utiliza en situaciones proyectivas. Por otro lado, es una noción útil el campo de las funciones racionales o campo de funciones , que, al igual que el caso afín, se define como el conjunto de los cocientes de dos elementos homogéneos del mismo grado en el anillo de coordenadas homogéneo.
La geometría algebraica real es el estudio de variedades algebraicas reales.
En un estudio de este tipo no se puede ignorar el hecho de que el campo de los números reales es un campo ordenado . Por ejemplo, la curva de la ecuación es un círculo si , pero no tiene puntos reales si . La geometría algebraica real también investiga, de manera más amplia, los conjuntos semialgebraicos , que son las soluciones de sistemas de desigualdades polinómicas. Por ejemplo, ninguna de las ramas de la hipérbola de la ecuación es una variedad algebraica real. Sin embargo, la rama del primer cuadrante es un conjunto semialgebraico definido por y .
Un problema abierto en geometría algebraica real es la siguiente parte del decimosexto problema de Hilbert : decidir qué posiciones respectivas son posibles para los óvalos de una curva plana no singular de grado 8.
Se puede fechar el origen de la geometría algebraica computacional en la reunión EUROSAM'79 (Simposio Internacional sobre Manipulación Simbólica y Algebraica) celebrada en Marsella , Francia, en junio de 1979. En esta reunión,
Desde entonces, la mayoría de los resultados en esta área están relacionados con uno o varios de estos ítems, ya sea utilizando o mejorando uno de estos algoritmos, o encontrando algoritmos cuya complejidad sea simplemente exponencial en el número de variables.
En las últimas décadas se ha desarrollado un cuerpo de teoría matemática complementario a los métodos simbólicos llamado geometría algebraica numérica . El principal método computacional es la continuación de homotopía . Esto soporta, por ejemplo, un modelo de cálculo de coma flotante para resolver problemas de geometría algebraica.
Una base de Gröbner es un sistema de generadores de un polinomio ideal cuyo cálculo permite deducir muchas propiedades de la variedad algebraica afín definida por el ideal.
Dado un ideal I definiendo un conjunto algebraico V :
Los cálculos de la base de Gröbner no permiten calcular directamente la descomposición primaria de I ni los ideales primos que definen los componentes irreducibles de V , pero la mayoría de los algoritmos para esto implican el cálculo de la base de Gröbner. Los algoritmos que no se basan en bases de Gröbner utilizan cadenas regulares pero pueden necesitar bases de Gröbner en algunas situaciones excepcionales.
Se considera que las bases de Gröbner son difíciles de calcular. De hecho pueden contener, en el peor de los casos, polinomios cuyo grado es doblemente exponencial en el número de variables y un número de polinomios que también es doblemente exponencial. Sin embargo, esto es sólo el peor de los casos de complejidad, y el límite de complejidad del algoritmo de Lazard de 1979 puede aplicarse con frecuencia. El algoritmo Faugère F5 se da cuenta de esta complejidad, ya que puede verse como una mejora del algoritmo de Lazard de 1979. De ello se deduce que las mejores implementaciones permiten calcular casi de forma rutinaria con conjuntos algebraicos de grado superior a 100. Esto significa que, actualmente, la dificultad de calcular una base de Gröbner está fuertemente relacionada con la dificultad intrínseca del problema.
CAD es un algoritmo introducido en 1973 por G. Collins para implementar con una complejidad aceptable el teorema de Tarski-Seidenberg sobre la eliminación de cuantificadores de los números reales.
Este teorema se refiere a las fórmulas de la lógica de primer orden cuyas fórmulas atómicas son igualdades polinómicas o desigualdades entre polinomios con coeficientes reales. Estas fórmulas son, por tanto, las fórmulas que pueden construirse a partir de fórmulas atómicas mediante los operadores lógicos y (∧), o (∨), no (¬), para todo (∀) y existe (∃). El teorema de Tarski afirma que, a partir de dicha fórmula, se puede calcular una fórmula equivalente sin cuantificador (∀, ∃).
La complejidad del CAD es doblemente exponencial en el número de variables. Esto significa que CAD permite, en teoría, resolver todos los problemas de geometría algebraica real que puedan expresarse mediante dicha fórmula, es decir, casi todos los problemas relacionados con variedades y conjuntos semialgebraicos dados explícitamente.
Mientras que el cálculo de la base de Gröbner tiene una complejidad doblemente exponencial sólo en casos excepcionales, el CAD casi siempre tiene esta alta complejidad. Esto implica que, a menos que la mayoría de los polinomios que aparecen en la entrada sean lineales, es posible que no resuelva problemas con más de cuatro variables.
Desde 1973, la mayor parte de la investigación sobre este tema se dedica a mejorar el CAD o a encontrar algoritmos alternativos en casos especiales de interés general.
Como ejemplo del estado del arte, existen algoritmos eficientes para encontrar al menos un punto en cada componente conexo de un conjunto semialgebraico y así probar si un conjunto semialgebraico está vacío. Por otro lado, CAD sigue siendo, en la práctica, el mejor algoritmo para contar el número de componentes conectados.
Los algoritmos generales básicos de la geometría computacional tienen una complejidad exponencial doble en el peor de los casos . Más precisamente, si d es el grado máximo de los polinomios de entrada y n el número de variables, su complejidad es como máximo para alguna constante c y, para algunas entradas, la complejidad es al menos para otra constante c ′.
Durante los últimos 20 años del siglo XX se han introducido diversos algoritmos para resolver subproblemas específicos con mayor complejidad. La mayoría de estos algoritmos tienen cierta complejidad . [1]
Entre estos algoritmos que resuelven un subproblema de los problemas resueltos por bases de Gröbner, se pueden citar probar si una variedad afín está vacía y resolver sistemas polinomiales no homogéneos que tienen un número finito de soluciones. Estos algoritmos rara vez se implementan porque, en la mayoría de las entradas, los algoritmos F4 y F5 de Faugère tienen una mejor eficiencia práctica y probablemente una complejidad similar o mejor ( probablemente porque la evaluación de la complejidad de los algoritmos basados en Gröbner en una clase particular de entradas es una tarea difícil que se ha hecho sólo en unos pocos casos especiales).
Los principales algoritmos de geometría algebraica real que resuelven un problema resuelto mediante CAD están relacionados con la topología de conjuntos semialgebraicos. Se puede citar contar el número de componentes conectados , probar si dos puntos están en los mismos componentes o calcular una estratificación de Whitney de un conjunto algebraico real . Tienen una complejidad de , pero la constante involucrada en la notación O es tan alta que usarlos para resolver cualquier problema no trivial efectivamente resuelto por CAD es imposible, incluso si se pudiera usar toda la potencia informática existente en el mundo. Por lo tanto, estos algoritmos nunca se han implementado y esta es un área de investigación activa para buscar algoritmos que tengan en conjunto una buena complejidad asintótica y una buena eficiencia práctica.
Los enfoques modernos de la geometría algebraica redefinen y amplían efectivamente la gama de objetos básicos en varios niveles de generalidad a esquemas, esquemas formales , esquemas ind , espacios algebraicos , pilas algebraicas , etc. La necesidad de esto surge ya de las ideas útiles dentro de la teoría de variedades, por ejemplo, las funciones formales de Zariski pueden acomodarse introduciendo elementos nilpotentes en los anillos estructurales; considerar espacios de bucles y arcos, construir cocientes mediante acciones grupales y desarrollar fundamentos formales para la teoría de la intersección natural y la teoría de la deformación conducen a algunas de las extensiones adicionales.
Lo más notable es que, a finales de la década de 1950, las variedades algebraicas fueron incluidas en el concepto de esquema de Alexander Grothendieck . Sus objetos locales son esquemas afines o espectros primos que son espacios localmente anillados que forman una categoría que es antiequivalente a la categoría de anillos unitales conmutativos, extendiendo la dualidad entre la categoría de variedades algebraicas afines sobre un campo k , y la categoría de finitamente generada. k -álgebras reducidas . El pegado se realiza según la topología de Zariski; uno puede pegar dentro de la categoría de espacios localmente anillados, pero también, usando la incrustación de Yoneda, dentro de la categoría más abstracta de prehaces de conjuntos sobre la categoría de esquemas afines. La topología de Zariski en el sentido de la teoría de conjuntos se reemplaza entonces por una topología de Grothendieck . Grothendieck introdujo las topologías de Grothendieck teniendo en mente ejemplos más exóticos pero geométricamente más finos y más sensibles que la cruda topología de Zariski, a saber, la topología étale , y las dos topologías planas de Grothendieck: fppf y fpqc; hoy en día algunos otros ejemplos se hicieron prominentes, incluida la topología de Nisnevich . Además, las gavillas se pueden generalizar a pilas en el sentido de Grothendieck, generalmente con algunas condiciones de representabilidad adicionales que conducen a pilas de Artin y, aún más finamente, pilas de Deligne-Mumford , ambas a menudo llamadas pilas algebraicas.
A veces, otros sitios algebraicos reemplazan la categoría de esquemas afines. Por ejemplo, Nikolai Durov ha introducido las mónadas algebraicas conmutativas como una generalización de objetos locales en una geometría algebraica generalizada. En esta configuración se realizaron versiones de una geometría tropical , de una geometría absoluta sobre un campo de un elemento y un análogo algebraico de la geometría de Arakelov .
Es posible otra generalización formal de la geometría algebraica universal en la que cada variedad de álgebras tiene su propia geometría algebraica. El término variedad de álgebras no debe confundirse con variedad algebraica .
El lenguaje de esquemas, pilas y generalizaciones ha demostrado ser una forma valiosa de abordar conceptos geométricos y se convirtió en piedras angulares de la geometría algebraica moderna.
Las pilas algebraicas se pueden generalizar aún más y, para muchas cuestiones prácticas, como la teoría de la deformación y la teoría de la intersección, este suele ser el enfoque más natural. Se puede extender el sitio de Grothendieck de esquemas afines a un sitio categórico superior de esquemas afines derivados , reemplazando los anillos conmutativos con una categoría infinita de álgebras conmutativas graduadas diferenciales , o de anillos conmutativos simpliciales o una categoría similar con una variante apropiada de Grothendieck. topología. También se pueden reemplazar prehaces de conjuntos por prehaces de conjuntos simpliciales (o de grupoides infinitos). Entonces, en presencia de una maquinaria homotópica apropiada, se puede desarrollar una noción de pila derivada como tal prehaz en la categoría infinita de esquemas afines derivados, que satisface cierta versión categórica infinita de un axioma de gavilla (y para ser algebraico, inductivamente una secuencia de condiciones de representabilidad). Las categorías del modelo de Quillen , las categorías de Segal y las cuasicategorías son algunas de las herramientas más utilizadas para formalizar esto y producir la geometría algebraica derivada , introducida por la escuela de Carlos Simpson , incluidos Andre Hirschowitz, Bertrand Toën , Gabrielle Vezzosi, Michel Vaquié y otros; y desarrollado aún más por Jacob Lurie , Bertrand Toën y Gabriele Vezzosi . Maxim Kontsevich y sus seguidores desarrollaron desde principios de la década de 1990 otra versión (no conmutativa) de la geometría algebraica derivada, que utiliza categorías A-infinito .
Algunas de las raíces de la geometría algebraica se remontan al trabajo de los griegos helenísticos del siglo V a.C. El problema de Delian , por ejemplo, consistía en construir una longitud x de modo que el cubo de lado x contuviera el mismo volumen que la caja rectangular a 2 b para lados a y b dados . Menecmo ( c. 350 aC ) consideró el problema geométricamente intersectando el par de cónicas planas ay = x 2 y xy = ab . [2] En el siglo III a. C., Arquímedes y Apolonio estudiaron sistemáticamente problemas adicionales sobre secciones cónicas utilizando coordenadas. [2] [3] Apolonio en las Cónicas desarrolló aún más un método que es tan similar a la geometría analítica que a veces se piensa que su trabajo se anticipó al trabajo de Descartes en unos 1800 años. [4] Su aplicación de líneas de referencia, un diámetro y una tangente no es esencialmente diferente de nuestro uso moderno de un sistema de coordenadas, donde las distancias medidas a lo largo del diámetro desde el punto de tangencia son las abscisas y los segmentos paralelos a la tangente. e interceptadas entre el eje y la curva están las ordenadas. Además, desarrolló las relaciones entre las abscisas y las coordenadas correspondientes utilizando métodos geométricos como parábolas y curvas. [5] [6] [7] Los matemáticos medievales, incluidos Omar Khayyam , Leonardo de Pisa , Gersonides y Nicole Oresme en el período medieval , [8] resolvieron ciertas ecuaciones cúbicas y cuadráticas por medios puramente algebraicos y luego interpretaron los resultados geométricamente. El matemático persa Omar Khayyám (nacido en 1048 d.C.) creía que existía una relación entre la aritmética , el álgebra y la geometría . [9] [10] [11] Esto fue criticado por Jeffrey Oaks, quien afirma que el estudio de curvas mediante ecuaciones se originó con Descartes en el siglo XVII. [12]
Estas técnicas de aplicación de construcciones geométricas a problemas algebraicos también fueron adoptadas por varios matemáticos del Renacimiento como Gerolamo Cardano y Niccolò Fontana "Tartaglia" en sus estudios de la ecuación cúbica. El enfoque geométrico de los problemas de construcción, en lugar del algebraico, fue favorecido por la mayoría de los matemáticos de los siglos XVI y XVII, en particular Blaise Pascal , quien se opuso al uso de métodos algebraicos y analíticos en geometría. [13] Los matemáticos franceses Franciscus Vieta y más tarde René Descartes y Pierre de Fermat revolucionaron la forma convencional de pensar en los problemas de construcción mediante la introducción de la geometría de coordenadas . Estaban interesados principalmente en las propiedades de las curvas algebraicas , como las definidas por las ecuaciones diofánticas (en el caso de Fermat), y en la reformulación algebraica de las obras griegas clásicas sobre cónicas y cúbicas (en el caso de Descartes).
Durante el mismo período, Blaise Pascal y Gérard Desargues abordaron la geometría desde una perspectiva diferente, desarrollando las nociones sintéticas de geometría proyectiva . Pascal y Desargues también estudiaron las curvas, pero desde el punto de vista puramente geométrico: el análogo de la construcción griega con regla y compás . Al final, ganó la geometría analítica de Descartes y Fermat, ya que proporcionó a los matemáticos del siglo XVIII herramientas cuantitativas concretas necesarias para estudiar problemas físicos utilizando el nuevo cálculo de Newton y Leibniz . Sin embargo, a finales del siglo XVIII, la mayor parte del carácter algebraico de la geometría de coordenadas quedó subsumido por el cálculo de infinitesimales de Lagrange y Euler .
Fueron necesarios los desarrollos simultáneos del siglo XIX de la geometría no euclidiana y las integrales abelianas para devolver las viejas ideas algebraicas al pliegue geométrico. El primero de estos nuevos desarrollos fue adoptado por Edmond Laguerre y Arthur Cayley , quienes intentaron determinar las propiedades métricas generalizadas del espacio proyectivo. Cayley introdujo la idea de formas polinómicas homogéneas , y más específicamente formas cuadráticas , en el espacio proyectivo. Posteriormente, Felix Klein estudió la geometría proyectiva (junto con otros tipos de geometría) desde el punto de vista de que la geometría en un espacio está codificada en una determinada clase de transformaciones en el espacio. A finales del siglo XIX, los geómetras proyectivos estudiaban tipos más generales de transformaciones de figuras en el espacio proyectivo. En lugar de las transformaciones lineales proyectivas que normalmente se consideraban que daban la geometría kleiniana fundamental en el espacio proyectivo, se preocuparon también por las transformaciones biracionales de mayor grado . Esta noción más débil de congruencia llevaría más tarde a los miembros de la escuela italiana de geometría algebraica del siglo XX a clasificar superficies algebraicas hasta el isomorfismo biracional .
El segundo desarrollo de principios del siglo XIX, el de las integrales abelianas, llevaría a Bernhard Riemann al desarrollo de las superficies de Riemann .
En el mismo período se inició la algebraización de la geometría algebraica mediante el álgebra conmutativa . Los resultados destacados en esta dirección son el teorema de base de Hilbert y el Nullstellensatz de Hilbert , que son la base de la conexión entre la geometría algebraica y el álgebra conmutativa, y la resultante multivariada de Macaulay , que es la base de la teoría de la eliminación . Probablemente debido al tamaño del cálculo que implican las resultantes multivariadas, la teoría de la eliminación fue olvidada a mediados del siglo XX hasta que fue renovada por la teoría de la singularidad y la geometría algebraica computacional. [a]
BL van der Waerden , Oscar Zariski y André Weil desarrollaron una base para la geometría algebraica basada en el álgebra conmutativa contemporánea , incluida la teoría de la valoración y la teoría de los ideales . Uno de los objetivos era dar un marco riguroso para probar los resultados de la escuela italiana de geometría algebraica . En particular, esta escuela utilizó sistemáticamente la noción de punto genérico sin ninguna definición precisa, que fue dada por primera vez por estos autores durante la década de 1930.
En las décadas de 1950 y 1960, Jean-Pierre Serre y Alexander Grothendieck reformularon los fundamentos haciendo uso de la teoría de la gavilla . Más tarde, aproximadamente a partir de 1960, y en gran medida dirigido por Grothendieck, se elaboró la idea de esquemas , junto con un aparato muy refinado de técnicas homológicas . Después de una década de rápido desarrollo, el campo se estabilizó en la década de 1970 y se realizaron nuevas aplicaciones, tanto a la teoría de números como a cuestiones geométricas más clásicas sobre variedades algebraicas, singularidades , módulos y módulos formales .
Una clase importante de variedades, que no se entiende fácilmente directamente a partir de sus ecuaciones definitorias, son las variedades abelianas , que son las variedades proyectivas cuyos puntos forman un grupo abeliano . Los ejemplos prototípicos son las curvas elípticas , que tienen una rica teoría. Jugaron un papel decisivo en la demostración del último teorema de Fermat y también se utilizan en criptografía de curva elíptica .
Paralelamente a la tendencia abstracta de la geometría algebraica, que se ocupa de enunciados generales sobre variedades, también se han desarrollado métodos para el cálculo efectivo con variedades concretas, lo que condujo a la nueva área de la geometría algebraica computacional. Uno de los métodos fundadores de esta área es la teoría de las bases de Gröbner , introducida por Bruno Buchberger en 1965. Otro método fundador, más especialmente dedicado a la geometría algebraica real, es la descomposición algebraica cilíndrica , introducida por George E. Collins en 1973.
Véanse también: geometría algebraica derivada .
Una variedad analítica se define localmente como el conjunto de soluciones comunes de varias ecuaciones que involucran funciones analíticas . Es análogo al concepto incluido de variedad algebraica real o compleja . Cualquier variedad compleja es una variedad analítica. Dado que las variedades analíticas pueden tener puntos singulares , no todas las variedades analíticas son variedades.
La geometría analítica moderna es esencialmente equivalente a la geometría algebraica real y compleja, como lo ha demostrado Jean-Pierre Serre en su artículo GAGA , cuyo nombre en francés significa geometría algebraica y geometría analítica . Sin embargo, los dos campos siguen siendo distintos, ya que los métodos de prueba son bastante diferentes y la geometría algebraica incluye también la geometría en características finitas .
La geometría algebraica ahora encuentra aplicaciones en estadística , [14] teoría de control , [15] [16] robótica , [17] códigos de corrección de errores , [18] filogenética [19] y modelado geométrico . [20] También hay conexiones con la teoría de cuerdas , [21] teoría de juegos , [22] coincidencias de gráficos , [23] solitones [24] y programación entera . [25]
El propio Khayyam parece haber sido el primero en concebir una teoría general de ecuaciones cúbicas.