En mecánica continua , la tensión es una cantidad física que describe las fuerzas presentes durante la deformación . Por ejemplo, un objeto que se separa, como una banda elástica estirada, está sujeto a tensión de tracción y puede sufrir alargamiento . Un objeto que se junta, como una esponja arrugada, está sujeto a tensión de compresión y puede sufrir acortamiento. [1] [2] Cuanto mayor es la fuerza y menor es el área de la sección transversal del cuerpo sobre el que actúa, mayor es la tensión. La tensión tiene una dimensión de fuerza por área, con unidades SI de newtons por metro cuadrado (N/m 2 ) o pascal (Pa).
La tensión expresa las fuerzas internas que las partículas vecinas de un material continuo ejercen entre sí, mientras que la deformación es la medida de la deformación relativa del material. [3] Por ejemplo, cuando una barra vertical sólida soporta un peso superior , cada partícula en la barra empuja a las partículas inmediatamente debajo de ella. Cuando un líquido está en un recipiente cerrado bajo presión , cada partícula es empujada contra todas las partículas circundantes. Las paredes del recipiente y la superficie que induce presión (como un pistón) empujan contra ellas en una reacción (newtoniana) . Estas fuerzas macroscópicas son en realidad el resultado neto de un gran número de fuerzas intermoleculares y colisiones entre las partículas de esas moléculas . El estrés se representa frecuentemente mediante una letra griega minúscula sigma ( σ ).
La tensión dentro de un material puede surgir por varios mecanismos, como la tensión aplicada por fuerzas externas al material a granel (como la gravedad ) o a su superficie (como fuerzas de contacto , presión externa o fricción ). Cualquier deformación (deformación) de un material sólido genera una tensión elástica interna , análoga a la fuerza de reacción de un resorte , que tiende a restaurar el material a su estado original no deformado. En líquidos y gases , sólo las deformaciones que cambian el volumen generan tensión elástica persistente. Si la deformación cambia gradualmente con el tiempo, incluso en los fluidos suele haber cierta tensión viscosa que se opone a ese cambio. Las tensiones elásticas y viscosas suelen combinarse bajo el nombre de tensión mecánica .

Puede existir una tensión significativa incluso cuando la deformación es insignificante o inexistente (una suposición común al modelar el flujo de agua). El estrés puede existir en ausencia de fuerzas externas; Esta tensión incorporada es importante, por ejemplo, en el hormigón pretensado y el vidrio templado . También se puede imponer tensión a un material sin la aplicación de fuerzas netas , por ejemplo mediante cambios de temperatura o composición química , o mediante campos electromagnéticos externos (como en materiales piezoeléctricos y magnetoestrictivos ).
La relación entre tensión mecánica, deformación y tasa de deformación puede ser bastante complicada, aunque una aproximación lineal puede ser adecuada en la práctica si las cantidades son suficientemente pequeñas. La tensión que excede ciertos límites de resistencia del material dará como resultado una deformación permanente (como flujo plástico , fractura , cavitación ) o incluso cambiará su estructura cristalina y composición química .
Los seres humanos conocen la tensión en el interior de los materiales desde la antigüedad. Hasta el siglo XVII, esta comprensión era en gran medida intuitiva y empírica, aunque esto no impidió el desarrollo de tecnologías relativamente avanzadas como el arco compuesto y el soplado de vidrio . [4]
A lo largo de varios milenios, los arquitectos y los constructores en particular aprendieron a ensamblar vigas de madera y bloques de piedra cuidadosamente moldeados para resistir, transmitir y distribuir las tensiones de la manera más eficaz, con ingeniosos dispositivos como capiteles , arcos , cúpulas , cerchas y los arbotantes de las catedrales góticas .
Los arquitectos antiguos y medievales desarrollaron algunos métodos geométricos y fórmulas simples para calcular los tamaños adecuados de pilares y vigas, pero la comprensión científica de la tensión sólo fue posible después de que se inventaran las herramientas necesarias en los siglos XVII y XVIII: el riguroso experimento experimental de Galileo Galilei. método , las coordenadas y la geometría analítica de René Descartes , y las leyes de movimiento y equilibrio de Newton y el cálculo de infinitesimales . [5] Con esas herramientas, Augustin-Louis Cauchy pudo dar el primer modelo matemático riguroso y general de un cuerpo elástico deformado introduciendo las nociones de tensión y deformación. [6] Cauchy observó que la fuerza a través de una superficie imaginaria era una función lineal de su vector normal; y, además, que debe ser una función simétrica (con impulso total cero). La comprensión de la tensión en los líquidos comenzó con Newton, quien proporcionó una fórmula diferencial para las fuerzas de fricción (esfuerzo cortante) en un flujo laminar paralelo .
La tensión se define como la fuerza a través de un límite pequeño por unidad de área de ese límite, para todas las orientaciones del límite. [7] Derivada de una cantidad física fundamental (fuerza) y de una cantidad puramente geométrica (área), la tensión es también una cantidad fundamental, como la velocidad, el par o la energía , que puede cuantificarse y analizarse sin una consideración explícita de la naturaleza del material. o de sus causas físicas.

Siguiendo las premisas básicas de la mecánica del continuo, el estrés es un concepto macroscópico . Es decir, las partículas consideradas en su definición y análisis deberían ser lo suficientemente pequeñas como para ser tratadas como homogéneas en composición y estado, pero aún lo suficientemente grandes como para ignorar los efectos cuánticos y los movimientos detallados de las moléculas. Así, la fuerza entre dos partículas es en realidad el promedio de un gran número de fuerzas atómicas entre sus moléculas; y se supone que cantidades físicas como la masa, la velocidad y las fuerzas que actúan a través de la masa de los cuerpos tridimensionales, como la gravedad, están suavemente distribuidas sobre ellos. [8] : 90–106 Dependiendo del contexto, también se puede suponer que las partículas son lo suficientemente grandes como para permitir el promedio de otras características microscópicas, como los granos de una varilla de metal o las fibras de un trozo de madera .
Cuantitativamente, la tensión se expresa mediante el vector de tracción de Cauchy T definido como la fuerza de tracción F entre partes adyacentes del material a través de una superficie de separación imaginaria S , dividida por el área de S. [9] : 41–50 En un fluido en reposo, la fuerza es perpendicular a la superficie y es la conocida presión . En un sólido o en un flujo de líquido viscoso , la fuerza F puede no ser perpendicular a S ; por tanto, la tensión a través de una superficie debe considerarse una cantidad vectorial, no escalar. Además, la dirección y la magnitud generalmente dependen de la orientación de S. Así, el estado tensional del material debe ser descrito mediante un tensor , llamado tensor de tensión (Cauchy) ; que es una función lineal que relaciona el vector normal n de una superficie S con el vector de tracción T a través de S. Con respecto a cualquier sistema de coordenadas elegido , el tensor de tensión de Cauchy se puede representar como una matriz simétrica de 3×3 números reales. Incluso dentro de un cuerpo homogéneo , el tensor de tensión puede variar de un lugar a otro y cambiar con el tiempo; por lo tanto, la tensión dentro de un material es, en general, un campo tensorial variable en el tiempo .
En general, la tensión T que una partícula P aplica sobre otra partícula Q a través de una superficie S puede tener cualquier dirección con respecto a S. El vector T puede considerarse como la suma de dos componentes: el esfuerzo normal ( compresión o tensión ) perpendicular a la superficie y el esfuerzo cortante paralelo a la superficie.
Si el vector unitario normal n de la superficie (que apunta desde Q hacia P ) se supone fijo, el componente normal se puede expresar mediante un solo número, el producto escalar T · n . Este número será positivo si P está "tirando" de Q (esfuerzo de tracción) y negativo si P está "empujando" contra Q (esfuerzo de compresión). El componente de corte es entonces el vector T − ( T · n ) n .
La dimensión de la tensión es la de la presión , y por tanto sus coordenadas se miden en las mismas unidades que la presión: a saber, pascales (Pa, es decir, newtons por metro cuadrado ) en el Sistema Internacional , o libras por pulgada cuadrada (psi) en el sistema imperial . Debido a que las tensiones mecánicas superan fácilmente el millón de pascales, MPa, que significa megapascal, es una unidad común de tensión.

El estrés en un cuerpo material puede deberse a múltiples causas físicas, incluidas influencias externas y procesos físicos internos. Algunos de estos agentes (como la gravedad, los cambios de temperatura y fase y los campos electromagnéticos) actúan sobre la mayor parte del material, variando continuamente con la posición y el tiempo. Otros agentes (como cargas externas y fricción, presión ambiental y fuerzas de contacto) pueden crear tensiones y fuerzas que se concentran en ciertas superficies, líneas o puntos; y posiblemente también en intervalos de tiempo muy cortos (como en los impulsos debidos a colisiones). En la materia activa , la autopropulsión de partículas microscópicas genera perfiles de tensión macroscópicos. [11] En general, la distribución de tensiones en un cuerpo se expresa como una función continua por partes del espacio y el tiempo.
Por el contrario, la tensión suele correlacionarse con diversos efectos sobre el material, incluidos posiblemente cambios en propiedades físicas como birrefringencia , polarización y permeabilidad . La imposición de tensión por parte de un agente externo generalmente crea cierta tensión (deformación) en el material, incluso si es demasiado pequeña para ser detectada. En un material sólido, dicha deformación generará a su vez una tensión elástica interna, análoga a la fuerza de reacción de un resorte estirado , que tenderá a restaurar el material a su estado original no deformado. Los materiales fluidos (líquidos, gases y plasmas ) por definición sólo pueden resistir deformaciones que cambiarían su volumen. Si la deformación cambia con el tiempo, incluso en los fluidos suele haber cierta tensión viscosa que se opone a ese cambio. Estas tensiones pueden ser de naturaleza normal o cortante. El origen molecular de las tensiones cortantes en los fluidos se proporciona en el artículo sobre viscosidad . Lo mismo para las tensiones viscosas normales se puede encontrar en Sharma (2019). [12]
La relación entre la tensión y sus efectos y causas, incluida la deformación y la tasa de cambio de deformación, puede ser bastante complicada (aunque una aproximación lineal puede ser adecuada en la práctica si las cantidades son lo suficientemente pequeñas). La tensión que excede ciertos límites de resistencia del material dará como resultado una deformación permanente (como flujo plástico , fractura , cavitación ) o incluso cambiará su estructura cristalina y composición química .
En algunas situaciones, la tensión dentro de un cuerpo puede describirse adecuadamente mediante un único número o mediante un único vector (un número y una dirección). Tres de estas situaciones de tensión simples , que se encuentran a menudo en el diseño de ingeniería, son la tensión normal uniaxial , la tensión cortante simple y la tensión normal isotrópica . [13]

Una situación común con un patrón de tensiones simple es cuando una varilla recta, con material y sección transversal uniforme, se somete a tensión por fuerzas opuestas de magnitud a lo largo de su eje. Si el sistema está en equilibrio y no cambia con el tiempo, y el peso de la barra puede despreciarse, entonces a través de cada sección transversal de la barra la parte superior debe tirar de la parte inferior con la misma fuerza, F con continuidad a través de toda la barra. área de la sección transversal , A. Por lo tanto, la tensión σ a lo largo de la barra, a través de cualquier superficie horizontal, se puede expresar simplemente mediante el número único σ, calculado simplemente con la magnitud de esas fuerzas, F , y el área de la sección transversal , A.

Este análisis supone que la tensión se distribuye uniformemente en toda la sección transversal. En la práctica, dependiendo de cómo se une la barra en los extremos y de cómo se fabricó, esta suposición puede no ser válida. En ese caso, el valor = F / A será sólo la tensión promedio, llamada tensión de ingeniería o tensión nominal . Si la longitud L de la barra es muchas veces su diámetro D y no tiene defectos importantes ni tensión incorporada, entonces se puede suponer que la tensión está distribuida uniformemente sobre cualquier sección transversal que sea más de unas pocas veces D en ambos extremos. . (Esta observación se conoce como principio de Saint-Venant ).
La tensión normal ocurre en muchas otras situaciones además de la tensión y compresión axial. Si una barra elástica con sección transversal uniforme y simétrica se dobla en uno de sus planos de simetría, la tensión de flexión resultante seguirá siendo normal (perpendicular a la sección transversal), pero variará a lo largo de la sección transversal: la parte exterior estará bajo tensión de tracción, mientras que la parte interior estará comprimida. Otra variante de la tensión normal es la tensión circular que se produce en las paredes de una tubería o recipiente cilíndrico lleno de fluido a presión.

Otro tipo simple de tensión ocurre cuando una capa uniformemente gruesa de material elástico como pegamento o caucho está firmemente unida a dos cuerpos rígidos que son arrastrados en direcciones opuestas por fuerzas paralelas a la capa; o una sección de una barra de metal blando que se corta con las mandíbulas de una herramienta similar a una tijera . Sea F la magnitud de esas fuerzas y M el plano medio de esa capa. Al igual que en el caso de tensión normal, la parte de la capa en un lado de M debe tirar de la otra parte con la misma fuerza F. Suponiendo que se conoce la dirección de las fuerzas, la tensión a través de M se puede expresar simplemente mediante el número único , calculado simplemente con la magnitud de esas fuerzas, F y el área de la sección transversal, A.
Como en el caso de una barra cargada axialmente, en la práctica el esfuerzo cortante puede no distribuirse uniformemente sobre la capa; entonces, como antes, la relación F / A será solo una tensión promedio ("nominal", "de ingeniería"). Ese promedio suele ser suficiente a efectos prácticos. [14] : 292 El esfuerzo cortante también se observa cuando una barra cilíndrica, como un eje, se somete a pares opuestos en sus extremos. En ese caso, el esfuerzo cortante en cada sección transversal es paralelo a la sección transversal, pero está orientado tangencialmente con respecto al eje y aumenta con la distancia desde el eje. Se produce un esfuerzo cortante significativo en la placa intermedia (el "alma") de las vigas en I bajo cargas de flexión, debido a que el alma constriñe las placas extremas ("bridas").
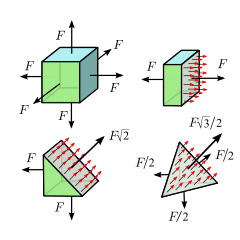
Otro tipo simple de tensión ocurre cuando el cuerpo material está bajo igual compresión o tensión en todas las direcciones. Este es el caso, por ejemplo, de una porción de líquido o gas en reposo, ya sea encerrada en algún recipiente o como parte de una masa mayor de fluido; o dentro de un cubo de material elástico que está siendo presionado o tirado en las seis caras por fuerzas perpendiculares iguales, siempre que, en ambos casos, el material sea homogéneo, sin tensión incorporada y que el efecto de la gravedad y otras fuerzas externas puede ser descuidado.
En estas situaciones, la tensión a través de cualquier superficie interna imaginaria resulta ser igual en magnitud y siempre dirigida perpendicularmente a la superficie independientemente de la orientación de la superficie. Este tipo de estrés puede denominarse normal isotrópico o simplemente isotrópico ; si es compresiva se llama presión hidrostática o simplemente presión . Los gases, por definición, no pueden resistir tensiones de tracción, pero algunos líquidos pueden soportar cantidades muy grandes de tensiones de tracción isotrópicas en algunas circunstancias. ver tubo Z.
Las piezas con simetría rotacional , como ruedas, ejes, tuberías y pilares, son muy comunes en ingeniería. A menudo, los patrones de tensión que se producen en dichas piezas tienen simetría rotacional o incluso cilíndrica . El análisis de tales tensiones cilíndricas puede aprovechar la simetría para reducir la dimensión del dominio y/o del tensor de tensiones.
A menudo, los cuerpos mecánicos experimentan más de un tipo de tensión al mismo tiempo; esto se llama estrés combinado . En tensión normal y cortante, la magnitud de la tensión es máxima para superficies que son perpendiculares a una determinada dirección y cero en cualquier superficie que sea paralela a . Cuando el esfuerzo cortante es cero solo en superficies que son perpendiculares a una dirección particular, el esfuerzo se llama biaxial y puede verse como la suma de dos esfuerzos normales o cortantes. En el caso más general, llamado tensión triaxial , la tensión es distinta de cero en todos los elementos de la superficie.


Las tensiones combinadas no pueden describirse mediante un único vector. Incluso si el material se esfuerza de la misma manera en todo el volumen del cuerpo, la tensión a través de cualquier superficie imaginaria dependerá de la orientación de esa superficie, de una manera no trivial.
Cauchy observó que el vector de tensión a través de una superficie siempre será una función lineal del vector normal de la superficie , el vector de longitud unitaria que es perpendicular a ella. Es decir, donde la función satisface
Como cualquier mapa lineal entre vectores, el tensor de tensión se puede representar en cualquier sistema de coordenadas cartesiano elegido mediante una matriz de números reales de 3×3. Dependiendo de si las coordenadas están numeradas o nombradas , la matriz se puede escribir como
La relación lineal entre y se deriva de las leyes fundamentales de conservación del momento lineal y del equilibrio estático de fuerzas y, por lo tanto, es matemáticamente exacta para cualquier material y cualquier situación de tensión. Los componentes del tensor de tensión de Cauchy en cada punto de un material satisfacen las ecuaciones de equilibrio ( ecuaciones de movimiento de Cauchy para aceleración cero). Además, el principio de conservación del momento angular implica que el tensor de tensión es simétrico , es decir , y . Por lo tanto, el estado de tensión del medio en cualquier punto e instante puede especificarse mediante sólo seis parámetros independientes, en lugar de nueve. Estos pueden estar escritos
El tensor de tensión de Cauchy obedece a la ley de transformación del tensor ante un cambio en el sistema de coordenadas. Una representación gráfica de esta ley de transformación es el círculo de distribución de tensiones de Mohr .
Como matriz real simétrica de 3 × 3, el tensor de tensión tiene tres vectores propios de longitud unitaria mutuamente ortogonales y tres valores propios reales , tales que . Por lo tanto, en un sistema de coordenadas con ejes , el tensor de tensión es una matriz diagonal y tiene solo los tres componentes normales λ 1 , λ 2 , λ 3 {\displaystyle \lambda _{1},\lambda _{2},\ lambda _{3}} las tensiones principales . Si los tres valores propios son iguales, la tensión es una compresión o tensión isotrópica , siempre perpendicular a cualquier superficie, no hay tensión cortante y el tensor es una matriz diagonal en cualquier sistema de coordenadas.
En general, la tensión no se distribuye uniformemente sobre un cuerpo material y puede variar con el tiempo. Por lo tanto, el tensor de tensiones debe definirse para cada punto y cada momento, considerando una partícula infinitesimal del medio que rodea ese punto y tomando las tensiones promedio en esa partícula como las tensiones en el punto.

Los objetos hechos por el hombre a menudo se fabrican a partir de placas de diversos materiales mediante operaciones que no cambian su carácter esencialmente bidimensional, como cortar, taladrar, doblar suavemente y soldar a lo largo de los bordes. La descripción de la tensión en tales cuerpos se puede simplificar modelando esas partes como superficies bidimensionales en lugar de cuerpos tridimensionales.
Desde ese punto de vista, se redefine una "partícula" como un parche infinitesimal de la superficie de la placa, de modo que el límite entre partículas adyacentes se convierte en un elemento lineal infinitesimal; ambos están implícitamente extendidos en la tercera dimensión, normal a (directamente a través) de la placa. Luego, la "tensión" se redefine como una medida de las fuerzas internas entre dos "partículas" adyacentes a través de su elemento lineal común, dividida por la longitud de esa línea. Algunos componentes del tensor de tensión pueden ignorarse, pero como las partículas no son infinitesimales en la tercera dimensión, ya no se puede ignorar el torque que una partícula aplica a sus vecinas. Ese par se modela como un esfuerzo de flexión que tiende a cambiar la curvatura de la placa. Es posible que estas simplificaciones no se apliquen en soldaduras, curvas cerradas y pliegues (donde el radio de curvatura es comparable al espesor de la placa).

El análisis de tensiones puede simplificarse considerablemente también para barras, vigas o alambres delgados de composición y sección transversal uniformes (o que varían suavemente) que están sujetos a flexión y torsión moderadas. Para esos cuerpos, se pueden considerar sólo secciones transversales que sean perpendiculares al eje de la barra y redefinir una "partícula" como un trozo de alambre con una longitud infinitesimal entre dos de esas secciones transversales. El esfuerzo ordinario se reduce entonces a un escalar (tensión o compresión de la barra), pero hay que tener en cuenta también un esfuerzo de flexión (que intenta cambiar la curvatura de la barra, en alguna dirección perpendicular al eje) y un esfuerzo de torsión ( que intenta girarlo o desenroscarlo sobre su eje).
El análisis de tensiones es una rama de la física aplicada que cubre la determinación de la distribución interna de fuerzas internas en objetos sólidos. Es una herramienta esencial en ingeniería para el estudio y diseño de estructuras como túneles, presas, piezas mecánicas y marcos estructurales, bajo cargas prescritas o esperadas. También es importante en muchas otras disciplinas; por ejemplo, en geología, para estudiar fenómenos como la tectónica de placas , el vulcanismo y los aludes ; y en biología, para comprender la anatomía de los seres vivos.
El análisis de tensiones generalmente se ocupa de objetos y estructuras que se puede suponer que están en equilibrio estático macroscópico . Según las leyes del movimiento de Newton , cualquier fuerza externa que se aplique a dicho sistema debe estar equilibrada por fuerzas de reacción internas, [15] : 97 que casi siempre son fuerzas de contacto superficial entre partículas adyacentes, es decir, como tensión. [9] Dado que cada partícula necesita estar en equilibrio, esta reacción de estrés generalmente se propagará de una partícula a otra, creando una distribución de estrés por todo el cuerpo. El problema típico en el análisis de tensiones es determinar estas tensiones internas, dadas las fuerzas externas que actúan sobre el sistema. Estas últimas pueden ser fuerzas corporales (como la gravedad o la atracción magnética), que actúan en todo el volumen de un material; [16] : 42–81 o cargas concentradas (como la fricción entre un eje y un rodamiento , o el peso de una rueda de tren sobre un riel), que se imagina que actúan sobre un área bidimensional, o a lo largo de una línea, o en un solo punto.
En el análisis de tensiones normalmente se ignoran las causas físicas de las fuerzas o la naturaleza precisa de los materiales. En cambio, se supone que las tensiones están relacionadas con la deformación (y, en problemas no estáticos, con la velocidad de deformación) del material mediante ecuaciones constitutivas conocidas . [17]
El análisis de tensiones se puede llevar a cabo experimentalmente, aplicando cargas al artefacto real o a un modelo a escala, y midiendo las tensiones resultantes, mediante cualquiera de los varios métodos disponibles. Este enfoque se utiliza a menudo para la certificación y el seguimiento de la seguridad. La mayor parte de la tensión se analiza mediante métodos matemáticos, especialmente durante el diseño. El problema básico del análisis de tensiones puede formularse mediante las ecuaciones de movimiento de Euler para cuerpos continuos (que son consecuencias de las leyes de Newton para la conservación del momento lineal y del momento angular ) y el principio de tensión de Euler-Cauchy , junto con las ecuaciones constitutivas apropiadas. De esta manera se obtiene un sistema de ecuaciones diferenciales parciales que involucran el campo tensor de tensión y el campo tensor de deformación , como funciones desconocidas por determinar. Las fuerzas externas del cuerpo aparecen como el término independiente ("lado derecho") en las ecuaciones diferenciales, mientras que las fuerzas concentradas aparecen como condiciones de contorno. Por lo tanto, el problema básico del análisis de tensiones es un problema de valores en la frontera .
El análisis de tensiones para estructuras elásticas se basa en la teoría de la elasticidad y la teoría de la deformación infinitesimal . Cuando las cargas aplicadas causan deformación permanente, se deben utilizar ecuaciones constitutivas más complicadas, que puedan dar cuenta de los procesos físicos involucrados ( flujo plástico , fractura , cambio de fase , etc.). Las estructuras de ingeniería generalmente se diseñan de modo que las tensiones máximas esperadas estén dentro del rango de elasticidad lineal (la generalización de la ley de Hooke para medios continuos); es decir, las deformaciones provocadas por tensiones internas están relacionadas linealmente con ellas. En este caso las ecuaciones diferenciales que definen el tensor de tensiones son lineales y el problema se vuelve mucho más sencillo. Por un lado, la tensión en cualquier punto también será una función lineal de las cargas. Para tensiones suficientemente pequeñas, generalmente se puede suponer que incluso los sistemas no lineales son lineales.

El análisis de tensiones se simplifica cuando las dimensiones físicas y la distribución de cargas permiten tratar la estructura como unidimensional o bidimensional. En el análisis de armaduras, por ejemplo, se puede suponer que el campo de esfuerzos es uniforme y uniaxial sobre cada miembro. Luego, las ecuaciones diferenciales se reducen a un conjunto finito de ecuaciones (generalmente lineales) con un número finito de incógnitas. En otros contextos, es posible reducir el problema tridimensional a uno bidimensional y/o reemplazar los tensores generales de tensión y deformación por modelos más simples como tensión/compresión uniaxial, corte simple, etc.
Aún así, para casos bidimensionales o tridimensionales se debe resolver un problema de ecuación diferencial parcial. Se pueden obtener soluciones analíticas o de forma cerrada de las ecuaciones diferenciales cuando la geometría, las relaciones constitutivas y las condiciones de frontera son lo suficientemente simples. De lo contrario, generalmente se debe recurrir a aproximaciones numéricas como el método de los elementos finitos , el método de las diferencias finitas y el método de los elementos límite .
Otras medidas de tensión útiles incluyen el primer y segundo tensor de tensión de Piola-Kirchhoff , el tensor de tensión de Biot y el tensor de tensión de Kirchhoff .