Anillo conmutativo

Estructura algebraica

En matemáticas , un anillo conmutativo es un anillo en el que la operación de multiplicación es conmutativa . El estudio de los anillos conmutativos se denomina álgebra conmutativa . Complementariamente, el álgebra no conmutativa es el estudio de las propiedades de los anillos que no son específicas de los anillos conmutativos. Esta distinción resulta del alto número de propiedades fundamentales de los anillos conmutativos que no se extienden a los anillos no conmutativos.

Definición y primeros ejemplos

Definición

Un anillo es un conjunto dotado de dos operaciones binarias , es decir, operaciones que combinan dos elementos cualesquiera del anillo para formar un tercero. Se denominan adición y multiplicación y se denotan comúnmente por " " y " "; p. ej . y . Para formar un anillo, estas dos operaciones deben satisfacer una serie de propiedades: el anillo debe ser un grupo abeliano en la adición, así como un monoide en la multiplicación, donde la multiplicación se distribuye sobre la adición; es decir, . Los elementos identidad para la adición y la multiplicación se denotan y , respectivamente. ${\displaystyle R}$ ${\displaystyle +}$ ${\displaystyle \cdot }$ ${\displaystyle a+b}$ ${\displaystyle a\cdot b}$ ${\displaystyle a\cdot \left(b+c\right)=\left(a\cdot b\right)+\left(a\cdot c\right)}$ ${\displaystyle 0}$ ${\displaystyle 1}$

Si la multiplicación es conmutativa, es decir, entonces el anillo se llama conmutativo . En el resto de este artículo, todos los anillos serán conmutativos, a menos que se indique explícitamente lo contrario. $${\displaystyle a\cdot b=b\cdot a,}$$ ${\displaystyle R}$

Primeros ejemplos

Un ejemplo importante, y en cierto sentido crucial, es el anillo de números enteros con las dos operaciones de suma y multiplicación. Como la multiplicación de números enteros es una operación conmutativa, se trata de un anillo conmutativo. Suele denotarse como una abreviatura de la palabra alemana Zahlen (números). ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$

Un cuerpo es un anillo conmutativo donde y todo elemento distinto de cero es invertible, es decir, tiene un inverso multiplicativo tal que . Por lo tanto, por definición, cualquier cuerpo es un anillo conmutativo. Los números racionales , reales y complejos forman cuerpos. ${\displaystyle 0\not =1}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a\cdot b=1}$

Si es un anillo conmutativo dado, entonces el conjunto de todos los polinomios en la variable cuyos coeficientes están en forma el anillo polinomial , denotado . Lo mismo es válido para varias variables. ${\displaystyle R}$ ${\displaystyle X}$ ${\displaystyle R}$ ${\displaystyle R\left[X\right]}$

Si es un espacio topológico , por ejemplo un subconjunto de algunas funciones continuas de valor real o complejo en forman un anillo conmutativo. Lo mismo es cierto para funciones diferenciables u holomorfas , cuando se definen los dos conceptos, como para una variedad compleja . ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle V}$ ${\displaystyle V}$

Divisibilidad

A diferencia de los cuerpos, donde todo elemento distinto de cero es multiplicativamente invertible, el concepto de divisibilidad para los anillos es más rico. Un elemento de un anillo se denomina unidad si posee un inverso multiplicativo. Otro tipo particular de elemento son los divisores de cero , es decir, un elemento tal que existe un elemento distinto de cero del anillo tal que . Si no posee divisores de cero distintos de cero, se denomina dominio integral (o dominio). Un elemento que satisface para algún entero positivo se denomina nilpotente . ${\displaystyle a}$ ${\displaystyle R}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle ab=0}$ ${\displaystyle R}$ ${\displaystyle a}$ ${\displaystyle a^{n}=0}$ ${\displaystyle n}$

Localizaciones

La localización de un anillo es un proceso en el que algunos elementos se vuelven invertibles, es decir, se añaden inversos multiplicativos al anillo. Concretamente, si es un subconjunto multiplicativamente cerrado de (es decir, siempre que entonces también lo es ) entonces la localización de en , o anillo de fracciones con denominadores en , normalmente denotado consta de símbolos ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle s,t\in S}$ ${\displaystyle st}$ ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S^{-1}R}$

${\displaystyle {\frac {r}{s}}}$con ${\displaystyle r\in R,s\in S}$

sujeto a ciertas reglas que imitan la cancelación familiar de los números racionales. De hecho, en este lenguaje es la localización de todos los enteros distintos de cero. Esta construcción funciona para cualquier dominio integral en lugar de . La localización es un campo, llamado el campo cociente de . ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle R}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \left(R\setminus \left\{0\right\}\right)^{-1}R}$ ${\displaystyle R}$

Ideales y módulos

Muchos de los conceptos siguientes también existen para anillos no necesariamente conmutativos, pero las definiciones y propiedades suelen ser más complicadas. Por ejemplo, todos los ideales en un anillo conmutativo son automáticamente bilaterales , lo que simplifica considerablemente la situación.

Módulos

Para un anillo , un módulo es como lo que un espacio vectorial es para un cuerpo. Es decir, los elementos de un módulo se pueden sumar; se pueden multiplicar por elementos de sujeto a los mismos axiomas que para un espacio vectorial. ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle R}$

El estudio de los módulos es significativamente más complejo que el de los espacios vectoriales , ya que existen módulos que no tienen base , es decir, no contienen un conjunto generador cuyos elementos sean linealmente independientes . Un módulo que tiene base se denomina módulo libre , y un submódulo de un módulo libre no necesita ser libre.

Un módulo de tipo finito es un módulo que tiene un conjunto generador finito. Los módulos de tipo finito juegan un papel fundamental en la teoría de anillos conmutativos, similar al papel de los espacios vectoriales de dimensión finita en el álgebra lineal . En particular, los anillos noetherianos (véase también § Anillos noetherianos , más abajo) pueden definirse como los anillos tales que cada submódulo de un módulo de tipo finito es también de tipo finito.

Ideales

Los ideales de un anillo son los submódulos de , es decir, los módulos contenidos en . En más detalle, un ideal es un subconjunto no vacío de tal que para todos en , y en , tanto y están en . Para diversas aplicaciones, comprender los ideales de un anillo es de particular importancia, pero a menudo se procede estudiando los módulos en general. ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle I}$ ${\displaystyle ri}$ ${\displaystyle i+j}$ ${\displaystyle I}$

Cualquier anillo tiene dos ideales, a saber, el ideal cero y , el anillo completo. Estos dos ideales son los únicos precisamente si es un cuerpo. Dado cualquier subconjunto de (donde es un conjunto índice), el ideal generado por es el ideal más pequeño que contiene a . Equivalentemente, está dado por combinaciones lineales finitas ${\displaystyle \left\{0\right\}}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle F=\left\{f_{j}\right\}_{j\in J}}$ ${\displaystyle R}$ ${\displaystyle J}$ ${\displaystyle F}$ ${\displaystyle F}$ $${\displaystyle r_{1}f_{1}+r_{2}f_{2}+\dots +r_{n}f_{n}.}$$

Principales dominios ideales

Si consta de un solo elemento , el ideal generado por consta de los múltiplos de , es decir, los elementos de la forma para elementos arbitrarios . Un ideal de este tipo se llama ideal principal . Si todo ideal es un ideal principal, se llama anillo de ideales principales ; dos casos importantes son y , el anillo de polinomios sobre un cuerpo . Estos dos son además dominios, por lo que se llaman dominios de ideales principales . ${\displaystyle F}$ ${\displaystyle r}$ ${\displaystyle F}$ ${\displaystyle r}$ ${\displaystyle rs}$ ${\displaystyle s}$ ${\displaystyle R}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle k\left[X\right]}$ ${\displaystyle k}$

A diferencia de los anillos generales, para un dominio ideal principal, las propiedades de los elementos individuales están fuertemente ligadas a las propiedades del anillo como un todo. Por ejemplo, cualquier dominio ideal principal es un dominio de factorización única (UFD), lo que significa que cualquier elemento es un producto de elementos irreducibles, de una manera única (hasta reordenar los factores). Aquí, un elemento en un dominio se llama irreducible si la única manera de expresarlo como un producto es ya sea o siendo una unidad. Un ejemplo, importante en la teoría de campos , son los polinomios irreducibles , es decir, elementos irreducibles en , para un campo . El hecho de que sea un UFD se puede expresar de manera más elemental diciendo que cualquier número natural se puede descomponer de manera única como producto de potencias de números primos. También se conoce como el teorema fundamental de la aritmética . ${\displaystyle R}$ ${\displaystyle a}$ $${\displaystyle a=bc,}$$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle k\left[X\right]}$ ${\displaystyle k}$ ${\displaystyle \mathbb {Z} }$

Un elemento es primo si siempre que divide un producto , divide o . En un dominio, ser primo implica ser irreducible. Lo inverso es cierto en un dominio de factorización única, pero falso en general. ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle bc}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

Anillo de factor

La definición de ideales es tal que "dividir" "hacia fuera" da otro anillo, el anillo de factores : es el conjunto de clases laterales de junto con las operaciones y . Por ejemplo, el anillo (también denotado ), donde es un entero, es el anillo de números enteros módulo . Es la base de la aritmética modular . ${\displaystyle I}$ ${\displaystyle R/I}$ ${\displaystyle I}$ $${\displaystyle \left(a+I\right)+\left(b+I\right)=\left(a+b\right)+I}$$ ${\displaystyle \left(a+I\right)\left(b+I\right)=ab+I}$ ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ ${\displaystyle \mathbb {Z} _{n}}$ ${\displaystyle n}$ ${\displaystyle n}$

Un ideal es propio si es estrictamente menor que el anillo completo. Un ideal que no está estrictamente contenido en ningún ideal propio se llama maximal . Un ideal es maximal si y solo si es un cuerpo. A excepción del anillo cero , cualquier anillo (con identidad) posee al menos un ideal maximal; esto se deduce del lema de Zorn . ${\displaystyle m}$ ${\displaystyle R/m}$

Anillos noetherianos

Un anillo se llama noetheriano (en honor a Emmy Noether , quien desarrolló este concepto) si cada cadena ascendente de ideales se vuelve estacionaria, es decir, se vuelve constante más allá de algún índice . De manera equivalente, cualquier ideal es generado por un número finito de elementos o, aún equivalente, los submódulos de módulos finitamente generados son finitamente generados. $${\displaystyle 0\subseteq I_{0}\subseteq I_{1}\subseteq \dots \subseteq I_{n}\subseteq I_{n+1}\dots }$$ ${\displaystyle n}$

Ser noetheriano es una condición de finitud muy importante, y la condición se conserva bajo muchas operaciones que ocurren con frecuencia en geometría. Por ejemplo, si es noetheriano, entonces también lo es el anillo de polinomios (por el teorema de la base de Hilbert ), cualquier localización y también cualquier anillo de factores . ${\displaystyle R}$ ${\displaystyle R\left[X_{1},X_{2},\dots ,X_{n}\right]}$ ${\displaystyle S^{-1}R}$ ${\displaystyle R/I}$

Cualquier anillo no noetheriano es la unión de sus subanillos noetherianos. Este hecho, conocido como aproximación noetheriana, permite la extensión de ciertos teoremas a anillos no noetherianos. ${\displaystyle R}$

Anillos artinianos

Un anillo se llama artiniano (en honor a Emil Artin ) si cada cadena descendente de ideales se vuelve estacionaria en algún momento. A pesar de que las dos condiciones parecen simétricas, los anillos noetherianos son mucho más generales que los anillos artinianos. Por ejemplo, es noetheriano, ya que cada ideal puede ser generado por un elemento, pero no es artiniano, como lo muestra la cadena. De hecho, por el teorema de Hopkins-Levitzki , cada anillo artiniano es noetheriano. Más precisamente, los anillos artinianos pueden caracterizarse como los anillos noetherianos cuya dimensión de Krull es cero. $${\displaystyle R\supseteq I_{0}\supseteq I_{1}\supseteq \dots \supseteq I_{n}\supseteq I_{n+1}\dots }$$ ${\displaystyle \mathbb {Z} }$ $${\displaystyle \mathbb {Z} \supsetneq 2\mathbb {Z} \supsetneq 4\mathbb {Z} \supsetneq 8\mathbb {Z} \dots }$$

Espectro de un anillo conmutativo

Ideales primordiales

Como se mencionó anteriormente, es un dominio de factorización único . Esto no es cierto para anillos más generales, como se dieron cuenta los algebristas en el siglo XIX. Por ejemplo, en hay dos formas genuinamente distintas de escribir 6 como un producto: Los ideales primos, a diferencia de los elementos primos, proporcionan una forma de evitar este problema. Un ideal primo es un ideal propio (es decir, estrictamente contenido en ) tal que, siempre que el producto de dos elementos del anillo y esté en al menos uno de los dos elementos ya está en (La conclusión opuesta se aplica a cualquier ideal, por definición). Por lo tanto, si un ideal primo es principal, es generado de manera equivalente por un elemento primo. Sin embargo, en anillos como los ideales primos no necesitan ser principales. Esto limita el uso de elementos primos en la teoría de anillos. Sin embargo, una piedra angular de la teoría de números algebraicos es el hecho de que en cualquier anillo de Dedekind (que incluye y, de manera más general, el anillo de números enteros en un cuerpo numérico ) cualquier ideal (como el generado por 6) se descompone de manera única como un producto de ideales primos. ${\displaystyle \mathbb {Z} }$ $${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right]}$$ $${\displaystyle 6=2\cdot 3=\left(1+{\sqrt {-5}}\right)\left(1-{\sqrt {-5}}\right).}$$ ${\displaystyle R}$ ${\displaystyle p}$ ${\displaystyle ab}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle p,}$ ${\displaystyle p.}$ ${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right],}$ ${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right]}$

Cualquier ideal maximal es un ideal primo o, más brevemente, es primo. Además, un ideal es primo si y solo si el anillo de factores es un dominio integral. Demostrar que un ideal es primo, o equivalentemente que un anillo no tiene divisores de cero, puede ser muy difícil. Otra forma de expresarlo es decir que el complemento es multiplicativamente cerrado. La localización es lo suficientemente importante como para tener su propia notación: . Este anillo tiene solo un ideal maximal, a saber . Dichos anillos se denominan locales . ${\displaystyle I}$ ${\displaystyle R/I}$ ${\displaystyle R\setminus p}$ ${\displaystyle \left(R\setminus p\right)^{-1}R}$ ${\displaystyle R_{p}}$ ${\displaystyle pR_{p}}$

Espectro

Spec ( Z ) contiene un punto para el ideal cero. El cierre de este punto es todo el espacio. Los puntos restantes son los correspondientes a los ideales ( p ), donde p es un número primo. Estos puntos son cerrados.

El espectro de un anillo , ^[a] denotado por , es el conjunto de todos los ideales primos de . Está equipado con una topología, la topología de Zariski , que refleja las propiedades algebraicas de : una base de subconjuntos abiertos viene dada por donde es cualquier elemento del anillo. Interpretado como una función que toma el valor f mod p (es decir, la imagen de f en el cuerpo de residuos R / p ), este subconjunto es el lugar geométrico donde f es distinto de cero. El espectro también hace precisa la intuición de que los anillos de localización y factor son complementarios: las funciones naturales R → R _f y R → R / fR corresponden, después de dotar a los espectros de los anillos en cuestión con su topología de Zariski, a inmersiones complementarias abiertas y cerradas respectivamente. Incluso para anillos básicos, como los ilustrados para R = Z a la derecha, la topología de Zariski es bastante diferente de la del conjunto de números reales. ${\displaystyle R}$ ${\displaystyle {\text{Spec}}\ R}$ ${\displaystyle R}$ ${\displaystyle R}$ $${\displaystyle D\left(f\right)=\left\{p\in {\text{Spec}}\ R,f\not \in p\right\},}$$ ${\displaystyle f}$ ${\displaystyle f}$

El espectro contiene el conjunto de ideales máximos, que ocasionalmente se denota mSpec ( R ). Para un campo algebraicamente cerrado k , mSpec (k[ T ₁ , ..., T _n ] / ( f ₁ , ..., f _m )) está en biyección con el conjunto

{ x = ( x ₁ , ..., x _n ) ∊ k ⁿ

Así, los ideales maximales reflejan las propiedades geométricas de los conjuntos solución de polinomios, lo que constituye una motivación inicial para el estudio de los anillos conmutativos. Sin embargo, la consideración de ideales no maximales como parte de las propiedades geométricas de un anillo es útil por varias razones. Por ejemplo, los ideales primos mínimos (es decir, los que no contienen estrictamente a los más pequeños) corresponden a los componentes irreducibles de Spec R . Para un anillo noetheriano R , Spec R tiene solo un número finito de componentes irreducibles. Esta es una reformulación geométrica de la descomposición primaria , según la cual cualquier ideal puede descomponerse como un producto de un número finito de ideales primarios . Este hecho es la generalización última de la descomposición en ideales primos en los anillos de Dedekind.

Esquemas afines

La noción de espectro es la base común del álgebra conmutativa y la geometría algebraica . La geometría algebraica procede dotando a Spec R de un haz (una entidad que recoge funciones definidas localmente, es decir, en subconjuntos abiertos variables). El dato del espacio y el haz se denomina esquema afín . Dado un esquema afín, el anillo subyacente R puede recuperarse como las secciones globales de . Además, esta correspondencia biunívoca entre anillos y esquemas afines también es compatible con homomorfismos de anillos: cualquier f  : R → S da lugar a una función continua en la dirección opuesta. ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$

Spec S → Spec R , q ↦ f ⁻¹ ( q ), es decir, cualquier ideal primo de S se asigna a su preimagen bajo f , que es un ideal primo de R .

La equivalencia resultante de las dos categorías mencionadas refleja adecuadamente las propiedades algebraicas de los anillos de manera geométrica.

De manera similar al hecho de que las variedades están dadas localmente por subconjuntos abiertos de R ⁿ , los esquemas afines son modelos locales para esquemas , que son el objeto de estudio en geometría algebraica. Por lo tanto, varias nociones sobre anillos conmutativos surgen de la intuición geométrica.

Dimensión

La dimensión de Krull (o dimensión) dim R de un anillo R mide el "tamaño" de un anillo, en términos generales, contando los elementos independientes en R. La dimensión de las álgebras sobre un cuerpo k se puede axiomatizar mediante cuatro propiedades:

• La dimensión es una propiedad local: dim R = sup _{p ∊ Spec R} dim R _p .
• La dimensión es independiente de los elementos nilpotentes: si I ⊆ R es nilpotente entonces dim R = dim R / I .
• La dimensión permanece constante bajo una extensión finita: si S es una R -álgebra que se genera finitamente como un R -módulo, entonces dim S = dim R.
• La dimensión está calibrada por dim k [ X ₁ , ..., X _n ] = n . Este axioma está motivado por considerar el anillo polinomial en n variables como un análogo algebraico del espacio n -dimensional .

La dimensión se define, para cualquier anillo R , como el supremo de longitudes n de cadenas de ideales primos.

p ₀ ⊊ p ₁ ⊊ ... ⊊ p _n .

Por ejemplo, un cuerpo es cero-dimensional, ya que el único ideal primo es el ideal cero. Los enteros son unidimensionales, ya que las cadenas son de la forma (0) ⊊ ( p ), donde p es un número primo . Para anillos no noetherianos, y también anillos no locales, la dimensión puede ser infinita, pero los anillos locales noetherianos tienen dimensión finita. Entre los cuatro axiomas anteriores, los dos primeros son consecuencias elementales de la definición, mientras que los dos restantes dependen de hechos importantes del álgebra conmutativa , el teorema de ascenso y el teorema del ideal principal de Krull .

Homomorfismos de anillos

Un homomorfismo de anillo o, más coloquialmente, simplemente una función , es una función f  : R → S tal que

f ( a + b ) = f ( a ) + f ( b ), f ( ab ) = f ( a ) f ( b ) y f (1) = 1.

Estas condiciones aseguran que f (0) = 0. De manera similar a otras estructuras algebraicas, un homomorfismo de anillo es, por lo tanto, una función compatible con la estructura de los objetos algebraicos en cuestión. En tal situación, S también se denomina R -álgebra, entendiendo que s en S puede multiplicarse por algún r de R , estableciendo

r · s  := f ( r )· s .

El núcleo y la imagen de f se definen por ker( f ) = { r ∈ R , f ( r ) = 0} e im( f ) = f ( R ) = { f ( r ), r ∈ R } . El núcleo es un ideal de R , y la imagen es un subanillo de S .

Un homomorfismo de anillo se denomina isomorfismo si es biyectivo. Un ejemplo de isomorfismo de anillo, conocido como teorema del resto chino , es donde n = p ₁ p ₂ ... p _k es un producto de números primos distintos por pares . $${\displaystyle \mathbf {Z} /n=\bigoplus _{i=0}^{k}\mathbf {Z} /p_{i},}$$

Los anillos conmutativos, junto con los homomorfismos de anillos, forman una categoría . El anillo Z es el objeto inicial de esta categoría, lo que significa que para cualquier anillo conmutativo R , existe un único homomorfismo de anillo Z → R . Por medio de esta función, un entero n puede considerarse como un elemento de R . Por ejemplo, la fórmula binomial que es válida para dos elementos cualesquiera a y b en cualquier anillo conmutativo R se entiende en este sentido interpretando los coeficientes binomiales como elementos de R utilizando esta función. $${\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}}$$

La propiedad universal de S ⊗ _R T establece que para dos mapas cualesquiera S → W y T → W que hacen conmutar el cuadrángulo exterior, hay un mapa único S ⊗ _R T → W que hace conmutar todo el diagrama.

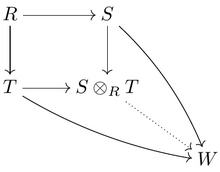
Dadas dos R -álgebras S y T , su producto tensorial

S ⊗ _R T

es nuevamente un R -álgebra conmutativa . En algunos casos, el producto tensorial puede servir para encontrar un T -álgebra que se relaciona con Z como S se relaciona con R. Por ejemplo,

R [ X ] ⊗ _RT = T [ X ] .

Generación finita

Una R -álgebra S se denomina finitamente generada (como álgebra) si hay un número finito de elementos s ₁ , ..., s _n tales que cualquier elemento de s se puede expresar como un polinomio en el s _i . De manera equivalente, S es isomorfo a

R [ T ₁ , ..., T _n ] / I .

Una condición mucho más fuerte es que S se genera finitamente como un R -módulo , lo que significa que cualquier s puede expresarse como una combinación R -lineal de algún conjunto finito s ₁ , ..., s _n .

Anillos locales

Un anillo se llama local si tiene un único ideal máximo, denotado por m . Para cualquier anillo (no necesariamente local) R , la localización

Rp _.

En un ideal primo, p es local. Esta localización refleja las propiedades geométricas de Spec R "alrededor de p ". Varias nociones y problemas del álgebra conmutativa se pueden reducir al caso en que R es local, lo que hace que los anillos locales sean una clase de anillos estudiada en particular. El campo de residuos de R se define como

k = R / m .

Cualquier módulo R M produce un espacio vectorial k dado por M / mM . El lema de Nakayama muestra que este pasaje preserva información importante: un módulo M finitamente generado es cero si y solo si M / mM es cero.

Anillos locales regulares

La curva plana cúbica (roja) definida por la ecuación y ² = x ² ( x + 1 ) es singular en el origen, es decir, el anillo k [ x , y ] / y ² − x ² ( x + 1 ), no es un anillo regular. El cono tangente (azul) es una unión de dos líneas, lo que también refleja la singularidad.

El espacio vectorial k m / m2 es una encarnación algebraica del espacio cotangente . De manera informal, los elementos de m pueden considerarse como funciones que se anulan en el punto ^p , mientras que m2 ^contiene las que se anulan con orden al menos 2. Para cualquier anillo local noetheriano R , la desigualdad

dimensión _k m / m2 ≥ ^dimensión R

es cierto, lo que refleja la idea de que el espacio cotangente (o equivalentemente, la tangente) tiene al menos la dimensión del espacio Spec R . Si la igualdad es cierta en esta estimación, R se llama un anillo local regular . Un anillo local noetheriano es regular si y solo si el anillo (que es el anillo de funciones en el cono tangente ) es isomorfo a un anillo polinomial sobre k . En términos generales, los anillos locales regulares son algo similares a los anillos polinomiales. ^[1] Los anillos locales regulares son UFD. ^[2] $${\displaystyle \bigoplus _{n}m^{n}/m^{n+1}}$$

Los anillos de valoración discretos están equipados con una función que asigna un número entero a cualquier elemento r . Este número, llamado valoración de r, puede considerarse informalmente como un orden cero o polar de r . Los anillos de valoración discretos son precisamente los anillos locales regulares unidimensionales. Por ejemplo, el anillo de gérmenes de funciones holomorfas en una superficie de Riemann es un anillo de valoración discreto.

Intersecciones completas

El cúbico retorcido (verde) es una intersección completa en teoría de conjuntos, pero no una intersección completa.

Según el teorema del ideal principal de Krull , un resultado fundamental en la teoría dimensional de los anillos , la dimensión de

R = k [ T ₁ , ..., T _r ] / ( f ₁ , ..., f _n )

es al menos r − n . Un anillo R se denomina anillo de intersección completo si se puede presentar de forma que alcance este límite mínimo. Esta noción también se estudia principalmente para anillos locales. Cualquier anillo local regular es un anillo de intersección completo, pero no a la inversa.

Un anillo R es una intersección completa en teoría de conjuntos si el anillo reducido asociado a R , es decir, el que se obtiene al dividir todos los elementos nilpotentes, es una intersección completa. A fecha de 2017, se desconoce en general si las curvas en el espacio tridimensional son intersecciones completas en teoría de conjuntos. ^[3]

Anillos Cohen-Macaulay

La profundidad de un anillo local R es el número de elementos en alguna (o, como se puede demostrar, cualquier) secuencia regular máxima, es decir, una secuencia a ₁ , ..., a _n ∈ m tal que todos los a _i son divisores distintos de cero en

R / ( a ₁ , ..., a _{i −1} ).

Para cualquier anillo noetheriano local, la desigualdad

profundidad( R ) ≤ dim( R )

se cumple. Un anillo local en el que tiene lugar la igualdad se llama anillo de Cohen-Macaulay . Los anillos de intersección completa locales y, a fortiori, los anillos locales regulares son de Cohen-Macaulay, pero no a la inversa. Los de Cohen-Macaulay combinan propiedades deseables de los anillos regulares (como la propiedad de ser anillos universalmente catenarios , lo que significa que la (co)dimensión de los primos se comporta bien), pero también son cocientes de ejecución más robustos que los anillos locales regulares. ^[4]

Construyendo anillos conmutativos

Existen varias formas de construir nuevos anillos a partir de otros ya existentes. El objetivo de estas construcciones es a menudo mejorar ciertas propiedades del anillo para que sea más fácil de entender. Por ejemplo, un dominio integral que está integralmente cerrado en su campo de fracciones se denomina normal . Esta es una propiedad deseable, por ejemplo, cualquier anillo unidimensional normal es necesariamente regular . La conversión ^{[ aclaración necesaria ]} de un anillo en normal se conoce como normalización .

Terminaciones

Si I es un ideal en un anillo conmutativo R , las potencias de I forman vecindades topológicas de 0 que permiten que R sea visto como un anillo topológico . Esta topología se llama topología I -ádica . R puede entonces completarse con respecto a esta topología. Formalmente, la completitud I -ádica es el límite inverso de los anillos R / I ⁿ . Por ejemplo, si k es un cuerpo, k [[ X ]], el anillo formal de la serie de potencias en una variable sobre k , es la completitud I -ádica de k [ X ] donde I es el ideal principal generado por X . Este anillo sirve como un análogo algebraico del disco. Análogamente, el anillo de números enteros p -ádicos es la completitud de Z con respecto al ideal principal ( p ). Cualquier anillo que sea isomorfo a su propia completitud, se llama completo .

Los anillos locales completos satisfacen el lema de Hensel , que , en términos generales, permite extender soluciones (de varios problemas) sobre el cuerpo de residuos k hasta R.

Nociones homológicas

Se han estudiado varios aspectos más profundos de los anillos conmutativos utilizando métodos del álgebra homológica . Hochster (2007) enumera algunas preguntas abiertas en esta área de investigación activa.

Módulos proyectivos y funtores Ext

Los módulos proyectivos pueden definirse como los sumandos directos de módulos libres. Si R es local, cualquier módulo proyectivo finitamente generado es en realidad libre, lo que da contenido a una analogía entre módulos proyectivos y fibrados vectoriales . ^[5] El teorema de Quillen-Suslin afirma que cualquier módulo proyectivo finitamente generado sobre k [ T ₁ , ..., T _n ] ( k un cuerpo) es libre, pero en general estos dos conceptos difieren. Un anillo noetheriano local es regular si y solo si su dimensión global es finita, digamos n , lo que significa que cualquier R -módulo finitamente generado tiene una resolución por módulos proyectivos de longitud como máximo n .

La prueba de esta y otras afirmaciones relacionadas se basa en el uso de métodos homológicos, como el funtor Ext . Este funtor es el funtor derivado del funtor

Casa _R ( M , −).

El último funtor es exacto si M es proyectivo, pero no en caso contrario: para una función sobreyectiva E → F de R -módulos, una función M → F no necesita extenderse a una función M → E . Los funtores Ext superiores miden la falta de exactitud del funtor Hom. La importancia de esta construcción estándar en las raíces del álgebra homológica se puede ver a partir del hecho de que un anillo noetheriano local R con cuerpo de residuos k es regular si y solo si

Extensión ⁿ ( k , k )

se desvanece para todos los n suficientemente grandes . Además, las dimensiones de estos grupos Ext, conocidos como números de Betti , crecen polinomialmente en n si y solo si R es un anillo de intersección completo local . ^[6] Un argumento clave en tales consideraciones es el complejo de Koszul , que proporciona una resolución libre explícita del campo de residuos k de un anillo local R en términos de una secuencia regular.

Llanura

El producto tensorial es otro funtor no exacto relevante en el contexto de los anillos conmutativos: para un R -módulo general M , el funtor

M ⊗ _R −

es sólo exactamente exacto. Si es exacto, M se llama plano . Si R es local, cualquier módulo plano finitamente presentado está libre de rango finito, por lo tanto, es proyectivo. A pesar de estar definida en términos de álgebra homológica, la planicidad tiene profundas implicaciones geométricas. Por ejemplo, si una R -álgebra S es plana, las dimensiones de las fibras

S / pS = S ⊗ _R R / p

(para ideales primos p en R ) tienen la dimensión "esperada", es decir, dim S − dim R + dim( R / p ) .

Propiedades

Por el teorema de Wedderburn , todo anillo de división finito es conmutativo y, por lo tanto, un cuerpo finito . Otra condición que asegura la conmutatividad de un anillo, debida a Jacobson , es la siguiente: para cada elemento r de R existe un entero n > 1 tal que r ⁿ = r . ^[7] Si, r ² = r para cada r , el anillo se llama anillo booleano . También se conocen condiciones más generales que garantizan la conmutatividad de un anillo. ^[8]

Generalizaciones

Anillos conmutativos graduados

Un pantalón es un cobordismo entre un círculo y dos círculos disjuntos. Las clases de cobordismo, con el producto cartesiano como multiplicación y la unión disjunta como suma, forman el anillo de cobordismo .

Un anillo graduado R = ⨁ _{i ∊ Z} R _i se llama conmutativo graduado si, para todos los elementos homogéneos a y b ,

ab = (−1) grados ^{a ⋅ grados b} ba .

Si los R _i están conectados por diferenciales ∂ tales que se cumple una forma abstracta de la regla del producto , es decir,

∂( ab ) = ∂( a ) b + (−1) grado ^{a a∂} ( b ),

R se denomina álgebra graduada diferencial conmutativa (cdga). Un ejemplo es el complejo de formas diferenciales en una variedad , con la multiplicación dada por el producto exterior , es una cdga. La cohomología de una cdga es un anillo conmutativo graduado, a veces denominado anillo de cohomología . De esta manera surge una amplia gama de ejemplos de anillos graduados. Por ejemplo, el anillo de Lazard es el anillo de clases de cobordismo de variedades complejas.

Un anillo conmutativo graduado con respecto a una gradación de Z /2 (en oposición a Z ) se llama superálgebra .

Una noción relacionada es un anillo casi conmutativo , lo que significa que R se filtra de tal manera que el anillo graduado asociado

gr R  := ⨁ F _i R / ⨁ F _{i −1} R

es conmutativa. Un ejemplo es el álgebra de Weyl y anillos más generales de operadores diferenciales .

Anillos conmutativos simples

Un anillo conmutativo simplicial es un objeto simplicial de la categoría de anillos conmutativos. Son bloques de construcción para la geometría algebraica derivada (conectiva) . Una noción estrechamente relacionada pero más general es la de E _∞ -ring .

Aplicaciones de los anillos conmutativos

• Funciones holomorfas
• Teoría K algebraica
• Teoría K topológica
• Estructuras de poder divididas
• Vectores de Witt
• Álgebra de Hecke (utilizada en la prueba de Wiles del último teorema de Fermat )
• Los anillos de época de Fontaine
• Álgebra de grupos
• Álgebra de convolución (de un grupo conmutativo)
• Álgebra de Fréchet

Véase también

• Casi anillo , cierta generalización de un anillo conmutativo
• Divisibilidad (teoría de anillos) : elemento nilpotente (p. ej. números duales )
• Ideales y módulos: Radical de un ideal , equivalencia de Morita
• Homomorfismos de anillo : elemento integral : teorema de Cayley-Hamilton , dominio integralmente cerrado , anillo de Krull , teorema de Krull-Akizuki , teorema de Mori-Nagata
• Primos: Lema de evitación de primos , Radical de Jacobson , Radical nil de un anillo , Espectro: Espacio compacto , Anillo conexo , Cálculo diferencial sobre álgebras conmutativas , Teorema de Banach-Stone
• Anillos locales : Anillo local de Gorenstein (también utilizado en la prueba de Wiles del último teorema de Fermat ): Dualidad (matemáticas) , Eben Matlis ; Módulo dualizante , Teorema de Popescu , Teorema de aproximación de Artin .

Notas

1. Esta noción puede relacionarse con el espectro de un operador lineal; véase Espectro de un C*-álgebra y representación de Gelfand .

Citas

1. Matsumura 1989, pág. 143, §7, Observaciones
2. Matsumura 1989, §19, Teorema 48
3. Lyubeznik 1989
4. Eisenbud 1995, Corolario 18.10, Proposición 18.13
5. Véase también el teorema de Serre-Swan
6. Christensen, Striuli y Veliche 2010
7. Jacobson 1945
8. Pinter-Lucke 2007

Referencias

• Christensen, Lars Winther; Striuli, Janet; Veliche, Oana (2010), "Crecimiento en la resolución inyectiva mínima de un anillo local", Journal of the London Mathematical Society , Segunda serie, 81 (1): 24–44, arXiv : 0812.4672 , doi : 10.1112/jlms/jdp058, S2CID  14764965
• Eisenbud, David (1995), Álgebra conmutativa. Con vistas a la geometría algebraica. , Textos de posgrado en matemáticas , vol. 150, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94268-1, Sr.  1322960
• Hochster, Melvin (2007), "Conjeturas homológicas, antiguas y nuevas", Illinois J. Math. , 51 (1): 151–169, doi : 10.1215/ijm/1258735330
• Jacobson, Nathan (1945), "Teoría de la estructura de álgebras algebraicas de grado acotado", Annals of Mathematics , 46 (4): 695–707, doi :10.2307/1969205, ISSN  0003-486X, JSTOR  1969205
• Lyubeznik, Gennady (1989), "Estudio de problemas y resultados sobre el número de ecuaciones definitorias", Representaciones, resoluciones y números entrelazados , pp. 375–390, Zbl  0753.14001
• Matsumura, Hideyuki (1989), Teoría del anillo conmutativo , Cambridge Studies in Advanced Mathematics (2.ª ed.), Cambridge University Press , ISBN 978-0-521-36764-6
• Pinter-Lucke, James (2007), "Condiciones de conmutatividad para anillos: 1950-2005", Expositiones Mathematicae , 25 (2): 165-174, doi : 10.1016/j.exmath.2006.07.001 , ISSN  0723-0869

Lectura adicional

• Atiyah, Michael ; Macdonald, IG (1969), Introducción al álgebra conmutativa , Addison-Wesley Publishing Co.
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Anillos conmutativos noetherianos y de Krull , Ellis Horwood Series: Matemáticas y sus aplicaciones, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimensión, multiplicidad y métodos homológicos , Ellis Horwood Series: Matemáticas y sus aplicaciones., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
• Kaplansky, Irving (1974), Anillos conmutativos (edición revisada), University of Chicago Press , MR  0345945
• Nagata, Masayoshi (1975) [1962], Anillos locales , Interscience Tracts in Pure and Applied Mathematics, vol. 13, Interscience Publishers, págs. xiii+234, ISBN 978-0-88275-228-0, Sr.  0155856
• Zariski, Oscar ; Samuel, Pierre (1958–60), Álgebra conmutativa I, II , Serie universitaria en matemáticas superiores, Princeton, NJ: D. van Nostrand, Inc. (Reimpreso en 1975-76 por Springer como volúmenes 28-29 de Graduate Texts in Mathematics).