Espacio afín

En matemáticas , un espacio afín es una estructura geométrica que generaliza algunas de las propiedades de los espacios euclidianos de tal manera que estos son independientes de los conceptos de distancia y medida de ángulos , conservando sólo las propiedades relacionadas con el paralelismo y la razón de longitudes para los paralelos. segmentos de linea . El espacio afín es el escenario de la geometría afín .

Como en el espacio euclidiano, los objetos fundamentales en un espacio afín se llaman puntos , que pueden considerarse como ubicaciones en el espacio sin ningún tamaño ni forma: de dimensión cero . A través de cualquier par de puntos se puede trazar una línea recta infinita , un conjunto unidimensional de puntos; a través de tres puntos cualesquiera que no sean colineales, se puede dibujar un plano bidimensional ; y en general a través de $k + 1$ puntos en posición general se puede dibujar un subespacio plano o afín $de k$ dimensiones . El espacio afín se caracteriza por una noción de pares de líneas paralelas que se encuentran dentro del mismo plano pero que nunca se encuentran (las líneas no paralelas dentro del mismo plano se cruzan en un punto). Dada cualquier línea, se puede trazar una línea paralela a ella a través de cualquier punto del espacio, y se dice que la clase de equivalencia de líneas paralelas comparte una dirección .

Unlike for vectors in a vector space, in an affine space there is no distinguished point that serves as an origin. There is no predefined concept of adding or multiplying points together, or multiplying a point by a scalar number. However, for any affine space, an associated vector space can be constructed from the differences between start and end points, which are called displacement vectors, translation vectors or simply translations.^[1] Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. While points cannot be arbitrarily added together, it is meaningful to take affine combinations of points: weighted sums with numerical coefficients summing to 1, resulting in another point. These coefficients define a barycentric coordinate system for the flat through the points.

Any vector space may be viewed as an affine space; this amounts to "forgetting" the special role played by the zero vector. In this case, elements of the vector space may be viewed either as points of the affine space or as displacement vectors or translations. When considered as a point, the zero vector is called the origin. Adding a fixed vector to the elements of a linear subspace (vector subspace) of a vector space produces an affine subspace of the vector space. One commonly says that this affine subspace has been obtained by translating (away from the origin) the linear subspace by the translation vector (the vector added to all the elements of the linear space). In finite dimensions, such an affine subspace is the solution set of an inhomogeneous linear system. The displacement vectors for that affine space are the solutions of the corresponding homogeneous linear system, which is a linear subspace. Linear subspaces, in contrast, always contain the origin of the vector space.

The dimension of an affine space is defined as the dimension of the vector space of its translations. An affine space of dimension one is an affine line. An affine space of dimension 2 is an affine plane. An affine subspace of dimension $n - 1$ in an affine space or a vector space of dimension $n$ is an affine hyperplane.

Informal description

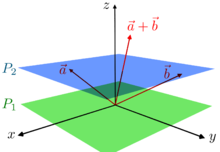
La siguiente caracterización puede ser más fácil de entender que la definición formal habitual: un espacio afín es lo que queda de un espacio vectorial después de haber olvidado qué punto es el origen (o, en palabras del matemático francés Marcel Berger , "un espacio afín el espacio no es más que un espacio vectorial cuyo origen intentamos olvidar, añadiendo traslaciones a las aplicaciones lineales" ^[2] ). Imagine que Alice sabe que cierto punto es el origen real, pero Bob cree que otro punto (llámelo $p)$ es el origen. Se van a sumar dos vectores, $a$ y $b .$ Bob dibuja una flecha desde el punto $p$ hasta el punto $a$ y otra flecha desde el punto $p$ hasta el punto $b$ , y completa el paralelogramo para encontrar lo que Bob cree que es $a + b$ , pero Alice sabe que en realidad ha calculado

p + (una - p) + (segundo - p)

De manera similar, Alice y Bob pueden evaluar cualquier combinación lineal de $a$ y $b$ , o de cualquier conjunto finito de vectores, y generalmente obtendrán respuestas diferentes. Sin embargo, si la suma de los coeficientes en una combinación lineal es 1, entonces Alice y Bob llegarán a la misma respuesta.

Si Alice viaja a

λa + (1 - λ) b

entonces Bob puede viajar de manera similar a

p + λ(a - p) + (1 - λ)(b - p) = λ a + (1 - λ) b

Bajo esta condición, para todos los coeficientes $λ + (1 - λ) = 1$ , Alice y Bob describen el mismo punto con la misma combinación lineal, a pesar de utilizar orígenes diferentes.

Mientras que sólo Alice conoce la "estructura lineal", tanto Alice como Bob conocen la "estructura afín", es decir, los valores de las combinaciones afines , definidas como combinaciones lineales en las que la suma de los coeficientes es 1. Un conjunto con una estructura afín es un espacio afín.

Definición

Si bien el espacio afín se puede definir axiomáticamente (ver § Axiomas a continuación), de manera análoga a la definición de espacio euclidiano implícita en los Elementos de Euclides , por conveniencia, la mayoría de las fuentes modernas definen los espacios afines en términos de la bien desarrollada teoría del espacio vectorial.

Un espacio afín es un conjunto $A$ junto con un espacio vectorial , y una acción transitiva y libre del grupo aditivo de sobre el conjunto $A.$ ^[3] Los elementos del espacio afín $A$ se llaman puntos . Se dice que el espacio vectorial está asociado al espacio afín, y sus elementos se denominan vectores , traslaciones o, a veces, vectores libres . ${\overrightarrow {A}}$ ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

Explícitamente, la definición anterior significa que la acción es una asignación, generalmente denotada como una adición,

{\begin{aligned}A\times {\overrightarrow {A}}&\to A\\(a,v)\;&\mapsto a+v,\end{aligned}}

que tiene las siguientes propiedades. ^[4]^[5]^[6]

Identidad correcta :
$\forall a\in A,\;a+0=a$ , donde $0$ es el vector cero en ${\overrightarrow {A}}$
Asociatividad :
$\forall v,w\in {\overrightarrow {A}},\forall a\in A,\;(a+v)+w=a+(v+w)$ (aquí el último $+$ es la suma en ) ${\overrightarrow {A}}$
Acción libre y transitiva :
Para cada uno , el mapeo es una biyección . $a\in A$ ${\overrightarrow {A}}\to A\colon v\mapsto a+v$

Las dos primeras propiedades son simplemente propiedades definitorias de una acción de grupo (derecha). La tercera propiedad caracteriza las acciones libres y transitivas, el carácter onto proviene de la transitividad, y luego el carácter inyectivo se deriva de que la acción es libre. Hay una cuarta propiedad que se desprende de 1, 2 anteriores:

Existencia de traducciones uno a uno

Para todos , el mapeo es una biyección.

v\in {\overrightarrow {A}}

A\to A\colon a\mapsto a+v

La propiedad 3 se utiliza a menudo en la siguiente forma equivalente (la quinta propiedad).

Sustracción:

Para cada

a, b

A

, existe un único , denotado

b

-

a

, tal que .

v\in {\overrightarrow {A}}

b=a+v

Otra forma de expresar la definición es que un espacio afín es un espacio principal homogéneo para la acción del grupo aditivo de un espacio vectorial. Los espacios homogéneos están, por definición, dotados de una acción grupal transitiva, y para un espacio homogéneo principal dicha acción transitiva es, por definición, libre.

Resta y axiomas de Weyl

Las propiedades de la acción grupal permiten la definición de resta para cualquier par ordenado $(b, a)$ de puntos en $A$ , produciendo un vector de . Este vector, denotado o , se define como el vector único de tal manera que ${\overrightarrow {A}}$ $b-a$ ${\overrightarrow {ab}}$ ${\overrightarrow {A}}$

a+(b-a)=b.

La existencia se deriva de la transitividad de la acción, y la unicidad se deriva de que la acción es libre.

Esta resta tiene las dos propiedades siguientes, llamadas axiomas de Weyl : ^[7]

$\forall a\in A,\;\forall v\in {\overrightarrow {A}}$ , hay un punto único tal que $b\in A$ $b-a=v.$
$\forall a,b,c\in A,\;(c-b)+(b-a)=c-a.$

La propiedad del paralelogramo se cumple en espacios afines, donde se expresa como: dados cuatro puntos las igualdades y son equivalentes. Esto resulta del segundo axioma de Weyl, ya que $a,b,c,d,$ $b-a=d-c$ $c-a=d-b$ $d-a=(d-b)+(b-a)=(d-c)+(c-a).$

Los espacios afines se pueden definir de manera equivalente como un conjunto de puntos $A$ , junto con un espacio vectorial y una resta que satisfaga los axiomas de Weyl. En este caso, la suma de un vector a un punto se define a partir del primero de los axiomas de Weyl. ${\overrightarrow {A}}$

Subespacios afines y paralelismo.

Un subespacio afín (también llamado, en algunos contextos, variedad lineal , plano o, sobre los números reales , variedad lineal ) $B$ de un espacio afín $A$ es un subconjunto de $A$ tal que, dado un punto , el conjunto de vectores es un subespacio lineal de . Esta propiedad, que no depende de la elección de $a$ , implica que $B$ es un espacio afín, que tiene como espacio vectorial asociado. $a\in B$ ${\overrightarrow {B}}=\{b-a\mid b\in B\}$ ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

Los subespacios afines de $A$ son los subconjuntos de $A$ de la forma

a+V=\{a+w:w\in V\},

donde $a$ es un punto de $A$ y $V$ un subespacio lineal de . ${\overrightarrow {A}}$

El subespacio lineal asociado con un subespacio afín a menudo se denomina sudirección , y se dice que dos subespacios que comparten la misma dirección sonparalelos.

Esto implica la siguiente generalización del axioma de Playfair : Dada una dirección $V$ , para cualquier punto $a$ de $A$ existe uno y sólo un subespacio afín de dirección $V$ , que pasa por $a$ , es decir, el subespacio $a + V.$

Cada traducción asigna cualquier subespacio afín a un subespacio paralelo. $A\to A:a\mapsto a+v$

El término paralelo también se utiliza para dos subespacios afines de modo que la dirección de uno está incluida en la dirección del otro.

mapa afín

Dados dos espacios afines $A$ y $B$ cuyos espacios vectoriales asociados son y , un mapa afín o homomorfismo afín de $A$ a $B$ es un mapa ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

f:A\to B

tal que

{\begin{aligned}{\overrightarrow {f}}:{\overrightarrow {A}}&\to {\overrightarrow {B}}\\b-a&\mapsto f(b)-f(a)\end{aligned}}

es un mapa lineal bien definido . Por estar bien definido se quiere decir que $b$ $-$ $a$ $=$ $d$ $-$ $c$ implica $f$ $($ $b$ $) -$ $f$ $($ $a$ $) =$ $f$ $($ $d$ $) -$ $f$ $($ $c$ $)$ . $f$

Esto implica que, para un punto y un vector , se tiene $a\in A$ $v\in {\overrightarrow {A}}$

f(a+v)=f(a)+{\overrightarrow {f}}(v).

Por lo tanto, dado que para cualquier $b$ dado en $A$ , $b = a + v$ $para un v$ único , $f$ está completamente definida por su valor en un solo punto y el mapa lineal asociado . ${\overrightarrow {f}}$

Endomorfismos

Una transformación afín o endomorfismo de un espacio afín es un mapa afín de ese espacio a sí mismo. Una familia importante de ejemplos son las traducciones: dado un vector , el mapa de traducción que envía cada entrada es un mapa afín. Otra familia importante de ejemplos son los mapas lineales centrados en un origen: dado un punto y un mapa lineal , se puede definir un mapa afín por $A$ ${\overrightarrow {v}}$ $T_{\overrightarrow {v}}:A\rightarrow A$ $a\mapsto a+{\overrightarrow {v}}$ $a$ $A$ $b$ $M$ $L_{M,b}:A\rightarrow A$

L_{M,b}(a)=b+M(a-b)

a

A

Después de elegir el origen , cualquier mapa afín se puede escribir de forma única como una combinación de una traducción y un mapa lineal centrado en . $b$ $b$

Espacios vectoriales como espacios afines

Todo espacio vectorial $V$ puede considerarse como un espacio afín sobre sí mismo. Esto significa que cada elemento de $V$ puede considerarse como un punto o como un vector. Este espacio afín a veces se denota $(V, V)$ para enfatizar el doble papel de los elementos de $V.$ Cuando se considera como un punto, el vector cero comúnmente se denota $como o$ (u $O$ , cuando se usan letras mayúsculas para los puntos) y se llama origen .

Si $A$ es otro espacio afín sobre el mismo espacio vectorial (es decir ), la elección de cualquier punto $a$ en $A$ define un isomorfismo afín único, que es la identidad de $V$ y asigna $a$ a $o$ . En otras palabras, la elección de un origen $a$ en $A$ nos permite identificar $A$ y $($ $V$ $,$ $V$ $)$ hasta un isomorfismo canónico . La contraparte de esta propiedad es que el espacio afín $A$ puede identificarse con el espacio vectorial $V$ en el que "se ha olvidado el lugar del origen". $V={\overrightarrow {A}}$

Relación con los espacios euclidianos

Definición de espacios euclidianos

Los espacios euclidianos (incluida la línea unidimensional, el plano bidimensional y el espacio tridimensional comúnmente estudiados en geometría elemental, así como sus análogos de dimensiones superiores) son espacios afines.

De hecho, en la mayoría de las definiciones modernas, un espacio euclidiano se define como un espacio afín, de modo que el espacio vectorial asociado es un espacio producto interno real de dimensión finita, es decir, un espacio vectorial sobre los reales con una forma cuadrática definida positiva $q. (X)$ . El producto interno de dos vectores $xey$ es el valor de la forma $bilineal$ simétrica

x\cdot y={\frac {1}{2}}(q(x+y)-q(x)-q(y)).

La distancia euclidiana habitual entre dos puntos $A$ y $B$ es

d(A,B)={\sqrt {q(B-A)}}.

En una definición anterior de espacios euclidianos a través de geometría sintética , los vectores se definen como clases de equivalencia de pares ordenados de puntos bajo equipolencia (los pares $(A, B)$ y $(C, D)$ son equipolentes si los puntos $A, B, D, C$ ( en este orden) forman un paralelogramo ). Es sencillo verificar que los vectores forman un espacio vectorial, que el cuadrado de la distancia euclidiana es una forma cuadrática en el espacio de vectores y que las dos definiciones de espacios euclidianos son equivalentes.

Propiedades afines

En geometría euclidiana , la frase común " propiedad afín " se refiere a una propiedad que se puede demostrar en espacios afines, es decir, que se puede demostrar sin utilizar la forma cuadrática y su producto interno asociado. En otras palabras, una propiedad afín es una propiedad que no involucra longitudes ni ángulos. Ejemplos típicos son el paralelismo y la definición de tangente . Un no ejemplo es la definición de normal .

De manera equivalente, una propiedad afín es una propiedad que es invariante bajo transformaciones afines del espacio euclidiano.

Combinaciones afines y baricentro.

Sea $a 1, ..., an una$ colección de $n$ puntos en un espacio afín y sean $n$ elementos del campo terrestre . $\lambda _{1},\dots ,\lambda _{n}$

Suponer que . Para dos puntos cualesquiera $o$ y $o'$ se tiene $\lambda _{1}+\dots +\lambda _{n}=0$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}=\lambda _{1}{\overrightarrow {o'a_{1}}}+\dots +\lambda _{n}{\overrightarrow {o'a_{n}}}.

Por tanto, esta suma es independiente de la elección del origen, y el vector resultante puede denotarse

\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

Cuando , se recupera la definición de la resta de puntos. $n=2,\lambda _{1}=1,\lambda _{2}=-1$

Ahora supongamos que los elementos del campo satisfacen . Para alguna elección de origen $o$ , denote por el punto único tal que $\lambda _{1}+\dots +\lambda _{n}=1$ $g$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}={\overrightarrow {og}}.

Se puede demostrar que es independiente de la elección de $o$ . Por lo tanto, si $g$

\lambda _{1}+\dots +\lambda _{n}=1,

uno puede escribir

g=\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

El punto se llama baricentro de las pesas . Se dice también que es una combinación afín de los coeficientes with . $g$ $a_{i}$ $\lambda _{i}$ $g$ $a_{i}$ $\lambda _{i}$

Ejemplos

Cuando los niños encuentran las respuestas a sumas como $4 + 3$ o $4 - 2$ contando hacia la derecha o hacia la izquierda en una recta numérica , están tratando la recta numérica como un espacio afín unidimensional.
El espacio de energías es un espacio afín para , ya que muchas veces no tiene sentido hablar de energía absoluta, pero sí lo es hablar de diferencias de energía. La energía del vacío , cuando se define, señala un origen canónico. $\mathbb {R}$
El espacio físico a menudo se modela como un espacio afín en entornos no relativistas y en entornos relativistas. Para distinguirlos del espacio vectorial, a veces se les llama espacios euclidianos y . $\mathbb {R} ^{3}$ $\mathbb {R} ^{1,3}$ ${\text{E}}(3)$ ${\text{E}}(1,3)$
Cualquier clase lateral de un subespacio $V$ de un espacio vectorial es un espacio afín sobre ese subespacio.
Si $T$ es una matriz y $b$ se encuentra en su espacio columna , el conjunto de soluciones de la ecuación $T x = b$ es un espacio afín sobre el subespacio de soluciones de $T x = 0$ .
Las soluciones de una ecuación diferencial lineal no homogénea forman un espacio afín sobre las soluciones de la ecuación lineal homogénea correspondiente.
Generalizando todo lo anterior, si $T : V \to W$ es una aplicación lineal e $y$ está en su imagen , el conjunto de soluciones $x \in V$ de la ecuación $T x = y$ es una clase lateral del núcleo de $T$ y, por tanto, es una espacio afín sobre $Ker T$ .
El espacio de subespacios complementarios (lineales) de un subespacio vectorial $V$ en un espacio vectorial $W$ es un espacio afín, sobre $Hom(W / V, V)$ . Es decir, si $0 \to V \to W \to X \to 0$ es una secuencia corta y exacta de espacios vectoriales, entonces el espacio de todas las divisiones de la secuencia exacta lleva naturalmente la estructura de un espacio afín sobre $Hom(X, V)$ .
El espacio de conexiones (visto desde el paquete de vectores , donde es una variedad suave ) es un espacio afín para el espacio vectorial de 1-formas valoradas . El espacio de conexiones (visto desde el paquete principal ) es un espacio afín para el espacio vectorial de formas 1 con valor, donde está el paquete adjunto asociado . $E\xrightarrow {\pi } M$ $M$ ${\text{End}}(E)$ $P\xrightarrow {\pi } M$ ${\text{ad}}(P)$ ${\text{ad}}(P)$

Lapso y bases afines

$Para cualquier subconjunto X$ no vacío de un espacio afín $A$ , existe un subespacio afín más pequeño que lo contiene, llamado intervalo afín de $X$ . Es la intersección de todos los subespacios afines que contienen X $y$ su dirección es la intersección de las direcciones de los subespacios afines que contienen $X.$

El tramo afín de X $es$ el conjunto de todas las combinaciones afines (finitas) de puntos de $X$ , y su dirección es el tramo lineal de $x - y$ para $x$ e $y$ en $X.$ Si uno elige un punto particular x $0,$ la dirección del tramo afín de $X$ es también el tramo lineal de $x - x 0$ para $x$ en $X.$

Se dice también que el tramo afín de $X$ es generado por $X$ y que $X$ es un conjunto generador de su tramo afín.

Se dice que un conjunto $X de puntos de un espacio afín es$ afínmente independiente o, simplemente,independiente, si el intervalo afín de cualquiersubconjunto estrictode $X$ es un subconjunto estricto del intervalo afínde $X.$ UnLa base afín omarco baricéntrico(ver § Coordenadas baricéntricas, más abajo) de un espacio afín es un conjunto generador que también es independiente (es decir, unconjunto generador mínimo).

Recuerde que la dimensión de un espacio afín es la dimensión de su espacio vectorial asociado. Las bases de un espacio afín de dimensión finita $n$ son los subconjuntos independientes de $n + 1$ elementos o, de manera equivalente, los subconjuntos generadores de $n + 1$ elementos. De manera equivalente, ${x 0, ..., x n$ } es una base afín de un espacio afín si y sólo si ${x 1 - x 0, ..., x n - x 0$ } es una base lineal del vector asociado espacio.

Coordenadas

Hay dos tipos de sistemas de coordenadas fuertemente relacionados que pueden definirse en espacios afines.

Coordenadas baricéntricas

Sea $A$ un espacio afín de dimensión $n$ sobre un campo k $y$ sea una base afín de $A.$ Las propiedades de una base afín implican que para cada $x$ en $A$ hay una única $($ $n$ $+ 1)$ - tupla de elementos de $k$ tal que $\{x_{0},\dots ,x_{n}\}$ $(\lambda _{0},\dots ,\lambda _{n})$

\lambda _{0}+\dots +\lambda _{n}=1

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

Se denominan coordenadas baricéntricas de $x$ sobre la base afín . Si los $x$ $i$ se consideran cuerpos que tienen pesos (o masas) , el punto $x$ es, por tanto, el baricentro del $x$ $i$ , y esto explica el origen del término coordenadas baricéntricas . $\lambda _{i}$ $\{x_{0},\dots ,x_{n}\}$ $\lambda _{i}$

Las coordenadas baricéntricas definen un isomorfismo afín entre el espacio afín $A$ y el subespacio afín de $k n + 1$ definido por la ecuación . $\lambda _{0}+\dots +\lambda _{n}=1$

Para espacios afines de dimensión infinita, se aplica la misma definición, utilizando sólo sumas finitas. Esto significa que para cada punto, sólo un número finito de coordenadas son distintas de cero.

Coordenadas afines

Un marco afín de un espacio afín consta de un punto, llamado origen , y una base lineal del espacio vectorial asociado. Más precisamente, para un espacio afín $A$ con espacio vectorial asociado , el origen $o$ pertenece a $A$ , y la base lineal es una base $($ $v$ $1$ $, ...,$ $v$ $n$ $)$ de (para simplificar la notación, consideramos sólo el caso de dimensión finita, el caso general es similar). ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

Para cada punto $p$ de $A$ , existe una secuencia única de elementos del campo terrestre tal que $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

o equivalente

{\overrightarrow {op}}=\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n}.

Se denominan coordenadas afines de $p$ sobre el marco afín $($ $o$ $,$ $v$ $1$ $, ...,$ $v$ $n$ $)$ . $\lambda _{i}$

Ejemplo: en geometría euclidiana , las coordenadas cartesianas son coordenadas afines relativas a un marco ortonormal , es decir, un marco afín $(o, v 1, ..., v n)$ tal que $(v 1, ..., v n)$ es un base ortonormal .

Relación entre coordenadas baricéntricas y afines

Las coordenadas baricéntricas y las coordenadas afines están fuertemente relacionadas y pueden considerarse equivalentes.

De hecho, dado un marco baricéntrico

(x_{0},\dots ,x_{n}),

se deduce inmediatamente el marco afín

(x_{0},{\overrightarrow {x_{0}x_{1}}},\dots ,{\overrightarrow {x_{0}x_{n}}})=\left(x_{0},x_{1}-x_{0},\dots ,x_{n}-x_{0}\right),

y si

\left(\lambda _{0},\lambda _{1},\dots ,\lambda _{n}\right)

son las coordenadas baricéntricas de un punto sobre el marco baricéntrico, entonces las coordenadas afines del mismo punto sobre el marco afín son

\left(\lambda _{1},\dots ,\lambda _{n}\right).

Por el contrario, si

\left(o,v_{1},\dots ,v_{n}\right)

es un marco afín, entonces

\left(o,o+v_{1},\dots ,o+v_{n}\right)

es un marco baricéntrico. Si

\left(\lambda _{1},\dots ,\lambda _{n}\right)

son las coordenadas afines de un punto sobre el marco afín, entonces sus coordenadas baricéntricas sobre el marco baricéntrico son

\left(1-\lambda _{1}-\dots -\lambda _{n},\lambda _{1},\dots ,\lambda _{n}\right).

Por tanto, las coordenadas baricéntricas y afines son casi equivalentes. En la mayoría de las aplicaciones, se prefieren las coordenadas afines, ya que involucran menos coordenadas que sean independientes. Sin embargo, en situaciones donde los puntos importantes del problema estudiado son afínmente independientes, las coordenadas baricéntricas pueden conducir a un cálculo más simple, como en el siguiente ejemplo.

Ejemplo del triangulo

Los vértices de un triángulo no plano forman una base afín del plano euclidiano . Las coordenadas baricéntricas permiten una fácil caracterización de los elementos del triángulo que no involucran ángulos ni distancias:

Los vértices son los puntos de coordenadas baricéntricas $(1, 0, 0)$ , $(0, 1, 0)$ y $(0, 0, 1)$ . Las líneas que sostienen las aristas son los puntos que tienen coordenada cero. Las aristas mismas son los puntos que tienen una coordenada cero y dos coordenadas no negativas. El interior del triángulo son los puntos cuyas coordenadas son todas positivas. Las medianas son los puntos que tienen dos coordenadas iguales, y el centroide es el punto de coordenadas $(.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/3,1/3,1/3)$ .

Cambio de coordenadas

Caso de coordenadas baricéntricas

Las coordenadas baricéntricas se cambian fácilmente de una base a otra. Sean y bases afines de $A$ . Para cada $x$ en $A$ hay alguna tupla para la cual $\{x_{0},\dots ,x_{n}\}$ $\{x'_{0},\dots ,x'_{n}\}$ $\{\lambda _{0},\dots ,\lambda _{n}\}$

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

De manera similar, para cada uno de la primera base, tenemos en la segunda base $x_{i}\in \{x_{0},\dots ,x_{n}\}$

x_{i}=\lambda _{i,0}x'_{0}+\dots +\lambda _{i,j}x'_{j}+\dots +\lambda _{i,n}x'_{n}

para alguna tupla . Ahora podemos reescribir nuestra expresión en la primera base como una en la segunda con $\{\lambda _{i,0},\dots ,\lambda _{i,n}\}$

\,x=\sum _{i=0}^{n}\lambda _{i}x_{i}=\sum _{i=0}^{n}\lambda _{i}\sum _{j=0}^{n}\lambda _{i,j}x'_{j}=\sum _{j=0}^{n}{\biggl (}\sum _{i=0}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}x'_{j}\,,

dándonos coordenadas en la segunda base como la tupla . ${\textstyle {\bigl \{}\sum _{i}\lambda _{i}\lambda _{i,0},\,\dots ,\,{}}$ ${\textstyle \sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$

Caso de coordenadas afines

Las coordenadas afines también se cambian fácilmente de una base a otra. Sean , y , marcos afines de $A$ . Para cada punto $p$ de $A$ , existe una secuencia única de elementos del campo terrestre tal que $o$ $\{v_{1},\dots ,v_{n}\}$ $o'$ $\{v'_{1},\dots ,v'_{n}\}$ $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

y de manera similar, para cada uno de la primera base, ahora tenemos en la segunda base $v_{i}\in \{v_{1},\dots ,v_{n}\}$

o=o'+\lambda _{o,1}v'_{1}+\dots +\lambda _{o,j}v'_{j}+\dots +\lambda _{o,n}v'_{n}\,

v_{i}=\lambda _{i,1}v'_{1}+\dots +\lambda _{i,j}v'_{j}+\dots +\lambda _{i,n}v'_{n}

para tupla y tuplas . Ahora podemos reescribir nuestra expresión en la primera base como una en la segunda con $\{\lambda _{o,1},\dots ,\lambda _{o,n}\}$ $\{\lambda _{i,1},\dots ,\lambda _{i,n}\}$

{\begin{aligned}\,p&=o+\sum _{i=1}^{n}\lambda _{i}v_{i}={\biggl (}o'+\sum _{j=1}^{n}\lambda _{o,j}v'_{j}{\biggr )}+\sum _{i=1}^{n}\lambda _{i}\sum _{j=1}^{n}\lambda _{i,j}v'_{j}\\&=o'+\sum _{j=1}^{n}{\biggl (}\lambda _{o,j}+\sum _{i=1}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}v'_{j}\,,\end{aligned}}

dándonos coordenadas en la segunda base como la tupla . ${\textstyle {\bigl \{}\lambda _{o,1}+\sum _{i}\lambda _{i}\lambda _{i,1},\,\dots ,\,{}}$ ${\textstyle \lambda _{o,n}+\sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$

Propiedades de los homomorfismos afines.

Representación matricial

Imagen y fibras

Dejar

f\colon E\to F

ser un homomorfismo afín, con

{\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}

su mapa lineal asociado. La imagen de $f$ es el subespacio afín de $F$ , que tiene como espacio vectorial asociado. Como un espacio afín no tiene un elemento cero , un homomorfismo afín no tiene núcleo . Sin embargo, el mapa lineal sí lo hace, y si lo denotamos por su núcleo, entonces para cualquier punto $x$ de , la imagen inversa de $x$ es un subespacio afín de $E$ cuya dirección es . Este subespacio afín se llama fibra de $x$ . $f(E)=\{f(a)\mid a\in E\}$ ${\overrightarrow {f}}({\overrightarrow {E}})$ ${\overrightarrow {f}}$ $K=\{v\in {\overrightarrow {E}}\mid {\overrightarrow {f}}(v)=0\}$ $f(E)$ $f^{-1}(x)$ $K$

Proyección

Un ejemplo importante es la proyección paralela a alguna dirección sobre un subespacio afín. La importancia de este ejemplo radica en que los espacios euclidianos son espacios afines, y que este tipo de proyecciones son fundamentales en la geometría euclidiana .

Más precisamente, dado un espacio afín $E$ con espacio vectorial asociado , sea $F$ un subespacio afín de dirección y $D$ sea un subespacio complementario de in (esto significa que cada vector de puede descomponerse de una manera única como la suma de un elemento de y un elemento de $D$ ). Para cada punto $x$ de $E$ , su proyección a $F$ paralela a $D$ es el único punto $p$ $($ $x$ $)$ en $F$ tal que ${\overrightarrow {E}}$ ${\overrightarrow {F}}$ ${\overrightarrow {F}}$ ${\overrightarrow {E}}$ ${\overrightarrow {E}}$ ${\overrightarrow {F}}$

p(x)-x\in D.

Este es un homomorfismo afín cuyo mapa lineal asociado está definido por ${\overrightarrow {p}}$

{\overrightarrow {p}}(x-y)=p(x)-p(y),

para $x$ e $y$ en $mi$ .

La imagen de esta proyección es $F$ , y sus fibras son los subespacios de dirección $D.$

Espacio cociente

Aunque los núcleos no están definidos para espacios afines, sí lo están los espacios cocientes . Esto resulta del hecho de que "pertenecer a la misma fibra de un homomorfismo afín" es una relación de equivalencia.

Sea $E$ un espacio afín y $D$ un subespacio lineal del espacio vectorial asociado . El cociente $E$ $/$ $D$ de $E$ por $D$ es el cociente de $E$ por la relación de equivalencia tal que $x$ e $y$ son equivalentes si ${\overrightarrow {E}}$

x-y\in D.

Este cociente es un espacio afín, que tiene como espacio vectorial asociado. ${\overrightarrow {E}}/D$

Para cada homomorfismo afín , la imagen es isomorfa al cociente de $E$ por el núcleo del mapa lineal asociado. Este es el primer teorema de isomorfismo para espacios afines. $E\to F$

Axiomas

Los espacios afines suelen estudiarse mediante geometría analítica utilizando coordenadas o, de manera equivalente, espacios vectoriales. También se pueden estudiar como geometría sintética escribiendo axiomas, aunque este enfoque es mucho menos común. Existen varios sistemas diferentes de axiomas para el espacio afín.

Coxeter (1969, p. 192) axioma el caso especial de la geometría afín sobre los reales como geometría ordenada junto con una forma afín del teorema de Desargues y un axioma que establece que en un plano hay como máximo una línea que pasa por un punto dado y que no se encuentra con un línea dada.

Los planos afines satisfacen los siguientes axiomas (Cameron 1991, capítulo 2): (en el que dos rectas se llaman paralelas si son iguales o disjuntas):

Dos puntos distintos cualesquiera se encuentran en una línea única.
Dados un punto y una recta existe una única recta que contiene el punto y es paralela a la recta
Existen tres puntos no colineales.

Además de planos afines sobre campos (o anillos de división ), también existen muchos planos no desarguesianos que satisfacen estos axiomas. (Cameron 1991, capítulo 3) proporciona axiomas para espacios afines de dimensiones superiores.

La geometría afín puramente axiomática es más general que los espacios afines y se trata en un artículo aparte .

Relación con los espacios proyectivos

Los espacios afines están contenidos en espacios proyectivos . Por ejemplo, se puede obtener un plano afín a partir de cualquier plano proyectivo eliminando una línea y todos los puntos de ella y, a la inversa, cualquier plano afín se puede usar para construir un plano proyectivo como cierre agregando una línea en el infinito cuyos puntos corresponden a clases de equivalencia de rectas paralelas . Construcciones similares se mantienen en dimensiones superiores.

Además, las transformaciones del espacio proyectivo que preservan el espacio afín (de manera equivalente, que dejan el hiperplano en el infinito invariante como un conjunto ) producen transformaciones del espacio afín. Por el contrario, cualquier transformación lineal afín se extiende únicamente a una transformación lineal proyectiva , por lo que el grupo afín es un subgrupo del grupo proyectivo . Por ejemplo, las transformaciones de Möbius (transformaciones de la línea proyectiva compleja , o esfera de Riemann ) son afines (transformaciones del plano complejo ) si y sólo si fijan el punto en el infinito .

Geometría algebraica afín

En geometría algebraica , una variedad afín (o, más generalmente, un conjunto algebraico afín ) se define como el subconjunto de un espacio afín que es el conjunto de los ceros comunes de un conjunto de las llamadas funciones polinómicas sobre el espacio afín . Para definir una función polinómica sobre el espacio afín , hay que elegir un marco afín . Entonces, una función polinómica es una función tal que la imagen de cualquier punto es el valor de alguna función polinómica multivariada de las coordenadas del punto. Como un cambio de coordenadas afines puede expresarse mediante funciones lineales (más precisamente funciones afines) de las coordenadas, esta definición es independiente de una elección particular de coordenadas.

La elección de un sistema de coordenadas afines para un espacio afín de dimensión $n$ sobre un campo $k$ induce un isomorfismo afín entre y el espacio de coordenadas afines $k$ $n$ . Esto explica por qué, para simplificar, muchos libros de texto escriben e introducen variedades algebraicas afines como los ceros comunes de funciones polinomiales sobre $k$ $n$ . ^[8] $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}=k^{n}$

Como todo el espacio afín es el conjunto de los ceros comunes del polinomio cero , los espacios afines son variedades algebraicas afines.

Anillo de funciones polinomiales

Según la definición anterior, la elección de un marco afín de un espacio afín permite identificar las funciones polinomiales con polinomios en $n$ variables, representando la i -ésima variable la función que asigna un punto a su $i-$ ésima coordenada. De ello se deduce que el conjunto de funciones polinomiales es una k -álgebra , denotada , que es isomorfa al anillo polinómico . $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $k\left[\mathbb {A} _{k}^{n}\right]$ $k\left[X_{1},\dots ,X_{n}\right]$

Cuando uno cambia de coordenadas, el isomorfismo entre y cambia en consecuencia, y esto induce un automorfismo de , que asigna cada indeterminado a un polinomio de grado uno. De ello se deduce que el grado total define una filtración de , que es independiente de la elección de las coordenadas. El grado total también define una graduación , pero depende de la elección de las coordenadas, ya que un cambio de coordenadas afines puede representar indeterminados en polinomios no homogéneos . $k\left[\mathbb {A} _{k}^{n}\right]$ $k[X_{1},\dots ,X_{n}]$ $k\left[X_{1},\dots ,X_{n}\right]$ $k\left[\mathbb {A} _{k}^{n}\right]$

Topología de Zariski

Los espacios afines sobre campos topológicos , como los números reales o los complejos, tienen una topología natural . La topología de Zariski, que se define para espacios afines en cualquier campo, permite el uso de métodos topológicos en cualquier caso. La topología de Zariski es la topología única en un espacio afín cuyos conjuntos cerrados son conjuntos algebraicos afines (es decir, conjuntos de ceros comunes de funciones polinomiales sobre el conjunto afín). Como, en un campo topológico, las funciones polinómicas son continuas, todo conjunto cerrado de Zariski está cerrado para la topología habitual, si la hay. En otras palabras, en un campo topológico, la topología de Zariski es más burda que la topología natural.

Hay una función inyectiva natural de un espacio afín en el conjunto de ideales primos (es decir, el espectro ) de su anillo de funciones polinomiales. Cuando se han elegido coordenadas afines, esta función asigna el punto de coordenadas al ideal máximo . Esta función es un homeomorfismo (para la topología de Zariski del espacio afín y del espectro del anillo de funciones polinomiales) del espacio afín sobre la imagen de la función. $\left(a_{1},\dots ,a_{n}\right)$ $\left\langle X_{1}-a_{1},\dots ,X_{n}-a_{n}\right\rangle$

El caso de un campo fundamental algebraicamente cerrado es especialmente importante en geometría algebraica, porque, en este caso, el homeomorfismo anterior es un mapa entre el espacio afín y el conjunto de todos los ideales máximos del anillo de funciones (este es el Nullstellensatz de Hilbert ).

Ésta es la idea de partida de la teoría de esquemas de Grothendieck , que consiste, para el estudio de variedades algebraicas, en considerar como "puntos", no sólo los puntos del espacio afín, sino también todos los ideales primos del espectro. Esto permite pegar variedades algebraicas de manera similar a como, para las variedades , los gráficos se pegan entre sí para construir una variedad.

Cohomología

Como todas las variedades afines, los datos locales en un espacio afín siempre se pueden unir globalmente: la cohomología del espacio afín es trivial. Más precisamente, para todas las gavillas coherentes F y números enteros . Esta propiedad también la disfrutan todas las demás variedades afines . Pero también todos los grupos de cohomología étale en espacio afín son triviales. En particular, cada paquete de líneas es trivial. De manera más general, el teorema de Quillen-Suslin implica que todo paquete de vectores algebraicos en un espacio afín es trivial. $H^{i}\left(\mathbb {A} _{k}^{n},\mathbf {F} \right)=0$ $i>0$

Ver también

Casco afín : el subespacio afín más pequeño que contiene un subconjunto
Espacio afín complejo : espacio afín sobre números complejos
Espacio afín exótico : espacio afín real de dimensión par que no es isomorfo a un espacio afín complejo
Espacio (matemáticas) : conjunto matemático con alguna estructura adicional
Sistema de coordenadas baricéntrico

Notas

^ Generalmente se prefiere la palabra traducción a vector de desplazamiento , lo que puede resultar confuso, ya que los desplazamientos también incluyen rotaciones .
^ Berger 1987, pág. 32
^ Berger, Marcel (1984), "Espacios afines", Problemas de geometría , Springer, p. 11, ISBN 9780387909714
^ Berger 1987, pág. 33
^ Pargo, Ernst; Troyer, Robert J. (1989), Geometría afín métrica , pág. 6
^ Tarrida, Agusti R. (2011), "Espacios afines", mapas afines, movimientos euclidianos y cuádricas, Springer, págs. 1-2, ISBN 9780857297105
^ Nomizu y Sasaki 1994, pág. 7
^ Hartshorne 1977, cap. Yo, § 1.

Referencias

Berger, Marcel (1984), "Espacios afines", Problemas de geometría , Springer-Verlag, ISBN 978-0-387-90971-4
Berger, Marcel (1987), Geometría I , Berlín: Springer, ISBN 3-540-11658-3
Cameron, Peter J. (1991), Espacios proyectivos y polares, QMW Maths Notes, vol. 13, Londres: Escuela de Ciencias Matemáticas Queen Mary and Westfield College, MR 1153019
Coxeter, Harold Scott MacDonald (1969), Introducción a la geometría (2ª ed.), Nueva York: John Wiley & Sons , ISBN 978-0-471-50458-0, señor 0123930
Dolgachev, IV ; Shirokov, AP (2001) [1994], "Affine space", Enciclopedia de Matemáticas , EMS Press
Hartshorne, Robin (1977). Geometría Algebraica . Springer-Verlag . ISBN 978-0-387-90244-9. Zbl 0367.14001.
Nomizu, K .; Sasaki, S. (1994), Geometría diferencial afín (nueva ed.), Cambridge University Press, ISBN 978-0-521-44177-3
Pargo, Ernst ; Troyer, Robert J. (1989), Metric Affine Geometry (edición de Dover, publicada por primera vez en 1989), Dover Publications, ISBN 0-486-66108-3
Reventós Tarrida, Agustí (2011), "Espacios afines", Mapas afines, movimientos euclidianos y cuadricas, Springer, ISBN 978-0-85729-709-9