Saul Aaron Kripke ( / ˈkrɪpki / ; 13 de noviembre de 1940 - 15 de septiembre de 2022 ) fue un filósofo analítico y lógico estadounidense . Fue profesor distinguido de Filosofía en el Centro de Graduados de la City University de Nueva York y profesor emérito de la Universidad de Princeton . Desde la década de 1960, ha sido una figura central en varios campos relacionados con la lógica matemática y modal , la filosofía del lenguaje y las matemáticas , la metafísica , la epistemología y la teoría de la recursión .
Kripke realizó contribuciones influyentes y originales a la lógica , especialmente a la lógica modal. Su principal contribución es una semántica para la lógica modal que involucra mundos posibles , ahora llamada semántica de Kripke . [6] Recibió el Premio Schock en Lógica y Filosofía en 2001.
Kripke también fue en parte responsable del resurgimiento de la metafísica y el esencialismo después del declive del positivismo lógico , afirmando que la necesidad es una noción metafísica distinta de la noción epistémica de a priori , y que hay verdades necesarias que se conocen a posteriori , como que el agua es H2O . Una serie de conferencias de Princeton de 1970, publicada en forma de libro en 1980 como Naming and Necessity , se considera una de las obras filosóficas más importantes del siglo XX. Introduce el concepto de nombres como designadores rígidos , que designan (seleccionan, denotan, se refieren a) el mismo objeto en cada mundo posible, en contraste con las descripciones . También contiene la teoría causal de la referencia de Kripke , cuestionando la teoría descriptivista que se encuentra en el concepto de sentido de Gottlob Frege y la teoría de las descripciones de Bertrand Russell . A menudo se opone a Kripke, otro gran filósofo de finales del siglo XX que rechazó el positivismo lógico: WVO Quine . Quine rechazó el esencialismo y la lógica modal. [7] [8]
Kripke también ofreció una lectura original de Ludwig Wittgenstein , conocido como " Kripkenstein ", en su obra Wittgenstein on Rules and Private Language . El libro contiene su argumento de seguimiento de reglas, una paradoja para el escepticismo sobre el significado . Gran parte de su obra permanece inédita o existe sólo en forma de grabaciones y manuscritos que circulan de forma privada.
Saul Kripke fue el mayor de los tres hijos de Dorothy K. Kripke y Myer S. Kripke . [9] Su padre era el líder de la sinagoga Beth El, la única congregación conservadora en Omaha , Nebraska ; su madre escribía libros educativos judíos para niños. Saul y sus dos hermanas, Madeline y Netta, asistieron a la escuela primaria Dundee y a la escuela secundaria Omaha Central High School . Kripke fue etiquetado como un prodigio , aprendiendo hebreo antiguo por sí mismo a la edad de seis años, leyendo las obras completas de Shakespeare a los nueve años y dominando las obras de Descartes y problemas matemáticos complejos antes de terminar la escuela primaria. [10] [11] Escribió su primer teorema de completitud en lógica modal a los 17 años, y lo publicó un año después. Después de graduarse de la escuela secundaria en 1958, Kripke asistió a la Universidad de Harvard y se graduó summa cum laude en 1962 con una licenciatura en matemáticas. Durante su segundo año en Harvard, enseñó un curso de lógica de nivel de posgrado en el cercano MIT . [12] Al graduarse, recibió una beca Fulbright y en 1963 fue nombrado miembro de la Society of Fellows . Kripke dijo más tarde: "Me hubiera gustado poder saltarme la universidad. Conocí a gente interesante, pero no puedo decir que aprendí nada. Probablemente lo habría aprendido todo de todos modos con solo leer por mi cuenta". [13] Su primo es Eric Kripke , conocido por crear el programa de televisión The Boys . [14]
Después de enseñar brevemente en Harvard, Kripke se trasladó en 1968 a la Universidad Rockefeller en la ciudad de Nueva York, donde enseñó hasta 1976. En 1978 asumió una cátedra en la Universidad de Princeton . [15] En 1988 recibió el Premio Behrman de la universidad por logros distinguidos en humanidades. En 2002 Kripke comenzó a enseñar en el Centro de Graduados de CUNY , y en 2003 fue nombrado profesor distinguido de filosofía allí.
Kripke ha recibido títulos honorarios de la Universidad de Nebraska , Omaha (1977), la Universidad Johns Hopkins (1997), la Universidad de Haifa , Israel (1998) y la Universidad de Pensilvania (2005). Fue miembro de la Sociedad Filosófica Estadounidense y miembro electo de la Academia Estadounidense de las Artes y las Ciencias , y en 1985 fue miembro correspondiente de la Academia Británica . [16] Ganó el Premio Schock en Lógica y Filosofía en 2001. [17]
Kripke estuvo casado con la filósofa Margaret Gilbert .
Kripke murió de cáncer de páncreas el 15 de septiembre de 2022, en Plainsboro, Nueva Jersey, a la edad de 81 años. [18] [19] [20]
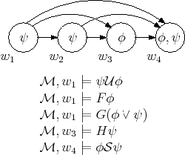
Las contribuciones de Kripke a la filosofía incluyen:
También ha contribuido a la teoría de la recursión (véase teoría de conjuntos ordinales admisibles y de Kripke-Platek ).
Dos de los primeros trabajos de Kripke, "Un teorema de completitud en lógica modal" (1959) [21] y "Consideraciones semánticas sobre lógica modal" (1963), el primero escrito cuando era adolescente, trataban sobre lógica modal . Las lógicas más conocidas de la familia modal se construyen a partir de una lógica débil llamada K, llamada así en honor a Kripke. Kripke introdujo la semántica de Kripke , ahora estándar (también conocida como semántica relacional o semántica de marco) para lógicas modales. La semántica de Kripke es una semántica formal para sistemas lógicos no clásicos. Primero se hizo para lógicas modales y luego se adaptó a la lógica intuicionista y otros sistemas no clásicos. El descubrimiento de la semántica de Kripke fue un gran avance en la creación de lógicas no clásicas, porque la teoría de modelos de tales lógicas no existía antes de Kripke.
Un marco de Kripke o marco modal es un par , donde W es un conjunto no vacío y R es una relación binaria en W. Los elementos de W se denominan nodos o mundos , y R se conoce como la relación de accesibilidad . Dependiendo de las propiedades de la relación de accesibilidad ( transitividad , reflexividad, etc.), el marco correspondiente se describe, por extensión, como transitivo, reflexivo, etc.
Un modelo de Kripke es un triple , donde es un marco de Kripke, y es una relación entre nodos de W y fórmulas modales, tales que:
Leemos como " w satisface A ", " A se satisface en w ", o " w fuerza a A ". La relación se llama relación de satisfacción , evaluación o relación de forzamiento . La relación de satisfacción está determinada únicamente por su valor en variables proposicionales.
Una fórmula A es válida en:
Definimos Thm( C ) como el conjunto de todas las fórmulas que son válidas en C . Por el contrario, si X es un conjunto de fórmulas, sea Mod( X ) la clase de todos los marcos que validan cada fórmula de X .
Una lógica modal (es decir, un conjunto de fórmulas) L es válida con respecto a una clase de marcos C , si L ⊆ Thm( C ). L es completa con respecto a C si L ⊇ Thm( C ).
La semántica es útil para investigar una lógica (es decir, un sistema de derivación) sólo si la relación de implicación semántica refleja su contraparte sintáctica, la relación de consecuencia ( derivabilidad ). Es vital saber qué lógicas modales son sólidas y completas con respecto a una clase de marcos de Kripke y, en el caso de ellas, determinar a qué clase pertenecen.
Para cualquier clase C de sistemas Kripkeanos, Thm( C ) es una lógica modal normal (en particular, los teoremas de la lógica modal normal mínima, K , son válidos en cada modelo Kripkeano). Sin embargo, la recíproca no se cumple en general. Existen lógicas modales normales Kripkeanas incompletas, lo cual no es problemático, porque la mayoría de los sistemas modales estudiados están completos de clases de sistemas descriptos por condiciones simples.
Una lógica modal normal L corresponde a una clase de marcos C , si C = Mod( L ). En otras palabras, C es la clase más grande de marcos tal que L es sólida con respecto a C . De ello se deduce que L es completa en términos de Kripke si y solo si es completa en su clase correspondiente.
Considérese el esquema T : . T es válido en cualquier marco reflexivo : si , entonces como w R w . Por otra parte, un marco que valida T tiene que ser reflexivo: fijar w ∈ W , y definir la satisfacción de una variable proposicional p de la siguiente manera: si y sólo si w R u . Entonces , por tanto por T , lo que significa w R w usando la definición de . T corresponde a la clase de marcos reflexivos de Kripke.
A menudo es mucho más fácil caracterizar la clase correspondiente de L que probar su completitud, por lo que la correspondencia sirve como guía para las pruebas de completitud. La correspondencia también se utiliza para mostrar la incompletitud de las lógicas modales: supongamos que L 1 ⊆ L 2 son lógicas modales normales que corresponden a la misma clase de marcos, pero L 1 no prueba todos los teoremas de L 2 . Entonces L 1 es incompleto en el sentido de Kripke. Por ejemplo, el esquema genera una lógica incompleta, ya que corresponde a la misma clase de marcos que GL (es decir, marcos bien fundados transitivos y conversos), pero no prueba la tautología GL .
Para cualquier lógica modal normal L , se puede construir un modelo de Kripke (llamado modelo canónico ) que valida con precisión los teoremas de L , mediante una adaptación de la técnica estándar de utilizar conjuntos consistentes máximos como modelos. Los modelos canónicos de Kripke desempeñan un papel similar a la construcción del álgebra de Lindenbaum-Tarski en la semántica algebraica.
Un conjunto de fórmulas es L - consistente si no se puede derivar ninguna contradicción de ellas utilizando los axiomas de L y modus ponens . Un conjunto L-consistente maximalista (un L - MCS para abreviar) es un conjunto L -consistente que no tiene un superconjunto L -consistente propio .
El modelo canónico de L es un modelo de Kripke , donde W es el conjunto de todos los L - MCS , y las relaciones R y son las siguientes:
El modelo canónico es un modelo de L , ya que cada L - MCS contiene todos los teoremas de L . Por el lema de Zorn , cada conjunto L -consistente está contenido en un L - MCS , en particular cada fórmula indemostrable en L tiene un contraejemplo en el modelo canónico.
La principal aplicación de los modelos canónicos son las pruebas de completitud. Las propiedades del modelo canónico de K implican inmediatamente la completitud de K con respecto a la clase de todos los marcos de Kripke. Este argumento no funciona para un L arbitrario , porque no hay garantía de que el marco subyacente del modelo canónico satisfaga las condiciones de marco de L.
Decimos que una fórmula o un conjunto X de fórmulas es canónica con respecto a una propiedad P de los marcos de Kripke, si
Una unión de conjuntos canónicos de fórmulas es en sí misma canónica. De la discusión anterior se desprende que cualquier lógica axiomatizada por un conjunto canónico de fórmulas es completa según Kripke y compacta .
Los axiomas T, 4, D, B, 5, H, G (y, por tanto, cualquier combinación de ellos) son canónicos. GL y Grz no son canónicos, porque no son compactos. El axioma M por sí mismo no es canónico ( Goldblatt , 1991), pero la lógica combinada S4.1 (de hecho, incluso K4.1 ) sí lo es.
En general, no se puede decidir si un axioma dado es canónico. Conocemos una buena condición suficiente: H. Sahlqvist identificó una amplia clase de fórmulas (ahora llamadas fórmulas de Sahlqvist ) tales que:
Este es un criterio poderoso: por ejemplo, todos los axiomas enumerados anteriormente como canónicos son (equivalentes a) fórmulas de Sahlqvist. Una lógica tiene la propiedad de modelo finito (FMP) si es completa con respecto a una clase de marcos finitos. Una aplicación de esta noción es la cuestión de decidibilidad: se sigue del teorema de Post que una lógica modal recursivamente axiomatizada L que tiene FMP es decidible, siempre que sea decidible si un marco finito dado es un modelo de L. En particular, toda lógica finitamente axiomatizable con FMP es decidible.
Existen varios métodos para establecer el FMP para una lógica dada. Los refinamientos y extensiones de la construcción del modelo canónico suelen funcionar, utilizando herramientas como la filtración o el desenredo. Como otra posibilidad, las pruebas de completitud basadas en cálculos de secuencias sin cortes suelen producir modelos finitos directamente.
La mayoría de los sistemas modales utilizados en la práctica (incluidos todos los enumerados anteriormente) tienen FMP.
En algunos casos, podemos usar FMP para probar la completitud de Kripke de una lógica: toda lógica modal normal es completa con respecto a una clase de álgebras modales, y un álgebra modal finita se puede transformar en un marco de Kripke. Como ejemplo, Robert Bull demostró usando este método que toda extensión normal de S4.3 tiene FMP y es completa según Kripke.
La semántica de Kripke tiene una generalización directa a lógicas con más de una modalidad. Un marco de Kripke para un lenguaje con como conjunto de sus operadores de necesidad consiste en un conjunto no vacío W equipado con relaciones binarias R i para cada i ∈ I . La definición de una relación de satisfacción se modifica de la siguiente manera:
Una semántica simplificada, descubierta por Tim Carlson, se utiliza a menudo para lógicas de demostrabilidad polimodal . [22] Un modelo de Carlson es una estructura con una única relación de accesibilidad R y subconjuntos D i ⊆ W para cada modalidad. La satisfacción se define como:
Los modelos de Carlson son más fáciles de visualizar y trabajar con ellos que los modelos polimodales Kripke habituales; sin embargo, existen lógicas polimodales completas de Kripke que son incompletas desde el punto de vista de Carlson.
En Consideraciones semánticas sobre la lógica modal , publicado en 1963, Kripke respondió a una dificultad de la teoría de cuantificación clásica . La motivación del enfoque relativo al mundo era representar la posibilidad de que los objetos de un mundo puedan no existir en otro. Pero si se utilizan las reglas estándar de cuantificación, cada término debe referirse a algo que existe en todos los mundos posibles. Esto parece incompatible con nuestra práctica habitual de utilizar términos para referirnos a cosas que existen de manera contingente.
La respuesta de Kripke a esta dificultad fue eliminar términos. Puso como ejemplo un sistema que utiliza la interpretación relativa al mundo y conserva las reglas clásicas. Pero los costos son altos. En primer lugar, su lenguaje se empobrece artificialmente y, en segundo lugar, las reglas de la lógica modal proposicional deben debilitarse.
La teoría de los mundos posibles de Kripke ha sido utilizada por narratólogos (empezando por Pavel y Dolezel) para comprender "la manipulación que hace el lector de desarrollos alternativos de la trama, o de series de acciones alternativas planificadas o fantaseadas por los personajes". Esta aplicación se ha vuelto especialmente útil en el análisis de la hiperficción . [23]
La semántica de Kripke para la lógica intuicionista sigue los mismos principios que la semántica de la lógica modal, pero utiliza una definición diferente de satisfacción.
Un modelo Kripke intuicionista es un triple , donde es un marco Kripke parcialmente ordenado , y satisface las siguientes condiciones:
La lógica intuicionista es sólida y completa con respecto a su semántica Kripke, y tiene la propiedad del modelo finito.
Lógica intuicionista de primer orden
Sea L un lenguaje de primer orden . Un modelo Kripke de L es una tripleta , donde es un marco Kripke intuicionista, M w es una L -estructura (clásica) para cada nodo w ∈ W , y las siguientes condiciones de compatibilidad se cumplen siempre que u ≤ v :
Dada una evaluación e de variables por elementos de M w , definimos la relación de satisfacción :
Aquí e ( x → a ) es la evaluación que da a x el valor a , y por lo demás concuerda con e .

Las tres conferencias que forman Naming and Necessity constituyen un ataque a la teoría descriptivista de los nombres . Kripke atribuye variantes de las teorías descriptivistas a Frege , Russell , Wittgenstein y John Searle , entre otros. Según las teorías descriptivistas, los nombres propios son sinónimos de descripciones o tienen su referencia determinada en virtud de que el nombre está asociado con una descripción o conjunto de descripciones que un objeto satisface de manera única. Kripke rechaza ambos tipos de descriptivismo. Da varios ejemplos que pretenden hacer que el descriptivismo sea inverosímil como teoría de cómo los nombres obtienen sus referencias determinadas (por ejemplo, seguramente Aristóteles podría haber muerto a los dos años y, por lo tanto, no satisfacer ninguna de las descripciones que asociamos con su nombre, pero parecería incorrecto negar que todavía era Aristóteles).
Como alternativa, Kripke esbozó una teoría causal de la referencia , según la cual un nombre se refiere a un objeto en virtud de una conexión causal con el objeto mediada a través de comunidades de hablantes. Señala que los nombres propios, en contraste con la mayoría de las descripciones, son designadores rígidos : es decir, un nombre propio se refiere al objeto nombrado en cada mundo posible en el que existe el objeto, mientras que la mayoría de las descripciones designan diferentes objetos en diferentes mundos posibles. Por ejemplo, "Richard Nixon" se refiere a la misma persona en cada mundo posible en el que existe Nixon, mientras que "la persona que ganó las elecciones presidenciales de los Estados Unidos de 1968" podría referirse a Nixon , Humphrey u otros en diferentes mundos posibles.
Kripke también planteó la posibilidad de necesidades a posteriori , es decir, hechos que son necesariamente ciertos , aunque sólo se puedan conocer a través de la investigación empírica. Algunos ejemplos son « Héspero es fósforo », « Cicerón es Tulio », «El agua es H2O » y otras afirmaciones de identidad en las que dos nombres se refieren al mismo objeto. Según Kripke, las distinciones kantianas entre analítico y sintético, a priori y a posteriori , y contingente y necesario no se corresponden entre sí. Más bien, analítico/sintético es una distinción semántica, a priori / a posteriori es una distinción epistémica y contingente/necesario es una distinción metafísica.
Finalmente, Kripke presentó un argumento contra el materialismo de identidad en la filosofía de la mente , la visión de que cada particular mental es idéntico a algún particular físico. Kripke argumentó que la única manera de defender esta identidad es como una identidad necesaria a posteriori , pero que tal identidad (por ejemplo, que el dolor es la activación de las fibras C ) no podría ser necesaria, dada la posibilidad (claramente concebible) de que el dolor pudiera estar separado de la activación de las fibras C, o la activación de las fibras C estuviera separada del dolor. (Argumentos similares han sido presentados posteriormente por David Chalmers . [24] ) En cualquier caso, el teórico de la identidad psicofísica, según Kripke, incurre en una obligación dialéctica de explicar la aparente posibilidad lógica de estas circunstancias, ya que según tales teóricos deberían ser imposibles.
Kripke dictó las John Locke Lectures de filosofía en Oxford en 1973. Tituladas Reference and Existence , fueron en muchos aspectos una continuación de Naming and Necessity y tratan los temas de los nombres ficticios y el error perceptivo. En 2013, Oxford University Press publicó las conferencias como un libro, también titulado Reference and Existence .
En un artículo de 1995, el filósofo Quentin Smith argumentó que los conceptos clave en la nueva teoría de la referencia de Kripke se originaron en el trabajo de Ruth Barcan Marcus más de una década antes. [25] Smith identificó seis ideas significativas en la Nueva Teoría que, según él, Marcus había desarrollado: (1) que los nombres propios son referencias directas que no consisten en definiciones contenidas; (2) que si bien uno puede distinguir una sola cosa por una descripción, esta descripción no es equivalente a un nombre propio de esta cosa; (3) el argumento modal de que los nombres propios son directamente referenciales y no descripciones disfrazadas; (4) una prueba de lógica modal formal de la necesidad de identidad ; (5) el concepto de un designador rígido , aunque Kripke acuñó ese término; y (6) identidad a posteriori . Smith argumentó que Kripke no entendió la teoría de Marcus en ese momento, pero luego adoptó muchos de sus temas conceptuales clave en su Nueva Teoría de la Referencia.
Otros académicos han ofrecido posteriormente respuestas detalladas argumentando que no se produjo ningún plagio. [26] [27]
Las principales proposiciones de Kripke sobre los nombres propios en Naming and Necessity son que el significado de un nombre es simplemente el objeto al que se refiere y que el referente de un nombre está determinado por un vínculo causal entre algún tipo de "bautismo" y la pronunciación del nombre. Sin embargo, reconoce la posibilidad de que las proposiciones que contienen nombres puedan tener algunas propiedades semánticas adicionales, [28] propiedades que podrían explicar por qué dos nombres que se refieren a la misma persona pueden dar diferentes valores de verdad en proposiciones sobre creencias. Por ejemplo, Lois Lane cree que Superman puede volar, aunque no cree que Clark Kent pueda volar. Esto se puede explicar si los nombres "Superman" y "Clark Kent", aunque se refieren a la misma persona, tienen propiedades semánticas distintas.
Pero en su artículo "A Puzzle about Belief" (1988) Kripke parece oponerse incluso a esta posibilidad. Su argumento puede reconstruirse de la siguiente manera: la idea de que dos nombres que se refieren al mismo objeto pueden tener diferentes propiedades semánticas supuestamente explica que los nombres correferentes se comporten de manera diferente en proposiciones sobre creencias (como en el caso de Lois Lane). Pero el mismo fenómeno ocurre incluso con nombres correferentes que obviamente tienen las mismas propiedades semánticas: Kripke nos invita a imaginar a un niño francés monolingüe, Pierre, que cree que " Londres est jolie " ("Londres es hermoso"). Pierre se muda a Londres sin darse cuenta de que Londres = Londres. Luego aprende inglés de la misma manera que un niño aprendería el idioma, es decir, no traduciendo palabras del francés al inglés. Pierre aprende el nombre "Londres" de la parte poco atractiva de la ciudad donde vive, y así llega a creer que Londres no es hermoso. Si la explicación de Kripke es correcta, Pierre ahora cree tanto que Londres es jolie como que Londres no es hermoso. Esto no se puede explicar mediante la correlación de nombres que tienen diferentes propiedades semánticas. Según Kripke, esto demuestra que atribuir propiedades semánticas adicionales a los nombres no explica lo que se pretende.
Publicado por primera vez en 1982, el libro de Kripke Wittgenstein sobre reglas y lenguaje privado sostiene que el argumento central de las Investigaciones filosóficas de Wittgenstein se centra en una devastadora paradoja del seguimiento de reglas que socava la posibilidad de que siempre sigamos reglas en nuestro uso del lenguaje. Kripke escribe que esta paradoja es "el problema escéptico más radical y original que la filosofía ha visto hasta la fecha", y que Wittgenstein no rechaza el argumento que conduce a la paradoja del seguimiento de reglas, sino que lo acepta y ofrece una "solución escéptica" para mejorar los efectos destructivos de la paradoja.
La mayoría de los comentaristas aceptan que Investigaciones filosóficas contiene la paradoja del seguimiento de reglas tal como la presenta Kripke, pero pocos han estado de acuerdo con que atribuya una solución escéptica a Wittgenstein. El propio Kripke expresa dudas en Wittgenstein sobre las reglas y el lenguaje privado sobre si Wittgenstein respaldaría su interpretación de Investigaciones filosóficas. Dice que la obra no debe leerse como un intento de dar una declaración precisa de las opiniones de Wittgenstein, sino más bien como una explicación del argumento de Wittgenstein "tal como impactó a Kripke, tal como le planteó un problema".
La interpretación de Kripke de las Investigaciones filosóficas se ha denominado "Kripkenstein" . El significado principal de Kripkenstein fue la clara declaración de un nuevo tipo de escepticismo, denominado "escepticismo del significado": la idea de que para los individuos aislados no existe ningún hecho en virtud del cual quieran decir una cosa en lugar de otra mediante el uso de una palabra. La "solución escéptica" de Kripke al escepticismo del significado consiste en fundamentar el significado en el comportamiento de una comunidad.
El libro de Kripke generó una gran literatura secundaria, dividida entre aquellos que encuentran su problema escéptico interesante y perspicaz, y otros, como Gordon Baker , Peter Hacker y Colin McGinn , que sostienen que su escepticismo sobre el significado es un pseudoproblema que surge de una lectura confusa y selectiva de Wittgenstein. La posición de Kripke ha sido defendida contra estos y otros ataques por el filósofo de Cambridge Martin Kusch , y el estudioso de Wittgenstein David G. Stern considera el libro de Kripke como "el trabajo más influyente y ampliamente discutido" sobre Wittgenstein desde la década de 1980. [29]
En su artículo de 1975 "Esquema de una teoría de la verdad", Kripke demostró que un lenguaje puede contener consistentemente su propio predicado de verdad , algo que Alfred Tarski , un pionero en las teorías formales de la verdad, consideró imposible. El enfoque implica dejar que la verdad sea una propiedad parcialmente definida sobre el conjunto de oraciones gramaticalmente bien formadas en el lenguaje. Kripke mostró cómo hacer esto de manera recursiva comenzando desde el conjunto de expresiones en un lenguaje que no contienen el predicado de verdad y definiendo un predicado de verdad solo sobre ese segmento: esta acción agrega nuevas oraciones al lenguaje y, a su vez, la verdad se define para todas ellas. Sin embargo, a diferencia del enfoque de Tarski, el de Kripke permite que la "verdad" sea la unión de todas estas etapas de definición; después de una infinidad numerable de pasos, el lenguaje alcanza un "punto fijo" tal que usar el método de Kripke para expandir el predicado de verdad no cambia más el lenguaje. Ese punto fijo puede entonces tomarse como la forma básica de un lenguaje natural que contiene su propio predicado de verdad. Pero este predicado no está definido para ninguna oración que, por así decirlo, no "toque fondo" en oraciones más simples que no contengan un predicado de verdad. Es decir, "'La nieve es blanca' es verdadera" está bien definido, como lo está "'La nieve es blanca' es verdadera' es verdadera", y así sucesivamente, pero ni "Esta oración es verdadera" ni "Esta oración no es verdadera" reciben condiciones de verdad; son, en términos de Kripke, "infundadas".

El primer teorema de incompletitud de Gödel demuestra que la autorreferencia no puede evitarse ingenuamente, ya que las proposiciones sobre objetos aparentemente no relacionados (como los números enteros) pueden tener un significado autorreferencial informal, y esta idea –manifestada por el lema diagonal– es la base del teorema de Tarski de que la verdad no puede definirse consistentemente. Pero el predicado de verdad de Kripke no otorga un valor de verdad (verdadero/falso) a proposiciones como la construida en la prueba de Tarski, ya que es demostrable por inducción que no está definido en esta etapa para cada número finito .
La propuesta de Kripke es problemática en el sentido de que, si bien el lenguaje contiene un predicado de "verdad" de sí mismo (al menos uno parcial), algunas de sus oraciones –como la oración del mentiroso ("esta oración es falsa")– tienen un valor de verdad indefinido, pero el lenguaje no contiene su propio predicado "indefinido". De hecho, no puede, ya que eso crearía una nueva versión de la paradoja del mentiroso , la paradoja del mentiroso reforzada ("esta oración es falsa o indefinida"). Por lo tanto, si bien la oración del mentiroso no está definida en el lenguaje, el lenguaje no puede expresar que no está definida. [30]
El Centro Saul Kripke del Graduate Center de la City University de Nueva York se dedica a preservar y promover la obra de Kripke. Su directora es Romina Padro. El Centro Saul Kripke organiza eventos relacionados con la obra de Kripke y está creando un archivo digital de grabaciones inéditas de conferencias, notas de conferencias y correspondencia de Kripke que se remontan a la década de 1950. [31] En su reseña favorable de Philosophical Troubles de Kripke , el filósofo de Stanford Mark Crimmins escribió: "El hecho de que cuatro de los ensayos más admirados y discutidos de la filosofía de la década de 1970 estén aquí es suficiente para hacer de este primer volumen de los artículos recopilados de Saul Kripke un artículo imprescindible... El deleite del lector aumentará a medida que se den pistas de que hay mucho más por venir en esta serie que está preparando Kripke y un equipo de filósofos-editores de primer nivel en el Centro Saul Kripke del Graduate Center de la City University de Nueva York". [32]
{{cite journal}}: Requiere citar revista |journal=( ayuda )