Triángulo de Reuleaux

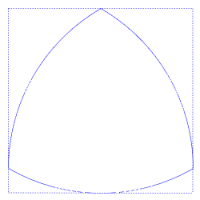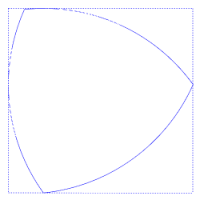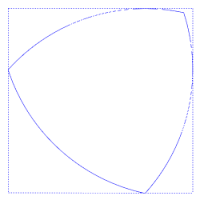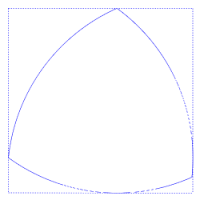
Esto puede apreciarse en la figura adjunta, en la que siempre hay cuatro puntos de tangencia con el cuadrado, uno en cada lado.

Es un triángulo curvo con anchura constante, la curva de anchura constante más simple y mejor conocida aparte del círculo.

Deben su nombre a Franz Reuleaux,[1]​ Ingeniero alemán del siglo XIX, pionero en el estudio de las máquinas que traducen un tipo de movimiento en otro y que utilizó triángulos de Reuleaux en sus diseños.

Entre las formas de anchura constante con una anchura dada, el triángulo de Reuleaux tiene el área mínima y el ángulo más agudo (más pequeño) posible (120°) en sus esquinas.

Según varias medidas numéricas, es la forma más alejada de la simétrica central.

Proporciona la mayor forma de ancho constante evitando los puntos de un entramado entero, y está estrechamente relacionada con la forma del cuadrilátero que maximiza la relación entre el perímetro y el diámetro.

Puede realizar una rotación completa dentro de un cuadrado tocando en todo momento los cuatro lados del cuadrado, y tiene el área más pequeña posible de las formas con esta propiedad.

Borrando el triángulo inicial, el espacio central que delimitan en común las tres cirunferencias es el triángulo de Reuleaux, una curva de anchura constante.

[12]​ Reuleaux utilizó estos modelos en sus investigaciones científicas pioneras sobre su movimiento.

En esta aplicación, es necesario hacer avanzar la película con un movimiento espasmódico y escalonado, en el que cada fotograma de la película se detiene durante una fracción de segundo delante de la lente del proyector, y luego, mucho más rápidamente, la película pasa al siguiente fotograma.

[20]​ Se pueden utilizar métodos similares para encerrar un polígono simple arbitrario dentro de una curva de anchura constante, cuya anchura es igual al diámetro del polígono dado.

La forma resultante consiste en arcos circulares (a lo sumo tantos como lados tenga el polígono), puede construirse algorítmicamente en tiempo lineal, y puede dibujarse con compás y regla.

[22]​ Los conjuntos de Yanmouti se definen como los cascos convexos de un triángulo equilátero junto con tres arcos circulares, centrados en los vértices del triángulo y que abarcan el mismo ángulo que el triángulo, con radios iguales que son como máximo iguales a la longitud lateral del triángulo.

Así, cuando el radio es suficientemente pequeño, estos conjuntos degeneran en el propio triángulo equilátero, pero cuando el radio es lo más grande posible son iguales al triángulo de Reuleaux correspondiente.

Toda forma con anchura w, diámetro d, e inradio r (el radio del círculo más grande posible contenido en la forma) obedece a la desigualdad y esta desigualdad se convierte en una igualdad para los conjuntos de Yanmouti, lo que demuestra que no es mejorable.

[1]​ Los mismos tres círculos forman uno de los dibujos estándar de los anillos borromeos, tres anillos mutuamente enlazados que, sin embargo, no pueden realizarse como círculos geométricos.

Para un amplio rango de elecciones del parámetro área, la solución óptima a este problema será un triángulo curvo cuyos tres lados son arcos circulares con radios iguales.

En particular, cuando los tres puntos son equidistantes entre sí y el área es la del triángulo de Reuleaux, el triángulo de Reuleaux es el recinto óptimo.

[28]​ Otras formas planas con tres lados curvos incluyen el arbelos, que se forma a partir de tres semicírculos con puntos extremos colineales,[29]​ y el triángulo de Bézier.