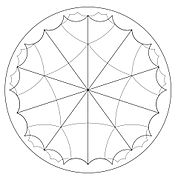
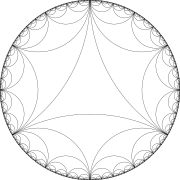
Triángulo de Schwarz

Los bordes de valor 2 representan espejos perpendiculares (ángulo Π/2 = 90°), que se pueden ignorar en este diagrama.Para un triángulo ideal en el que todos los ángulos sean cero, de modo que todos sus vértices estén sobre el eje real, la existencia del teselado se establecerá relacionándolo con la sucesión de Farey descrita en Hardy y Wright (2008) y Series (2015).Los triángulos no se superponen excepto en los bordes, la mitad de ellos tienen su orientación invertida y encajan entre sí para teselar un entorno del punto.Está formado por triángulos que solo se intersecan en las aristas o vértices, forma un polígono convexo con todos los ángulos menores o iguales a Π y cada lado es la arista de un triángulo reflejado.Esto da como resultado un total de 3 + (2a – 3) + (2b - 3) + (2c - 3) = 2(a + b + c) - 6 nuevos triángulos.Por inducción, los radios OA y OB forman ángulos menores o iguales a 2Π/3 con la arista AB.Ahora las teselas adicionales añadidas en A se encuentran en el sector definido por los radios OB1 y OB2.Finalmente queda probar que el teselado formado por la unión de los triángulos cubre la totalidad del semiplano superior.Si 2Π/b ≤ Π/3, es decir, b es mayor que 5, y entonces todos los ángulos del triángulo reflejado son menores o iguales a Π/3.El método anterior para construir P2, P3, ... se modifica agregando un triángulo adicional cada vez que surge un ángulo 3Π/2 en un vértice.El proceso se puede continuar de esta forma para obtener polígonos convexos P3, P4 y así sucesivamente.El interior de tal triángulo se puede realizar como la región X en el semiplano superior que se encuentra fuera del disco unitario |z| = 1 y entre dos líneas paralelas al eje imaginario a través de los puntos u y v en el círculo unitario.Las tres reflexiones en los lados están dadas por Así T = R3°R2 es una traslación de valor µ - λ.Continuando de esta manera, o bien algún wn satisface que |wn| = 1, en cuyo caso se prueba el resultado; o bien |wn| < 1 para todo n. De esta manera, gn + 1 está en Γ1 y |wn| < 1, y entonces En particular y Así, de la desigualdad anterior, se deduce que los puntos (wn) se encuentran en el conjunto compacto |z| = 1, λ = Re z = µ e Im z = Im w 1.Así, w se encuentra en el arco del círculo unitario entre u y v.Si w ≠ u, v, entonces R1 wn estaría en X para n lo suficientemente grande, al contrario de la suposición realizada.Sea ahora Aplicando S si es necesario, se puede suponer que |a| > |c| (la igualdad no es posible por su condición de coprimos).Pero entonces Este proceso puede continuar hasta que una de las entradas sea 0, en cuyo caso la otra es necesariamente ±1.Dado que los triángulos en el teselado son exactamente aquellos de la forma gΔ con g en Γ, se deduce que S y T, y por lo tanto todos los elementos de G, permutan triángulos en el teselado.La imagen P(Σ), es decir, la unión de las traslaciones g(Δ), es por lo tanto un subconjunto abierto del semiplano superior.Ahora, se debe establecer que A = (cos Π / a) si a ≥ 2 es finito y cosh x con x > 0; de lo contrario; establecer de manera similar que B = cos Π / b o cosh y y C = cos Π / c o cosh z.[23]​ Sean er, es y et una base para un espacio vectorial real tridimensional V con forma bilineal simétrica Λ tal que Λ(es,et) = - A, Λ(et,er) = - B y Λ( er,es) = - C, con las tres entradas diagonales iguales a uno.Los operadores ρ, σ y τ inducen una representación de Γ sobre V que conserva Λ.Como resultado, dos valores propios son positivos y uno negativo, es decir, Λ tiene la signatura (2,1).Manifiestamente ρ, σ y τ son involuciones, preservándose Λ con los vectores propios asociados a -1 dados.Para (2), U es invariante por definición y la matriz es definida positiva ya que 0 < cos Π / a < 1.Por ejemplo, esto se puede deducir de la observación de Paul Halmos y otros, que el operador autoadjunto positivo (S – T)2 conmuta tanto con S como con T. Sin embargo, en el caso anterior, donde la forma bilineal Λ ya no es un producto interno definido positivo, se debe dar un razonamiento "ad hoc" diferente.[27]​ Es una rutina comprobar a partir de las definiciones que:[28]​ Proposición: Si g está en Γ y ℓ(gq) = ℓ(g) ± 1 para una reflexión simple q, entonces geq se encuentra en ±X, y es por tanto raíz positiva o negativa, según el signo.Por lo tanto, basta mostrar que kes tiene la forma λes + μet con λ, μ = 0, no ambos 0.La reflexión simple q permuta toda raíz positiva que no sea eq.El grupo discreto Γ actúa discontinuamente sobre G / K: el espacio cociente Γ G / K es compacto si a, b y c son todos finitos, y de área finita en caso contrario.