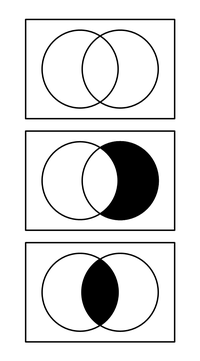
Diagrama de Venn

La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

[2]​ Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

Variantes de la misma fueron empleadas luego por George Boole y Augustus De Morgan, pero fue el gran matemático suizo Leonhard Euler quien primero introdujo una notación clara y sencilla.

[1]​ El conjunto universal fue cuestionado por Bertrand Russell, quien mostró que con tal concepto la teoría de conjuntos resultaba inconsistente (véase paradoja de Russell).

Sin embargo, dicha definición fue rescatada y aun justificada en una reciente extensión de los diagramas de Venn que distingue al universal del Todo (universo del discurso).

Este libro sirvió sobre todo para presentar ejemplos del uso de los diagramas.

[12]​ Los siguientes diagramas muestran la cantidad de regiones en que queda dividido el conjunto universal con una, dos y tres definiciones.

El área donde las dos regiones se superponen contiene por lo tanto a todos los animales que, al mismo tiempo, son bípedos y pueden volar.

Los diagramas de tres conjuntos fueron los más usados por Venn en toda su obra.

Un cuarto conjunto puede ser representado tomando una curva similar a la juntura de una pelota de tenis que suba y baje alrededor del ecuador.

Edwards ideó estos diagramas mientras diseñaba la ventana acristalada en memoria de Venn que hoy adorna el comedor del Caius College.

Por su parte, Lewis Carroll diseñó un diagrama de cinco conjuntos.

[2]​ Los diagramas de Venn son útiles en muchas áreas, incluyendo las matemáticas, la estadística, la lógica y la informática.