Pentágono
La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es: El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5): Un pentágono regular es construible usando un compás y una regla, ya sea inscribiendo uno en un círculo dado o construyendo uno en un lado dado.
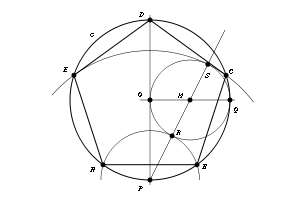
Euclides describió este proceso en sus Elementos, alrededor del año 300 a. C.[3][4] Se puede construir con regla y compás un pentágono regular, inscrito en una circunferencia (véase la figura), de la siguiente manera: Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él.
En el centro quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.
Un método para construir un pentágono regular en un círculo dado es el descrito por Richmond[5] y discutido con más detalle en Polyhedra de Cromwell.
Una recta horizontal que pasa por Q corta al círculo en el punto P, y la cuerda PD es el lado necesario del pentágono inscrito.
Para determinar la longitud de este lado, se representan debajo del círculo los dos triángulos rectángulos DCM y QCM.
Utilizando el teorema de Pitágoras y dos lados, se halla la hipotenusa del triángulo mayor como
[7] Esta metodología conduce a un procedimiento para construir un pentágono regular.
Los pasos son los siguientes:[8] Los pasos 6-8 son equivalentes a la siguiente versión, mostrada en la animación: Un pentágono equilátero es un polígono con cinco lados de igual longitud.
En cambio, el pentágono regular es único hasta la semejanza, porque es equilátero y es equiangular (sus cinco ángulos son iguales).
Un cíclico pentágono es aquel en el que una circunferencia, llamada circunscrita, pasa por los cinco vértices.
[13]: p.75, #1854 Un pentágono regular no puede aparecer en ningún mosaico de polígonos regulares.
No existen combinaciones de polígonos regulares con 4 o más vértices que contengan un pentágono.
Para combinaciones con 3, si 3 polígonos se encuentran en un vértice y uno tiene un número impar de lados, los otros 2 deben ser congruentes.
Para el pentágono, esto resulta en un polígono cuyos ángulos son todos (360 - 108) / 2 = 126°.
Por lo tanto, un pentágono no puede aparecer en ningún mosaico formado por polígonos regulares.
Hay 15 clases de pentágonos que pueden alicatar monohedralmente el plano.
Observamos que los triángulos ANF y CMF son semejantes.
Por otra parte, como el triángulo FCD es isósceles, tenemos que FC = CD.
es el único número positivo que cuando le restamos la unidad, obtenemos su inverso.
El ángulo MOB, suma de estos dos vale 108° y como el triángulo AOB es isósceles tenemos que Así, sea P la intersección de las rectas OA y MB.