Efecto Coriolis

Este efecto consiste en la existencia de una aceleración relativa del cuerpo en dicho sistema en rotación.

El cañón está girando con la tierra hacia el este y, por tanto, imprime al proyectil esa velocidad (además de la velocidad hacia adelante al momento de la impulsión).

En ese artículo, la fuerza de Coriolis aparece como una componente suplementaria a la fuerza centrífuga experimentada por un cuerpo en movimiento relativo a un referencial en rotación, como puede producirse, por ejemplo, en los engranajes de una máquina.

Esta fuerza no comenzó a aparecer en la literatura meteorológica y oceanográfica hasta finales del siglo XIX.

El término fuerza de Coriolis apareció a principios del siglo XX.

Para demostrar la expresión analítica expresada en la introducción, pueden usarse dos aproximaciones diferentes: por conservación del momento angular o por derivación en base móvil.

En el caso de un sistema en rotación, el observador ve que todos los objetos que no están sujetos se alejan de manera radial como si actuase sobre ellos una fuerza proporcional a sus masas y a la distancia a una cierta recta (el eje de rotación).

Si no lo están, los objetos tomarán la tangente y se alejarán del eje de rotación.

Visto desde el sistema en rotación, el movimiento de un objeto se puede descomponer en una componente paralela al eje de rotación, otra componente radial (situada sobre una línea que pasa por el eje de rotación y perpendicular a este), y una tercera componente tangencial (tangente a un círculo centrado en el eje y perpendicular a este) (ver gráfica).

Un objeto que se desplaza paralelamente al eje de rotación, visto desde un sistema fijo, gira con el sistema en rotación a la misma velocidad angular y con radio constante.

El observador del sistema en rotación sólo nota la fuerza centrífuga contra la cual hay que oponerse para que se quede a la misma distancia del eje.

Si la masa se moviese siguiendo una trayectoria radial, fija con respecto al sistema en rotación, conservando en consecuencia la misma velocidad angular

Para un observador fijo, entre la velocidad de la masa que se ve obligada a seguir una trayectoria radial y la velocidad de la masa que conserva su momento angular hay una diferencia de: Como el objeto no está sujeto al sistema en rotación, el observador en ese sistema ve la masa tomar una velocidad lateral

Esta vez, la misma masa tenida por un hilo tiene una velocidad angular diferente del sistema en rotación.

Se calcula ahora la fuerza centrípeta que ve un observador fijo: la velocidad tangencial es

Para este observador, la fuerza centrípeta que mantiene la masa a distancia constante será: El primer término es la fuerza centrífuga común a todos los objetos que giran con el sistema en rotación.

Es un término suplementario debido al hecho de que la fuerza centrípeta depende del cuadrado de la velocidad tangencial y no puede obtenerse sumando las fuerzas centrífuga y centrípeta debido a velocidades parciales.

[2]​ En efecto, los vientos o corrientes oceánicas que se desplazan siguiendo un meridiano se desvían acelerando en la dirección de giro (este) si van hacia los polos o al contrario (oeste) si van hacia el ecuador.

Se puede añadir, que por consecuencia, en el Ecuador, no hay efecto de Coriolis.

El efecto de Coriolis predice que siempre que se observen los movimientos giratorios de esos cuerpos, los vórtices seguirán la norma descrita para las borrascas y anticiclones terrestres.

En las cuencas que tienen la forma apropiada (como, por ejemplo, la cuenca del Atlántico norte y la del Atlántico sur), el efecto Coriolis desvía a las corrientes marinas hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur, de la misma manera que sucede con la circulación general de los vientos.

A su vez, este "abombamiento" ocasiona una especie de obstáculo a la libre circulación y al libre intercambio de energía (oceánica y atmosférica) entre los dos hemisferios.

Cuando el cuerpo está cerca del ecuador, su distancia respecto al eje de la Tierra no cambia.

Si la trayectoria del cuerpo es este-oeste y sigue un paralelo, su distancia respecto al eje terrestre no varía, pero ya hemos visto que sentirá una aceleración de Coriolis dirigida hacia el eje de la Tierra que vale

, lo cual corresponde a una fuerza lateral aproximadamente 100 000 veces menor que su propio peso.

Si se trata de un avión cuya velocidad es 900 km/h (250 m/s), la aceleración será 250 veces mayor.

Este componente vertical del efecto Coriolis es mayor en el ecuador, y se reduce a cero en los polos.

Otro caso a tener en cuenta es el de objetos que viajan en dirección perpendicular al plano terrestre.

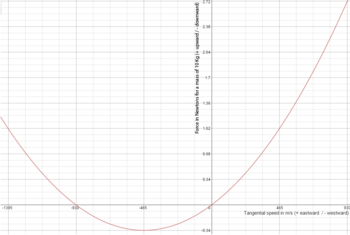
Imaginemos un tren que viaja por una vía sin rozamiento alrededor del ecuador de la Tierra a la velocidad necesaria para completar una vuelta al mundo en un día (465 m/s).

El mismo instrumento puede usarse para medir la densidad del fluido.