Reacción mecánica
En ingeniería estructural e ingeniería mecánica, una reacción es una fuerza de sujeción de un elemento resistente al suelo u otro elemento de grandes dimensiones que sirve de soporte al elemento resistente.
En sentido general a veces se habla de momentos de empotramiento o momentos reacción, en el caso de enlaces que además impiden el giro de algunas secciones de unión.
El cálculo de reacciones involucra calcular un número de parámetros (fuerzas o momentos) es mayor o igual que el número de grados de libertad eliminen las uniones con el exterior de una estructura o mecanismo.
Si el número de reacciones incógnita es inferior a tres el elemento resistente considerado es un mecanismo y requiere en general un cálculo dinámico para determinar completamente las reacciones.
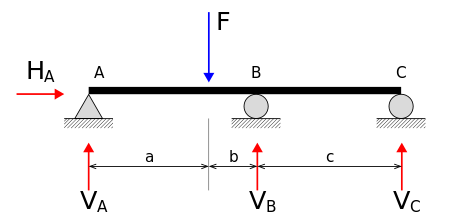
Si el número de reacciones incógnita es igual a tres, tenemos una estructura externamente isostática y las ecuaciones de la estática son suficientes para determinar las reacciones.
Cuando el número de reacciones es superior a tres, tenemos una estructura hiperestática y es necesario considerar la rigidez de la misma para poder determinar completamente las reacciones.
En este último caso existen diversos métodos para determinarlas: Dado un sólido una condición necesaria para que este sólido esté en equilibrio mecánico es que la suma de reacciones y el momento resultante de estas reacciones sea cero:
{\displaystyle \sum _{i=1}^{n}{\vec {F}}_{i}=0,\qquad \sum _{i=1}^{n}{\vec {r}}_{i}\times {\vec {F}}_{i}+\sum _{j=1}^{m}{\vec {M}}_{j}=0,}
Si el sólido es indeformable la condición además de necesaria es suficiente, sin embargo, para ciertos sólidos deformables la condición de que la suma de fuerzas y momentos se anule puede no ser suficiente.
En ese último caso además deben satisfacerse locamente las ecuaciones diferenciales de equilibrio:
x y
x z
y x
y z
z y
{\displaystyle {\begin{cases}{\cfrac {\partial \sigma _{xx}}{\partial x}}+{\cfrac {\partial \sigma _{xy}}{\partial y}}+{\cfrac {\partial \sigma _{xz}}{\partial z}}+b_{x}=0\\{\cfrac {\partial \sigma _{yx}}{\partial x}}+{\cfrac {\partial \sigma _{yy}}{\partial y}}+{\cfrac {\partial \sigma _{yz}}{\partial z}}+b_{y}=0\\{\cfrac {\partial \sigma _{zx}}{\partial x}}+{\cfrac {\partial \sigma _{zy}}{\partial y}}+{\cfrac {\partial \sigma _{zz}}{\partial z}}+b_{z}=0\end{cases}}}
Donde: Las condiciones anteriores también son aplicables a un fluido y para la mayoría de fluidos admiten las ecuaciones anteriores son equivalentes a una forma más simple.